姿態控制中的散開現象

何朕,　王廣雄

(哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001)

?

姿態控制中的散開現象

何朕,王廣雄

(哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001)

摘要:對散開現象提出了一種新的解釋,并對姿態控制提出了一種新的PD型控制。實際應用中常用四元數來表示一剛體運動的姿態。可是四元數的狀態空間S3對姿態集合SO(3)是雙重覆疊的,即每一個姿態對應兩個不同的四元數向量。這樣,當采用四元數來進行反饋控制時,四元數的非唯一性會在q∈S3和-q∈S3的鄰域分別形成一個吸引域和一個排斥域,從而導致了姿態控制的散開現象。文中用一個姿態控制的實例來說明這個不穩定現象。為了避免出現散開現象,提出了一個PD型的非線性控制器。這種控制器還有一個特點是能夠以最小轉角來回歸平衡狀態。

關鍵詞:姿態控制; 四元數; 旋轉矩陣; 散開現象

王廣雄(1933—)，男，教授，研究方向為控制系統設計、魯棒控制及H∞控制等。

0引言

剛體運動的姿態常是通過幾個姿態參數來表示的。能表征姿態的最少的參數數是三個,但用三參數來表示姿態均存在奇異點[1]。所以一般是采用四元數來表示姿態。四元數是四個參數加一個約束方程。四元數具有全局性,可以表示所有的姿態,而且不存在奇異問題。可是四元數與姿態的關系卻不是唯一的。四元數狀態空間對于旋轉矩陣空間是雙重覆疊的,所以當用四元數來構成姿態的反饋控制時會出現姿態散開等不良的系統特性[1-2]。姿態散開以及避免散開的控制系統設計問題現在已成為姿態控制中的一個熱點問題[3-6]。不過多數文獻對于姿態散開問題都是基于S3和SO(3)空間之間的映射關系,從數學上作抽象的討論。本文則結合實際的例子分析,從物理概念上對姿態散開現象作出新的解釋,并在此基礎上提出解決方案。

1旋轉矩陣和四元數

飛行器、機器人、或空間的運動物體都有一個姿態控制問題。一個剛體的姿態是指剛體坐標的指向,是剛體坐標系對參考坐標系的一種相對轉動。這個轉動,即剛體的姿態是用一個姿態矩陣R來表示的。R陣的各列是剛體坐標系軸上的各單位向量在參考坐標系軸上的分量。設參考坐標系的三個正交的單位向量為i、j、k,轉動的剛體坐標系的三個正交的單位向量為i′、j′、k′,則R陣就是

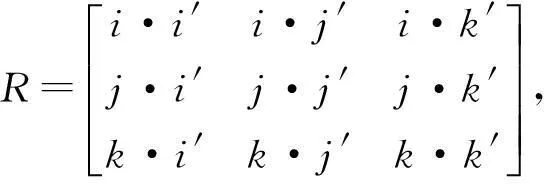
(1)

式中兩個單位向量的點乘就是向量之間夾角的余弦,例如

i·i′=cosα。

所以R陣也稱為方向余弦(矩)陣,有時也稱為旋轉矩陣。根據R陣的性質可知R陣的轉置等于R陣的逆,所以R陣的行列式等于1。這樣,由于行列式等的約束,雖然R陣有9個元素,各元素之間卻還存在著6個約束關系。這里將這個3×3的正交陣歸之為一類三階的特殊正交族(special orthogonal group),

SO(3)={R∈R3×3:RTR=RRT=I,detR=1}。

旋轉矩陣R可以全局,無奇異的來表示一個剛體的姿態,而且它所表示的姿態是唯一的。但是R陣有9個參數,而由于正交性對這些參數又加上了6個約束,所以不便于實際中使用。實際中常用參數化的方式來表示這個姿態矩陣R。不帶約束條件的能夠表示姿態的最少參數數目是三個,但三參數表示一般都存在奇異點。無奇異點的,能夠全局表示姿態的最少參數數目是四個,并帶一個約束式,這就是單位四元數(unitquaternion),簡稱四元數。

單位四元數定義為

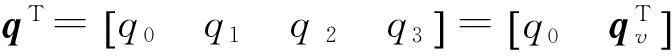
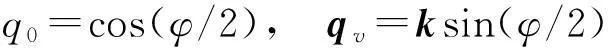
(2)

式中:φ是繞瞬時轉軸k的轉角,k為瞬時轉軸上的單位矢量,這里的約束條件是qTq=1。

旋轉矩陣R與四元數q的關系有Rodriques公式[3]

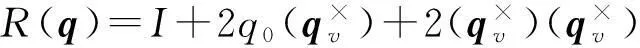
(3)

式中上角標×號表示向量積的矩陣表示,

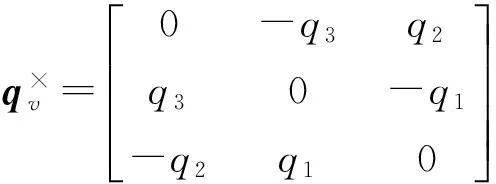
根據式(3)還可寫得

traceR=2cosφ+1。

故繞k軸的轉角φ為

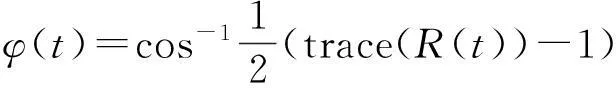
(4)

四元數的約束條件表明,這是一個R4空間中幅值等于1的向量的集合,稱為S3空間

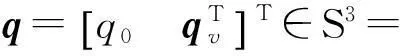
(5)

旋轉矩陣空間SO(3)表示的是一個有真實物理含義的姿態,而四元數空間S3則是姿態的一種參數化表示。這兩個空間是不一樣的。Rodrigues公式[式(3)]表示了S3→SO(3)的映射關系。從式(3)可見,對每個q∈S3來說,R(q)=R(-q),也就是說,每一個姿態對應兩個正相反的四元數向量。也可以說,四元數空間S3是雙重覆疊在SO(3)上的。姿態控制系統設計中,如果忽視了這種雙重性,系統就可能出現一些不良的性能,例如姿態的散開現象[1-2]。

2四元數姿態控制

現在具體結合一衛星的姿態機動控制來進行說明[7-8]。設衛星為剛體,其動力學方程為

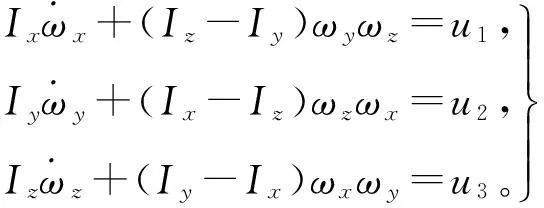
式中：Ix,Iy,Iz為相應軸的轉動慣量,ωx,ωy,ωz為繞相應軸的角速度分量,u1,u2,u3為相應軸的控制力矩。本例中設Ix=Iy=Iz=1kg·m2,故動力學方程為

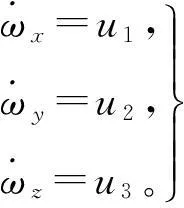
(6)

當姿態是用四元數來表示時,其相應的運動學方程為[9-10]

(7)

式中

本例中采用PD控制。當用四元數表示時,姿態控制采用PD控制已經從無源性的角度證明是穩定的[9-11]。PD控制律為

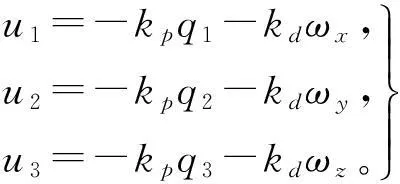
(8)

本例中取kp=0.1,kd=0.237。

為了簡化分析,這里設剛體在平衡點處繞x軸有一個初始運動(初始角度或角速度),現考察在PD控制下該姿態系統的調節過程。

由于只有x軸的轉動,所有剛體運動方程式只保留式(6)的第一項,即

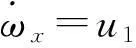
(9)

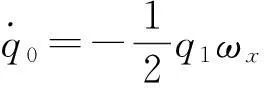
(10)

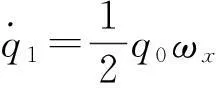
(11)

PD控制律為

u1=-kpq1-kdωx。

(12)

對式(11)求導,得

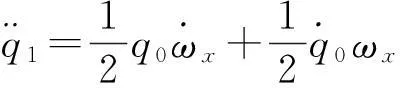
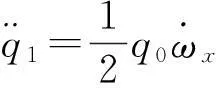
將式(9)(11)和(12)代入上式,得

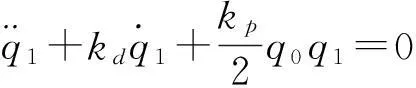
將本例中的kp和kd代入后得特征方程為

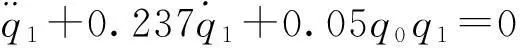
(13)

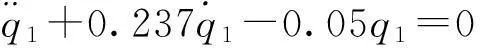
(14)

式(14)是個鞍奇點的特征方程,系統是不穩定的。

從上述分析可知,當采用四元數時,姿態控制系統會存在兩個平衡點,一個是穩定的,另一個是不穩定的,這兩個S3上的平衡點都對應于SO(3)空間上的同一個姿態。所以即使初始姿態離平衡點很近,但如果是處于不穩定的鞍奇點附近,這PD控制還會將姿態拉開平衡點,繞一個整圈進入到S3上穩定的平衡點才靜止下來,這就是姿態的散開(unwinding)現象。

3姿態控制中的散開現象

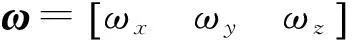
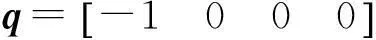
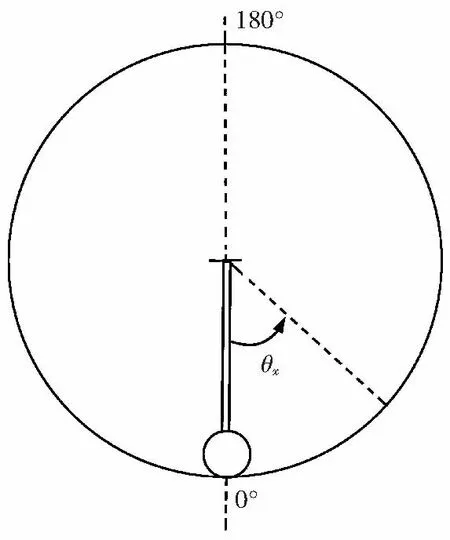
圖1　轉動的示意圖

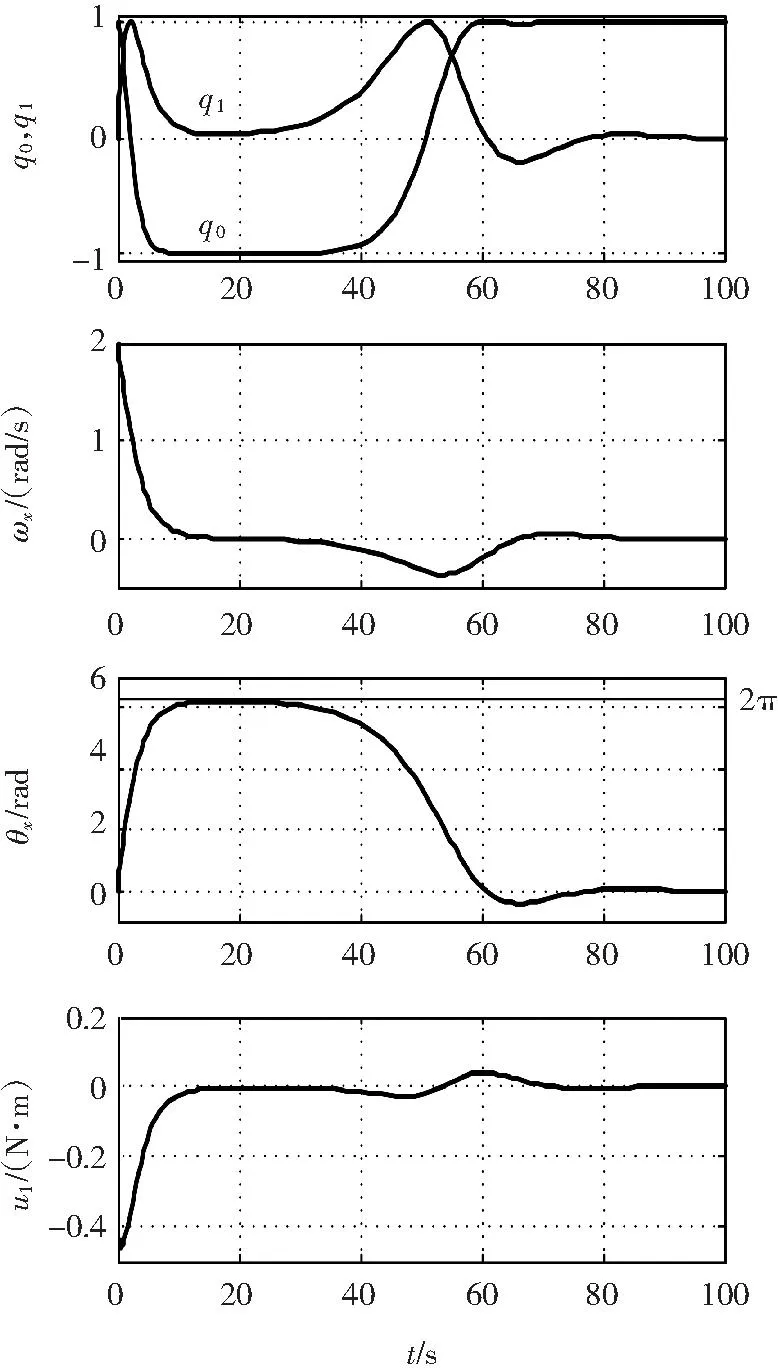
圖2　姿態的散開現象

散開現象的實質是因為反饋控制是根據q空間的上半球來設計的,當運動到q的下半球時,q已經改變了符號,所以負反饋變成了正反饋,系統就不穩定了。如果能隨著q進入下半球,反饋控制律也隨之改變,就能保證穩定了,即要求控制律u滿足

u(q,ω)=u(-q,ω) 。

(15)

對于PD控制來說,如果將控制律設計成

u=-kpqvsgn(q0)-kdω。

(16)

就能滿足式(15)的要求。注意這里的

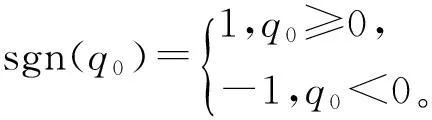
(17)

式(17)與Simulink中的符號模塊是不一樣的,使用時應該加以區分。圖3就是采用本文的控制律式(16)后同樣情況下的響應曲線。圖3表明在同樣的初始角速度ωx(0)=2 rad/s下,θx一圈以后(2π)就穩定下來了,系統穩定在q0=-1的平衡點上,不存在散開問題。

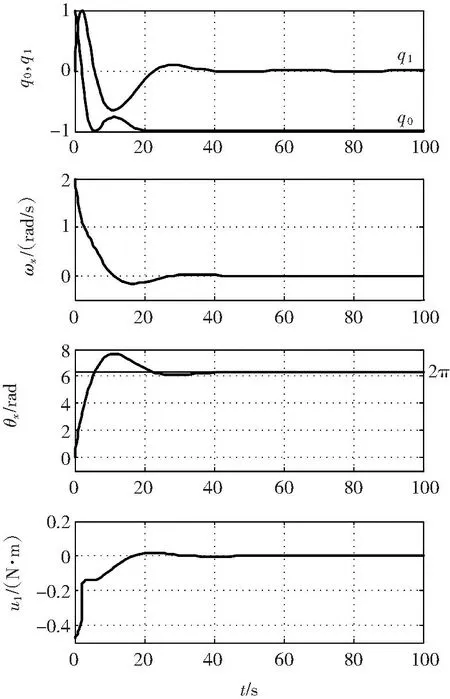
圖3　無散開現象的響應

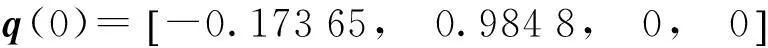
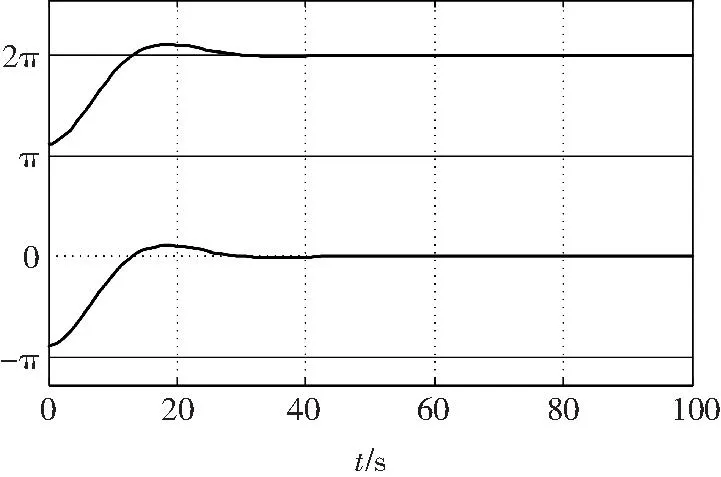
圖4　最小角度歸零

4結論

四元數空間S3與實際表示姿態的物理空間SO(3)是不一樣的。S3空間雙重覆疊在SO(3)上,因而出現了兩個不同性質的平衡點。如果忽視了四元素的這種雙重性,姿態控制系統會出現散開現象,即當初始條件接近平衡點時忽然會反方向繞開去,繞一整圈后再回到平衡點。因此當采用四元素時,要注意在姿態控制設計中避免姿態散開現象。文中提出的控制律是一種基本的PD型控制,更一般的控制律中由于要包含切換控制,所以歸屬于混雜系統。這種混雜系統再加上噪聲,是當前姿態控制的一個研究熱點[3-6],也是近期的一個研究方向。

參 考 文 獻:

[1]CHATURVEDI N A, SANYAL A K, MCCLAMROCH N H. Rigid-body attitude control[J]. IEEE Control Systems Magazine, 2011, 31(3): 30-51.

[2]BHAT S P, BERNSTEIN D S. A topological obstruction to continuous global stabilization of rotational motion and the unwinding phenomenon[J]. Systems and Control Letters, 2000,39(1): 63-70.

[3]MAYHEW C G, SANFELICE R G, TEEL A R. Quaternion-based hybrid control for robust global attitude tracking[J]. IEEE Trans Automatic Control, 2011, 56(11): 2555-2566.

[4]MAYHEW C G, SANFELICE R G, SHENG J, et al. Quaternion-based hybrid feedback for robust global attitude synchronoization[J]. IEEE Trans Automatic Control, 2012, 57(8): 2122-2127.

[5]MAYHEW C G, SANFELICE R G, TEEL A R. On quaternion-base attitude control and the unwinding phenomenon[C]//2011 American Control Conference, June 29-July 01, 2011, San Francisco, USA. 2011: 299-304.

[6]MAYHEW C G, SANFELICE R G, TEEL A R. On the non-robustness of inconsistent quaternion-based attitude control systems using memoryless path-lifting schemes[C]//2011 American Control Conference, June 29-July 01, 2011, San Francisco, USA. 2011: 1003-1008.

[7]何朕, 孟范偉, 王廣雄, 等. 衛星大角度姿態機動控制的SOS設計[J]. 中國空間科學技術, 2013, 33(5): 69-75.

HE Zhen, MENG Fanwei, WANG Guangxiong, et al. SOS design for control of large attitude maneuvers of satellites[J]. Chinese Space Science and Technology, 2013, 33(5): 69-75.

[8]何朕, 王廣雄, 孟范偉. 非線性H∞控制的SOS設計[J]. 電機與控制學報, 2015, 19(1): 82-89.

HE Zhen, WANG Guangxiong, MENG Fanwei. SOS design for nonlinear H∞control[J]. Electric Machines and Control, 2015, 19(1): 82-89.

[9]WEN J T, KREUTZ-DELGADO K. The attitude control problem[J]. IEEE Trans Automatic Control, 1991, 36(10): 1148-1162.

[10]LIZARRALDE F, WEN J T. Attitude control without angular velocity measurement: a passivity approach[J]. IEEE Trans Automatic Control, 1996, 41(3): 468-472.

[11]TSIOTRAS P. Further passivity results for the sttitude control problem[J]. IEEE Trans Automatic Control, 1998, 436(11): 1597-1600.

(編輯：張詩閣)

Unwinding phenomenon in attitude control

HE Zhen,WANG Guang-xiong

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Abstract:A new exposition of the unwinding phenomenon was presented and a new type of PD controller for attitude control was proposed. The quaternions are often used in practical applications to represent rigid-body attitude. However, the quaternion state space S3double covers the set of attitudes SO(3) in the sense that each attitude corresponds to two different quaternion vectors. Thus, in the case of feedback control using quaternions, this nonunique representation can give rise to regions of attraction and repulsion in the neighborhood of q∈S3and-q∈S3, respectively, and cause the unwinding phenomenon of attitude control. A practical attitude control example was presented to illustrate this unstable behavior. A PD-type nonlinear controller was proposed to avoid the unwinding phenomenon. This controller also has an advantage of retuning to the equilibrium state with minimum angle of rotation.

Key words:attitude control; quaternion; rotation matrix; unwinding phenomenon

通訊作者:何朕

作者簡介:何朕(1972—)，女，博士，教授，研究方向為控制系統設計、魯棒控制及H∞控制等；

基金項目：國家自然科學基金重點資助項目(61034001); 國家自然科學基金資助項目(61174203,60374027)

收稿日期:2014-09-16

中圖分類號:TP 273

文獻標志碼:A

文章編號:1007-449X(2015)07-0101-05

DOI:10.15938/j.emc.2015.07.015