第二型邊界條件下拋物型方程反問題的變分迭代解法

黃得建，李艷青

(瓊州學院 數學系，海南 三亞 572022)

?

第二型邊界條件下拋物型方程反問題的變分迭代解法

黃得建，李艷青

(瓊州學院 數學系，海南 三亞 572022)

應用變分迭代法研究了第二邊值條件下拋物型偏微分方程反問題的數值解法,得到拋物型偏微分方程反問題中的兩個未知參數和方程的精確解,并通過例子說明這種方法的有效性.

變分迭代法;反拋物型方程;第二型邊界條件;拉格朗日乘子;未知參數

0引言

考慮下面的一維拋物型方程[1]：

(1)

同時滿足在空間區域內一點處溫度的測量值

u(x*,t)=E(t),t∈(0,T]

(2)

和在邊界處溫度的測量值

u(1,t)=μ2(t),t∈(0,T],

(3)

其中：φ(x),μ1(t)和μ2(t)為初始和邊界條件,f(x,t),|E(t)|>0為已知函數,p(t),q(t)為未知函數;x*∈(0,1)是固定的一點,(2)式和(3)式稱為附加條件.

(1)-(2)式描述一些特定類型的數理方程[2-3],(2)式和(3)式分別表示在某一時刻t在x*處和x=1處測量的溫度分布函數,q(t)表示在x=0處的表面熱流量q(t). 模型(1)-(2)解的存在性和唯一性在文獻[4]已經被證明.

通過附加邊界條件來識別拋物型偏微分方程中的系數被稱為反系數問題,又稱之為拋物型方程反問題. 文獻[2-6]研究了半線性拋物型方程反系數問題,得到這類問題的一些性質,并通過一些數值解法得到這類問題的數值解.

1 變分迭代法

變分迭代法是何吉歡提出來的[7],這種方法被成功的應用到初值問題[8]、雙曲型偏微分方程[9]、強非線性方程[10]、分數階非線性方程[11]和廣義KdV方程[12]. 本文將應用變分迭代求出模型(1)- (3)的解和未知參數p(t)和q(t).

應用以下兩個變換[13],設

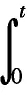
(4)

和

w(x,t)=u(x,t)r(t)，

(5)

則問題(1)-(3)能化為如下形式：

(6)

以及

(7)

由(4)式和(5)式可知

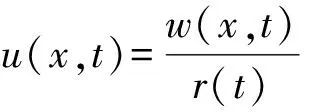
(8)

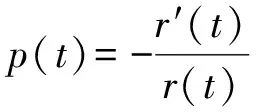
(9)

顯然,原問題(1)-(2)同輔助問題(6)-(7)是等價的. 文獻[2,3]已給出問題(6)-(7)解的存在性和唯一性.

根據變分迭代法，對(6)式中的第一個方程構造t-方向上的校正泛函如下形式

(10)

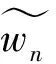
對(10)式兩邊變分,整理可得:

利用分步積分公式,可得

δwn+1(x,t)=δwn(x,t)+(1+λ(t))-?t0δwn(x,s)λ′(s)ds=0,

即

所以有

λ(t)=-1.

將λ(t)代入(10)式,可得到如下解的迭代公式：

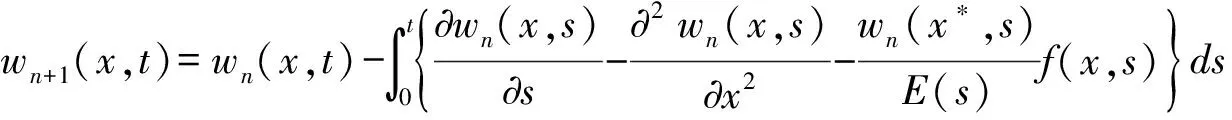
(11)

由(11)式可得到(6)式的解w(x,t),再由(8)式和(9)式可得原問題的解u(x,t)及未知參數p(t)和q(t).

2 實例

考慮模型(1)-(2),條件如下：

附加條件為：

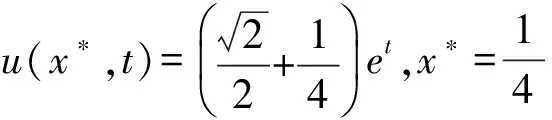
設

w0=cos(πx)+x,

由迭代公式(11)式可得：

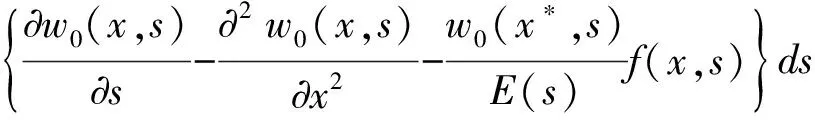
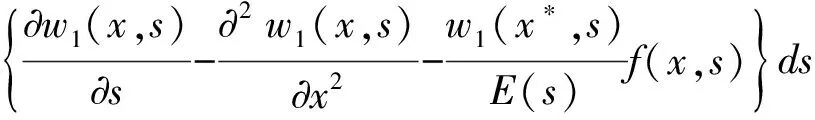
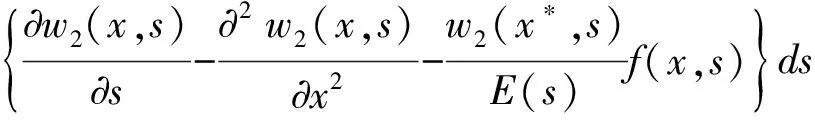
所以

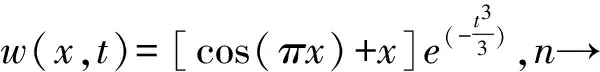
由(8)式和(9)式可得原問題的解

u(x,t)=[cos(πx)+x]et,p(t)=1+t2,q(t)=et.

文獻[1]中應用有限差分法也得到相同的解.

3 結論

本文成功的將變分迭代法運用于第二型邊界條件下拋物型方程反問題的求解,運用這種方法不需要分離變量,不需要計算復雜的隱式差分序列,方便使用數學軟件進行編程,不占用太多存儲空間,收斂速度也比較快,是一種非常方便使用的方法.

[1]李義軍. 拋物型方程反問題的數值解法研究[D].湖南:長沙理工大學, 2008 :10-16.

[2]Cannon J R, Lin Y, Wang S. Determination of a control parameter in a parabolic partial defferential equation[J].J Aust Math Socser B, 1991,33(2):149-163.

[3]Cannon J R, Lin Y, Xu S. Numerical procedures for the determination of an unknown coefficient in semi-linear parabolic defferential equations[J].Inverse Problem,1994(10):227-243.

[4]S.Wang, Y.Lin. A finite difference solution to an inverse problem determining a control function in a parabolic partial differential equation[J].Inverse Problem,1989(5):631-640.

[5]M. Tatari, M.Dehghan. He’s variational iteration method for computing a control parameter in a semi-linear parabolic equation[J].Chaos Solitons Fractals, 2007, 33(2):671-677.

[6]Can Baran Emine. Numerical procedures for determining of an unknown parameter in parabolic equation[J].Applied Mathematics and Computation, 2005, 16(2):1219-1226.

[7]J H.He. Variational iteration method-Some receant results and new interpretations[J].J Comput Appl Math,2007,207(1):3-17.

[8]Yongxiang Zhao, Aiguo Xiao. Variational iteration method for singular perturbation initial value problems[J].Computer Physics Communications, 2010,181:947-956.

[9]黃得建，李艷青. 雙曲型偏微分方程的變分迭代解法[J].瓊州學院學報,2013,20(2):1-3.

[10]JH.He. Some asymptotic methods for strongly nonlinear problems[J].Int.J.Mod.Phys, 2006,20:1141-1199.

[11]王文華，黃得建. 分數階微分-積分方程的迭代解法[J].瓊州學院學報,2010,17(2):1-3.

[12]H.Tari, D D.Ganji, M.Rostamian. Approximate solutions of K (2,2),KdV and modified KdV equations by variatiional iteration method, homotopy perturbation method and homotopy analysis method[J].Int.J.Nonlinear Sci., 2007, 8(2):203-210.

[13]Can Baran Emine. Numerical procedures for determining of an unknown parameter in parabolic equation[J].Applied Mathematics and Computation, 2005,162:1219-1226.

Variational Iteration Method for Solving an Inverse Problem of Parabolic Equation with Neumann Boundary Conditions

HUANG De-jian， LI Yan-qing

(Department of Mathematics, Qiongzhou University, Sanya Hainan, 572022，China)

In the current research, the variational iteration method was used to study the exact solution of an inverse parabolic problem with Neumann boundary conditions. Consequently, obtained are the exact solution and two unknown parameters of the parabolic partial difference equation . To show the efficiency of the present method, one interesting example is presented.

variational iteration method; inverse parabolic equation; Neumann boundary conditions; Lagrange multipliers; unknown parameter.

2015-09-30

瓊州學院青年教師科研基金項目(QYQN201519);瓊州學院青年教師科研基金項目(QYQN201520)

黃得建(1980-)，男，河南太康人，瓊州學院數學系講師，碩士，研究方向為偏微分方程的數值解.

李艷青(1978-)，女，河南武陟人，瓊州學院數學系講師，碩士，研究方向為奇點理論及應用，偏微分方程.

O241

A

1008-6722(2015) 05-0013-04

10.13307/j.issn.1008-6722．2015．05．04