離心力影響下的高速主軸-拉桿系統(tǒng)動態(tài)特性

李特,芮執(zhí)元,雷春麗,胡赤兵,劉軍

(1.蘭州理工大學數(shù)字制造技術(shù)與應用省部共建教育部重點實驗室,730050,蘭州; 2.蘭州理工大學機電工程學院,730050,蘭州)

?

離心力影響下的高速主軸-拉桿系統(tǒng)動態(tài)特性

李特1,2,芮執(zhí)元1,2,雷春麗1,2,胡赤兵1,2,劉軍1,2

(1.蘭州理工大學數(shù)字制造技術(shù)與應用省部共建教育部重點實驗室,730050,蘭州; 2.蘭州理工大學機電工程學院,730050,蘭州)

為進一步明確離心力對主軸系統(tǒng)動態(tài)特性的影響,以高速主軸-拉桿系統(tǒng)為對象,建立了刀柄的接觸力學模型,考慮了碟簧在離心力作用下產(chǎn)生的徑向伸展,并計算了該變形導致的拉力隨主軸轉(zhuǎn)速的變化關(guān)系。在此基礎(chǔ)上,討論了刀柄接觸應力隨初始拉力、動態(tài)夾緊力的變化規(guī)律,揭示了上述變化對主軸系統(tǒng)自然頻率的影響。結(jié)果表明:碟簧的徑向伸展會造成刀桿拉力的減小,但減小的程度受碟簧規(guī)格和初始拉力的影響,對于拉緊力較小的超高速主軸,該影響較為顯著,而對于拉緊力較大的普通主軸,該影響可以忽略;靜、動態(tài)夾緊力的夾緊效率隨摩擦因數(shù)的增大而降低;動態(tài)夾緊力可顯著提升接觸應力,但過高的夾緊力反而會加大接觸間隙,降低結(jié)合部阻尼,導致主軸系統(tǒng)自然頻率的減小。

高速主軸;拉桿;離心力;碟簧;接觸應力;自然頻率

切削技術(shù)的快速發(fā)展要求主軸在具有較高轉(zhuǎn)速的同時具有高剛性,以抵抗受迫振動,避免切削顫振。主軸系統(tǒng)的剛度不僅取決于各部件的剛度,更依賴于各結(jié)合部的剛度特性。對加工中心而言,影響主軸系統(tǒng)剛度的兩大因素分別為主軸-軸承系統(tǒng)和拉桿系統(tǒng)[1]。主軸-軸承系統(tǒng)的剛度由軸承類型、布置形式、預緊力和過盈量等因素決定,而拉桿結(jié)構(gòu)的剛度則取決于初始拉力和主軸-刀柄、刀柄-刀具結(jié)合面的剛度。在高轉(zhuǎn)速下,主軸-軸承與主軸-刀柄的聯(lián)結(jié)狀態(tài)都會因各自的離心膨脹而變化,造成結(jié)合部剛度的改變,從而影響總剛度。目前,多數(shù)文獻著重研究主軸-軸承系統(tǒng)的動、熱特性,并以高速時離心力作用下軸承的“剛度軟化”和摩擦生熱為代表,取得了一系列豐碩成果。刀柄系統(tǒng)的研究主要包括對主軸-刀柄結(jié)合部的動力學建模和因離心膨脹所造成的結(jié)合部“剛度軟化”效應的分析,前者以彈簧-阻尼單元模擬結(jié)合部的剛度特性,但建模多基于靜態(tài)而忽略了主軸轉(zhuǎn)動引起的“剛度軟化”效應,后者主要分析高主軸轉(zhuǎn)速下結(jié)合部的接觸特性,如主軸和刀柄的離心膨脹對接觸應力及結(jié)合面接觸率的影響,以及確定剛度喪失時的“臨界轉(zhuǎn)速”,研究通常以SK刀柄或HSK刀柄為對象。傳統(tǒng)7/24錐度的SK刀柄由于高速時過大的徑向膨脹使得接觸剛度下降過快,而HSK刀柄則克服了這一缺點,并因其獨有的兩面定位和高夾緊效率而被廣泛應用。張松等利用有限元技術(shù)分析了離心力對結(jié)合部接觸應力分布規(guī)律的影響[2];王貴成等深入研究了HSK刀柄的剛度特性和抗彎能力[3];張國軍等建立了基于HSK刀柄的臨界轉(zhuǎn)速模型和可靠性模型,分析了夾緊力和過盈量對二者的影響,并得到了可靠度隨主軸轉(zhuǎn)速的變化規(guī)律[4]。但是,多數(shù)文獻只考慮了主軸和錐面的徑向膨脹,而忽略了夾爪所產(chǎn)生的動態(tài)夾緊力對刀柄接觸特性的影響,更沒有考慮該夾緊力和拉桿拉力對整個拉桿系統(tǒng)動態(tài)特性及主軸系統(tǒng)的影響。Jiang等指出,隨著主軸轉(zhuǎn)速的提高,只對主軸-軸承系統(tǒng)建模已經(jīng)不能滿足高精度的要求,而考慮拉桿系統(tǒng)的雙轉(zhuǎn)子模型則能較好地預測主軸系統(tǒng)的動力學特性[5]。以往的設(shè)計和研究通常認為拉桿的初始拉力是恒定的,未考慮動態(tài)效應和離心力的影響,而拉力是由碟簧形變產(chǎn)生的,主軸高速旋轉(zhuǎn)時的離心力不僅會使主軸和刀柄膨脹,還會引起碟簧的軸向壓縮和徑向伸展,因此初始拉力也會隨之改變。文獻[1]中分析了離心力對拉桿系統(tǒng)拉力的影響,發(fā)現(xiàn)隨著主軸轉(zhuǎn)速升高,離心力的增大會造成動態(tài)拉力的下降,從而影響到刀柄的夾持效率,并推測夾緊效率受到摩擦力的顯著影響;文獻[6]討論了某型號主軸拉桿的拉力在離心力作用下的變化,指出該變化是由碟簧的徑向伸展引起的。拉力的改變不僅會影響動、靜態(tài)夾緊力,改變刀柄結(jié)合面的接觸特性[7],還會使主軸頻率發(fā)生變化[8],從而對主軸的整體動態(tài)特性產(chǎn)生不可忽略的影響。因此,有必要在考慮拉力變化的基礎(chǔ)上分析刀柄結(jié)合部的接觸特性和刀桿系統(tǒng)的動力學特性,以及這2種特性的變化對主軸整體性能造成的影響。

本文從拉桿系統(tǒng)的結(jié)構(gòu)出發(fā),以HSK A63刀柄系統(tǒng)為研究對象,建立了考慮動態(tài)夾緊力的主軸-刀柄接觸力學模型和主軸-刀桿三維實體模型,以主軸高速旋轉(zhuǎn)時的離心力為誘因,研究了碟簧徑向伸展引起的拉緊力減小現(xiàn)象和動態(tài)夾緊力影響下的刀柄-主軸接觸特性,以及這些因素影響下的主軸整體動態(tài)特性,旨在完善主軸系統(tǒng)的動態(tài)特性研究。

1 離心力作用下的旋轉(zhuǎn)部件力學模型

1.1 主軸-刀柄裝配關(guān)系

圖1所示為主軸-HSK A63刀柄裝配關(guān)系示意圖,左端顯示了主軸-刀柄的連接,其上、下兩半部分分別為未拉緊與拉緊時的狀態(tài)。拉桿的拉力由碟簧變形產(chǎn)生,刀柄與主軸采用膨脹式夾緊機構(gòu)連接,拉桿受力向右移動時會帶動夾爪張開,夾爪楔面與刀柄孔的30°錐面相接觸,同時刀柄端面與主軸端面貼緊,從而實現(xiàn)兩面定位與夾緊。

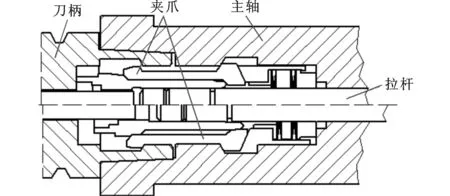
圖1 主軸-HSK A63刀柄裝配示意圖

1.2 碟簧的靜彈性變形與離心變形

碟簧的變形和拉力的改變會影響主軸-刀柄結(jié)合部的剛度和切削性能,因此在高速精密主軸的設(shè)計和加工中應考慮這部分變化[6]。圖2為碟簧示意圖。

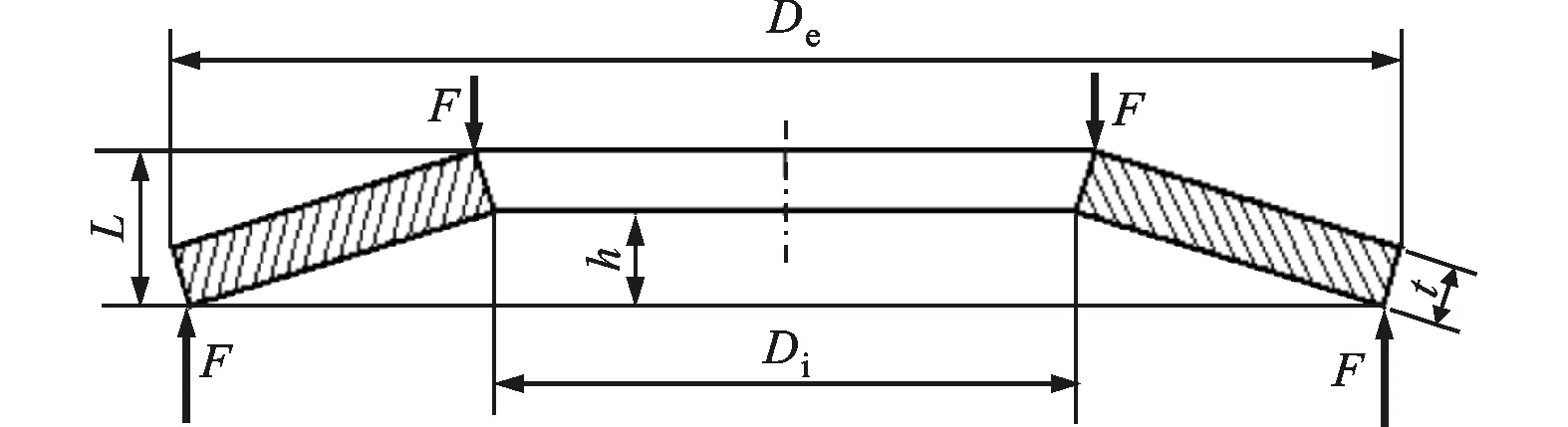
圖2 碟簧示意圖

Almen和Laszlo建立了靜態(tài)時碟簧變形量δ與彈力Q的關(guān)系式[9]

(1)

式中:E為彈性模量;ν為泊松比;h為未變形時的自由高度;t為碟簧厚度;

(2)

(3)

(4)

r2和r2分別為碟簧的內(nèi)圈半徑和外圈半徑。若碟簧材料為50CrVA,則相應的參數(shù)為E=2.06 GPa,ν=0.3,ρ=7.86 g/cm3。Almen等通過試驗證明,Q-δ關(guān)系式在不考慮摩擦的情況下能較好地反映碟簧的變形與彈力關(guān)系。此外,眾多學者已證明,有限元模型也可以精確模擬碟簧的上述關(guān)系[6,10]。Bagavathiperumal等在考慮幾何非線性的基礎(chǔ)上以有限元法模擬了碟簧的彈性變形,模擬結(jié)果與試驗及理論結(jié)果非常接近[10],說明有限元軟件能精確模擬碟簧的靜、動態(tài)性能。圖3為式(1)的計算結(jié)果與有限元模擬結(jié)果的比較,可見二者非常接近,當變形量為0.25 mm時,彈力值僅相差7.7%。因此,本文也利用有限元模型來分析碟簧受離心力作用時的變形及其與彈力的關(guān)系。

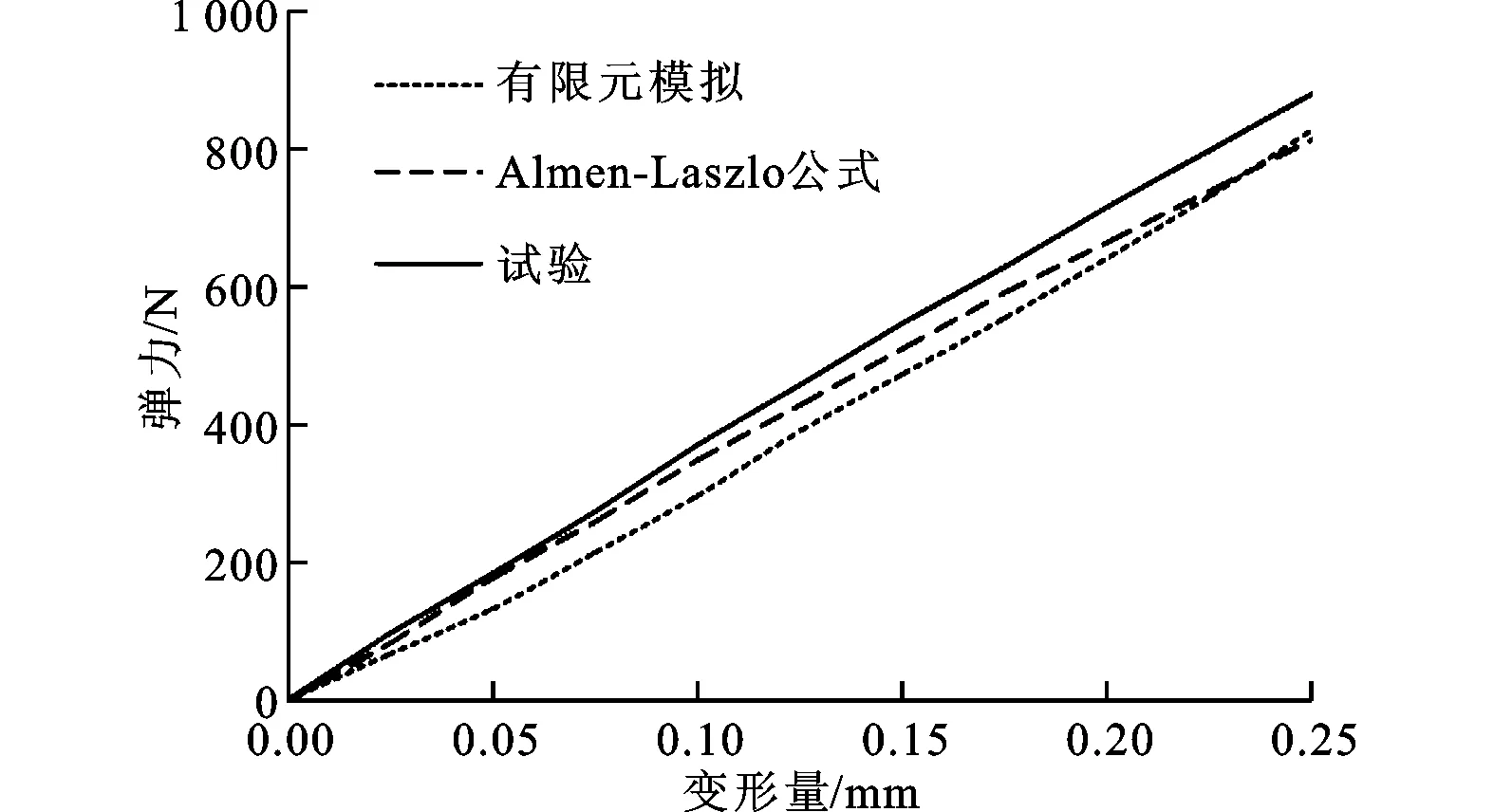
圖3 碟簧變形量與彈力的關(guān)系[6]

1.3 夾爪的靜、動態(tài)夾緊力

高速加工時HSK刀柄的受力狀況如圖4所示,所受到的夾緊力來自兩部分:一部分為初始夾緊力,由碟簧變形產(chǎn)生的拉力引起;另一部分由離心力引起,為動態(tài)力。

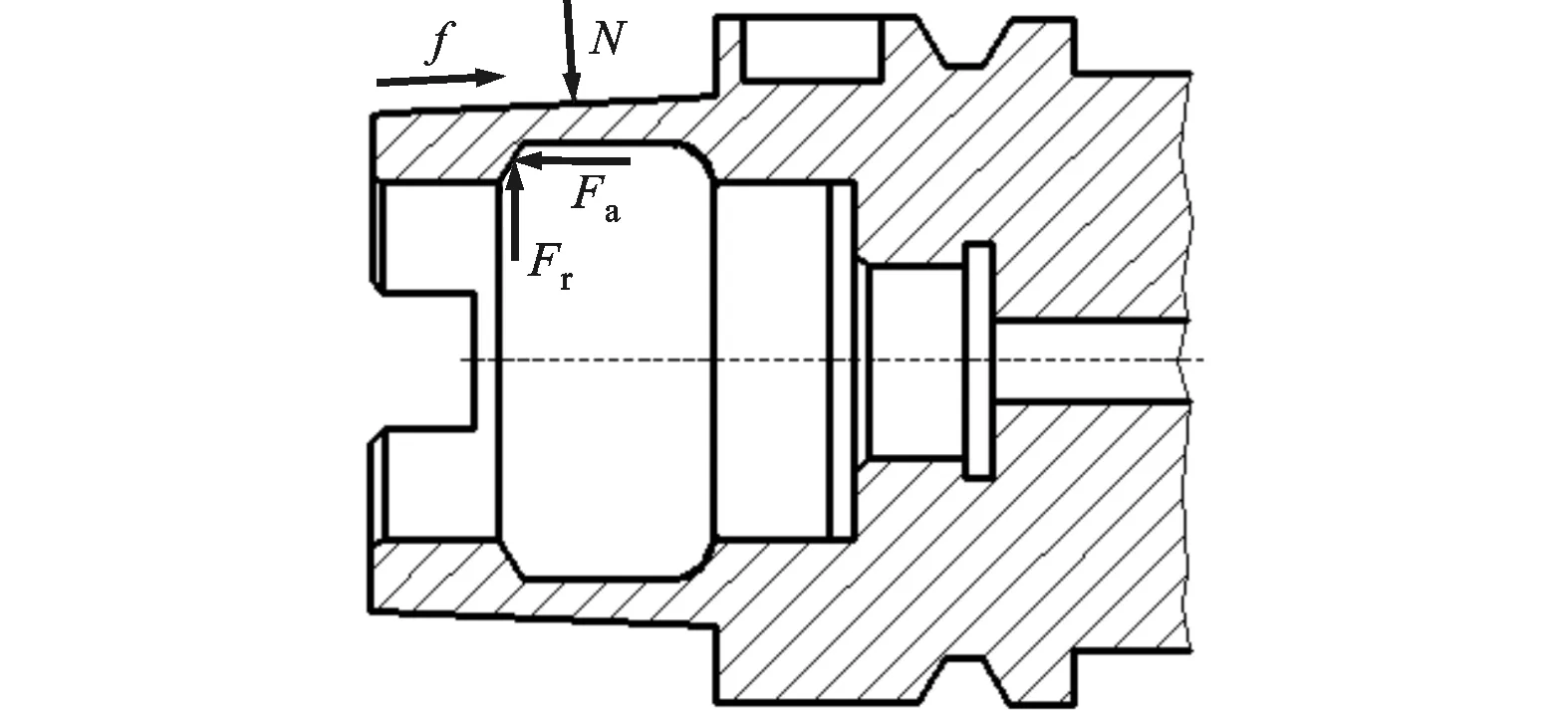
圖4 刀柄受力示意圖

文獻[11]推導了初始拉緊力F0與靜、動態(tài)夾緊力N2、Nc的關(guān)系,認為N2=1.29F0,Nc=Fc/2sinα(Fc為夾爪所受的離心力),然而卻忽略了結(jié)合面間的摩擦效應。考慮摩擦作用的靜、動態(tài)夾緊力可分別表示為[12]:

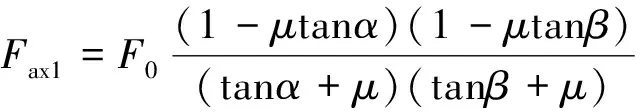
(5)

(6)

(7)

Frad2=Fc=mrω2

(8)

總夾緊力Fa=Fax1+Fax2

(9)

Fr=Frad1+Frad2

(10)

以上各式中:α為拉桿椎體的楔角;β為夾爪斜面的楔角;r為夾爪到旋轉(zhuǎn)中心的距離;m為夾爪的質(zhì)量;ω為旋轉(zhuǎn)角速度;μ為夾爪楔面與內(nèi)夾緊面間的摩擦因數(shù)。由1.2節(jié)可知,高速旋轉(zhuǎn)時初始夾緊力會因碟簧的伸展而改變,不再是常量,故可將F0記為F0(δ0),δ0為碟簧離心變形量。因此,夾緊力的變化由初始拉力的改變和動態(tài)夾緊力的改變兩方面引起。由式(8)可知,動態(tài)夾緊力與主軸轉(zhuǎn)速成二次方關(guān)系,主軸轉(zhuǎn)速越高,動、靜態(tài)夾緊力之比就越大。

1.4 主軸-刀柄結(jié)合面的接觸應力模型

因刀柄和主軸結(jié)合部的錐度很小,可將二者視為兩個空心圓盤,根據(jù)彈性力學理論可知,當二者回轉(zhuǎn)時,外圓盤的徑向膨脹量總是大于內(nèi)圓盤的膨脹量,因此需要預加過盈量和初始夾緊力以保證二者的良好接觸。于是,接觸應力同樣也由兩部分組成:一部分由實際過盈量產(chǎn)生,另一部分由夾爪的實際夾緊力產(chǎn)生。

1.4.1 過盈量產(chǎn)生的接觸應力 實際過盈量產(chǎn)生的接觸應力可按軸對稱平面應力問題求解,可以表示為[13]

(11)

式中:ρ為材料的密度;ν為泊松比;Δ為初始過盈量;a、b、c分別為刀柄內(nèi)、外徑和主軸外徑。

1.4.2 實際夾緊力產(chǎn)生的接觸應力 文獻[4]推導了實際夾緊力和接觸應力的關(guān)系,但是忽略了楔形面間的摩擦力,有可能導致結(jié)果不準確。由動態(tài)夾緊力導致的接觸面正壓力為[4]

N=Fasin2.87°+Frcos2.87°-0.75F0sin2.87°

(12)

根據(jù)圣維南原理,正壓力N可等價為刀柄外錐面所受的均布分力,因此將式(9)、式(10)代入式(12),可得

N={[0.05(1-μtanβ)+(tanβ+μ)][F0(1-

μtanα)+Fc(tanα+μ)]}/[(tanα+μ)(tanβ+

μ)]-0.038F0

(13)

(14)

A=π(R1+R2)l

(15)

以上各式中:A為刀柄外錐面面積;R1、R2分別為刀柄大、小端半徑。因此,總接觸應力為兩項應力之和,即

P=P1+P2

(16)

2 動力學分析

2.1 碟簧在離心力作用下的變形與拉力

由1.2節(jié)的分析可知,離心力的存在會使得碟簧徑向伸展,從而導致軸向變形量進一步增大,但是該變形在實際加工中卻難以測量,因此有限元成為了重要的分析手段。為說明該變形程度的大小,分別模擬0～50 000r/min范圍內(nèi)單個碟簧和成組復合碟簧的變形量及其對應的拉力變化,設(shè)置主軸轉(zhuǎn)速作為唯一邊界條件,材料性能與1.2節(jié)中的相同。圖5a所示為單個碟簧變形量隨主軸轉(zhuǎn)速的變化關(guān)系,可見隨著主軸轉(zhuǎn)速的升高,碟簧變形增加,在50 000r/min時變形量為5.39μm,拉力相應下降了1.7%,如圖5b所示。

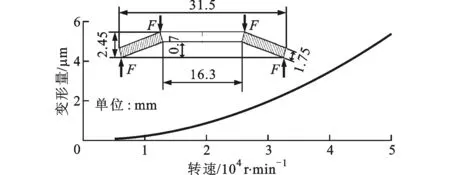
(a)碟簧變形量隨主軸轉(zhuǎn)速的變化

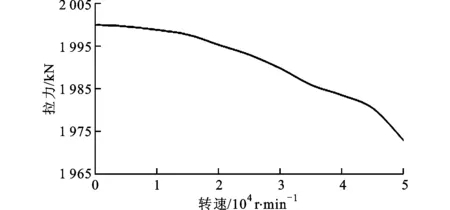
(b)拉力隨主軸轉(zhuǎn)速的變化圖5 碟簧變形量和拉力隨主軸轉(zhuǎn)速的變化關(guān)系

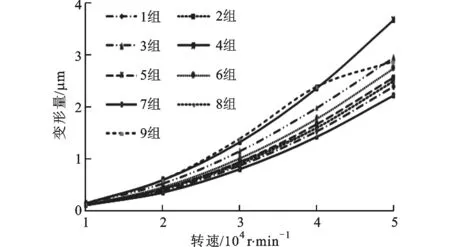
圖6 9組復合碟簧變形量比較

拉桿拉力通常由數(shù)片或數(shù)十片組合碟簧的變形產(chǎn)生。忽略摩擦,分別對組合數(shù)目從2至18的9組復合碟簧進行分析,結(jié)果表明:碟簧變形隨主軸轉(zhuǎn)速的上升而增大;在同一主軸轉(zhuǎn)速下,變形隨組合數(shù)目的增加變化緩慢,且以兩端變形最大,而中間部分變形較小,這可能是由于內(nèi)部各碟簧相互作用的結(jié)果。由圖6可見,除第4組外,其他幾組的最大變形量相差不大,都處于2～3μm區(qū)間,而HSKA63刀柄所需拉緊力至少為18kN,因此主軸轉(zhuǎn)速為50 000r/min時碟簧變形引起的拉力減小量小于等于0.1%,可見對于該主軸結(jié)構(gòu),由碟簧變形引起的拉力減小并非是影響其刀柄接觸特性的主要因素。

碟簧的變形程度受其規(guī)格及摩擦因數(shù)等多種因素制約,圖7所示為同種材料(50CrV4)的復合碟簧(6片)在不同摩擦因數(shù)和規(guī)格影響下的變形規(guī)律。由圖7a可見,摩擦因數(shù)對碟簧離心變形的影響較微弱,這與文獻[14]的研究結(jié)果一致,因此可忽略摩擦因素的影響。對比圖7b中的2條曲線可以發(fā)現(xiàn),若忽略厚度的影響,大直徑碟簧在同一主軸轉(zhuǎn)速下的變形量大于小直徑碟簧的變形量,可見碟簧變形還與其規(guī)格有關(guān)。結(jié)合圖6、圖7可以看出,當主軸轉(zhuǎn)速高于20 000r/min時,碟簧變形速率加快,但不同刀柄所需的拉力各異,致使相對變形率差異較大,因此,雖然大規(guī)格碟簧的變形程度更大,但與更高的拉力相比,該變形引起的拉力減小現(xiàn)象并不顯著。由此可知,主軸轉(zhuǎn)速是決定碟簧變形和拉力減小的最主要因素。文獻[6]表明,對于某型號的PCB鉆孔主軸,當轉(zhuǎn)速為300 000r/min時碟簧產(chǎn)生的拉力減小量占總拉力的4%。與本文的結(jié)論對比可知:碟簧變形引起的拉力減小現(xiàn)象對于以超高速為主的鉆削主軸更為明顯,值得重視,而對主軸轉(zhuǎn)速較低的銑削主軸的影響則不明顯。

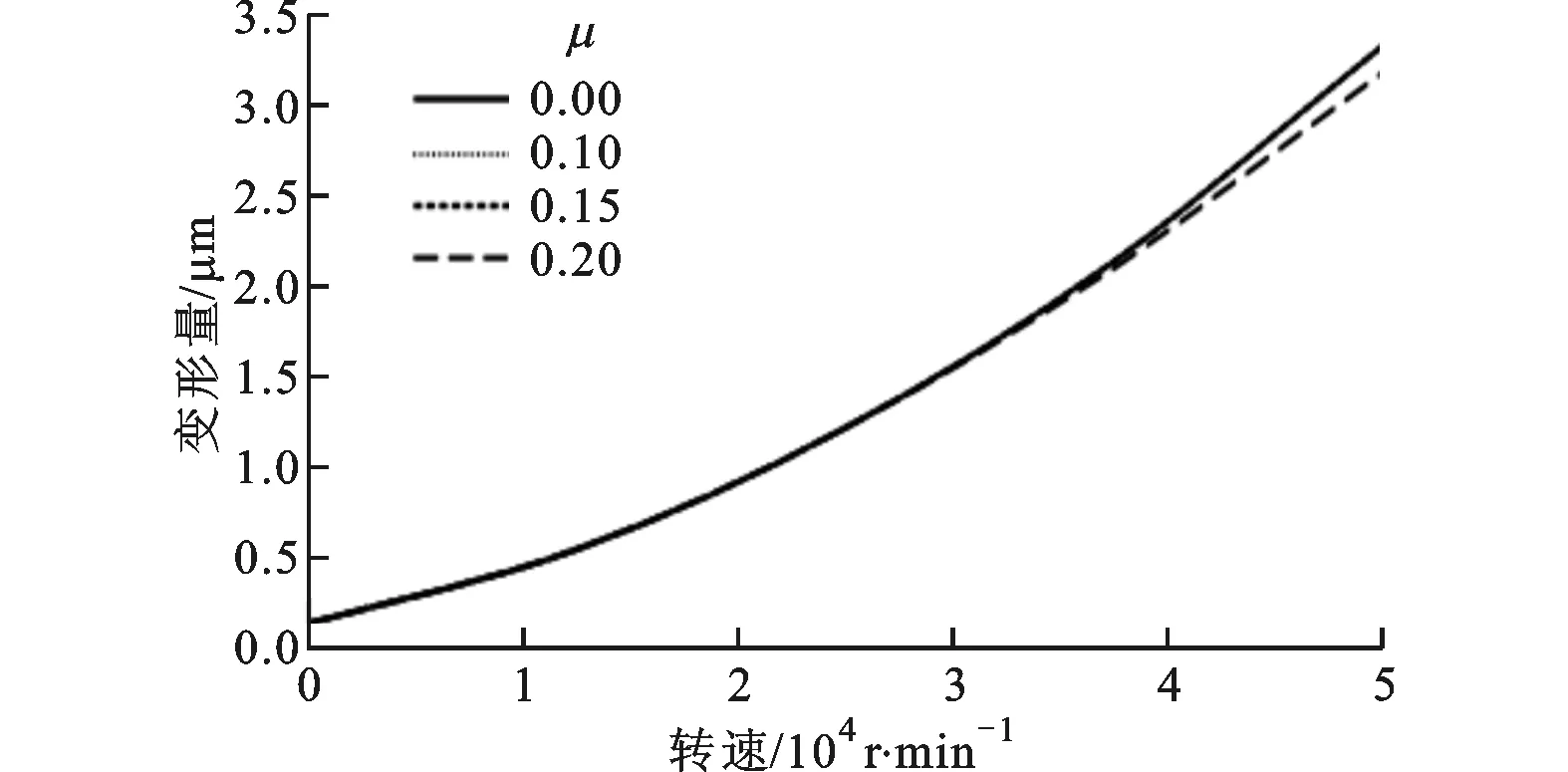
(a)考慮不同摩擦因數(shù)的碟簧變形曲線

(b)不同規(guī)格碟簧隨主軸轉(zhuǎn)速的變形曲線圖7 多種因素作用下碟簧的變形關(guān)系

2.2 動、靜態(tài)夾緊力

對于HSKA63型刀柄,其夾爪質(zhì)量m=153.3 g,到轉(zhuǎn)軸的距離r=14.56 mm,楔角β=30°[11]。將這些參數(shù)值代入式(7)、式(8)可得徑向及軸向的動態(tài)夾緊力,如圖8所示。從圖中可見,動態(tài)夾緊力與主軸轉(zhuǎn)速呈二次方關(guān)系,但摩擦狀況對軸向力影響顯著,同一主軸轉(zhuǎn)速下軸向動態(tài)力隨摩擦因數(shù)的增大呈減小趨勢。

(a)徑向動態(tài)夾緊力隨主軸轉(zhuǎn)速的變化

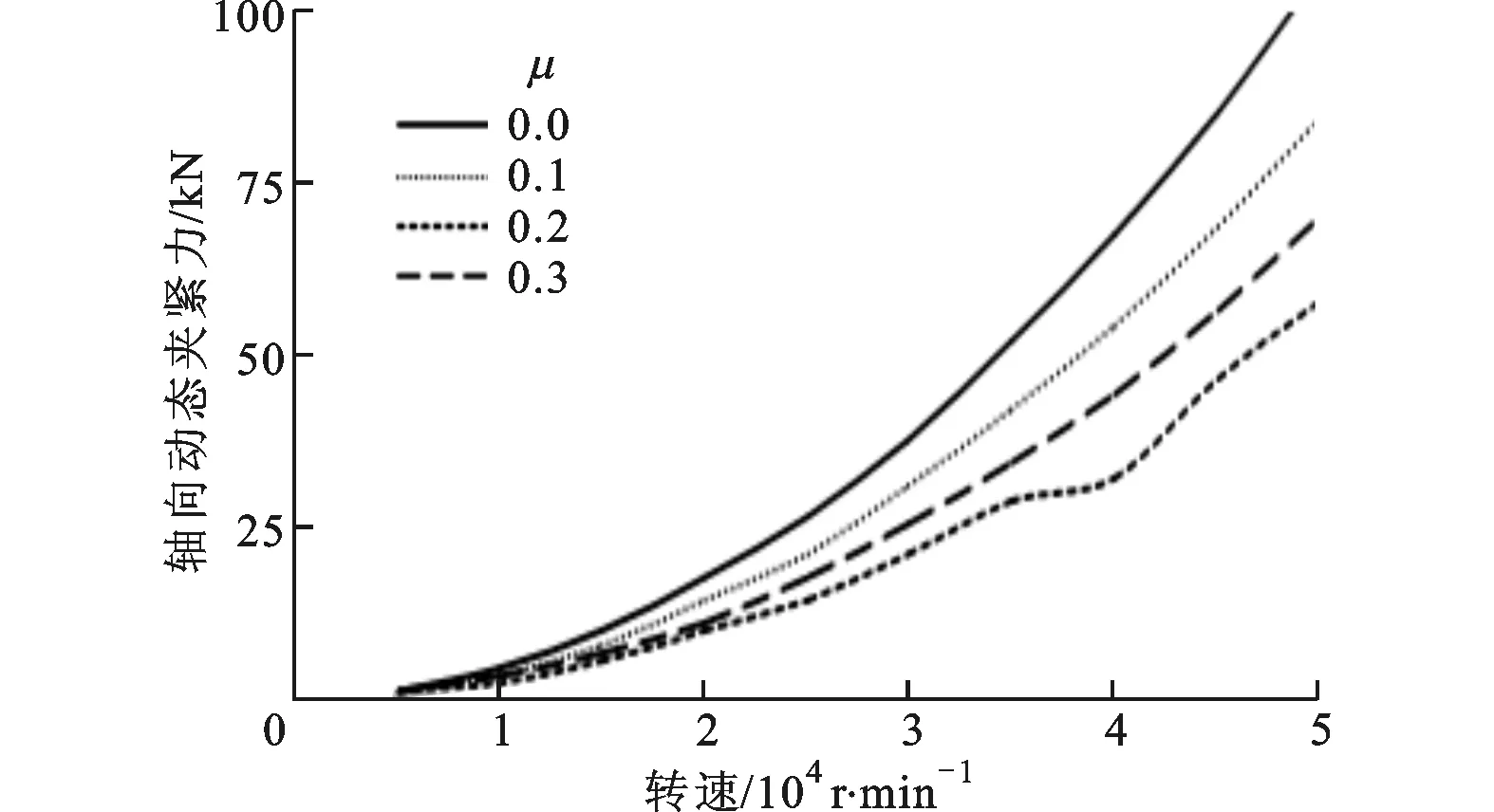
(b)不同摩擦因數(shù)下軸向動態(tài)夾緊力隨主軸轉(zhuǎn)速的變化圖8 動態(tài)夾緊力隨主軸轉(zhuǎn)速的變化關(guān)系

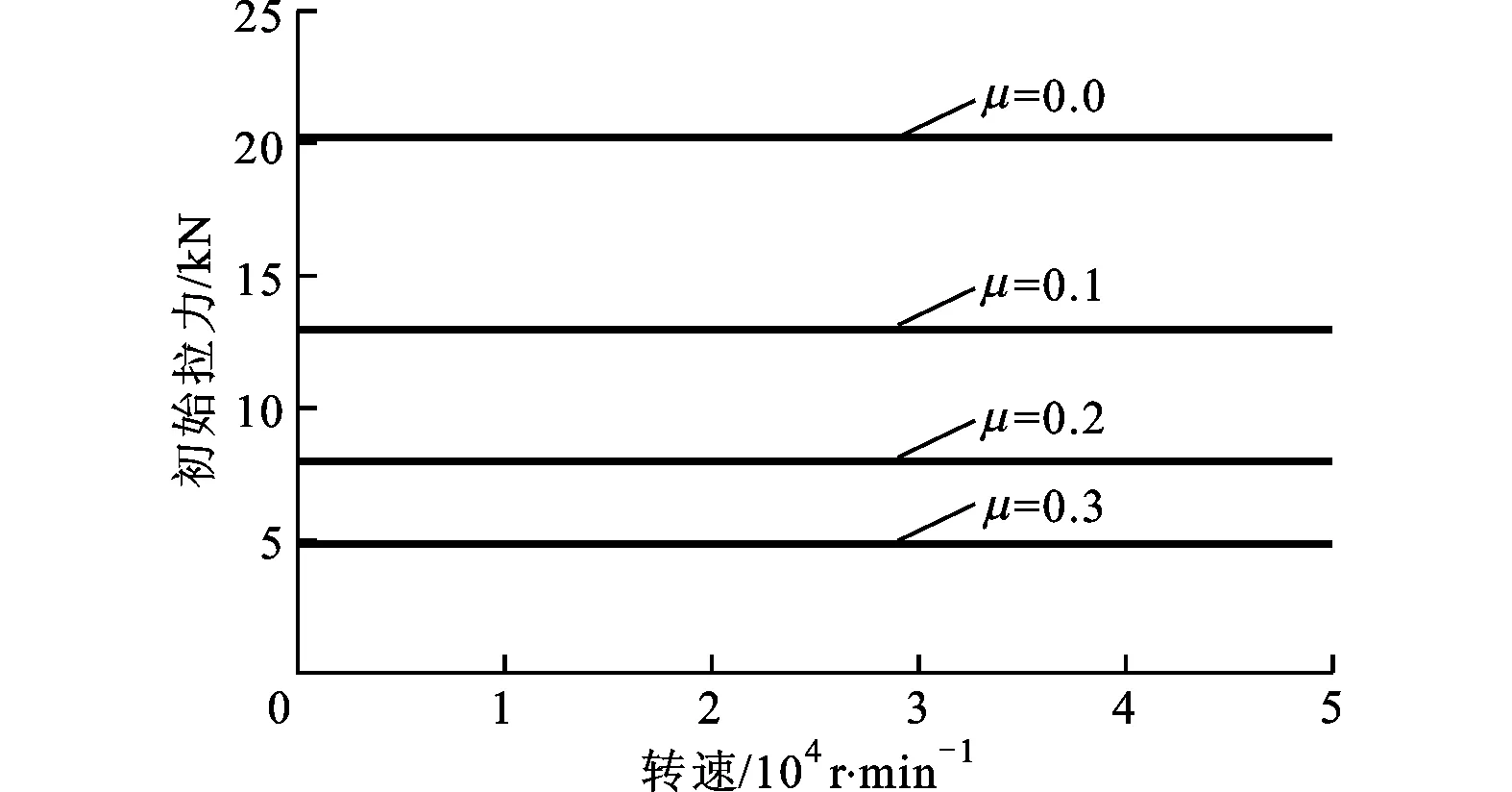
圖9 初始拉力隨主軸轉(zhuǎn)速的變化關(guān)系

由上述分析可知,碟簧的徑向伸展使得初始拉力F0也為變量,其隨主軸轉(zhuǎn)速的變化關(guān)系如圖9所示。從圖中可以看出,對于HSK A63刀柄,0.1%的拉力減小量雖不會影響靜拉力的改變,但該力的大小卻受摩擦因數(shù)的強烈影響,隨摩擦因數(shù)增大,靜態(tài)夾緊力下降,拉緊效率急劇下降。在不改變楔角的前提下,要提高靜態(tài)夾緊力,需提高楔面加工精度以達到減小摩擦因數(shù)的效果。比較動、靜態(tài)夾緊力的變化規(guī)律可知,雖然靜態(tài)夾緊力也隨主軸轉(zhuǎn)速下降,但其下降程度與動態(tài)夾緊力相比過小,對結(jié)合部接觸應力的影響可以忽略。通過以上分析可以得到如下結(jié)論:相對于超高速主軸,普通高速電主軸的初始拉力隨主軸轉(zhuǎn)速變化不明顯,對結(jié)合部接觸狀況影響不大,而超高速電主軸在設(shè)計和使用階段則需要考慮該變化所引起的結(jié)合部剛度下降現(xiàn)象。夾緊力減小不僅降低結(jié)合部的接觸剛度,還會造成切削點偏移,對于使用電主軸的滾齒機床,則會導致竄刀量的改變,引起齒廓誤差和刀具的不均勻磨損。

2.3 接觸間隙和接觸應力分布

接觸間隙和接觸應力是刀柄連接性能好壞的標志,過大的間隙和接觸應力會降低結(jié)合面可靠性,削弱加工精度,還會造成刀柄的破壞,因此有必要研究不同參數(shù)下間隙和應力的大小及分布。

2.3.1 靜拉力作用下的接觸間隙和接觸應力分布為能更真實地模擬夾爪對夾緊效果的影響,需建立包含夾爪的三維實體模型。建模時忽略內(nèi)孔、鍵槽等幾何特征,因刀柄為軸對稱回轉(zhuǎn)體,故可只建立1/2模型以減小體積并提升計算速度。所建模型如圖10所示。分別建立夾爪與刀柄內(nèi)孔30°斜面、主軸內(nèi)楔面以及刀柄和主軸間的接觸對,約束主軸右端面,在夾爪端面施加軸向力,由此得到靜拉力模型;去除軸向力,為回轉(zhuǎn)體施加轉(zhuǎn)速,即得到夾爪離心力作用下的動態(tài)夾緊模型。同時,需對該1/2模型做對稱處理。各部件材料參數(shù)為:密度ρ=7.86 g/cm3,彈性模量E=2.06 GPa,泊松比ν=0.3,結(jié)合面摩擦因數(shù)μ=0.15。

圖10 刀柄的1/2三維模型

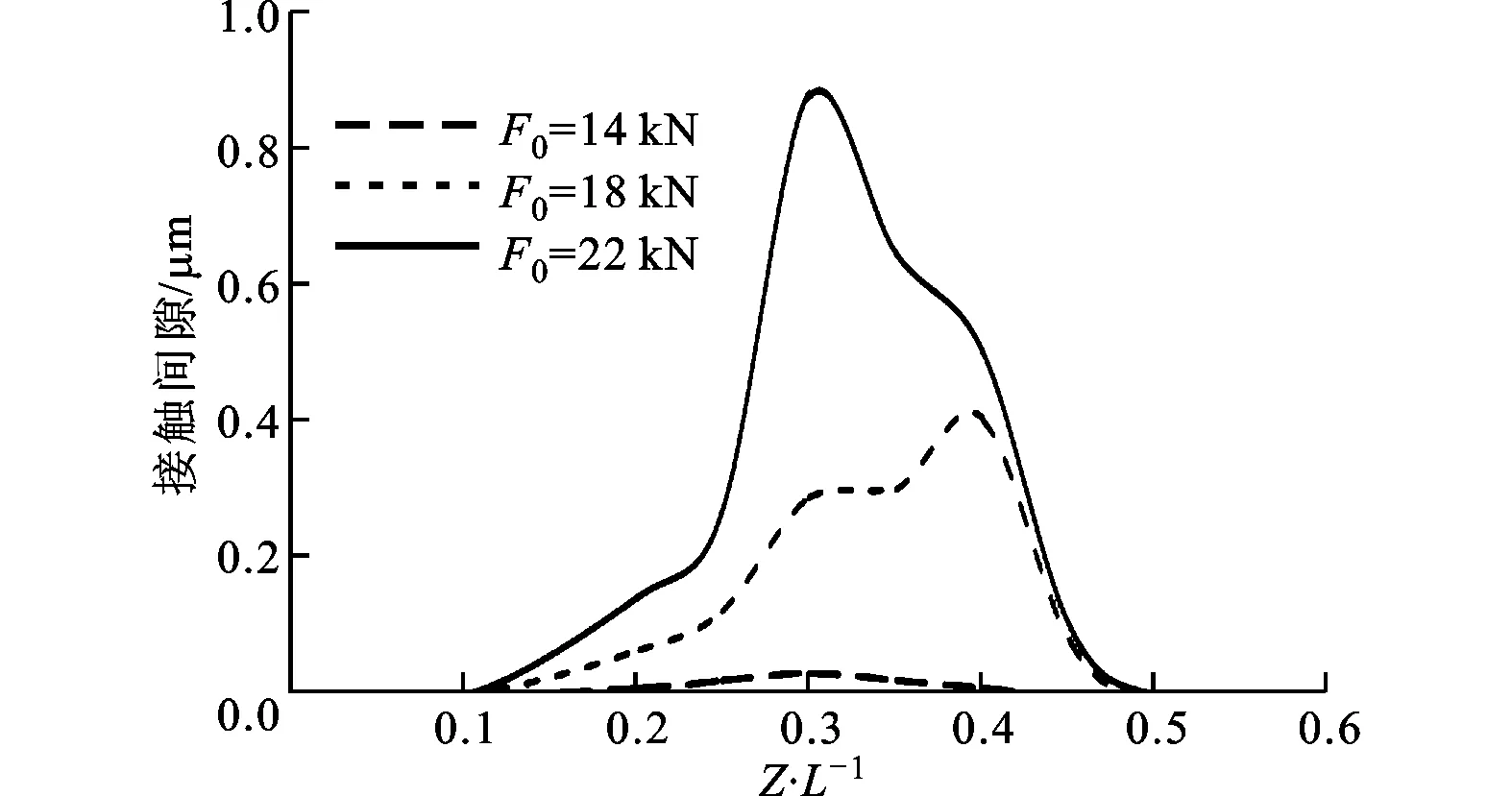
(a)初始拉力對接觸間隙的影響

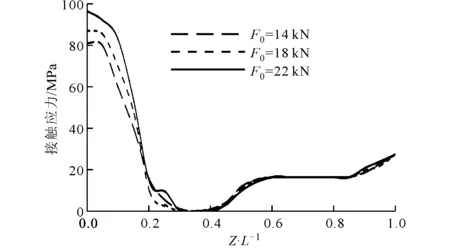
(b)初始拉力對接觸應力分布的影響圖11 初始拉力對接觸間隙和接觸應力分布的影響

ISO標準規(guī)定過盈量至少為12 μm。忽略楔面摩擦,保持該過盈量值不變,轉(zhuǎn)速為0時不同拉力作用下的接觸狀態(tài)如圖11所示,可知刀柄在靜夾緊力作用下薄壁處徑向收縮,呈“馬鞍”狀(見圖11a),從而導致接觸面產(chǎn)生間隙,該間隙隨拉力增加而增大,這是因為初始拉力的存在相當于對薄壁處施加了翻轉(zhuǎn)力矩,從而迫使兩者分離。由于靜拉力下刀柄“收縮”只產(chǎn)生于中前部,故圖中Z/L=0.6(L為刀柄錐面總長,Z為任一點到錐面大端的距離)之后的曲線未畫出。

從圖11b可看出,應力分布與間隙分布恰好相反,接觸應力集中出現(xiàn)在刀柄兩端,最大應力集中于刀柄大端。同時可以看出:初始拉力越大則間隙越大,這成為限制結(jié)合面剛度進一步提高的主要因素,還可能導致切削顫振的發(fā)生。此外,過盈量對接觸應力影響較大,過小的過盈量將不能保證充分接觸。Hanna等的研究證明,若過盈量過小,即使充分提高拉緊力,接觸率仍會小于40%[15]。

2.3.2 動態(tài)夾緊力作用下的接觸間隙與接觸應力分布 由1.3節(jié)和1.4節(jié)可知,動態(tài)夾緊力與初始夾緊力之比隨主軸轉(zhuǎn)速上升而增大,因此可推測主軸轉(zhuǎn)速越高,動態(tài)夾緊力對接觸應力的影響就越大,但同時主軸結(jié)合部也會因膨脹而產(chǎn)生更大的接觸間隙,所以有必要探究動態(tài)夾緊力對消除接觸間隙的作用。為此,假設(shè)靜拉力為0,過盈量仍為12 μm,求出各主軸轉(zhuǎn)速下有、無動態(tài)夾緊力作用時接觸應力的分布,見圖12。

由圖12a、12b可以看出:接觸應力隨主軸轉(zhuǎn)速上升而下降,刀柄兩端應力較大;在夾爪作用下,接觸應力顯著提高,并且隨著主軸轉(zhuǎn)速升高動態(tài)夾緊效果更加明顯;在離心力和動態(tài)力的雙重作用下,薄壁結(jié)合處的間隙值及范圍變大,導致該處應力降低,內(nèi)部間隙減小,在Z/L=0.4～0.8處接觸應力隨主軸轉(zhuǎn)速提高而增大。可見,動態(tài)夾緊力能顯著提高平均接觸應力,但局部應力仍然較低,這是因為夾爪翻轉(zhuǎn)力矩的作用使得薄壁處變形、間隙不能完全消除的緣故。

對比圖12b、12c可見,接觸應力隨摩擦因數(shù)的增大而減小,這與2.2節(jié)的分析是一致的,說明摩擦因數(shù)與夾緊效率密切相關(guān)。

總夾緊力作用下的接觸狀態(tài)可看作上述2種接觸狀態(tài)的疊加,變化規(guī)律相似,故不再贅述。

2.4 靜、動態(tài)夾緊力影響下的主軸自然頻率

以往的研究較少考慮刀桿的作用和結(jié)合面剛度對整體剛度的影響,動態(tài)夾緊力的上升會對主軸剛度產(chǎn)生何種影響也不明確。為此,針對某型號主軸建立包含刀柄系統(tǒng)的主軸三維模型,為節(jié)省計算機資源,建模時忽略拉桿及碟簧組結(jié)構(gòu),并忽略內(nèi)孔、倒角等幾何特征,只保留主軸、刀柄與夾爪結(jié)構(gòu),邊界條件設(shè)置與2.3.1小節(jié)中相同。所建立的主軸簡化三維模型見圖13。

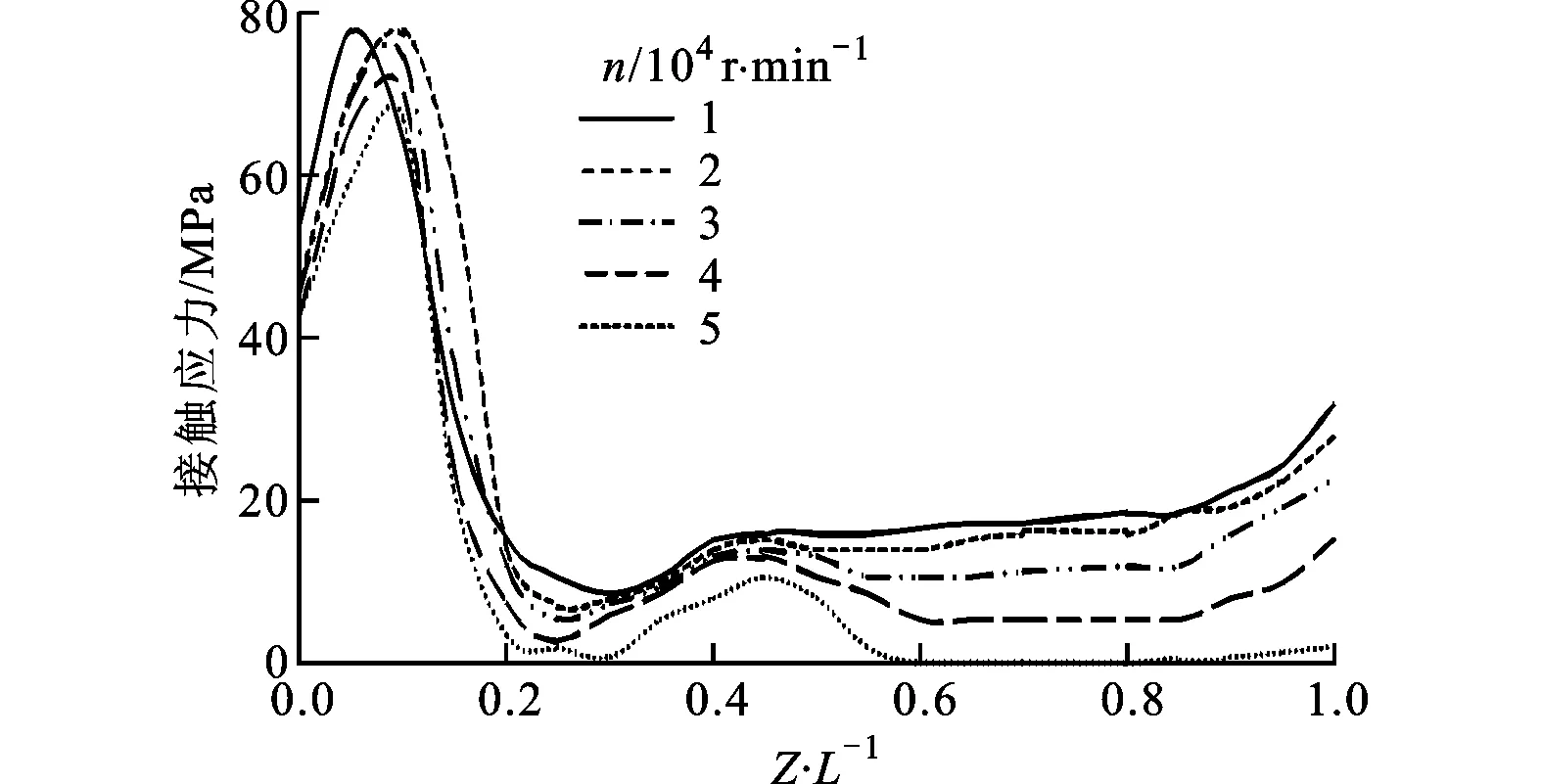
(a)動態(tài)夾緊力為0

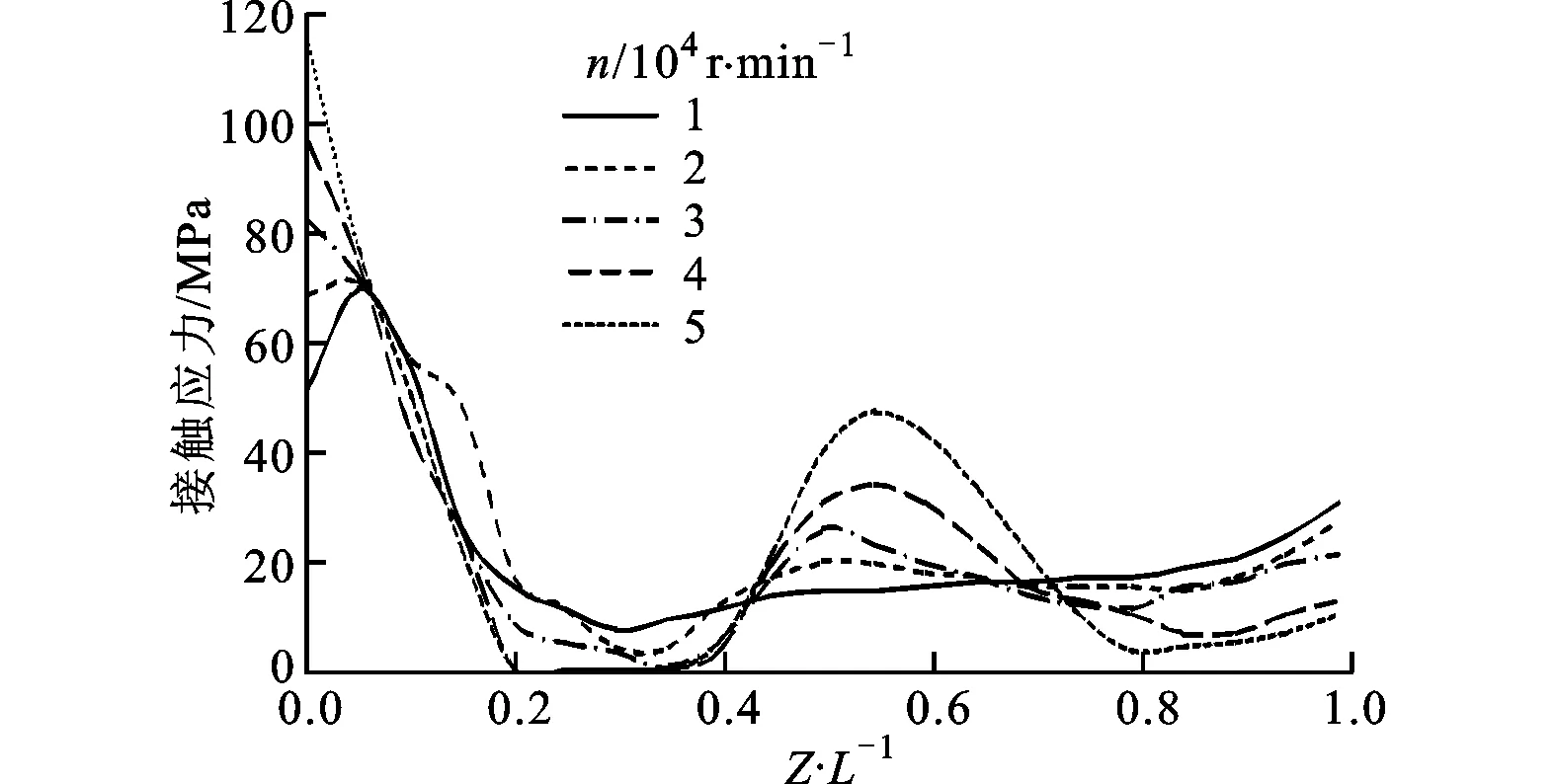
(b)有動態(tài)夾緊力,不計摩擦

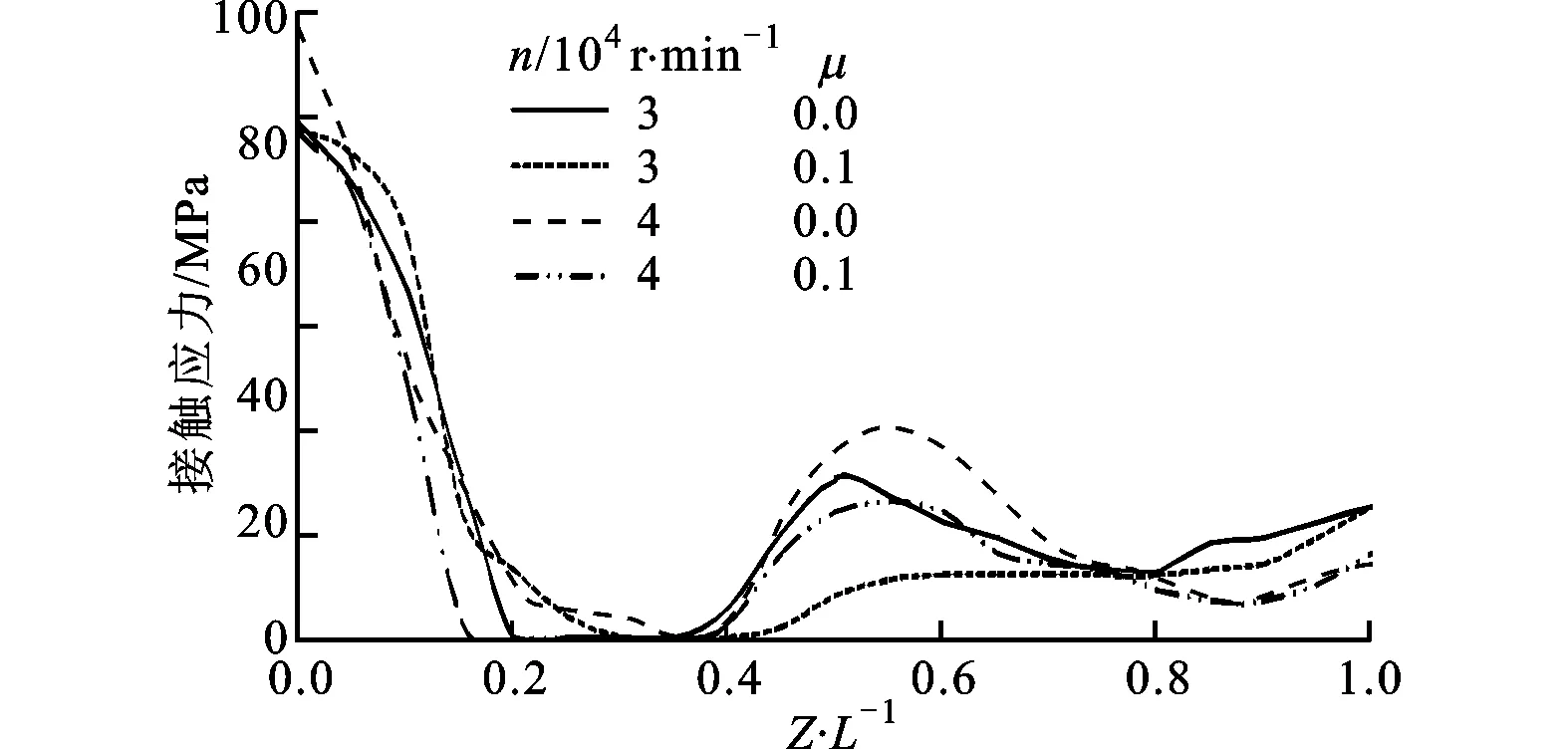
(c)有動態(tài)夾緊力,考慮摩擦圖12 接觸應力分布隨動態(tài)夾緊力和摩擦力的變化

圖13 主軸簡化三維模型

2.4.1 初始拉力對主軸自然頻率的影響 不同初始拉力對主軸前6階自然頻率的影響見表1。靜態(tài)時前2階頻率不受拉力的影響,結(jié)合面剛度與1、2階頻率無關(guān);其他各階頻率都隨拉力上升而減小,但減小幅度不同,例如對于3階頻率,當拉力從6 kN上升到14 kN時,頻率減小了3 Hz,而當拉力從22 kN上升到30 kN時,頻率減小量為11.8 Hz,其他各階頻率的變化情況與此類似。結(jié)合2.3節(jié)的分析和文獻[7]的試驗結(jié)果可以推測:這可能是過大的拉緊力使得結(jié)合面的接觸間隙顯著增大,致使結(jié)合部的阻尼大幅下降,雖然結(jié)合部剛度會隨拉力的增加而輕微上升[7-8],但阻尼的變化最終決定了主軸自然頻率的變化趨勢。

2.4.2 動態(tài)夾緊力對主軸自然頻率的影響 為了說明動態(tài)夾緊力對主軸自然頻率的影響,設(shè)定初始夾緊力為18 kN。表2為主軸僅在初始夾緊力作用下旋轉(zhuǎn)時的頻率變化規(guī)律,可見1、2階頻率隨主軸轉(zhuǎn)速上升而輕微下降,其他各階頻率下降較快,且主軸轉(zhuǎn)速越高頻率變化速率也越大,這主要是由主軸自身的離心膨脹導致的。表3為不同主軸轉(zhuǎn)速下動態(tài)夾緊力對主軸自然頻率的影響,與表2相比可知,在動態(tài)夾緊力作用下,1階頻率略有提升,2階頻率變化速率下降:無動態(tài)夾緊力時,隨主軸轉(zhuǎn)速從40 000 r/min上升到50 000 r/min頻率減小了1.7 Hz,而有動態(tài)夾緊力時頻率只減小了1.1 Hz,但是對于其他各階頻率,隨著主軸轉(zhuǎn)速的提高,動態(tài)夾緊力反而使得頻率下降,進一步說明過高的動態(tài)夾緊力會使結(jié)合面間隙過大,阻尼下降率超過剛度增長率。

由上述分析可知,靜、動態(tài)夾緊力的變化對不同主軸會有不同的影響,使得主軸系統(tǒng)表現(xiàn)出豐富的動態(tài)特征。本文的研究并未考慮刀桿自身的影響,而若加入刀桿的影響,系統(tǒng)頻率又將發(fā)生怎樣的變化?這是有待進一步深入研究的問題。

表1 初始拉力與主軸自然頻率的關(guān)系

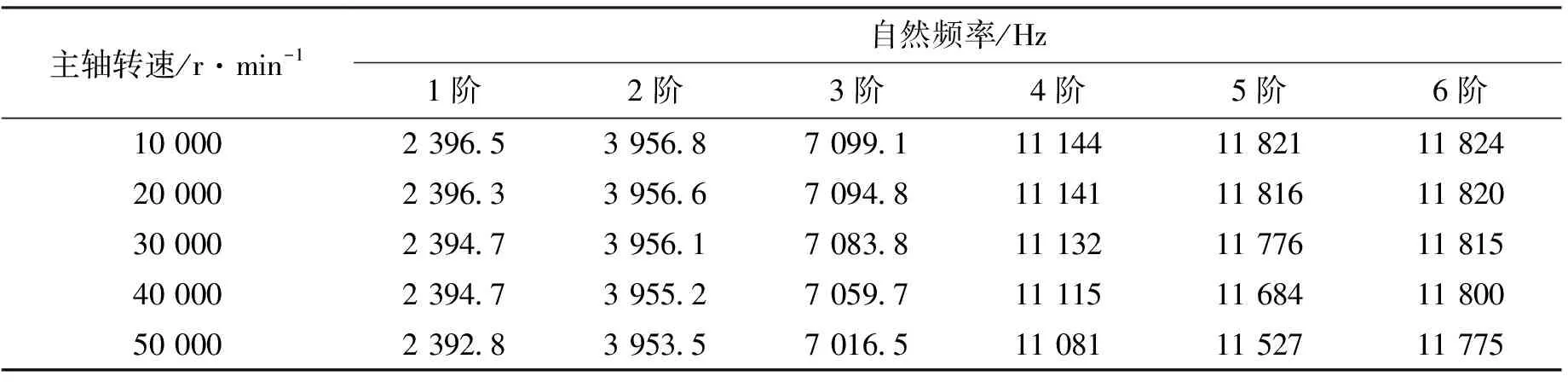
表2 無動態(tài)夾緊力時主軸自然頻率與轉(zhuǎn)速的關(guān)系

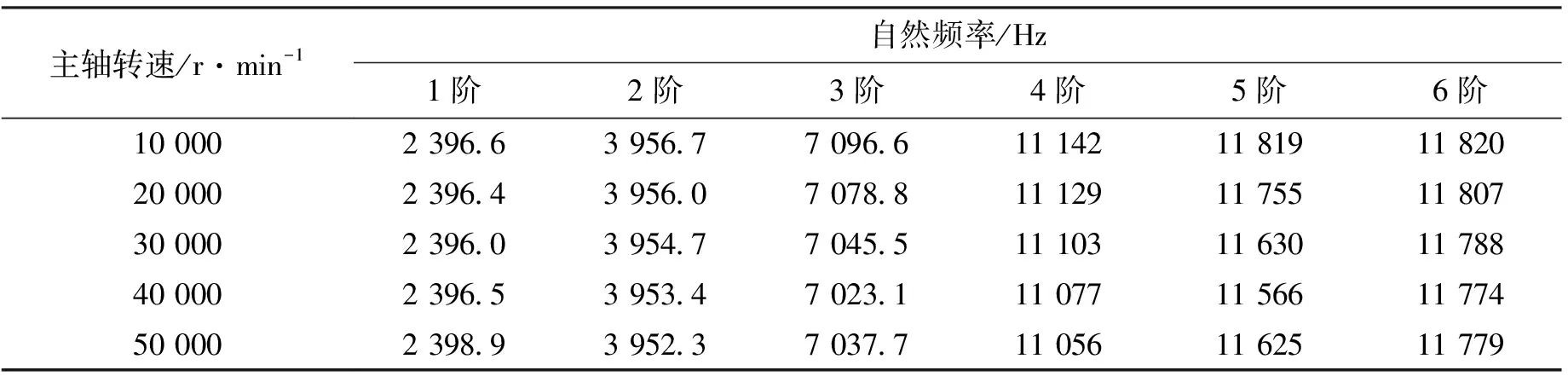
表3 有動態(tài)夾緊力時主軸自然頻率與轉(zhuǎn)速的關(guān)系

3 結(jié) 論

(1)對于本文所研究的拉桿系統(tǒng),在0～50 000 r/min的主軸轉(zhuǎn)速范圍內(nèi)碟簧變形較小,此變形雖然會引起拉桿拉力的變化,但并非主要影響因素,粗略計算時可忽略,但對于超高速PCB鉆孔主軸,其碟簧變形顯著,拉力隨主軸轉(zhuǎn)速下降明顯,并會造成刀柄接觸應力的大幅下降。

(2)HSK A63刀柄的錐面在靜、動態(tài)時都不是完全接觸,而是部分接觸,最大接觸間隙出現(xiàn)于中部,接觸應力則分布于兩端,呈“環(huán)狀”,在過盈量不變時,過大的初始拉力和過高的主軸轉(zhuǎn)速都會減小接觸應力。

(3)結(jié)合面的接觸應力隨主軸轉(zhuǎn)速上升而下降,兩端應力較大。動態(tài)夾緊力會顯著提高結(jié)合面的接觸應力,主軸轉(zhuǎn)速越高,動態(tài)夾緊效果就越明顯。但是,離心力和動態(tài)力的雙重作用使得薄壁結(jié)合處的間隙變大,導致局部應力降低。動態(tài)夾緊力的大小受楔面摩擦因數(shù)的影響:摩擦因數(shù)越大,動態(tài)夾緊力就越小,夾緊效率越低;在不失效的前提下,主軸轉(zhuǎn)速越高這種影響越明顯。

(4)拉桿初始拉力對主軸前2階固有頻率基本無影響,但提高拉力卻能顯著提升其他各階自然頻率。動態(tài)夾緊力的升高會增強刀柄結(jié)合部的剛度,輕微提升前2階自然頻率,并能減小其他各階頻率的變化幅度,但是過高的動態(tài)夾緊力反而會使得刀柄結(jié)合面的間隙過大,導致阻尼減小,從而降低主軸頻率。

[1] CHEN J S, HWANG Y W. Centrifugal force induced dynamics of a motorized high-speed spindle [J]. The International Journal of Advanced Manufacturing Technology, 2006, 30(1/2): 10-19.

[2] 張松, 艾興, 劉戰(zhàn)強, 等. 高速主軸/刀柄聯(lián)接的離心力效應分析 [J]. 工具技術(shù), 2004, 38(2): 7-9. ZHANG Song, AI Xing, LIU Zhanqiang, et al. Analysis for effect of centrifugal force on performance of spindle/toolholder interface at high rotational speed [J]. Tool Engineering, 2004, 38(2): 7-9.

[3] 王貴成, 王樹林, 裴宏杰, 等. 高速加工HSK工具系統(tǒng)動態(tài)特性的研究 [J]. 中國機械工程, 2006, 17(5): 441-445. WANG Guicheng, WANG Shulin, PEI Hongjie, et al. Study on the dynamic characteristics of HSK tooling system in high speed machining [J]. China Mechanical Engineering, 2006, 17(5): 441-445.

[4] 張國軍, 臧運峰, 呂楓, 等. 數(shù)控機床HSK刀柄和主軸在高速旋轉(zhuǎn)下的連接性能分析 [J]. 中國機械工程, 2012, 23(6): 631-636. ZHANG Guojun, ZANG Yunfeng, Lü Feng, et al. Analysis of toolholder-spindle interface at high rotational speed for CNC machine tools [J]. China Mechanical Engineering, 2012, 23(6): 631-636.

[5] JIANG S, ZHENG S. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics [J]. International Journal of Machine Tools and Manufacture, 2010, 50(1): 131-142.

[6] CHEN Y S, CHIU C C, CHENG Y D. Dynamic analysis of disc spring effects on the contact pressure of the collet-spindle interface in a high-speed spindle system [J]. Proceedings of the Institution of Mechanical Engineers: Part C Journal of Mechanical Engineering Science, 2009, 223(5): 1191-1201.

[7] AOYAMA T, INASAKI I. Performances of HSK tool interfaces under high rotational speed [J]. CIRP Annals: Manufacturing Technology, 2001, 50(1): 281-284.

[8] HUNG J P, LAI Y S, LUO T L, et al. Effect of drawbar force on the dynamic characteristics of a spindle-tool holder system [J]. International Journal of Mechanical, Aerospace, Manufacturing, Industrial Science and Engineering, 2014, 8(5): 983-988.

[9] ALMEN J O, LASZLO A. The uniform-section disk spring [J]. Transactions of ASME, 1936, 58: 305-314.

[10]BAGAVATHIPERUMAL P, CHANDRASEKARAN K, MANIVASAGAM S. Elastic load-displacement predictions for conedisc springs subjected to axial loading using the finite element method [J]. The Journal of Strain Analysis for Engineering Design, 1991, 26(3): 147-152.

[11]李光輝, 馮平法. HSK刀柄與主軸聯(lián)結(jié)性能的有限元分析 [J]. 工具技術(shù), 2005, 39(9): 27-30. LI Guanghui, FENG Pingfa. Finite element analysis of HSK toolholder and spindle interface [J]. Tool Engineering, 2005, 39(9): 27-30.

[12]陳世平, 石軍. 高速加工工具系統(tǒng)夾緊機構(gòu)分析 [J]. 工具技術(shù), 2010, 44(2): 72-74. CHEN Shiping, SHI Jun. Analysis on the clamping mechanics of tool system for high speed machining [J]. Tool Engineering, 2010, 44(2): 72-74.

[13]徐秉業(yè), 劉信聲. 應用彈塑性力學 [M]. 北京: 清華大學出版社, 1995: 203-205, 237-241.

[14]OZAKI S, TSUDA K, TOMINAGA J. Analyses of static and dynamic behavior of coned disk springs: effects of friction boundaries [J]. Thin-Walled Structures, 2012, 59: 132-143.

[15]HANNA I M, AGAPIOU J S, STEPHENSON D A. Modeling the HSK toolholder-spindle interface [J]. Journal of Manufacturing Science and Engineering, 2002, 124(3): 734-744.

(編輯 葛趙青)

Dynamic Characteristics of Rotor-Draw Bar System in High-Speed Spindle under Influence of Centrifugal Force

LI Te1,2,RUI Zhiyuan1,2,LEI Chunli1,2,HU Chibing1,2,LIU Jun1,2

(1. Key Laboratory of Digital Manufacturing Technology and Application, The Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China; 2. College of Mechano-Electronic Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

In order to further clarify the influence of centrifugal force on the dynamic characteristics of high-speed spindle system, a contact model of toolholder is established by taking the rotor-draw bar system as the research target, and considering the radial extension of disc spring under centrifugal force. The relationship between the tension caused by deformation of disc spring and the rotation speed is investigated. On this basis, the changing rule of the contact stress of toolholder with the initial tension force and the dynamic clamping force is studied, hence the effect of these changes on the natural frequency of the rotor system is revealed. The result shows that the radial extension of disc spring will cause a reduction of the tension of draw bar, and the decrease of tension is related to the geometry size and initial tension force. For the spindle with small tension force, the influence is remarkable; while it can be neglected for the spindle with large tension force. The clamping efficiency under initial force or dynamic clamping force decreases with the increase in rotating speed. The contact stress can be raised by increasing the dynamic clamping force. However, an excessive clamping force will increase the contact clearance and reduce the damping at joint interface, and finally decrease the natural frequency of the rotor system.

high-speed spindle; draw bar; centrifugal force; disc spring; contact stress; natural frequency

2014-07-26。 作者簡介:李特(1987—),男,博士生;芮執(zhí)元(通信作者),男,教授。 基金項目:國家自然科學基金資助項目(51465035);國際科技合作項目(2011DFR70670)。

時間: 2014-12-24

網(wǎng)絡(luò)出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141224.1607.005.html

10.7652/xjtuxb201503017

TG502

A

0253-987X(2015)03-0104-09