出水超空泡的形狀與弗勞德數影響的實驗研究

賈會霞,胡俊輝,施紅輝,陳波

(浙江理工大學流體工程系,310018,杭州)

?

出水超空泡的形狀與弗勞德數影響的實驗研究

賈會霞,胡俊輝,施紅輝,陳波

(浙江理工大學流體工程系,310018,杭州)

潛射導彈/射彈超空泡出水時超空泡與界面的作用機理目前還不完全清楚,而非定常流重力作用下的超空泡形狀的描述也需要進一步探討。為此,進行了水下高速射彈超空泡出水的實驗研究,用高速攝影儀拍攝了航行體出水過程中空泡形狀變化的圖像,測量分析了各種不同頭型航行體誘導的空泡尺寸、輪廓和生成潰滅形態的變化規律,并將研究結果與已有的理論公式和半經驗公式進行了對比。研究表明,對所研究的工況,Savchenko半經驗公式的適用范圍可以擴展到空化數小于0.12;此外,實驗測得的超空泡歸一化長度亦高于考慮弗勞德數影響的Vasin的理論值,文中采用一系數對該公式進行了修正。實驗研究還發現,航行體頭型對超空泡的尺寸影響較大,超空泡與自由液面接觸后,空泡直徑有一定程度的增大。

超空泡;出水;高速射彈;超空泡形狀

當物體在水下高速運動時,物體周圍的液體壓力降低,當物體速度達到一定程度時,液體會發生氣化,在物體周圍形成空泡,當空泡包裹住整個物體表面時,這種現象被稱為超空泡。水中運動物體誘導的超空泡流動是一個典型的氣-液兩相流問題。利用超空泡技術可以大大降低水下運動物體的黏性阻力,實現減阻提速的效果,在水中兵器、水下運輸、海上急救等方面有著廣泛的應用[1]。

水下航行體超空泡出水問題是超空泡流動的一個重要分支,航行體的運動方向為垂直亦或是傾斜向上,主要應用在水下潛艇或者水下潛射導彈上[2]。國外的Waugh、Xing-Kaeding等對航行體帶空泡出水過程中自由液面和空泡的潰滅以及重力的影響規律進行了實驗研究[3-4];國內的魯傳敬教授利用CFD方法以及動網格技術對細長體出水過程中航行體受力波動、液面的升高、航行體尾部拖水等問題進行了研究[5],王一偉等對典型航行體模型水下發射的全過程進行數值模擬,得到了航行體周圍空泡演化過程、表面壓力分布變化、航行體關鍵截面的全時程載荷響應[6]。

空泡的形態及其形成機理和影響因素研究一直是該領域的研究重點,因為空泡的幾何形態直接關系到水下航行體的受力情況,對航行體的穩定性有著重要的影響。國內外學者開展了大量的研究工作,Munzer-Reichardt、Logvinovich、Savchenko等提出了描述空泡形狀的理論公式和半經驗公式[7-9],Parishev和Vasin提出了考慮重力效應時的空泡形狀理論公式[10-11];曹偉、周素云等利用實驗手段對水平自然射彈空泡的形態進行了研究[12-13],張學偉、劉海旻等應用數值仿真方法研究了空泡的形態[14-15]。自然空化空泡在出水過程中,不可避免地會受到重力和自由面的影響,因此其形態變化更為復雜,目前國內外相關方面的研究還比較少。本文利用高速射彈模型實驗和高速攝影方法,研究了不同模型和參數下自然空化超空泡出水形態尺寸的變化規律。

1 實驗裝置

1:工控計算機;2:高速攝影儀;3:照明燈;4:高壓氣源;5:航行體捕獲器;6:觀察窗;7:水箱支撐架;8:法蘭;9:球閥;10:防水隔膜;11:法蘭蓋板;12:發射管;13:電磁閥;14:高壓氣缸圖1 高速物體出水實驗裝置示意圖

實驗的研究工作是在一套高速航行體出水實驗系統中進行的,實驗裝置如圖1所示。該系統主要由發射裝置、觀察裝置和測量裝置3部分組成。其中,測量裝置包括工控計算機、高速攝影儀和照明燈,發射裝置由高壓氣源、高壓氣缸、電磁閥和發射管等構成。發射裝置為一臺一級輕氣炮,在實驗時,通過調節高壓氣缸內氣體壓力驅動發射管中航行體高速運動。本實驗采用高壓氮氣驅動,壓力范圍為0～2.5 MPa,可以使航行體加速到100 m/s以上。觀察裝置包括航行體捕獲器、觀察窗、法蘭、球閥、防水隔膜和法蘭蓋板。航行體從發射管加速射出后,垂直向上地沖破防水隔膜進入水箱,在水中形成超空泡;此時,采用高速攝影儀(美國Cooke公司的pco.1200s)記錄整個過程,攝影所需的光源由3盞1 kW的照明燈提供。實驗裝置的具體構造和實驗步驟可以參照文獻[16-17],這里不再贅述。

本研究對多種模型的航行體進行了射彈實驗,此處只給出幾種。實驗采用的航行體模型的外形及其尺寸如圖2所示,表1給出了相關參數,模型的材料為鎂鋁合金。在本文中將采用1#～4#來分別代表所研究的不同航行體模型。

進行后期的實驗數據處理時,需要確定拍攝圖片尺寸與實際尺寸之間的縮放比例,本文采取的方法是在實驗前拍攝直尺圖像(見圖3),根據直尺上的刻度取得圖像的縮放比例。

表1 幾種不同形狀的航行體模型(Dn=6 mm)

注:Dn為航行體特征直徑。

由于空泡、水、有機玻璃觀察窗的折射會導致圖像各部分的比例不均勻,相關研究[18]表明這種誤差的影響較小,一般在0.3%～0.6%,可不予考慮。

空化數是空泡流動中一個很重要的參數,其表達式如下

(1)

式中:p∞表示物體前方未擾動處液流靜壓,計算中一般取為當地大氣壓力與航行體的注水靜壓力之和;pc為空泡內的壓強,在自然空泡實驗中取為飽和蒸汽壓力pv;V∞是物體相對來流的速度,射彈實驗中為射彈的速度,實驗中采用相鄰兩張照片之間的平均速度;ρ為流體的密度。

重力因素對空泡外形特征也會產生影響,考慮重力因素的弗勞德數的表達式為

(2)

式中:Fr為弗勞德數;g為重力加速度;Dn為航行體特征直徑。

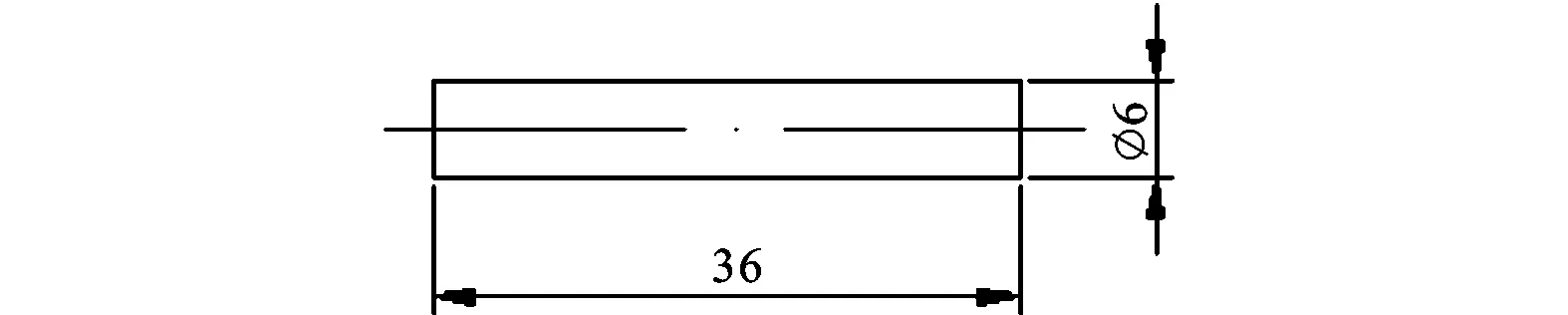
(a)1#模型

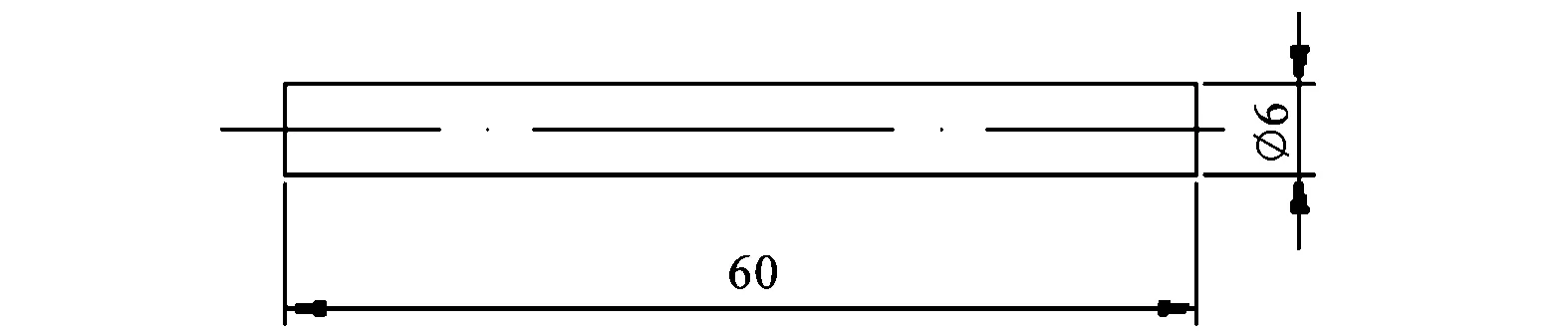
(b)2#模型

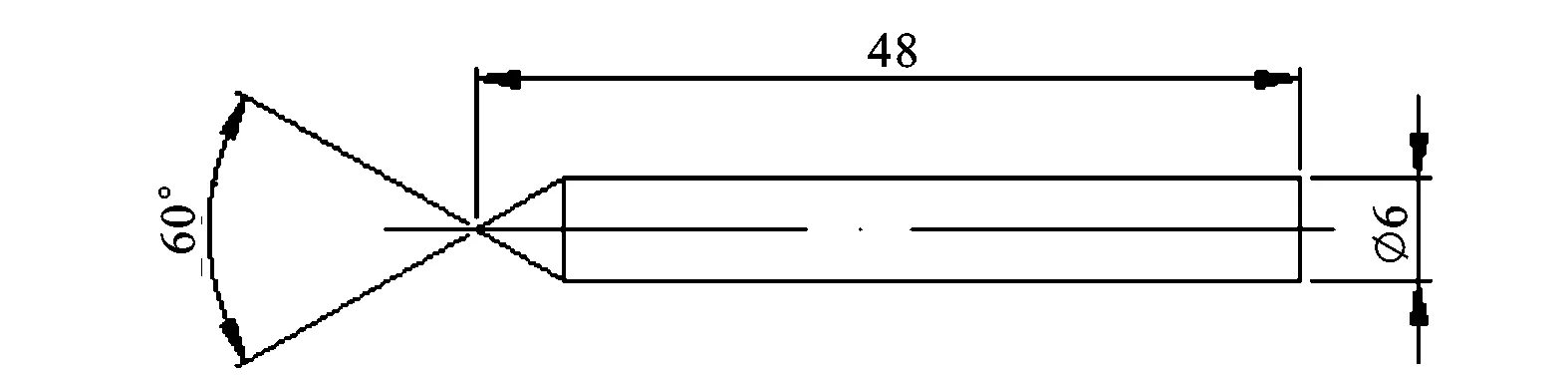
(c)3#模型

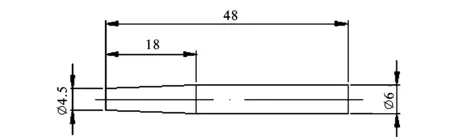
(d)4#模型單位: mm圖2 實驗航行體模型的尺寸

圖3 高速攝影儀拍攝的直尺圖片

2 實驗結果和分析

2.1 自然超空泡從生成到潰滅的形態變化

圖4示出了4#射彈模型(空化器直徑為4.5 mm的圓臺型航行體)的出水全過程。本文實驗的拍攝速度為4 000幀/s,即相鄰兩張照片的時間間隔為0.25 ms。航行體經水箱下方打開的球閥進入水箱,從下向上運動。當航行體進入可視觀察窗時,航行體的速度為63 m/s。因為航行體的速度較高,在航行體周圍產生了較大尺寸的超空泡。在圖4(16)中可看到完整的超空泡。航行體在阻力和自身重力的作用下(其中阻力起主導作用)速度逐漸減小,對應的超空泡的尺寸也有所減小,這在后續給出的結果中也可看出。

該工況因為航行體入水速度較大,因而一直到出水時刻(見圖4(23))超空泡形狀都較穩定,并未出現自尾部至頭部的空泡潰滅和再生成,當航行體出水時才發生空泡的潰滅。

當航行體從下向上運動時,包裹航行體的超空泡因為航行體的運動,超空泡所在的水位也在不斷地減小,即使在同一時刻,超空泡自身在長度方向上受到的水壓也是不同的。因此,為了研究出水超空泡的形狀變化特性,選取了3個水深進行研究。以水面自由面為0點,向上為正方向,水深h分別取-265.43、-153.77、-81.89 mm。

定義航行體頭部到達固定水位的時刻為0,用航行體特征直徑(Dn=6 mm,見圖2)對空泡直徑Dc進行歸一化。航行體以不同速度穿過選取的不同水位時,歸一化直徑隨時間的變化關系如圖5所示。由圖可知:航行體穿過固定水位時,空泡經歷了快速擴張、緩慢變化、快速收縮的過程;空泡生長到潰滅的時間為3.5～4.25 ms。-265.43、-153.77 mm水位處的空泡歸一化直徑都近似地呈拋物線形式,在t=2 ms時達到峰值;h=-81.89 mm水位處,空泡直徑并沒有像其他水位那樣在2 ms時達到峰值,而是接著擴張到2.5 ms時才達到峰值。其原因可能是:在其他兩個水位處,空泡從形成到潰滅,航行體都在水下,尚未越過自由水面,而對于h=-81.89 mm的水位,圖5中橫坐標的2 ms時刻正好對應圖4(23)所示的航行體出水以及超空泡開始接觸空氣的時刻,在自由液面和浮力等的影響下,空泡頭部的縱向體積增長被抑制,空泡尾部橫向地擴張,從而導致在此水位空泡直徑的繼續膨脹增長,延緩了潰滅。

(1) (2) (3) (4) (5) (6) (7) (8)

(9)(10)(11)(12)(13)(14)(15)(16)

(17)(18)(19)(20)(21)(22)(23)(24)

(25)(26)(27)(28)(29)(30)(31)(32)圖4 圓臺型航行體模型的出水全過程

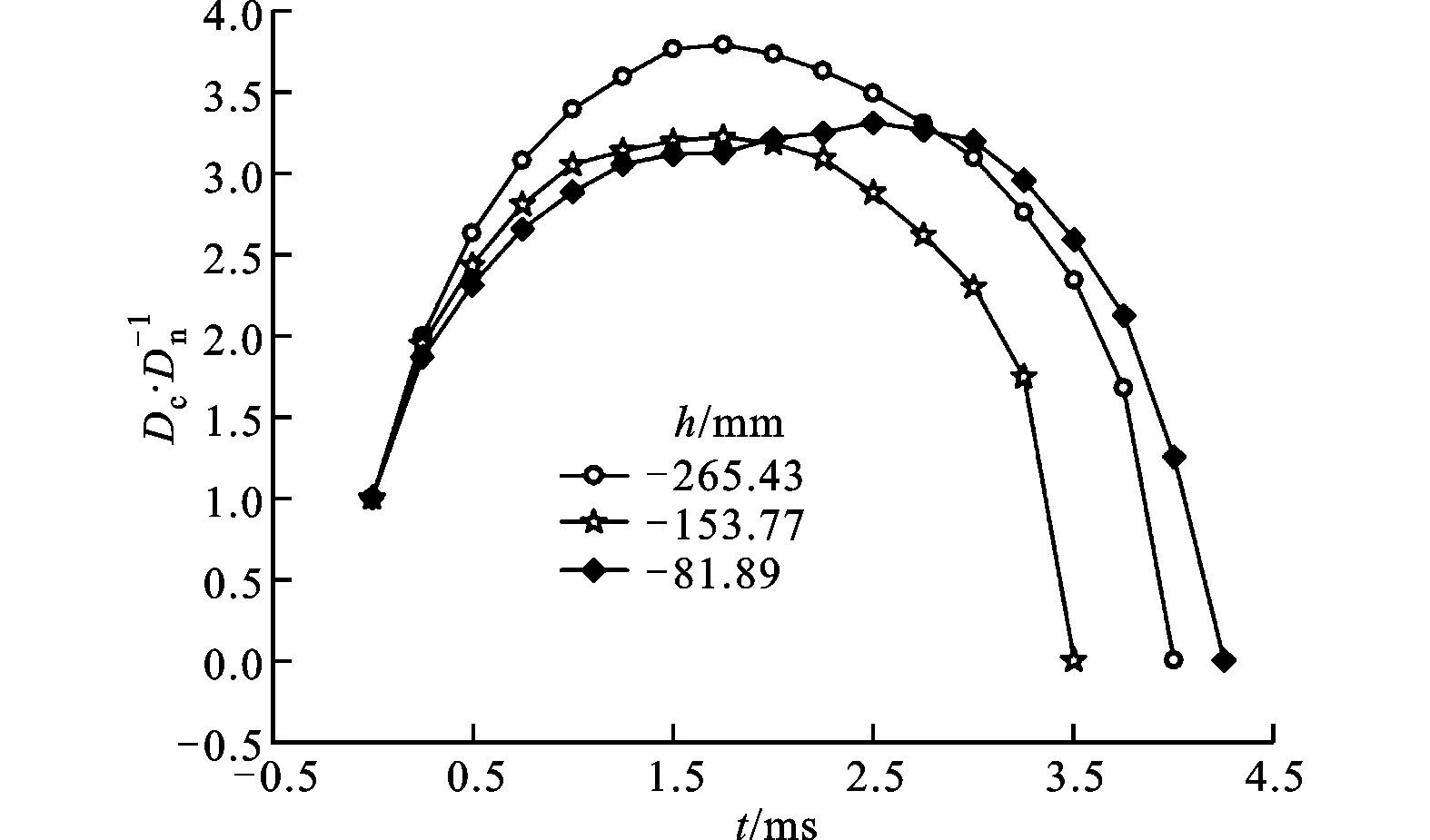
圖5 不同水位處空泡形態變化

2.2 出水自然空化超空泡的尺寸變化

超空泡的形狀會影響航行體在水中所受到的阻力。超空泡的長度和直徑采用航行體特征直徑Dn進行歸一化。

圖6給出了4種航行體的歸一化長度隨空化數的變化與理論和半經驗公式的對比。據式(1)計算空化數σ時,式中的p∞取航行體頭部所在位置處的水靜壓強和當地大氣壓之和。須注意的是,此處并未考慮Fr的影響(Fr的影響隨后討論)。圖中帶符號的4條實線為本文的實際測量數據;實線為根據Logvinovich所提出的空泡截面獨立膨脹原理[8]計算得到的結果;長虛線為根據Savchenko提出的半經驗公式[9]計算得到的結果,它適用的空化數范圍在1×10-4～1.2×10-2內;短虛線(幾乎與實線相重合)是根據Munzer-Reichardt[7]模型計算得到的結果。該模型是賴卡特基于低階勢流理論方程導出的,他所給出的空泡形狀如下

(3)

(4)

cd=cx0(1+σ+0.028σ2)

(5)

式中:Dn表示空化器特征直徑;cd為空化器阻力系數;cx0為σ=0時的阻力系數,對于圓盤空化器,取cx0=0.805。

從圖6中可看到,所有的實驗數據都要高于Logvinovich和Reichardt的理論公式值,而低于Savchenko的半經驗值。

2#和4#航行體與Savchenko所給出的數值非常接近。1#航行體的實驗數據介于Logvinovich和Savchenko的值之間,變化趨勢與理論和半經驗公式相似。

從圖6中還可看到,對于上述3種工況(即1#、2#和4#),隨空化數的增大,空泡的歸一化尺寸都逐漸減小,且變化趨勢基本一致。對比1#和2#的結果發現,在相同的空化數時,2#航行體的歸一化空泡長度要大于1#的值(這兩種工況進行歸一化的空化器直徑是相同的)。3#航行體的超空泡歸一化長度隨空化數的變化趨勢較為平緩,這可能是因為:一方面,理論公式只是用來描述圓盤空化器航行體產生的空泡,而3#為60°錐角航行體,它的頭部繞流情況和平頭空化器頭部繞流相差很大,產生的空泡要小一些;另一方面,60°錐頭時超空泡的尾部潰滅影響范圍較大,這使得超空泡的尺寸難于測量。

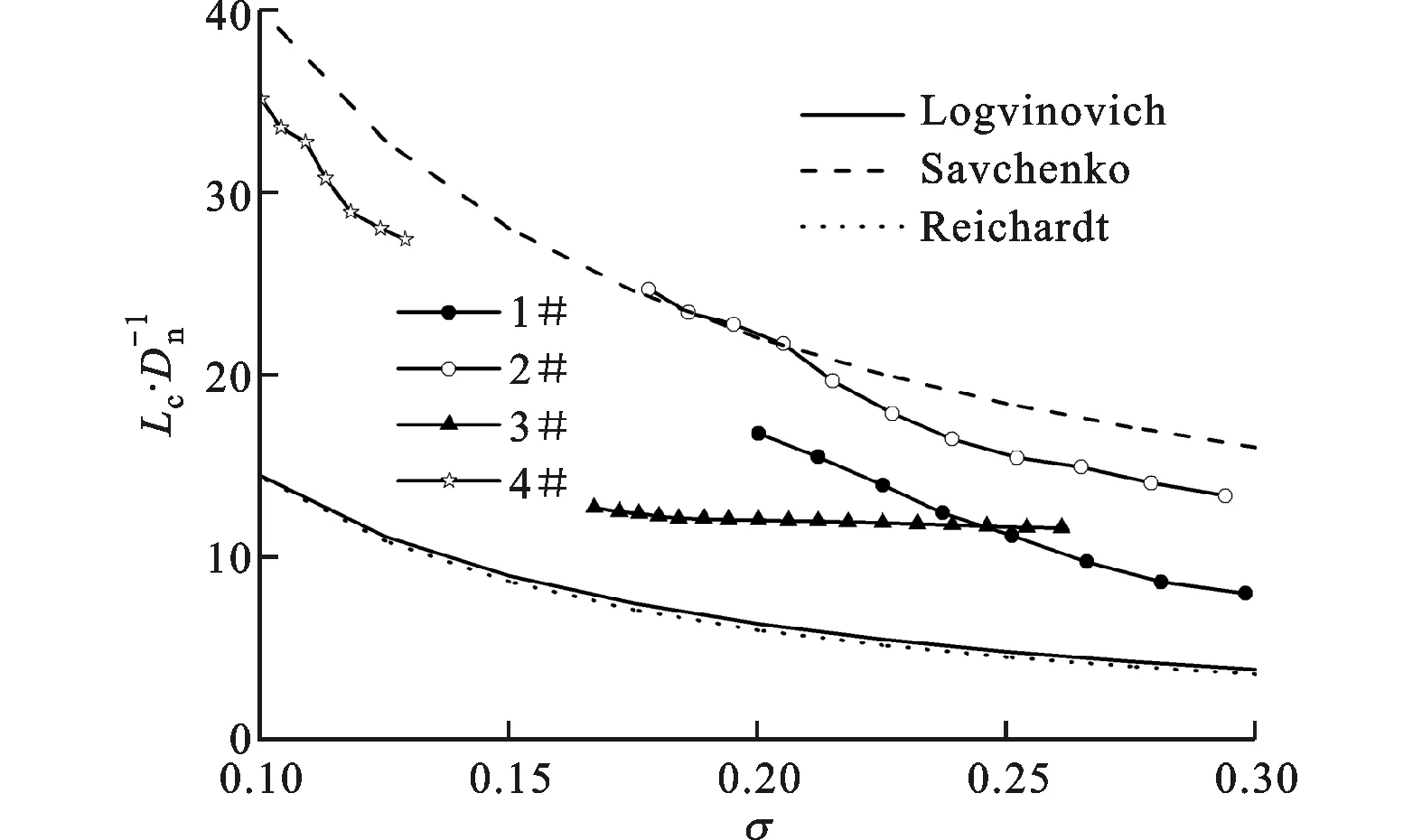
圖6 歸一化長度隨空化數的變化規律

圖7為實驗測得的幾種工況超空泡歸一化直徑與理論和半經驗數據的對比。

從圖7中可看到,4#航行體的實驗數據與Savchenko給出的半經驗公式的數值符合很好,但對于其他3種工況,則或高于半經驗公式給出的較大值,或低于理論公式給出的較低值。其原因一方面可能是因為本文所實驗的航行體的最大直徑不大,只有6 mm,而在實驗時存在著各種測量上的誤差,如實驗時空泡、水、有機玻璃觀察窗的折射,以及實驗后超空泡尺寸測量時的誤差。除此之外,當超空泡尺寸相對較小時,超空泡的尾部潰滅也會影響超空泡的測量結果。

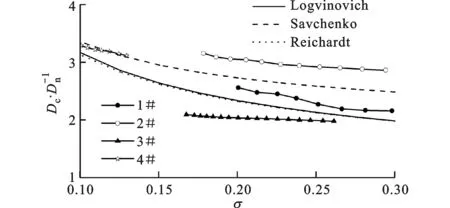
圖7 歸一化直徑隨空化數的變化規律

對于重力場中的超空泡流動,當考慮重力效應時,需引入Fr。Vasin給出了考慮Fr時超空泡長度的計算公式[10-11]

(6)

式中:a=2;k為本文引入的一修正系數,當k=1時,即為Vasin所給出的公式。

圖8給出了實驗數據和Vasin公式計算結果的對比。從圖中可看到,對所實驗的4種航行體,超空泡的歸一化長度都要高于Vasin所給出的計算值。

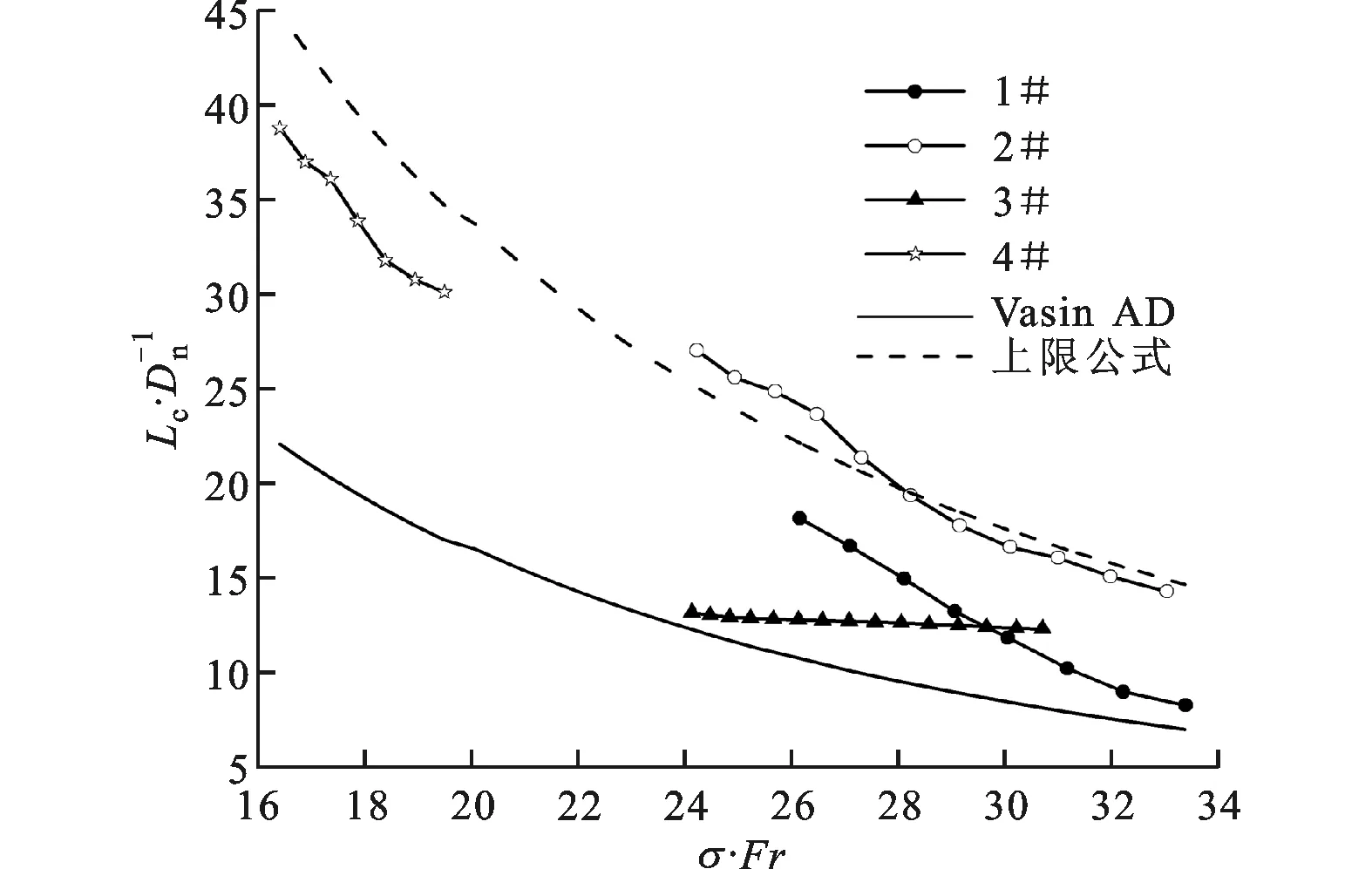
圖8 歸一化長度隨空化數與弗勞德數乘積的變化規律

對比圖8與圖6可以發現,圖8中的實線與Logvinovich和Reichardt的理論值接近。因此,本文在式(6)中引入一系數k=2對Vasin表達式進行修正。圖8中的虛線即為本文得到的k=2時的經驗表達式,用上限公式標注。對于垂直出水超空泡,當考慮重力效應時,超空泡歸一化長度可能介于k=1和k=2之間。

2.3 出水自然空化超空泡的輪廓分析

如圖9所示,以航行體頭部為坐標原點,空泡軸線為x軸,x處的空泡直徑為D(x),分別測量不同x位置的空泡直徑,即可得到在某空化數下的空泡輪廓。

為方便研究比較,對空泡輪廓參數同樣采用航行體特征直徑Dn進行歸一化處理,具體定義如下

此處,只給出了一個工況下(平頭長徑比為12時)3個空化數實驗得到的結果,3個空化數分別為0.147、0.155、0.163。圖10給出了實際測量的3個空化數下的空泡圖像,從該圖中并不能直觀地看出不同空化數時空泡輪廓曲線的不同。

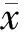
圖9 空泡輪廓的測量方法示意圖

(a)σ=0.147 (b)σ=0.155 (c)σ=0.163圖10 不同空化數的空泡形狀(平頭長徑比為12)

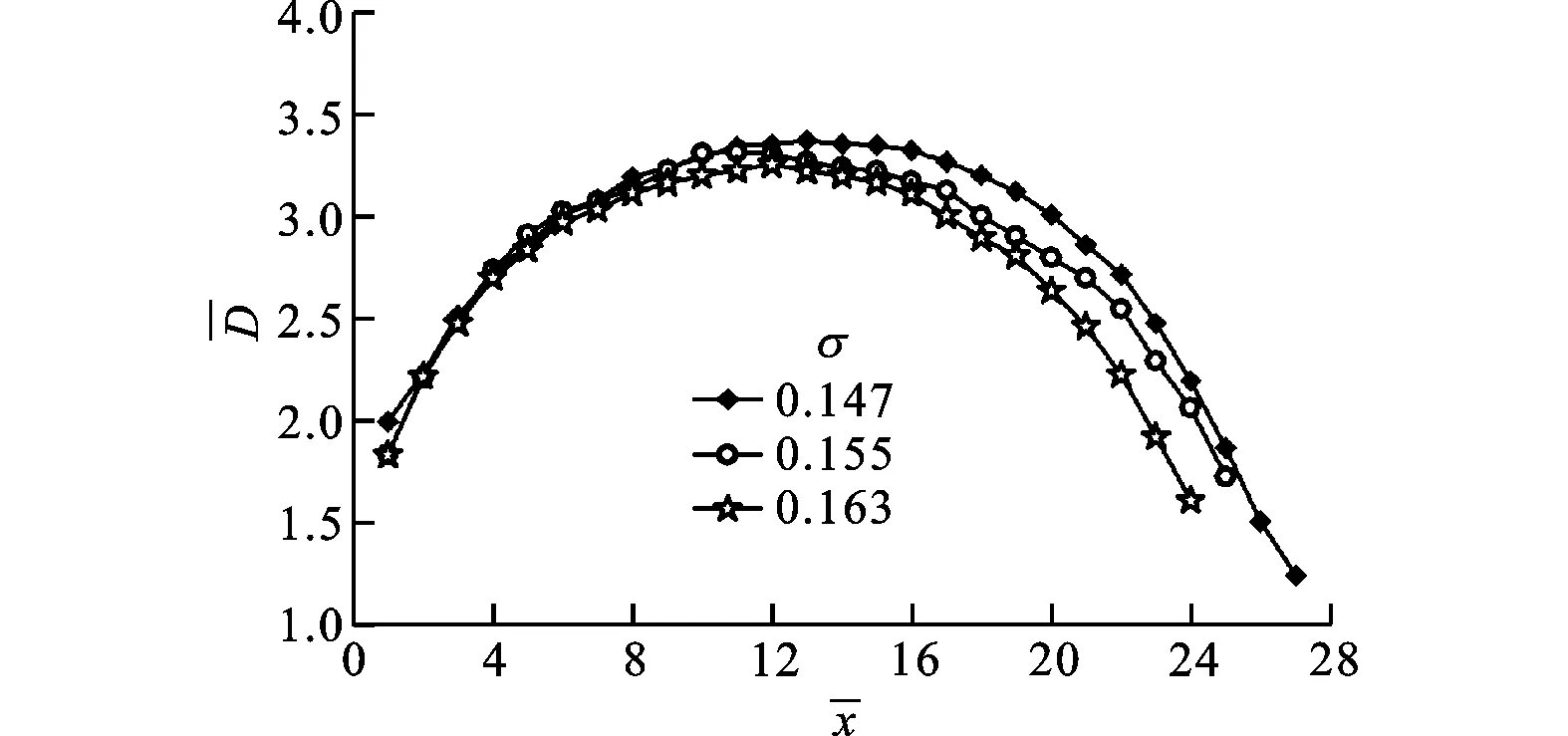
圖11 不同空化數下空泡外形輪廓曲線(平頭長徑比為12)

Logvinovich和Reichardt提出的描述空泡輪廓的理論公式如下

(7)

(8)

圖12給出了空化數為0.155時實驗測得的空泡外形輪廓曲線與Reichardt和Logvinovich公式的理論值對比。Reichardt和Logvinovich的理論曲線為對稱的橢圓弧形,兩種理論曲線峰值相同,但Reichardt曲線的其余部分低于Logvinovich的理論曲線。

在該實驗工況下,實驗數據和理論公式值吻合較好,各空化數下空泡輪廓的前半部分實驗數值比Logvinovich的理論數值小,但比Reichardt的理論數值大,空泡輪廓的后半部分實驗數值更接近Reichardt的理論數值。實驗測得的空泡曲線不對稱,空泡后半部分的直徑要小于前半部分對應位置處的直徑,其原因可能是垂直出水的空泡受到重力的作用,在空泡表面上的縱向壓力梯度使得尾部空泡收縮所致。

圖12 空泡外形輪廓實驗數據與理論值的對比(空化數為0.155)

3 結 論

(1)在高速攝影照片中設定歐拉控制面,讓空泡通過控制面,得知了空泡直徑經歷了快速擴張、緩慢變化、快速收縮的過程;自由液面對臨出水空泡的徑向收縮有抑制作用,并促使空泡直徑有一定程度的增大,空泡潰滅時間增加。

(2)對本文所給出的工況,Savchenko所給出的半經驗公式的適用范圍可以擴展到空化數為0.12的情況,此時實驗數據與半經驗值符合較好。實驗測得的超空泡歸一化長度值都高于Logvinovich和Reichardt的理論計算值。相同空化數下,航行體頭型對空泡的歸一化尺寸影響較大。減小航行體頭部錐角會大幅度地降低空泡尺寸。

(3)對所實驗的幾種工況,當引入考慮重力效應的弗勞德數時,實驗測得的超空泡歸一化長度基本上在Vasin的理論計算值的1倍到2倍之間。

(4)出水超空泡的輪廓在最大空泡直徑處的兩側不完全對稱,后半部分尺寸略小。這可能是因為在重力的作用下,垂直出水空泡表面的縱向壓力梯度使得尾部空泡收縮所致。

[1] 姜百匯, 馬春勛, 劉樂華. 國外超空泡技術及其應用 [J]. 飛航導彈, 2008(5): 20-24. JIANG Baihui, MA Chunxun, LIU Lehua. The technology and its application of supercavitation in foreign [J]. Winged Missiles Journal, 2008(5): 20-24.

[2] 姚奕, 聶永芳, 馮林平. 潛射導彈運載器水下發射關鍵技術研究 [J]. 飛航導彈, 2010(2): 56-60. YAO Yi, NIE Yongfang, FENG Linping. The key technology research of submarine missile carrier launching underwater [J]. Winged Missiles Journal, 2010(2): 56-60.

[3] WAUGH J G, STUBSTAD G W. Water-exit behavior of missiles: part 1 Preliminary studies, AD273717 [R]. China Lake, California, USA: Underwater Ordnance Department, 1961.

[4] XING-KAEDING Y, JENSEN G, PERIC M. Numerical simulation of water-entry and water-exit of a horizontal circular cylinder [C]∥Proceedings of the 6th International Conference on Hydrodynamics. Beijing, China: The Chinese Society of Theoretical and Applied Mechanics, 2004: 663-669.

[5] 魯傳敬, 李杰. 水下航行體出水空泡潰滅過程及其特性研究 [C]∥第十一屆全國水動力學學術會議暨第二十四屆全國水動力學研討會并周培源教授誕辰110周年紀念大會文集. 無錫: 海洋出版社, 2012: 54-67.

[6] 王一偉, 黃晨光, 杜特專, 等. 航行體垂直出水載荷與空泡潰滅機理分析 [J]. 力學學報, 2012, 44(1): 39-48. WANG Yiwei, HUANG Chenguang, DU Tezhuan, et al. Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical launching process [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 39-48.

[7] REICHARDT H. The laws of cavitation bubbles at axially symmetrical bodies in a flow, No. 766 [R]. Spring Quarry, Great Britain: Ministry of Aircraft Production, 1946: 322-326.

[8] LOGVINOVICH G V. 自由邊界流動的水動力學 [M]. 施紅輝, 譯. 上海: 上海交通大學出版社, 2012: 97-122.

[9] SAVCHENKO Y N. Experimental investigation of supercavitating motion of bodies [C]∥VKI Special Course on Supercavitating Flows. Brussels, Belgium: VKI, 2001: EN-010-04.

[10]PARISHEV E V. Pulsations of vertical cavities in ponderous fluid [J]. Uch Zap TsAGI, 1981, 12(3): 1-9.

[11]VASIN A D. The principle of independence of the cavity sections expansion (Logvinovich’s principle) as the basis for investigation on cavitation flows [C]∥VKI Special Course on Supercavitating Flows. Brussels, Belgium: VKI, 2001: RTO-EN-010(8).

[12]曹偉, 王聰, 魏英杰, 等. 自然超空泡形態特性的射彈實驗研究 [J]. 工程力學, 2006, 23(12): 175-187. CAO Wei, WANG Cong, WEI Yingjie, et al. High-speed projectile experimental investigations on the characteristics of natural supercavitation [J]. Engineering Mechanics, 2006, 23(12): 175-187.

[13]周素云, 施紅輝, 胡青青, 等. 水平超空泡發生裝置的研制及相關實驗研究 [J]. 浙江理工大學學報, 2013, 30(2): 218-223. ZHOU Suyun, SHI Honghui, HU Qingqing, et al. Development of horizontal supercavity generating facility and relevant experimental study [J]. Journal of Zhejiang Sci-Tech University, 2013, 30(2): 218-223.

[14]張學偉, 張亮, 于開平, 等. 自然超空泡形態穩定性的數值仿真 [J]. 彈道學報, 2009, 21(2): 103-106. ZHANG Xuewei, ZHANG Liang, YU Kaiping, et al. Numerical simulation of shape stability of natural supercavitation [J]. Journal of Ballistics, 2009, 21(2): 103-106.

[15]劉海旻, 張宇文, 弋輝. 空泡形態的公式計算與CFD仿真 [J]. 指揮控制與仿真, 2011, 33(6): 116-118. LIU Haimin, ZHANG Yuwen, YI Hui. Cavity form formula computation and CFD simulation [J]. Command Control & Simulation, 2011, 33(6): 116-118.

[16]施紅輝, 胡俊輝, 周浩磊. 完全超空泡出水的實驗研究及理論分析 [J]. 空氣動力學學報, 2014, 32(4): 544-550. SHI Honghui, HU Junhui, ZHOU Haolei. Experimental study and theoretical analysis of water exit of a supercavity [J]. Acta Aerodynamica Sinica, 2014, 32(4): 544-550.

[17]胡俊輝. 水下垂直發射的航行體在出水過程中超空泡的形成、潰滅及其與自由面相互作用的水動力學機理研究 [D]. 杭州: 浙江理工大學, 2014.

[18]袁緒龍, 張宇文, 劉樂華. 空泡外形測量與分析方法研究 [J]. 實驗力學, 2006, 21(2): 215-219. YUAN Xulong, ZHANG Yuwen, LIU Lehua. On methods of cavity profile measurement and analysis [J]. Journal of Experimental Mechanics, 2006, 21(2): 215-219.

(編輯 荊樹蓉)

Experimental Research on the Shape of Water-Exit Supercavity and the Effect of Froude Number

JIA Huixia,HU Junhui,SHI Honghui,CHEN Bo

(Department of Fluid Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The interreaction mechanism between the supercavitation and the free interface of the submarine-launched missiles or projectiles with supercavities has not been clearly understood. And the description about the supercavity shape in an unsteady flow with gravity also needs to be further investigated. An experimental study on underwater high-speed projectiles was carried out in a self-designed experimental facility. The water-exit process of projectiles and the shape change of supercavities were recorded by a high-speed camera. The size, contour, formation and collapse of the supercavities were measured and analyzed. The experiment data were compared with the theoretical formula and semi-empirical formula. The results show that under the studied conditions, the semi-empirical formula of Savchenko can be extended to the cavitation number less than 0.12. In addition, the experimental data are higher than the theoretical value given by Vasin considering the effect of gravity. A coefficient is added to modify the given formula. Furthermore, the experimental study shows that the shape of projectile head has great effect on the size of the formed supercavities. When the supercavities come into contact with the free surface, the supercavity diameter will be increased to a certain extent.

supercavitation; water-exit; high-speed projectiles; supercavity shape

2014-07-02。 作者簡介:賈會霞(1977—),女,博士,講師;施紅輝(通信作者),男,教授,博士生導師。 基金項目:浙江省自然科學基金資助項目(LQ13A020005,LQ13A020006,Z1110123)。

時間: 2014-12-18

網絡出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141218.1008.001.html

10.7652/xjtuxb201503012

O359

A

0253-987X(2015)03-0067-07