基于幅頻譜估計系統時域響應的改進方法研究

陳 翔 汪連棟 陳永光 曾勇虎 韓 慧 董 俊

（1.電子信息系統復雜電磁環境效應國家重點實驗室，河南 洛陽471003；2.北京跟蹤與通信技術研究所，北京100094）

引 言

現行標準及人們習慣中，一些電磁兼容測量結果常以幅頻曲線表征，如材料的屏蔽效能、濾波器的插入損耗、接收天線的頻域特性以及傳感器探頭的校正系數等等.在實驗條件受限，而人們又希望僅通過頻域測量結果估計系統的時域特性時，就需要采取一定的方法對忽略的相頻信息進行重構.可行的方法是，假設系統為最小（或最大）相位系統，根據Hilbert變換重構其相位信息［1-2］.雖然不是所有系統都滿足最小相位假設，但任何系統都可表示為一個最小相位系統和一個全通系統的級聯，而全通系統并不會改變傳輸信號的幅度特性，因此可在最小相位假設條件下對系統進行初步考察.

最小相位法陸續被引入到相關研究領域解決了各自面臨的實際問題，2000年，石立華等［3］提出使用最小相位系統模型，利用幅-頻曲線重構系統的相位信息，進而估計系統的時域響應，找到了一條系統的頻域指標到時域指標的轉換途徑.2004年，謝彥召等［4-5］根據最小相位原理，基于頻域幅度譜數據成功反演了高空核爆電磁脈沖和余（正）弦阻尼振蕩的時域波形，對于非最小相位信號，重建波形與原始波形有一定差異，但還是可以提供一些波形、累計能量、幅值量級的信息.2012年，曹景陽等［6］將傳感器視為滿足最小相位假設的信號傳輸系統，通過傳感器的修正系數計算了相頻特性，得到了系統的沖激響應，進而恢復了待測電磁脈沖的時域波形，解決了脈沖敏感度試驗中門限電平不易確定的難題.

以上常規的最小相位估計時域響應方法，在實現過程中由于反復使用快速傅里葉變換（Fast Fourier Transform，FFT）在時-頻域間轉換信號，會產生額外的數值誤差，此時必須仔細選擇FFT的相關參數，減小引入誤差.一些改進的處理方法是使用prony法［3］、最佳逼近元法［7］或者是濾波器建模［8］等對頻域傳遞函數進行參數化估計，得到系統的離散傳遞函數模型，由頻域參數模型估計系統的沖激響應.但是，prony法等參數建模方法也存在著一些的局限性［9］，如擬合精度差、所得極點不穩定、算法的收斂性特別依賴于初始值的選擇等.文獻［6］和文獻［7］的討論中還提到常規最小相位法對于高頻噪聲較為敏感，噪聲對重建效果影響較大.

為克服prony法等參數估計方法的不足，減小最小相位法對噪聲的敏感性，提出了一種將向量擬合法（Vector Fitting，VF）與最小相位法（Minimum-Phase，MP）相結合的由幅頻譜估計時域響應的改進方法（簡稱VF-MP方法）.首先給出VF-MP方法的基本思路，然后在介紹最小相位法與向量擬合基本原理的基礎上，以材料屏蔽效能測試為研究對象，使用材料屏蔽效能的仿真數據驗證VF-MP方法的可行性.

1 基本原理

1.1 最小相位法

在假定系統滿足最小相位的條件下，可通過Hilbert變換由系統的幅頻信息恢復相頻信息.利用FFT可以很方便地將數據在時域與頻域間轉換，也就可以使用Kolmogoroff方法（簡稱柯氏法）［10］求取幅度譜對應的最小相位序列，其基本流程如圖1所示.其中，Xc（n）為實倒譜）復倒譜，x（n）為最小相位序列.首先，對幅度譜取自然對數，然后用傅里葉逆變換（Inverse Fast Fourier Transform，IFFT）和FFT實現Hilbert變換，再取指數就可得x（n）的傅里葉變換X（ω），經IFFT后得到x（n）.

圖1 柯氏法求解最小相位序列

計算時需注意以下幾點：1）取對數后的幅度譜在進行IFFT之前，需對數據進行對稱延拓處理.2）使用FFT得到的實倒譜（K）是倒譜混疊后的偶數部分，需經頻率不變線性濾波從Xc（n）恢復.3）計算的在N很大時才是復倒譜的有效近似.

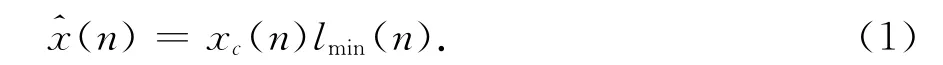
式中，lmin（n）＝2u（n）-δ（n）為加窗濾波函數.

柯氏法采用FFT算法，實現簡單、計算快速.但是當最小相位系統的零點比較靠近單位圓時，幅度譜的值接近于0，采用對數運算會產生大的誤差，可使用改進的柯氏法［10］，通過迭代估計來減小誤差.

1.2 向量擬合

如果直接使用圖1中得到的最小相位序列作為系統的時域模型，最后估計的結果可能受到高頻噪聲的影響.較好的處理方法是根據最小相位法重構的復頻域傳遞函數，選取一種模型對其進行參數估計.與一些常用的參數建模方法相比，B.Gustavsen提出的向量擬合法［11-12］，能夠對頻域測試數據進行穩定的有理函數逼近，已成功應用于電源系統、電路系統、天線等方面的建模中［13-15］.

復頻域的離散數據，可以由給定階次的兩個多項式比值的有理函數式來擬合為

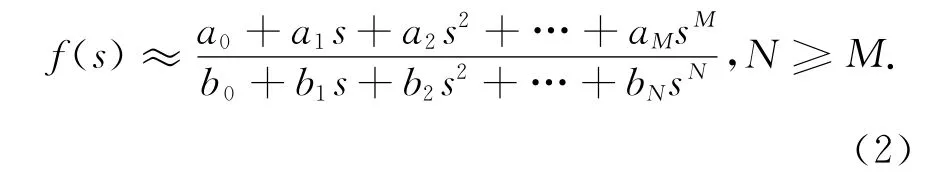
式中：a0，a1，…，aM和b0，b1，…，bN為待辨識的實系數；s＝jω.

假設有一組復頻域的采樣數據ωi、f（si），i＝1，…，N，將數據帶入式（4）可以得到形如Ax＝b的線性方程組.當階數較高、頻率較寬時將產生一個“病態”的方程組.這對于頻譜范圍寬、頻率上限可高達GHz以上的電磁脈沖估計來說，會產生嚴重的偏差，向量擬合法［11］通過將式（2）表示成式（3）的部分分式展開形式克服了這一缺點.

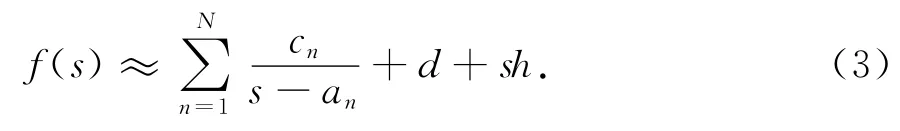
式中：cn是留數；an是實數或者共軛復數對的極點；d和h是實數.使用最小二乘法估計式（3）中的參數，分成極點辨識和留數辨識兩步實現，

引入輔助函數σ（s）

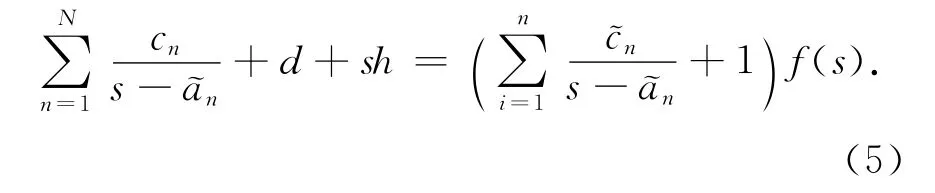
或者寫為

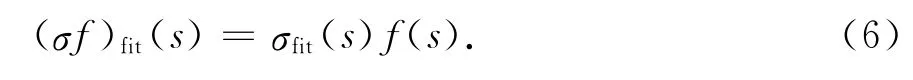
問題的求解就被轉化為線性問題，其中cn，d，h，~cn未知.根據給定的一組頻率點的采樣值，可將式（6）整理成線性方程組的形式

x未知，使用最小二乘法求解式（7）.

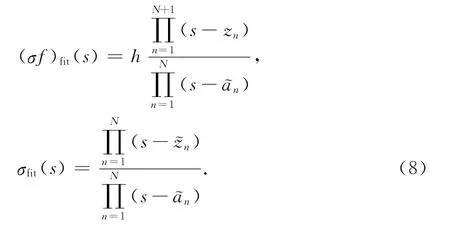
由式（8）可得

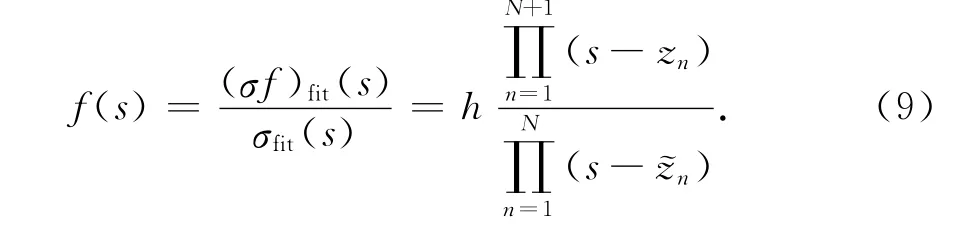
一次求解得到的極點往往不夠精確，將所得極點作為假定極點，重復式（4）到式（7）的步驟，進行迭代，得到更精確的極點.為了獲得更為精確的結果，根據式（3）的展開式計算留數.以上關于極點和留數的辨識，都只涉及到線性方程組的運算，方程系數矩陣的條件數一般也不會隨階數的提高增大，與其它方法相比向量擬合法更適用于高階或寬頻帶的有理函數擬合.

當曲線較為平滑時，僅使用實數形式的初始極點即可.當曲線有諧振峰時，初始極點應使用式（10）形式的復共軛極點形式，極點的頻率應該覆蓋測試的范圍.

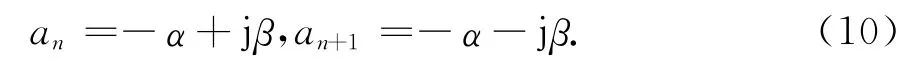
式中，α＝β／100.

1.3 VF-MP方法的基本流程

不考慮材料的磁飽和等非線性特性，將屏蔽體對電磁波的屏蔽近似為線性時不變系統.以電場屏蔽效能為研究對象，屏蔽體的電場屏蔽效能S（ω）與其傳遞函數H（ω）的關系可表示為式（11）.

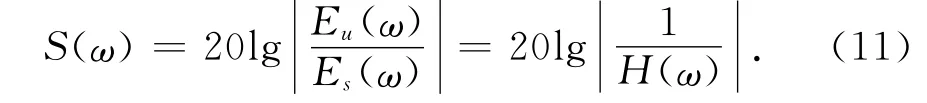
式中：ω為角頻率；Eu（ω）為未屏蔽的電場強度；Es（ω）為屏蔽后的電場強度.

傳遞函數的幅頻特性可寫為式（12）.

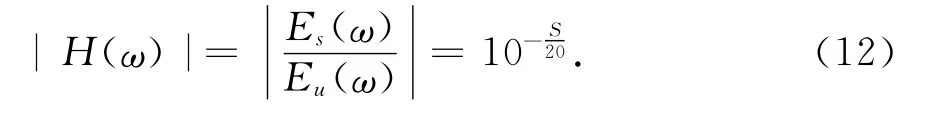
圖2為VF-MP方法的流程圖，即在使用最小相位法得到頻域傳遞函數之后，采用向量擬合法得到頻域傳遞函數的有理函數式參數模型，然后通過拉普拉斯逆變換得到屏蔽體的指數疊加形式的沖激響應函數，再與待估電磁脈沖直接在時域卷積，最終得到屏蔽體的電磁脈沖響應.

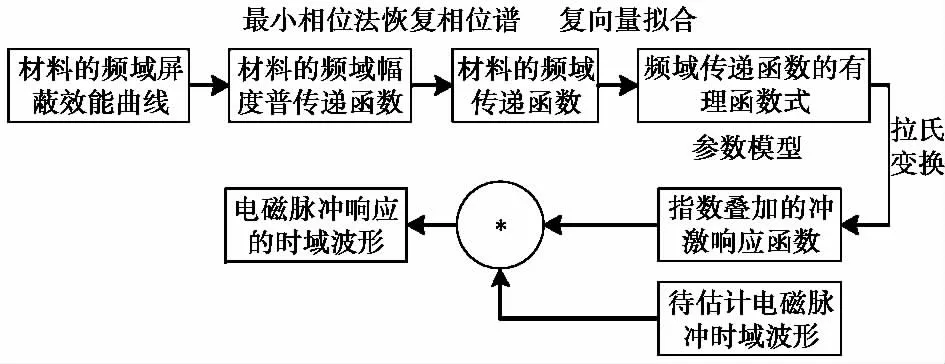
圖2 采用VF-MP方法的參數模型估計流程圖

使用向量擬合法對屏蔽體的電場傳遞函數H（jω）進行擬合后，可以將其表示為式（13）.

對式（13）進行拉普拉斯反變換得到屏蔽體沖激響應的雙指數疊加形式.

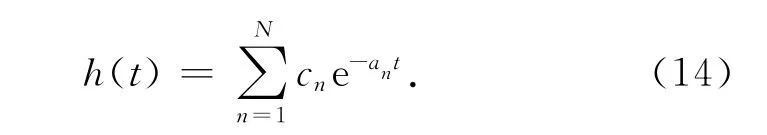
由式（14）和時域卷積的定義，采用梯形積分法可得到x（t）和h（t）的遞歸卷積式（15）.

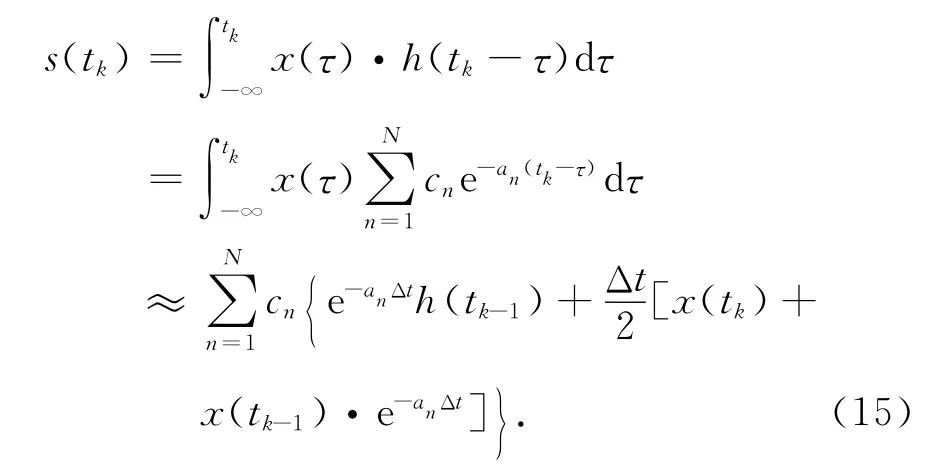
式中：Δt為采樣間隔；tk時刻的響應由tk-1時刻的響應和兩時刻激勵共同確定.

遞歸卷積算法可以縮短計算時間，與向量擬合法相結合還可以減少使用FFT和IFFT在時頻域間的轉換次數，克服了一些常規參數模型估計的局限性，減小了數值誤差.

2 平面材料仿真實驗驗證

以無限大平面材料的仿真數據為例，研究利用材料屏蔽效能的幅頻曲線估計其電磁脈沖響應.設置理想平面材料的厚度為1mm，相對介電常數和相對磁導率為1，電導率為1×103S／m，材料的理論屏蔽效能曲線如圖3（a）所示.圖3（b）為滿足IEC61000-4-4標準的入射電磁脈沖波形，使用雙指數函數擬合得到，峰值場強為50kV／m，修正系數為1.03，脈沖前后沿參數分別為4×107s-1和6×108s-1，使用CST（Computer Simulation Technology）軟件計算經材料衰減后的電磁脈沖波形（見圖4）.

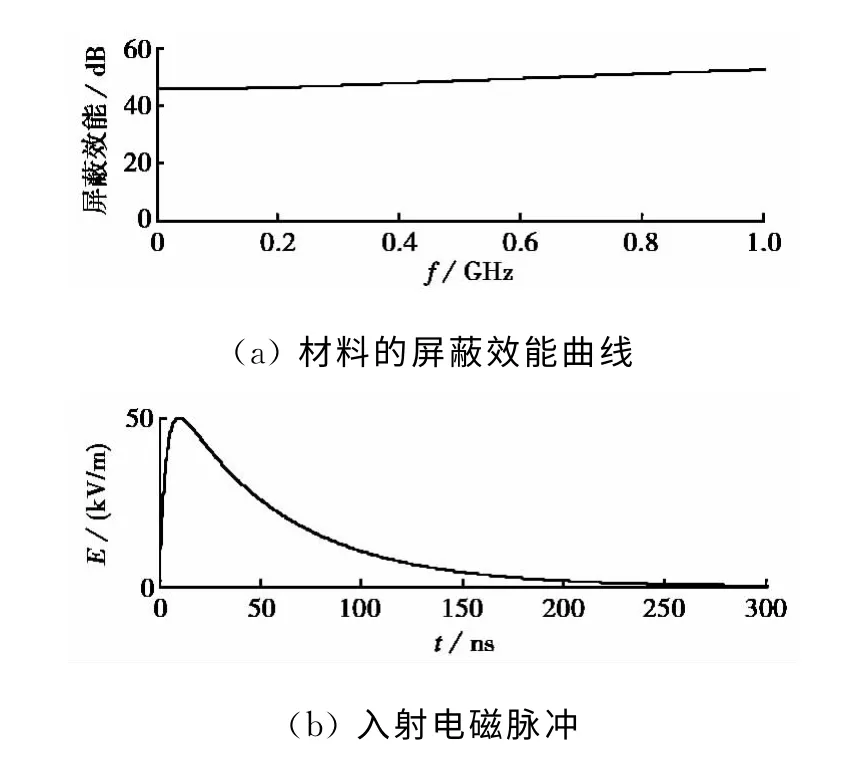
圖3 建模用仿真數據

使用常規最小相位法計算圖3（b）中透過材料后的脈沖波形，結果也列于圖4中.可見最小相位法估計的電磁脈沖響應波形與理論計算的波形非常接近.理想無限大平面材料的屏蔽行為可看作一個良好的線性系統，在沒有噪聲的情況下，僅依靠常規最小相位法即可很好地估計材料的電磁脈沖響應.

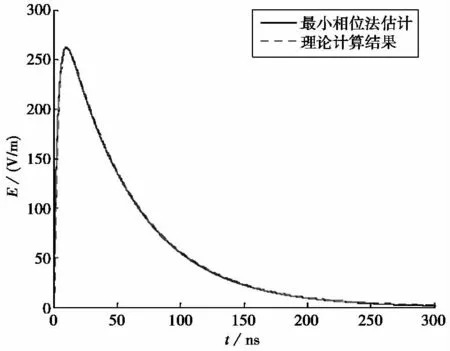
圖4 最小相位法估計的材料電磁脈沖響應

然而在實際測試中，數據會不可避免地遭受噪聲污染，屏蔽效能曲線不會像圖3（a）中那樣平滑.通過給屏蔽效能曲線疊加上不同程度的高斯白噪聲，來模擬實測頻域曲線，研究噪聲對最小相位法使用效果的影響.給圖3（a）中的屏蔽效能曲線疊加上平均值為0、標準差分別為其最大值2%和4%的噪聲.使用受噪聲污染的屏蔽效能曲線，采用常規最小相位法估計材料的電磁脈沖響應，在同一噪聲水平下一共計算了三次，結果如圖5所示.可看出當噪聲較大時，估計的時域波形與沒有噪聲污染時的波形相比，峰值誤差增大，脈沖的上升沿部分受噪聲的影響較小，但脈沖下降沿畸變嚴重；即使對同一水平的噪聲，由于每次疊加噪聲為隨機生成，所估計波形也有很大不同.

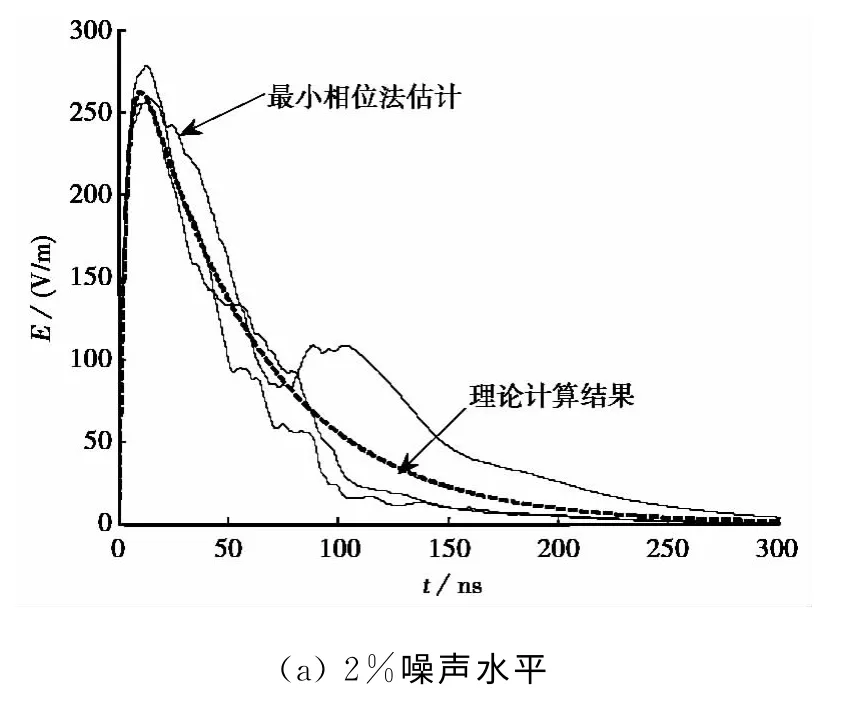
圖5 不同噪聲水平下常規最小相位法估計的波形

仍以疊加噪聲的屏蔽效能曲線為例，嘗試使用VF-MP方法估計材料的電磁脈沖響應.由于理想無限大平面材料的屏蔽是一個良好的線性系統，所需模型的階次較低，極點設置為實數即可.經試驗發現，當擬合階次為4時，進行5次迭代即可很好地擬合屏蔽效能傳遞函數曲線.使用4階模型、迭代5次，分別對幾組2%和4%噪聲水平下的數據進行擬合，結果均保持了很好的穩定性，并未因為每次疊加噪聲的隨機性而發生大的變化，圖6給出了2%噪聲水平下傳遞函數幅度譜的擬合結果.可預見，估計的材料電磁脈沖響應波形也會保持很好的重復性，不會如圖5中那樣有劇烈變化.

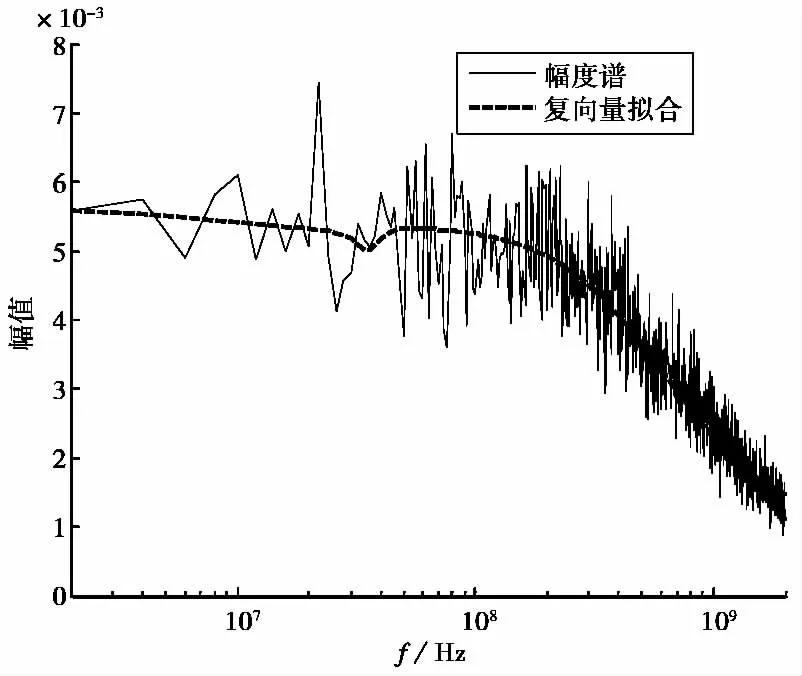
圖6 向量擬合法對傳遞函數幅頻曲線的擬合

使用式（15）給出的遞歸卷積公式直接與圖3（b）的時域波形卷積，即可得到材料的電磁脈沖響應，結果如圖7所示.可見采用VF-MP法估計的材料電磁脈沖響應波形，與理論計算的波形非常接近，受噪聲影響較小.

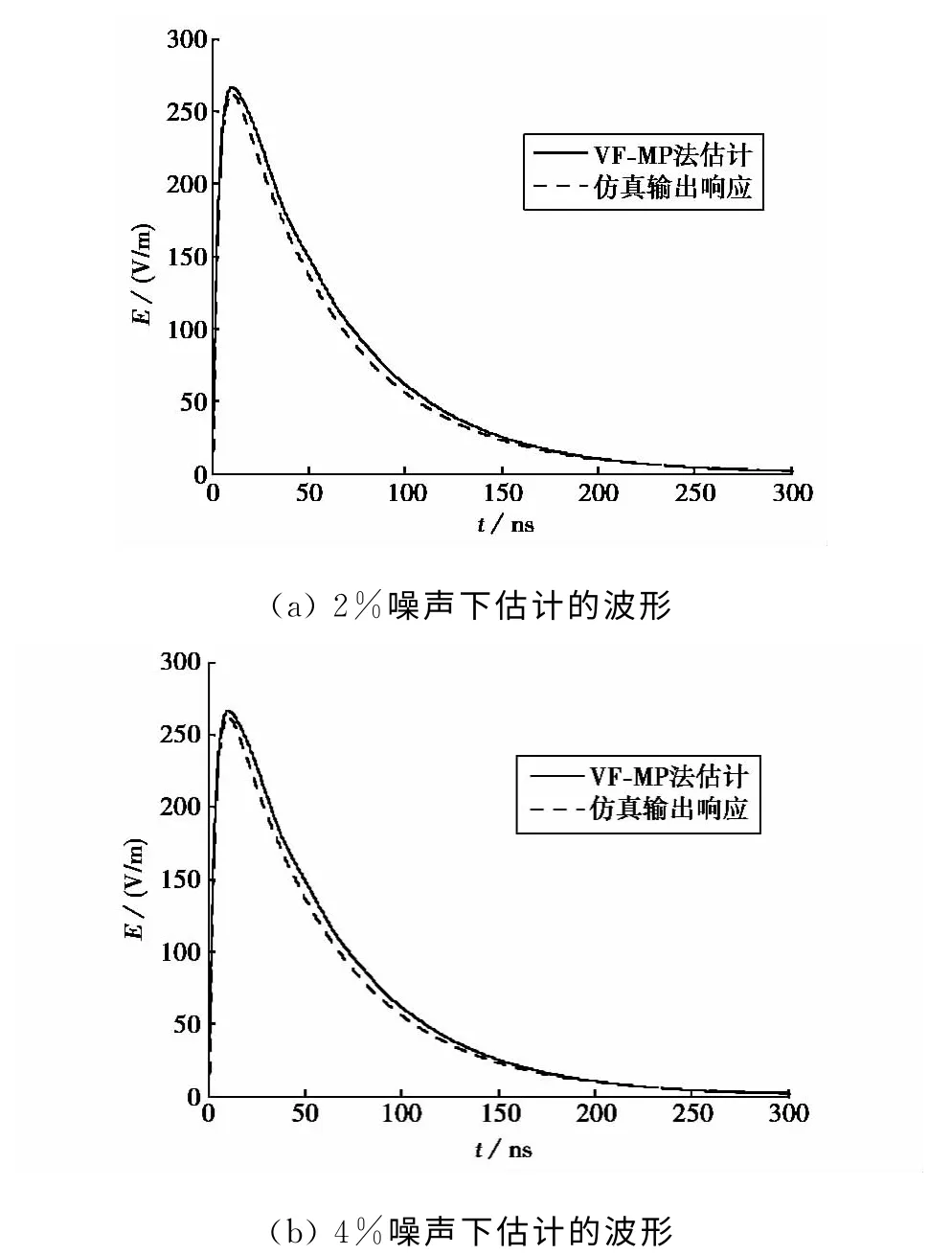
圖7 不同噪聲水平下VF-MP法估計的時域波形

3 暗箱窗口法仿真實驗驗證

繼續使用暗箱窗口法的仿真數據來檢驗VFMP方法，測試材料的電磁參數與上一節保持不變.仿真模型使用文獻［16］中的設置，箱體為1m×1m×1m的正方體，窗口尺寸為60cm×60cm，測試點A0位于窗口中心軸線上距窗口10cm處.圖8（a）為測得的材料對于垂直入射平面波的插入損耗曲線；圖8（b）為幅值1V／m、上升時間1ns、平頂保持47ns、下降時間4ns的方波脈沖激勵下，窗口未加載材料時A0點的時域波形.

根據圖8中的數據，使用VF-MP方法估計加載材料后A0點的時域波形，由于幅頻曲線不平滑，應使用復共軛極點和較高階次進行向量擬合.以均方誤差來衡量向量擬合法對傳遞函數的擬合效果，分別嘗試使用10階、20階、30階、40階模型，每一階次迭代20次，計算相應階次和迭代次數下的均方誤差.經試驗發現在階次為30、迭代10次時，模型的均方誤差較小，擬合精度已足夠好.由VF-MP方法估計的時域波形如圖9所示，可見VF-MP方法大致能夠估計出加載材料之后的時域波形，但與實際響應波形相比，峰值偏小，擬合度不夠高.使用VF-MP方法估計的材料峰值屏蔽效能為47.5dB，而根據CST軟件計算的結果為44.6dB，相差了大約3dB.這主要是因為暗箱窗口法測試比無限大平面材料情況要復雜得多，不滿足最小相位系統的假設.由于測試中窗口的存在，測得的脈沖不只受材料衰減的影響，窗口的截止波導作用同樣會改變電磁脈沖各頻率分量的相位，而且在箱體內還存在著些許諧振的影響，最終導致實際情況與最小相位假設不符.

圖8 建模用仿真數據

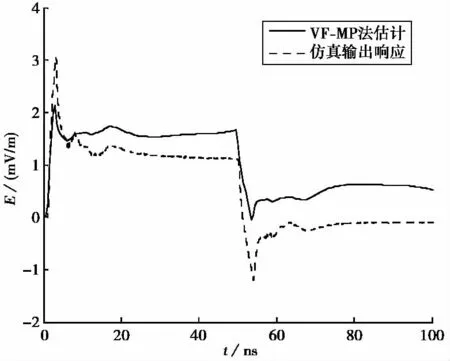
圖9 VF-MP法估計波形與仿真波形

4 結 論

采用向量擬合法與最小相位法相結合的VFMP方法是對常規最小相位法的有益補充，減小了因反復進行時頻轉換而產生的數值誤差，估計結果受噪聲影響小，重復性好.受最小相位假設的限制，對于不滿足最小相位近似的系統，估計結果會存在一定的偏差，但可用作前期的粗略估計.

［1］HAYES M H，LIM J S，OPPENHEIM A V.Signal reconstruction from phase or magnitude［J］.IEEE Transactions on Acoustics，Speech，Signal Processing，1980，28：672-680.

［2］TESCHE F M.On the use of Hibert transform for processing measure CW data［J］.IEEE Transactions on Electromagnetic Compatibility，1992，34（3）：259-266.

［3］石立華，周璧華，陳 彬，等.基于幅-頻曲線的系統時域響應特性評價方法［J］.電波科學學報，2000，15（4）：467-471.SHI Lihua，ZHOU Bihua，CHEN Bin，et al.Timedoamin characterization of a system based on the magnitude of its frequency response［J］.Chinese Journal of Radio Science，2000，15（4）：467-471.（in Chinese）

［4］謝彥召，王贊基，王群書，等.基于頻域幅度譜數據重建電磁脈沖時域波形［J］.強激光與粒子束，2004，16（3）：320-324.XIE Yanzhao，WANG Zanji，WANG Qunshu，et al.Reconstruction of electromagnetic pulse waveform based on the amplitude spectrum data［J］.High Power Laser and Particle Beams，2004，16（3）：320-324.（in Chinese）

［5］謝彥召，劉順坤，孫蓓云，等.電磁脈沖傳感器的時域和頻域標定方法及其等效性［J］.核電子學與探測技術，2004，24（4）：395-399.XIE Yanzhao，LIU Shunkun，SUN Beiyun，et al.Methodology of time-domain ＆frequency-domain calibration and equivalence for EMP sensor［J］.Nuclear Electronics ＆Detection Technology，2004，24（4）：395-399.（in Chinese）

［6］曹景陽，謝樹果，蘇東林.基于最小相位法重建電磁脈沖時域波形［J］.電波科學學報，2011，26（6）：1102-1106.CAO Jingyang，XIE Shuguo，SU Donglin.Application of minimum phase method in a pulse measurement［J］.Chinese Journal of Radio Science，2011，26（6）：1102-1106.（in Chinese）

［7］石立華，司 卿，張 琦，等.屏蔽室脈沖波屏蔽效能模型估計方法［J］.電波科學學報，2013，28（1）：125-129.SHI Lihua，SI Qing，ZHANG Qi，et al.Model estimation metohd for shielding effectiveness of shielding enclosure in pulse field［J］.Chinese Journal of Radio Science，2013，28（1）：125-129.（in Chinese）

［8］郭東義，石立華，郭曜華，等.基于頻響函數測量脈沖磁場屏蔽效能的新方法［J］.信息與電子工程，2010，8（1）：49-52.GUO Dongyi，SHI Lihua，GUO Yaohua，et al.Measurement for shielding effectiveness of pulsed magnetic field based on frequency response function［J］.Information and Electronic Engineering，2010，8（1）：49-52.（in Chinese）

［9］張 黎，李慶民，王 偉，等.用于傳遞函數參數辨識的改進復向量擬合法［J］.高電壓技術，2008，34（8）：1542-1546.ZHANG Li，LI Qingmin，WANG Wei，et al.Improved vector method for parameter identification of transfer functions［J］.High Voltage Engineering，2008，34（8）：1542-1546.（in Chinese）

［10］李衍達，常 迥.信號重構理論及其應用［M］.北京：清華大學出版社，1991：78-80.

［11］GUSTAVSEN B，SEMLYEN A.Rational approximation of frequency of frequency domain responses by vector fitting［J］.IEEE Transactions on Power Delivery，1999，14（3）：1052-1061.

［12］GUSTAVSEN B.Improving the pole relocating properties of vector fitting［J］.IEEE Transaction on Power Delivery，2006，21（3）：1587-1592.

［13］DESCHRIJVER D，MROZOWSKI M，DHAENE T，et al.Macromodeling of multiport systems using a fast implementation of the vector fitting method［J］.IEEE Microwave and Wireless Components Letters，2008，18（6）：383-385.

［14］郭 劍，鄒 軍，何金良，等.基于Vector Fitting的金屬薄殼電磁脈沖屏蔽效能的計算［J］.清華大學學報：自然科學版，2004，44（10）：1302-1305.GUO Jian，ZOU Jun，HE Jinliang，et al.Evaluation of EMP shielding effectiveness for metallic sheels based on the vector fitting method［J］.J Tsinghua University：Science and Technology，2004，44（10）：1302-1305.（in Chinese）

［15］魏 琰，郭裕順.基于向量擬合法的多端口網絡函數有理逼近及其瞬態分析［J］.電路與系統學報，2008，13（1）：67-72.WEI Yan，GUO Yushun.Rational approximation of multiport network functions by the vector fitting algorithm［J］.Journal of Circuits and Systems，2008，13（1）：67-72.（in Chinese）

［16］陳 翔，陳永光，魏 明，等.基于屏蔽暗箱窗口法的材料電磁脈沖屏蔽效能時域測試［J］.高電壓技術，2013，39（3）：668-674.CHEN Xiang，CHEN Yongguang，WEI Ming，et al.Time-domain test for electromagnetic pulse shielding effectiveness of materials based on the method of windowed semi-anechonic box［J］.High Voltage Engineering，2013，39（3）：668-674.（in Chinese）