灰色變權組合模型的貨車車輪踏面磨耗預測

?

灰色變權組合模型的貨車車輪踏面磨耗預測

李瀅1,湯旻安1,2,谷寶慧1

(1. 蘭州交通大學 自動化與電氣工程學院，甘肅 蘭州 730070;

2． 蘭州理工大學 機電工程學院，甘肅 蘭州 730050)

摘要:為探討變權組合模型在貨運專線車輪踏面磨耗趨勢預測中的應用，采用基于灰色新息GM(1,1)模型、灰色離散GM(1,1)模型和指數平滑模型為一體的變權組合方法研究貨運專線車輪踏面隨走行公里的磨耗趨勢，并與各單項模型預測結果和定權組合預測結果作對比，研究結果表明：應用組合方法比單純應用單項預測模型方法更合理，預測結果更可靠，且變權組合預測模型優于定權組合預測模型，預測精度較高。本文所提出的變權組合預測方法能夠很好地預測貨運專線上車輪踏面的磨耗趨勢，是一種研究運輸專線上車輛輪對維護決策的有效方法。

關鍵詞：車輛工程；貨運專線；車輪踏面磨耗；組合預測；變權組合模型

Forecast research on trucks wheel tread wear based

on grey changeable weight combination model

LI Ying1，TANG Minan1,2，GU Baohui1

(1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;

2. School of Mechanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

Abstract:In order to discuss the application of changeable weight combination forecasting model in wheel tread wear forecasting of freight line, the changeable weight combination forecasting method based on new information GM (1,1) model, discrete GM(1,1) model and exponential smoothing model was utilized to analyze wheel tread wear volumes along with the change of running distances. Subsequently, the results obtained in this paper were compared with the prediction ones with single models and the fixed weight combination prediction ones. The results show that combination forecasting method is more reasonable than purely single forecasting method and the solutions are more reliable. The changeable weight combination forecasting mode is better than fixed weight combination model and has a higher prediction accuracy. Therefore, an effective forecast method is giving for accurately predicting the wear volumes and could be a feasible solution to freight line vehicle wheel maintenance and decision.Key words: vehicle engineering; freight line; wheel tread wear; combination forecasting; changeable weight combination forecast model

隨著我國軌道交通的迅速發展，對機車車輛的安全性提出了更高的要求。而車輪作為列車的關鍵走行部件，其技術狀態的好壞直接關系到行車安全。其中，車輪磨耗是影響列車安全平穩運行的重要因素之一。機車向著高速、重載、高密度的方向發展加速了車輪的磨耗，而因磨耗和不當維修造成的換輪比例逐年增高，大大增加了運營成本。因而，實現車輪磨耗趨勢的預測，不僅可預先消除事故隱患，保證行車安全的同時還可作為維修管理部門進行維護的參考，增加輪對的使用壽命，降低運營成本。

在機車車輛運用和發展過程中，鐵路車輛的車輪磨耗問題一直是主要研究內容之一。它涉及到鐵路運輸的經濟性和安全性，國內外學者對此進行了深入研究[1-6]，提出了許多車輪磨耗模型，并結合車輛-軌道動力學模型將其應用到車輪磨耗仿真預測中。丁軍君等[7]以C80型貨車為例，基于FASTSIM 算法和Zobory踏面磨耗模型，對重載貨車車輪磨耗建立車輛動力學模型進行了仿真分析。羅仁等[8]建立車輛多體系統動力學和車輪磨耗耦合模型，研究了高速列車車輪磨耗問題，指出通過仿真方法預測車輪型面的磨耗可為高速列車的安全可靠運行提供指導。王凌等[9]根據廣州地鐵輪對的實際磨耗數據，給出一種數據驅動模型，并在該模型基礎上用蒙特卡洛仿真方法實現了輪對鏇修的策略優化。李亨利等[10]運用多體動力學方法分析重載坡道制動的車輛動力學行為及對輪軌磨耗的研究。DIRKS等[11]用Achard磨耗模型、安定理論和損傷函數預測車輪型面的磨耗和滾動接觸疲勞，并且分析了車輪滾動接觸疲勞損傷的影響。丁軍君等[12-13]從不同角度對車輪的磨耗壽命預測做了研究分析。上述車輪磨耗預測的研究大都以磨耗模型的發展及車輛-軌道動力學的仿真預測研究居多，而本文提出一種從車輪磨耗量隨時間變化的時間序列這個綜合灰變量本身尋找有用信息的思想來研究車輪磨耗預測問題。由于車輪磨耗是受載荷、速度、軌道狀態、線路運量以及氣候條件等眾多因素影響的復雜系統，存在許多不確定的隨機變量，而灰色模型和指數平滑法預測模型不用定量研究復雜系統內部因素及其之間的相互聯系，僅從時間序列這個綜合灰變量本身尋找有用信息[14]。因此，本文從運籌學的角度出發，構建了灰色新息GM(1,1)模型、灰色離散GM(1,1)模型和指數平滑模型為一體的定權組合模型和變權組合模型研究貨運專線上的車輪踏面磨耗趨勢，并通過對模型的準確度度量，驗證了變權組合預測方法在車輪踏面磨耗預測中的有效性。

1單項預測模型

1.1新息GM(1,1)預測模型

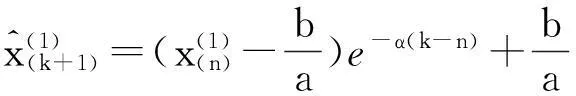
k=1,2,3,…n。

(1)

還原值為：

(2)

1.2離散GM(1,1)預測模型

對于非負離散數據序列，其一次累加生成序列是單調遞增并呈現指數變化趨勢，因此對離散點序列優先選擇離散GM(1,1)模型進行指數擬合就充分應用了原始數據的信息，為正確預測提供了保證。

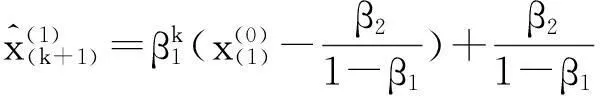
k=1,2,…n-1。

(3)

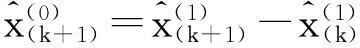
k=1,2,3,…n-1。

(4)

1.3指數平滑預測模型

指數平滑法認為時間序列的態勢具有連續性或穩定性，因而可以合理地順勢延伸。不同次數的指數平滑法預測精度不同。根據實際車輪磨耗變化數據，應用SPSS分析軟件對磨耗數據做回歸分析，如果呈現水平趨勢時，可用一次指數平滑值作為預測值；呈現線性趨勢時，應使用二次指數平滑值；如果具有二次曲線趨勢時則應使用三次指數平滑值。

指數平滑法最關鍵的是初始值和平滑系數的選取。初始值具體根據樣本數據的多少來確定，而對平滑系數α的選取，如果數據序列呈較平穩的水平趨勢，α宜取(0.1～0.3)，如果數據有大波動，α宜取(0.3～0.6)，而有上升或下降的斜坡趨勢時，α宜取(0.6～0.8)，以追蹤近期數據的變化。本文在遵循指數平滑法“厚近薄遠”[15]的原則之下，先根據數據序列波動的大小大概確定一個取值范圍再以均方誤差最小為準則選取平滑系數。

2組合預測模型

單項預測方法簡單、易操作，能從不同角度反映信息特征，但存在方法適用范圍有限、反映信息不全面等缺點。如果在預測過程中僅因為某個模型預測誤差大而將其舍棄，則可能造成有用信息的丟失。組合模型是通過一定的方法將2個或多個方法結合起來構建的一個新模型，可綜合利用各單項預測方法的有用信息，能一定程度的克服單項預測的缺陷，提高預測精度[16]。根據所組合的各方法的含權量，又可分為定權組合和變權組合兩種。變權組合能及時改變各組合方法的權重，跟蹤反映事物實際的變化，有效彌補了定權組合在這方面的缺陷。但是由于車輪磨耗過程的復雜性，決定了用單一預測方法無法全面提高計算、預測和決策的精度及可靠性。因此本文選取3種單項預測方法，建立車輪踏面磨耗量的定權和變權組合模型，然后將變權組合模型預測結果分別與各單項模型和定權組合模型結果進行比較，結果驗證了變權組合模型在車輪踏面磨耗趨勢預測中的合理性和優越性。預測結果對于維修部門制定合理的維修決策計劃，提高維修率，減少維修成本，增加車輪使用壽命具有一定實用意義。

2.1熵值法的定權組合權系數的確定

組合預測的核心問題就是如何求出組合預測加權平均系數，使組合模型更加有效地提高預測精度。本節利用信息熵值的概念，根據各單項預測方法預測誤差序列的變異程度，計算出組合預測加權平均系數。

用熵值法確定組合預測加權系數的步驟如下[17]：

(1)將各單項預測方法的相對誤差序列歸一化

(2)計算第i種單項預測方法相對誤差的熵值

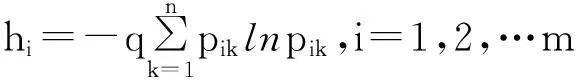
(3)計算第i種預測方法的相對誤差序列的變異程度系數

第i種預測方法預測相對誤差序列的變異程度系數di為：di=1-hi,i=1,2,…m。

(4)計算各種預測方法的加權系數

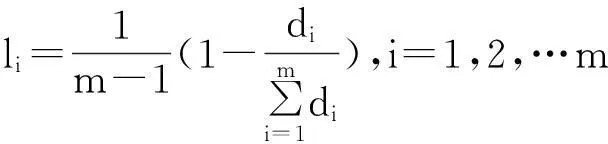
(5)計算組合預測值

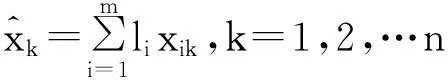
(5)

2.2變權組合預測方法及權系數的確定

變權組合預測方法是基于多種預測方法的組合預測方法，其關鍵問題在于變權系數的確定。由于權系數是隨時間變化的函數，所以確定起來相對有困難。首先建立樣本點的組合預測優化模型，求出各單項預測模型在各樣本點的組合權系數，再根據這些權系數確定各預測方法中預測時點的組合權系數[18]。

(6)

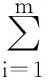
變權樣本點期權系數的確定采用絕對誤差法：

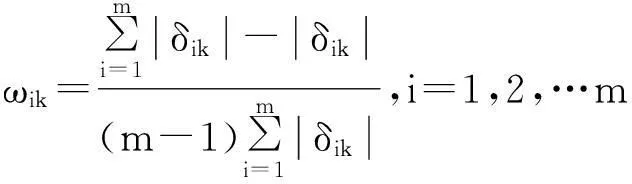
k=1,2,…n.

(7)

變權預測時點權系數的確定：

利用公式(7)得到的都是過去的權重值，而對將來值進行預測必須確定預測時點(k=n+1,n+2,…)的組合權重，即ωi,n+j(i=1,2,…m,j=1,2,…)。文獻[19]采用不同的方法討論了預測時點權系數的確定。本文用n+j時刻前n期的變權系數的平均值來代替n+j時刻的權重。即：

當j=1時，令

(8)

當j=2,3,…時，則

(9)

2.3組合預測模型評價指標

各模型預測的精確性與預測誤差密切相關，為反映組合預測效果的好壞，用均方根誤差、平均相對誤差和灰色關聯度度量組合預測模型的準確度。

(1)均方根誤差(MSE)：

(2)平均相對誤差(MAPE)：

(3)灰色關聯度(γ0i)：

3變權組合預測實例分析

車輪踏面磨耗作為車輪鏇修的度量值之一，其磨耗程度直接關系到車輪的鏇修時機和列車的運行安全。因而建立車輪踏面磨耗的灰色預測模型預測其未來的發展狀態具有重要的現實意義。為驗證本文所提方法的有效性，選取大秦鐵路線上運行的貨車車輪在一個段修期內的2組車輪踏面磨耗數據建立3種單項預測模型，并構建車輪踏面磨耗變化趨勢的變權組合預測模型，將其預測結果與定權組合模型和各單項模型結果進行比較。其中，通過SPSS軟件對2組原始數據的回歸分析發現數據序列呈線性趨勢的擬合程度較高，因此選取二次指數平滑模型作為一個單項模型。由于樣本數據具有明顯的增長趨勢，初值對預測結果影響較小，因而取序列第一期數據值作為初值。α分別取0.6，0.7和0.8進行試計算，當α=0.8時，均方誤差均最小。2組數據的預測結果與組合預測模型的性能比較見表1和表2所示。

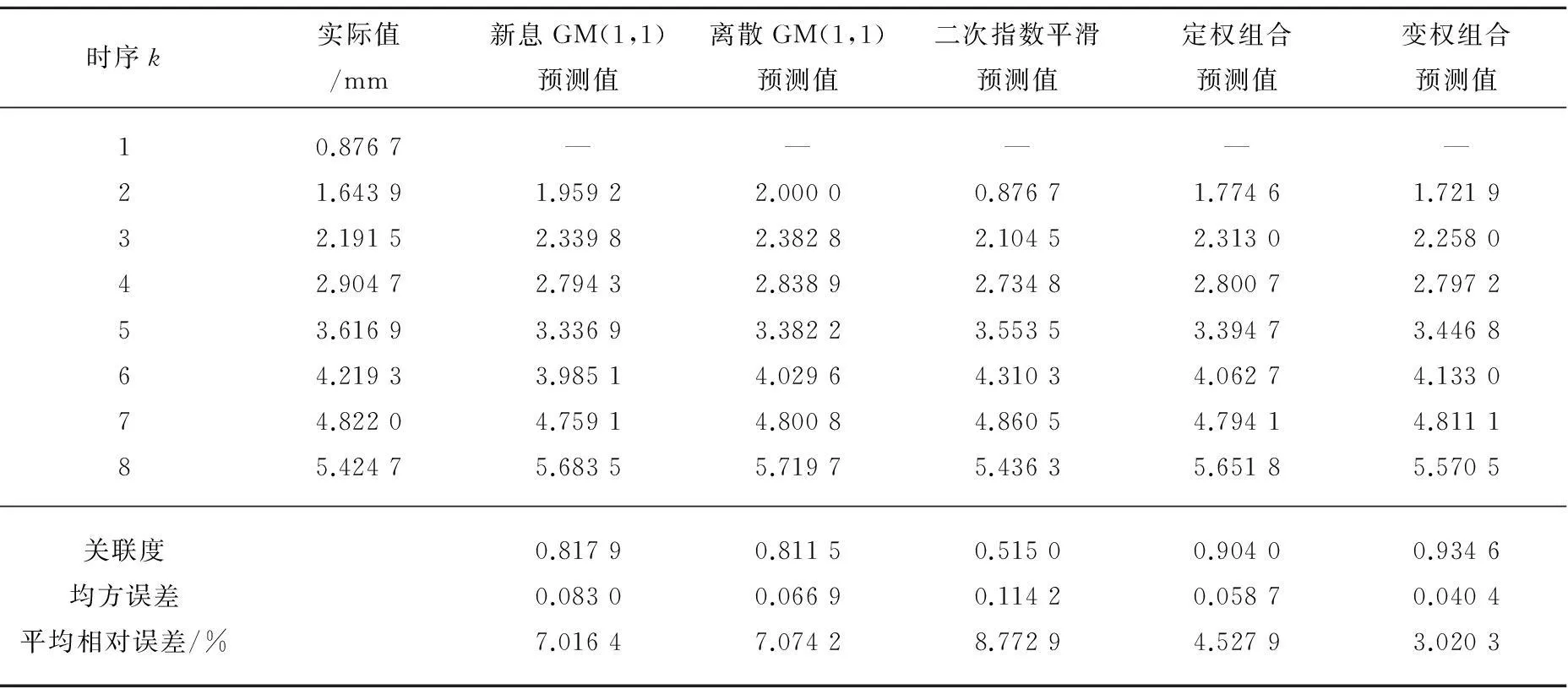
表1　第1組數據預測結果比較

表2　第2組數據預測結果比較

從上述表1和表2中可以看出，基于組合模型的預測結果從均方誤差、平均相對誤差和關聯度3方面均優于各單項模型的預測效果。這是由于組合模型綜合利用了各單項模型提供的有效信息，平衡了各單項模型之間的優缺點，弱化了各單項模型建模分析的局限性，實現各模型間的優勢互補，從整體上提高了模型預測的合理性和適應性。而變權組合預測模型的均方誤差和平均相對誤差均低于定權組合模型，同時其預測結果與實際數據序列的關聯程度最高，說明該模型預測的結果與實際數據更加接近，精度優于定權組合預測模型。

最后選取第2組數列中的后2個數據4.756 6和5.415 8做變權組合模型可靠性檢驗。依據公式(8)及公式(9)計算得到預測時點的權系數。計算當k=9和k=10時刻的權系數如表3所示。其預測值分別為4.760 4 mm和5.497 8 mm，預測精度均在98%以上，進一步驗證了變權組合模型更可靠。

表3　預測時點權重系數

灰色新息GM(1,1)模型和灰色離散GM(1,1)模型對“小樣本”，“貧信息”的不確定系統中“部分”已知信息的生成、開發挖掘出蘊含在系統觀測數據中的重要信息，實現了對車輪磨耗趨勢的正確描述和認識。接著再將兩模型預測結果與指數平滑模型的預測結果相組合，構建了可動態調整權系數的變權組合模型，從而提高了組合預測結果的合理性和可信度。

4結論

1) 分別采用3種預測模型對車輪踏面隨走行公里的磨耗量進行了預測，并構建了定權和變權組合預測模型。通過比較可知，組合預測模型從整體上具有比單個模型較優的特點。

2) 變權組合預測模型相對于定權預測模型來說，由于能夠隨時序動態地調整3種單項預測模型的權系數，使預測結果更接近實際，因而具有比定權組合模型更高的預測精度，增加了預測的可信度。

3) 依據本方法預測的磨耗數據，維修管理部門可結合車輪的段修或運用限度，為車輛輪對的維修、更換提供科學有效的參考。該方法可對鐵路運輸專線或在固定線路上運行的城市軌道車輛的車輪磨耗狀態進行及時控制，同時也為車輪的狀態修提供了一種新思路。

參考文獻：

[1] Arizon J D, Verlindeno, Dehombreux P. Prediction of wheel wear in urban railway transport comparison of existing models [J]. Vehicle System Dynamics, 2007, 45(9): 849-874.

[2] MAGEL E, KALOUSEK J, CALDWELL R. A numerical simulation of wheel wear[J]. Wear, 2005, 258: 1245-1254.

[3] Roger Enblom, Mats Berg. Impact of non-elliptic contact modeling in wheel wears simulation[J]. Wear, 2008, 265: 1532-1541.

[4] Roger Enblom, Mats Berg. Simulation of railway wheel profile development due to wear-influence of disc braking and contact environment[J]. Wear, 2005, 258: 1055-1063.

[5] 丁軍君, 黃運華, 李芾. 地鐵車輛車輪磨耗仿真研究[J].城市軌道交通研究,2013(10):73-77.

DING Junjun, HUANG Yunhua, LI Fu. Simulation and study of metro vehicle Wheel wear[J]. Urban Mass Transit, 2013(10): 73-77.

[6] 胡海濱, 呂可維, 邵文東, 等. 大秦鐵路貨車車輪磨耗問題的調查與研究[J]. 鐵道學報，2010，32(1)：30-37.

HU Haibin, Lü Kewei, SHAO Wendong,et al. Research on wheel wear of freight cars on datong-qinhuangdao railway line[J]. Journal of the China Railway Society, 2010, 32(1): 30-37.

[7] 丁軍君, 孫樹磊, 李芾,等. 重載貨車車輪磨耗仿真[J]. 交通運輸工程學報, 2011, 11(4):56-60.

DING Junjun, SUN Shulei, LI Fu, et al. Simulation of wheel wear for heavy haul freight car[J]. Journal of Traffic and Transportation Engineering, 2011, 11(4):56-60.

[8] 羅仁, 曾京, 戴煥云, 等. 高速列車車輪磨耗預測仿真[J]. 摩擦學學報, 2009, 29(6): 551-558.

LUO Ren, ZENG Jing, DAI Huanyun, et al. Simulation wheel wear prediction of high-speed train[J]. Tribology, 2009, 29(6): 551-558.

[9] 王凌, 員華, 那文波, 等. 基于磨耗數據驅動模型的輪對鏇修策略優化和剩余壽命預報[J]. 系統工程理論與實踐, 2011, 31(6): 1143-1152.

WANG Ling, YUAN Hua, NA Wenbo,et al. Optimization of the re-profiling strategy and remaining useful life prediction of wheels based on a data-driven wear model[J]. Systems Engineering - Theory & Practice, 2011, 31(6): 1143-1152.

[10] 李亨利, 李芾, 付茂海,等. 重載貨車坡道制動動力學及輪軌磨耗研究[J]. 鐵道科學與工程學報, 2014, 11(3): 60-64.

LI Hengli, LI Fu, FU Maohai,et al. Study on the braking dynamics and wheel/rail wear for the heavy haul trucks on ramp lines[J]. Journal of Railway Science and Engineering, 2014, 11(3): 60-64.

[11] Dirks B, Enblom R. Prediction model for wheel profile wear and rolling contact fatigue[J]. Wear, 2011, 271: 210-217.

[12] 丁軍君, 李芾, 周張義, 等. 基于車輪磨耗壽命預測的軌道參數研究[J]. 鐵道科學與工程學報, 2013, 10(4): 13-18.

DING Junjn, LI Fu, ZHOU Zhangyi, et al. Parametric study of the railway based on wheel wear lifetime prediction[J]. Journal of Railway Science and Engineering, 2013, 10(4): 13-18.

[13] 陶功權, 李霞, 鄧永果,等. 基于車輛橫向運動穩定性的車輪磨耗壽命預測[J]. 機械工程學報, 2013, 49(10): 28-34.

TAO Gongquan, LI Xia, DENG Tiesong, et al. Wheel wear life prediction based on lateral motion stability of vehicle system[J]. Journal of Mechanical Engineering, 2013, 49(10): 28-34.

[14] 徐建新, 嚴勇, 嚴富海. 指數平滑法在典型城市GDP預測中的應用[J]. 水利科技與經濟，2008，14(7)：551-554.

XU Jianxin, YAN Yong, YAN Fuhai. The application of exponential smoothing model in GDP prediction of typical city[J]. Water Conservancy Science and Technology and Economy, 2008, 14(7): 551-554.

[15] 諶小麗, 陳景雅, 王坤. 基于指數平滑法對我國私家車保有量的預測[J]. 華東交通大學學報，2013，30(1)：58-62.

ZHAN Xiaoli, CHEN Jinya, WANG Kun. Forecast of china private car ownership based on the exponential smoothing[J]. Journal of East China Jiaotong University, 2013, 30(1): 58-62.

[16] 王永剛，鄭紅運. 基于最優變權組合模型的航空運輸事故征候預測[J]. 中國安全科學學報，2013，23(4)：26-31.

WANG Yonggang, ZHENG Hongyun. Prediction of air transportation incidents based on combined model with optimal variable weight[J]. China Safety Science Journal, 2013, 23(4): 26-31.

[17] 陳華友. 組合預測方法有效性理論及其應用[M]. 北京：科學出版社，2008:51-52.

CHEN Huayou. The effectiveness of combination forecasting method theory and its application[M].Beijing:Science Press,2008:51-52.

[18] 崔巍, 王新民, 楊策. 變權組合預測模型在滑坡預測中的應用[J]. 吉林大學學報(信息科學版)，2010，28(2)：172-176.

CUI Wei, WANG Xinmin, YANG Ce. Application of changeable weight combination forecasting model to landslide prediction[J]. Journal of Jilin University (Information Science Edition), 2010, 28(2): 172-176.

[19] 王豐效. 基于變權GM(1,1)組合模型的喀什GDP預測[J]. 數學的實踐與認識，2013，43(24)：147-151.

WANG Fengxiao. Forecast on GDP of kashi region based on changeable weight combination forecast model[J]. Mathematics in Practice and Theory, 2013, 43(24): 147-151.

中圖分類號：U279.5

文獻標志碼：A

文章編號：1672-7029(2015)01-0160-06

通訊作者：湯旻安(1973-)，男，陜西勉縣人，副教授，博士，從事交通信息工程及控制，智能交通方向的研究;E-mail：tangminan@yahoo.com

基金項目：國家自然科學基金資助項目(61263004);甘肅省科技支撐計劃資助項目(090GKCA009，1304GKCA023);蘭州市科技攻關計劃資助項目(2013-4-18)

*收稿日期：2014-07-21