論流量影響線法參數誤差對計算流量的影響

?

論流量影響線法參數誤差對計算流量的影響

張洪翠1, 文雨松2

(1. 湖北省路橋集團有限公司,湖北 武漢 430056;

2. 中南大學 土木工程學院，湖南 長沙 410075)

摘要:使用單參數分析法、通過VB編程計算，解決流量影響線法各參數測量精度要求的問題，得到“標定洪水高程”、糙率系數和雨量系列的誤差對計算流量精度影響較大,其他參數影響較小的結論。如果將前三者測量誤差控制在5%以內，其他參數控制在10%以內，可以保證流量影響線法的精度。該結論可供橋涵水文勘測參考，有利于提高流量影響線法的計算精度,并提高經濟效益。

關鍵詞：流量影響線法；計算流量；測量參數；精度

設計流量(或檢定流量)是橋梁設計和橋梁維護的重要參數。計算流量的方法有很多，如依據流量觀測值的數理統計方法；依據雨量觀測值的經驗公式法、推理公式法、鐵路設計院法等[1-2]。最近出現的流量影響線法也是一種依據雨量觀測值的設計流量計算方法，它適用于中小橋涵的流量計算，因為這種方法不需要測量流域面積等外業資料而被廣泛關注[3]。流量影響線法的依據參數是雨量、漲水歷時、退水歷時、河道平均流速等。這些參數的準確度對設計流量或檢定流量影響程度及如何控制這種影響，因而成為橋涵水文工作者特別關心的事情，本文就此做出了分析和研究，其結論可供橋涵水文勘測參考[4]。

1流量影響線法簡介

1.1流量影響線法的基本原理

流量影響線法將單位時段內的降雨量Ri看成列車軸重Pi，將橋位漲水歷時t1看成簡支梁應力計算點到左支座的距離L1, 將橋位退水歷時t2看成簡支梁應力計算點到右支座的距離L2。這樣利用雨量Ri求流量Q的水文問題，就變成了利用簡支梁應力影響線加載求應力的力學問題[3]。

流量影響線法的計算如下，加載過程見圖1。

(1)

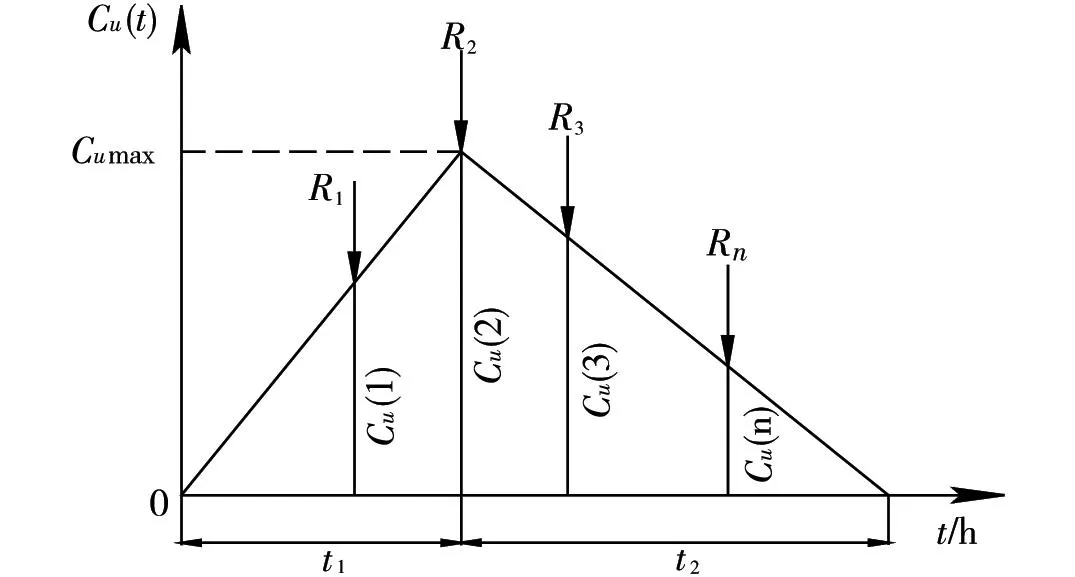
圖1　流量影響線加載示意圖Fig.1 Loading schematic diagram of flow influence line

1.2流量影響線法的標定

由結構力學可知，使用簡支梁應力影響線前，需要確定影響線的最大豎標Ymax。可以根據簡支梁的截面模量等參數計算結構力學中影響線的最大豎標Ymax，這是理論標定法。但最常用的方法是將一臺機車置于橋梁上，實測其最大應力，然后反算得到Ymax，這是實驗標定法。

同樣可以利用實驗法確定流量影響線的最大豎標Cumax。

取一次洪水為標定洪水，可以實測這次洪水的最大流量Qb，同時實測引發這次洪水的雨量系列R1,R2…Ri…Rn。

假定式(1)中的流量影響線峰值Cumax=1，將R1,R2…Ri…Rn當作移動荷載系列，在流量影響線上加載，按式(1)，可以計算出Qb′。

流量影響線峰值的標定值如下:

(2)

1.3利用流量影響線計算設計流量或檢定流量

若式(1)中雨量系列為設計頻率或檢定頻率對應的暴雨量系列，并利用流量影響線峰值的標定值Cumax，就可以確定設計流量(或檢定流量)Q[5]。

2流量影響線法的參數

2.1漲水歷時t1

流量影響線法計算漲水歷時t1，本著計算過程簡單、計算結果可靠的原則，采用下式進行計算[2]：

(3)

式中：t1為漲水歷時，h；L為流域中心到橋址的距離，km；V為沿流程平均流速，m/s。

2.2退水歷時t2

漲水歷時t1確定后，退水歷時t2借助漲、退水歷時之比t1∶t2確定。通過對瞬時單位線和廣東省綜合單位線簡化分析，結合中小流域的水文特性，并以廣西壯族自治區區流域實測資料作參照，制定了中小流域漲、退水歷時之比t1∶t2的選取標準(詳見參考文獻[3])：對于山區陡峭、植被很差的小流域，可取t1∶t2=1∶3； 平原區坡度較緩、流速較慢、植被較好的中等大小流域，可取t1∶t2=1∶1.5[3]。

2.3雨量荷載R

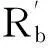
2.3標定流量Qb

確定Qb最好的方法是現場實測。

對于均勻穩定流河段，可以根據標定洪水在河岸或其他參照物上留下的水痕高程Hs按滿寧公式確定[7]，單式斷面流量計算如下：

(4)

式中：Qb為流量，(m3/s)；n為糙率；ω為過水斷面面積，m2；I為橋前水面坡度，rad；χ為濕周，m。

復式斷面流量計算如下：

(5)

式中：ni為河床斷面各部分糙率；ωi為河床斷面各部分過水斷面面積，m2；χi為河床斷面各部分濕周，m；i=1,2,3分別代表左河灘、河槽、右河灘。

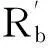
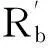
3單參數敏感度分析

3.1本文分析中的一般參數取值

本文采用單參數的敏感度分析，它類似于控制變量法，即保持其他參數不變，僅改變其中1個參數研究計算流量的誤差。

本文分析中一般參數采用：降雨過程為均布雨量過程，雨量集度R=20 mm/h；降雨歷時Tb=1 h；加載步長Dt=1/120 h；漲水歷時t1=5 h；退水歷時t2=10 h，標定洪水最大高程Hs=2 m。

其中，雨量荷載簡化成如圖2所示的20個集中荷載。

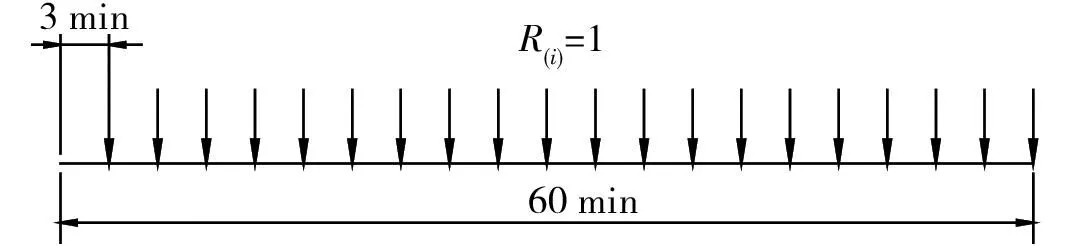
圖2　雨量荷載示意圖Fig.2 Schematic diagram of rain loads

3.2漲水歷時t1誤差對計算流量的影響

對于特定的橋位，漲水歷時t1是個常數，但卻是一個很難準確測量的常數，往往采用目測確定，不可能沒有誤差，顯然這種誤差對計算結果有一定的影響。本文在計算這種影響時，僅改變取t1的大小，使其在范圍內波動，即t1為4.5～5.5 h,其他參數按本文3.1中的一般參數取值。

計算漲水歷時t1的上下波動對計算流量的誤差，圖3為漲水歷時t1的誤差對計算流量Q的影響圖。

圖3　漲水歷時的誤差對計算流量Q的影響圖Fig.3 Influence diagram of swelling duration timeerror on calculation flow rate

3.3退水歷時t2誤差對計算流量的影響

對于特定的橋位，退水歷時同樣是個常數，但卻是一個很難準確測量的常數，往往采用目測確定，不可能沒有誤差，顯然這種誤差對計算結果有一定的影響。在計算這種影響時，僅改變取的大小，使其在范圍內波動，即取為9～11 h,其他參數按“3.1本文分析中的一般參數取值”取值。

計算漲水歷時的上下波動對計算流量的誤差，圖4為漲水歷時的誤差對計算流量Q的影響示意圖。

圖4　退水歷時的誤差對標定流量的影響Fig.4 Influence diagram of recession duration timeerror on calculation flow rate Q

3.4雨量荷載Rb誤差對計算流量的影響

雨量是從鐵路工務段或其他雨量站獲得，受諸多因素的影響，可能存在誤差，這種誤差對計算結果有一定的影響。在計算這種影響時，分為標定雨量和計算雨量來考慮[7]。

標定雨量的上下波動對計算流量的誤差，圖5為標定雨量的誤差對計算流量Q的影響示意圖。

圖5　標定雨量的誤差對計算流量Q的影響圖Fig.5 Influence diagram of calibration rainerror on calculation flow rate Q

計算雨量按式(1)直接計算流量，影響函數為正比例函數形式，圖6為計算雨量的誤差對計算流量的影響示意圖。

圖6　計算雨量的誤差對計算流量Q的影響Fig.6 Influence diagram of calculation rainerror on calculation flow rate Q

3.5標定流量Qb的誤差對計算流量Q的影響

由式(2)可知，在確定流量影響線峰值Cumax時，標定流量Qb在分子上，對計算流量的影響函數為正比例函數，分析可知影響標定流量的主要參數是糙率系數n和河道坡度I,分析可知兩者的影響大小分別為:糙率n在-10%～10%范圍波動時，對洪水流量Qb的誤差值為-9.09%～11.11%，影響程度較大;橋前河道坡度I在-10%～10%范圍波動時，對洪水流量Qb的誤差值為-5.13%～4.88%，影響程度較小。

3.6標定洪水最大高程Hs誤差對計算流量Q影響

標定洪水最大高程Hs由外業測量獲得，受測量儀器精度、洪水時波浪大小的影響，可能存在誤差，這種誤差對計算結果有一定的影響[8]。Hs對標定流量的影響是通過對濕周和斷面面積來作用的，本文分析河道斷面采用的是河底寬10 m，坡度比m=1斷面形式，如圖7所示。

圖7　河道斷面分析圖Fig.7 Analysis diagram of river channel cross section

在計算這種影響時，Hs測量誤差是確定的，不隨Hs變化，但不同的Hs取值對斷面面積、濕周的計算誤差不同，本文取Hs=2 m分析，僅改變Hs取值的大小，使其在范圍內波動，取橋位處最大水深為1.8～2.2 m,其他參數按一般參數采用原則取值。圖8為標定洪水最大高程的誤差對計算流量Q的影響示意圖。

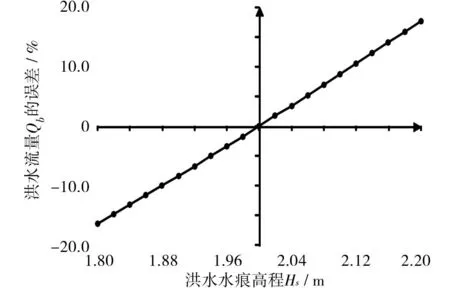
圖8　標定洪水最大高程Hs誤差對計算流量Q的影響Fig.8 Influence diagram of calibration flood maximumelevation error on calculation flow rate Q

若按照滿寧公式計算標定流量，則Qb的影響轉移到標定水位Hs。此參數誤差對計算流量Q的影響與圖8相同[9]。

4基本結論

流量影響線各參數影響計算流量Q的影響程度如表1 所示。

4.1流量影響線是一種可用的方法

為了更加方便地分析每個參數波動對計算流量誤差的影響程度，將流量影響線法的主要參數分析結果匯總，根據每個參數的誤差結果判斷哪些參數是決定流量計算精度的關鍵參數，哪些參數可以相對放松對精度的要求，進而在測量參數過程中節約成本，具體結果見表1。表1表明,當流量影響線參數誤差在“-5%到5%”以內時，流量影響線法的結果可用。

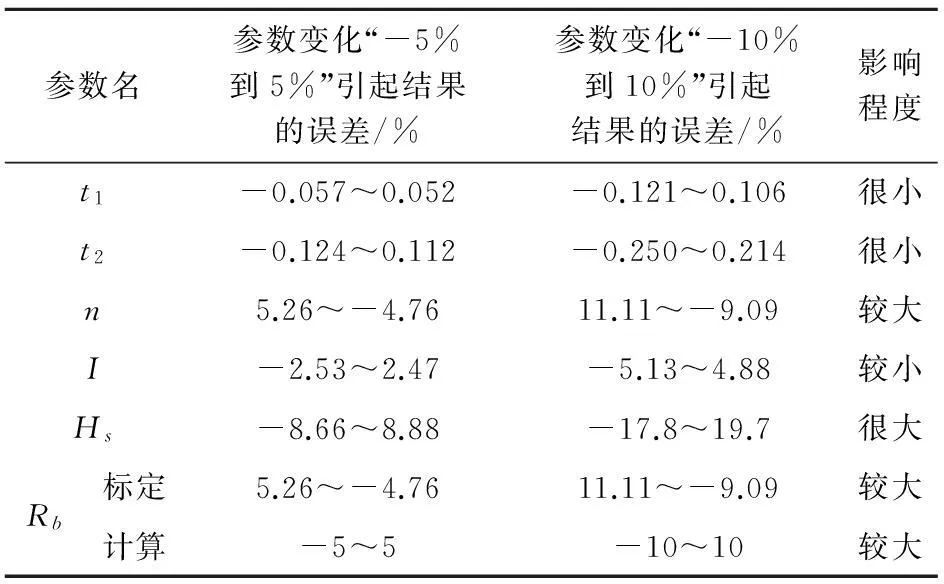
表1　Q的參數敏感度分析匯總

4.2要特別控制標定洪水最大高程的精度

表1表明，洪水最大水位高程Hs對結果的影響最大，其誤差應嚴格控制在5%以內。雨量荷載對計算結果的影響較大,也應控制在5%以內,其他參數對結果的影響不大，可以控制在10%以內。

5結論

1)表1的結論是在“3.1”得出的，進一步研究表明，變化一般參數取值范圍，也可以得出幾乎相同的結果。

2)采用本文研究方法，還可針對雨量荷載系列數量的擴充、河床斷面形式的變化、雨量荷載計算周期的統計周期變化進一步研究參數誤差對計算流量的影響。

參考文獻：

[1] 文雨松.橋涵水文[M].北京:中國鐵道出版社,2005.

WEN Yusong.Hydrology for bridge and culvert[M].Beijing：Railway Publishing House of China，2005.

[2] 鐵道部第三勘測設計院.鐵路工程設計技術手冊:橋渡水文[M].北京:中國鐵道出版社,1999.

The third survey and design institute of railway ministry. Railway engineering design technical manual: Bridge hydrology[M]. Beijing：Railway Publishing House of China，1999.

[3] 李整.文雨松.流量影響線法及其在中小流域橋梁水文中的應用[J]. 鐵道學報,2011,33(6):71-74.

LI Zheng, WEN Yusong. Flow influence line method and its applicationin bridge hydrology of medium and small watersheds[J]. Journal of the China Railway Society, 2011,33(6):71-74.

[4] 崔陽華，雷明鋒.修正的橋梁水害水位單位線預警方法研究[J].鐵道科學與工程學報，2012,9(3)：68-71.

CUI Yanghua, LEI Mingfeng.A modified unit hydrograph method for pre-warning water hazard of bridge [J]. Journal of Railway Science and Engineeringl,2012,9(3)：68-71.

[5] 劉洋宇，李整，文雨松.流量影響線法的可行性驗證分析[J].鐵道建筑，2011(3):23-25.

LIU Yangyu, LI Zheng, WEN Yusong. The feasibility verification analysis of flow influence line method [J]. Railway Construction, 2011(3):23-25.

[6] 張利平，張曉琳，徐霞,等.基于水文模型的雷達監測降雨量誤差傳遞研究[J].水文，2012,32(1):13-16.

ZHANG Liping, ZHANG Xiaolin, XU Xia .et al.The rainfall error transfer research of radar monitoring based on the hydrological model [J].Hydrology, 2012,32(1):13-16.

[7] 胡嫄,李整,文雨松,等.基于流量影響線法的廣東省中小橋換算雨量荷載系列研究[J]. 鐵道科學與工程學報，2011,8(1)：29-33.

HU Yuan,LI Zheng,WEN Yusong,et al. Researches on the conversion rainfall load series ofmiddle& smallbridges based on flow influence line forGuangdong[J]. Journal of Railway Science and Engineeringl, 2011,8(1)：29-33.

[8] 王強，文方針.中小流域橋梁設計流量的H-C-N法[J].鐵道科學與工程學報，2008,5(2)：42-45.

WANG Qiang,WEN Fangzhen.The H-C-N method for calculating bridge design water flowof middle and small river basin[J]. Journal of Railway Science and Engineering, 2008,5(2)：42-45.

[9] 賈借峰，趙井衛，陳客賢.曼寧公式及其誤差分析[J].山西建筑，2010,36(7)：313-314.

JIA Jiefeng, ZHAO Jingwei, CHEN Kexian. Manning’s formula and error analysis[J]. Shanxi Achitecture,2010,36(7)：313-314.

Influence discussion of parameter errors on calculation

flow using flow influence line method

ZHANG Hongcui1，WEN Yusong2

(1. Hubei Road & Bridge Co. Ltd, Wuhan, 430056, China;

2. School of Civil Engineering, Central South University, Changsha, 410075, China)

Abstract:This paper aims to resolve the question of each parameter measurement precision requirement of flow influence line method, with single variable analysis method and using VB programming calculation. The conclusions are made that the measurement error of “calibration flood elevation” , roughness coefficient and rainfall series have large effect on the accuracy of calculation flow, and other parameters have little effect. If the measurement error of the former three parameters is controlled within 5%, and other parameters within 10%, the accuracy of flow influence line method can be ensured. This conclusion can provide reference value for bridge hydrologic survey to improve the calculation precision of flow influence line method and the economic benefit.

Key words:flow influence line method; calculated flow rate; measurement parameters; precision

中圖分類號：U442.3

文獻標志碼：A

文章編號：1672-7029(2015)01-0132-05

通訊作者：文雨松(1950-)，男，湖南桃江人，教授，從事橋梁疲勞和橋梁水害預測研究;E-mail:wenyusong9587@hotmail.com

*收稿日期：2014-06-08