框剪結構基于能量概念的抗側剛度優化研究

?

框剪結構基于能量概念的抗側剛度優化研究

陸鐵堅，楊詩龍，宋寧，王鵬皓

(中南大學 土木工程學院, 湖南 長沙 410075)

摘要:基于勢能駐值原理推導框剪結構的層剛度矩陣，用有限單元法的思想，形成總體剛度矩陣，用于結構的振型分解和周期計算。選取結構滯回耗能需求值與滯回耗能能力值之比與結構所受水平地震作用的乘積作為目標函數，應用振型分解法求解多自由度體系的滯回耗能需求值和能力值，建立框剪結構基于能量概念的抗側剛度優化數學模型。采用罰函數法的思想，將非線性約束優化問題轉化為非線性無約束優化問題，采用MATLAB編制優化程序。最后給出算例，算例表明本文方法和程序是正確可行的。

關鍵詞：框剪結構;抗側剛度;優化；層模型；滯回耗能

框剪結構體系因其獨特的優勢應用廣泛，特別是異形柱框剪結構在中高層住宅體系中發展前景廣闊，且已展開廣泛研究[1-2]。對于框剪結構，從抗震設防的角度來講，多設剪力墻會提高框剪結構的抗側剛度，對抗震是有利的，但剪力墻設置過多，雖有較強的抗側剛度，但剛度增加，周期減小，地震力加大，使得上部材料用量的增加，基礎的設計難度增大，是不經濟的。因此，需尋求剪力墻的最優側移剛度，既使得結構有足夠的抗震能力而又經濟。目前，框剪結構優化問題越來越受到研究人員的重視[3-5]。文獻[3]～[5]有其共同特點：第1，都是根據框剪結構空間協同分析的連續—離散化分析方法，建立基本微分方程，進而得到結構總體剛度方程。因框剪結構空間協同連續微分方程是基于等剛度情況的，文獻[4]和[5]都不能對剪力墻抗側剛度沿樓層變化的情況進行優化，只能處理剪力墻抗側剛度沿樓層不變的優化問題。文獻[3]雖然能夠處理變剛度優化問題，但需提前對剪力墻沿結構高度進行分階，同一階內剛度不變，并且需假設不同階之間抗側剛度的比例關系，所以其優化是受到限制的。本文將運用勢能駐值原理推導框剪結構的層剛度矩陣，從而得到總體剛度矩陣。將用于處理變剛度優化問題，且無需假設不同樓層抗側剛度的比例關系。第2，都以水平地震作用作為單一的目標函數，通過抗側剛度優化使得結構所受地震作用最小，而未考慮結構耗能。近年來，基于能量的抗震設計方法受到人們的廣泛關注[6-8]，從能量的概念去估計地震動能量及評價結構的耗能水準成為未來的趨勢之一。本文的目標函數同時考慮結構所受地震作用和結構的耗能水平，使框剪結構的優化將結構的耗能水準考慮在內。

1框剪結構總體剛度矩陣的建立

借用有限單元法的思想，將整個樓層沿高度劃分單元，采用層單元，每一層為一單元。對于框剪結構，框架部分等效成剪切桿，剪力墻部分等效成彎曲桿，框剪結構在水平荷載作用下的變形為剪彎型，現推導框剪結構剪彎型總體抗側剛度矩陣。

1.1層單元剛度矩陣的推導

層單元兩端自由度和桿端力向量為：

g0gggggg={xi-1,xi,θi-1,θi}T，{F}={Qi-1,Qi,Mi-1,Mi}T

(1)

假設單位虛位移為：

{δd}={δxi-1,δxi,δθi-1,δθi}T

(2)

則彎曲桿彎矩為：

(3)

剪切桿的剪力為：

Fs(x)=Cfi(δxi-δxi-1)/hi

(4)

式中： EIi為第i層抗彎剛度；Cfi為第i層抗推剛度；hi為第i層層高。

則單元的彎矩應變能為：

(5)

剪切應變能為：

(6)

總應變能為：U=U1+U2

(7)

桿端力在虛位移上做的功為： W={δd}T{F}

(8)

可得層間剛度矩陣如下：

(9)

1.2總體剛度矩陣的形成

上面已經推導出了層間剛度矩陣，借用有限元的思想，運用“對號入座”法則形成整個樓層的剛度矩陣，再通過靜力凝聚形成所要的總體抗側剛度矩陣。

2目標函數的選取及計算

本文選取結構滯回耗能需求值與結構滯回耗能能力值之比與結構所受水平地震作用的乘積作為目標函數。理由如下：

滯回耗能需求值與滯回耗能能力值之比能夠反應結構的耗能水準，其值越小，結構耗散地震能量的能力越強；

當設計變量在某一區間時，若耗能水準相差不大，則水平地震作用能為起控制作用。若水平地震作用相差不大，結構的耗能水準能起控制作用。更好的實現結構的優化。

2.1水平地震作用的計算

水平地震作用的計算采用振型分解反應譜法，先需對結構進行振型分解并求解結構各階自振周期，本文第1部分已建立結構總體剛度矩陣，質量矩陣采用對角矩陣時，即可對結構進行振型分解并得到各階自振周期。

第j振型第i質點的水平地震作用標準值為：Fij=αjγjxijGi。各符號的意義見文獻[9]。

2.2滯回耗能需求值和能力值

盛明強[6]給出了單自由度體系的滯回耗能需求譜和能力值計算公式。

需求譜:

(10)

能力值:

(11)

其中：Em為地震動滯回耗能峰值；Tg為特征周期。其余各參數的含義和取值見文獻[6]。

對于多自由度體系，本文采用振型分解法將多自由度體系等效成多個單自由度體系[10][11]，從而得到多自由度體系的滯回耗能需求值和能力值。等效的原則為：總質量相等，各階自振周期與各單自由度體系自振周期對應相等。

3抗側剛度優化數學模型

選取剪力墻彎曲剛度為設計變量，結構滯回耗能需求值與結構滯回耗能能力值之比與結構所受水平地震作用的乘積作為目標函數，以最大層間位移、剛重比、剪重比、框架部分承擔剪力、結構滯回耗能需求值與結構滯回耗能能力值之比為約束條件。即：尋求設計變量使得目標函數取最小值并滿足約束條件。

4程序設計

本文所涉及的優化問題為非線性約束問題，本文采用遺傳優化算法，且本文將約束優化問題轉化為無約束的優化問題，方法為：當不滿足約束條件時將目標函數賦予一個很大的值，例如1015。從而方便的將非線性約束優化問題轉化為非線性無約束優化問題。

本文采用MATLAB編制優化程序，MATLAB中遺傳算法的函數為ga函數，又本文已將非線性約束優化問題轉化為非線性無約束問題，故本文只需編制求解目標函數的子程序。程序計算步驟為：

輸入結構數據與參數；建立結構總體剛度矩陣；振型分解與周期計算；目標函數的計算；約束問題處理。

5算例

對劉敏[3]給出的10層異形柱框架—剪力墻結構住宅進行實例優化設計。該住宅設防烈度為7度，場地類別為2類，層高為3 m，建筑平面見文獻[3]。異形柱框架剪切剛度分別為：Cf1=4.57×108N，Cf2～3=4.89×108N，Cf4～9=4.11×108N，Cf10=3.95×108N，根據建筑初步設計大致計算出的結構等效總重為：G1=4.344 6×106N，G2～G8=2.733 8×106N，G9=3.076 4×106N，G10=1.431 2×106N。

表1　計算結果對比

現對該框剪結構進行優化。按本文方法所編制的程序可以實現任何變剛度的優化，且不需假設不同層之間剪力墻抗彎剛度的比例關系。為了和文獻[3]進行對比，剪力墻按文獻[3]的分階劃分為3階。但不假設不同階之間的比例關系。其程序優化設計結果如下：

1～2層：EwIw=1.23×1011N·m2，3～8層：EwIw=1.18×1011N·m2，9～10層：EwIw=0.786×1011N·m2。和文獻[3]的優化結果進行比較，見表2。

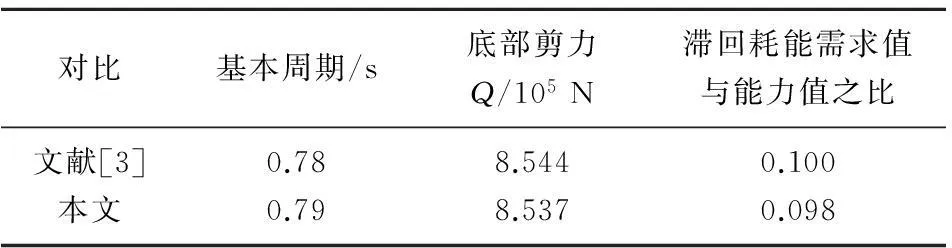
表2　優化結果對比

本文優化結果與文獻[3]優化結果相比，本文優化結果略好，總體上相差不大，但從實用靈活性角度講，文獻[3]假設了各不同層之間剪力墻抗彎剛度的比例關系，如果假設的抗彎剛度比例關系不好，則得不到很好的優化結果，而本文不需假設其比例關系，使得優化更靈活。且本文還將結果滯回耗能需求值與能力值之比作為目標函數的一個因子，即優化時考慮結構的耗能水準。

若將1層至2層劃分為1區段，3層至7層作為一個區段，8層至10層作為一個區段，則本文優化結果為：第1區段抗彎剛度為EwIw=1.248×1011N·m2，第2區段為EwIw=1.053×1011N·m2，第3區段為EwIw=0.72×1011N·m2。其基本周期為0.796 s，底部剪力為8.44×105N，其優化結果更佳。

6結論

1)基于勢能駐值原理推導了層剛度矩陣，其表達式簡潔，用程序很容易形成框剪結構的總體抗側剛度矩陣，算例表明該方法是正確可行的。

2)可以實現任意變剛度的優化問題，使得優化問題更適用更靈活。

3)將結構的耗能水準作為優化目標之一。

4)程序運行時間短，平均耗時2 min能得到優化結果。

參考文獻：

[1] 秦力,賈小剛,楊延波.剪力墻平面布置對異形柱框剪結構地震響應的影響分析 [J]. 建筑結構學報，2010,40(1): 54-56.

QIN Li, JIA Xiaogang, YANG Yanbo. Study on the influence of different layouts of shear-walls on seismic responses of a RC frame-shear wall structure with specially shaped columns [J]. Journal of Building Structures, 2010,40(1): 54-56.

[2] 李偉松.鋼筋混凝土異形柱框架-剪力墻結構基礎隔震性能研究 [D].西安:西安建筑科技大學,2012.

LI Weisong. The base isolation research of reinforced concrete frame-shear wall structure with specially-shaped columns[D]. Xi’an: Xi’an University of Technology, 2012.

[3] 劉敏.中高層異形柱框剪結構抗側剛度優化 [D].武漢:武漢理工大學, 2006.

LIU Ming. Optimal analysis for lateral stiffness in mid-high rise RC frame shear wall structure with special-shaped columns [D]. Wuhan: Wuhan University of Technology, 2006.

[4] 馮宏團.框—剪結構的剪力墻優化研究 [D].西安:西安理工大學, 2005.

FENG Hongtuan. Study on the optimization problem of shear wall in frame-shear structure[D]. Xi’an: Xi’an University of Technology, 2005.

[5] 秦力,宋玉普,張秀文.中高層異形柱框—剪結構的剪力墻抗側剛度優化 [J]. 哈爾濱工業大學學報, 2004,36(8): 1103-1110.

QIN Li, SONG Yupu, ZHANG Xiuwen. Optimal analysis for lateral stiffness of shear wall in mid-highirise RC frame-shear wall structure with special-shaped columns [J]. Journal of Harbin Institute of Technology, 2004,36(8): 1103-1110.

[6] 盛明強.基于滯回耗能的結構抗震性能評價方法研究[D]. 上海:同濟大學,2008.

SHENG Mingqiang. The research on hysteretic energy-based evaluating method of structures’ seismic performance [D]. Shanghai: Tongji University , 2008.

[7] 馬千里.鋼筋混凝土框架基于能量抗震設計方法研究 [D].北京:清華大學, 2009.

MA Qianli. Study on energy-based seismic design methodology and application for RC frame [D]. Beijing: Tsinghua University , 2009.

[8] 瞿岳前.基于能量分析法的地震損失性能控制設計及其智能優化控制設計 [D].西安:西安建筑科技大學, 2003.

QU Yueqian. Seismic damage performance control design and intelligent optimal design based on energy analysis [D]. Xi’an : Xi’an University of Architecture and Technology, 2003.

[9] 郭繼武.建筑抗震設計[M].3版.北京:中國建筑工業出版社,2011.

GUO Jiwu. Seismic design of building[M].3rd Edition. Beijing: China Construction Industry Press, 2011.

[10] 常磊,葉獻國.結構能量反應的振型分解法研究 [J]. 合肥工業大學學報(自然科學版), 2010,33(7):1035-1052.

CHANG Lei, YE Xianguo. Research on modal decomposition method for structure’s energy response equation [J]. Journal of Hefei University of Technology(Natural Science Edition), 2010,33(7):1035-1052.

[11] 常磊,葉獻國.結構能量振型分解反應譜法 [J]. 合肥工業大學學報(自然科學版), 2010,33(8):1202-1207.

CHANG Lei, YE Xianguo. Modal decomposition spectrum method for structure’s energy response[J]. Journal of Hefei University of Technology(Natural Science Edition), 2010,33(8):1202-1207.

Research on lateral stiffness optimization of frame-shear

wall structure based on the concept of energy

LU Tiejian, YANG Shilong, SONG Ning, WANG Penghao

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract:In this paper, based on the principle of resident potential energy, inter-story stiffness matrix for frame-shear wall structure was deduced. The thought of finite element method was used to form the global stiffness matrix, which is helpful to conduct the modal decomposition and calculation of structural natural period of vibration. It is the product of horizontal seismic action, the ration of hysteretic energy demand and hysteretic energy capacity that was selected as the target function. Modal decomposition method was used to calculate the hysteretic energy demand and hysteretic energy capacity of multi-degree freedom system. A mathematical model with respect to lateral stiffness optimization of frame-shear wall structure was founded. In this paper, the nonlinear constrained optimization problem was transformed into nonlinear unconstrained one by adopting the idea of penalty function method. A frame-shear wall structure optimum MATLAB software was developed. Subsequently, combined with a numerical example, the results demonstrate that the method proposed in the paper is accurate and feasible.

Key words:frame-shear wall structure; lateral stiffness; optimization; storey model; hysteretic energy

中圖分類號：TU973.16

文獻標志碼：A

文章編號：1672-7029(2015)01-0150-04

通訊作者：陸鐵堅(1963-)，男，湖南岳陽人，教授，博士，從事高層混合結構抗震研究；E-mail: tiejian@mail.csu.edu.cn

基金項目：國家自然科學基金資助項目(51078354)；湖南省自然科學基金重點資助項目(10JJ2034)

*收稿日期：2014-06-12