改進的螢火蟲群優化算法及其非線性盲源分離

黃浦博，尉 宇，2

(1.武漢科技大學 武漢430070；2.華中科技大學 武漢430047）

1 引言

盲源分離（blind source separation,BSS）的提出起源于“雞尾酒會（cocktail party）”，即從若干觀測到的混合信號中恢復出無法直接觀測的各個獨立原始信號的過程，是信號處理中一個極具挑戰性的課題。“盲”指兩個方面：源信號未知；混合系統未知。源信號的未知因素導致了數學模型很難建立，于是對盲源的分離便順其自然。對盲源分離的實質性研究最早開始于Jutten和Herault[1]兩位學者。之后Sorouchyari和Comon[2]在Signal Processing上發表了關于該研究的文章。在工程實際中應用盲源信號分離時，絕大部分假設信號是線性混疊，但實際上，當信號通過傳感器時很可能會發生非線性畸變，信號常常是非線性的。早期Hyvarinen[3]和Pajunen[4]對非線性混合模型解的唯一性問題進行了討論。國內對盲源分離的研究起步比較晚，但近幾年得到大力的發展。盲源分離方法已形成三大主流，即ICA、NMF[5]和SCA。目前對盲源分離的研究是很有意義的，盲源分離廣泛運用于很多技術中，如語音信號分離與識別、數據通信與陣列信號處理、圖像處理與識別和地學空間信息處理。非線性盲源分離的解決方法可以歸納為以下兩類：運用自組織映射提取信號中的非線性分量的方法；基于假定非線性混合模型的方法。其中包括基于粒子群優化算法、基于自然梯度算法和基于稀疏成分分析算法等。本文采用螢火蟲群優化 （glowworm swarm optimization,GSO）算法來研究非線性盲源分離問題。

2 非線性信號盲分離模型

相比于線性變換模型，非線性變換模型更適用于實際。本文采用Burel[6]兩層感知器結構的非線性模型。

設有m個源信號，有m個觀測信號。源信號s（t）=[s1,s2,s3,…,sm]T和觀測信號x（t）=[x1,x2,x3,…,xm]T之間關系表示如下：

其中,xi表示為：

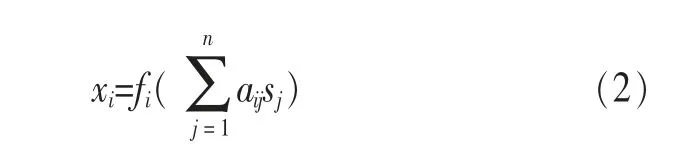
其中，s（t）=[s1,s2,s3,…,sm]T為m個源信號構成的m×1維向量，x（t）=[x1,x2,x3,…,xm]T是m×1維 觀 測 數 據 向 量；m×m維矩陣A稱為信號混合矩陣。F=[f1,f2,f3,…,fm]T是可逆的非線性變換矩陣。該模型為非線性混合[7]與分離模型。

如圖1所示，該系統分為兩部分：混合與分離。混合部分組成：混合信號矩陣A線性混合，獨立非線性失真函數F=[f1,f2,f3,…,fm]T；分離系統組成：gi每一個通道的獨立非線性反變換和W分離矩陣。輸出信號yi（t）表示為：

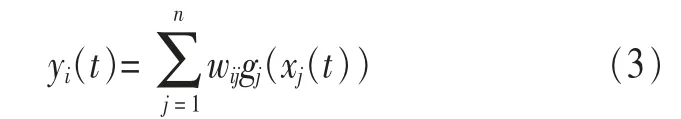
這種數據的表示可寫成矩陣的形式。

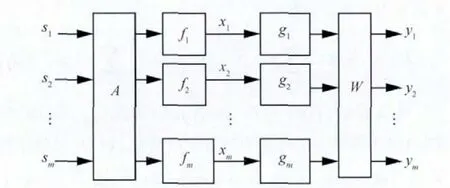
圖1 非線性混合與分離模型

一般而言，非線性混合信號模型是將非線性問題根據某種規則轉化為線性。非線性最大的難度在于參數的估計。這因為空間內存在大量的局部最優化問題。為解決這個問題，先后出現了用RBF（radial basis function，徑向基函數）神經網絡算法、遺傳算法和粒子群優化算法等群智能優化算法，取得了較好的結果。本文擬采用基于優化的螢火蟲群算法解決盲源分離問題。該算法具有操作簡單、宜于并行處理、頑健性強等特點。

3 基于螢火蟲群優化算法的非線性盲分離

3.1 螢火蟲群優化算法簡介

螢火蟲群優化算法是群智能優化算法的一種新思路。已有較多相關的介紹與研究。該算法在解決連續型最優化問題方面表現出了良好的性能。在GSO算法中，每一只螢火蟲分布在二維空間中，空間中螢火蟲本身有螢光，每個螢火蟲都有各自的視覺范圍，即決策域半徑。螢火蟲的位置越好，熒光素值越高，螢火蟲亮度越大，此時的目標函數值越接近所需結果，說明螢火蟲亮度與自己所處位置有關。空間中，較亮的鄰居擁有較高的吸引力吸引附近螢火蟲往自己方向移動，螢火蟲會在決策域半徑內，根據一定的概率選擇方向，并飛向鄰居。不僅如此，決策域半徑范圍的大小會根據鄰居密度的不同而受到影響，從而更新螢火蟲決策域半徑。密度較低，螢火蟲的決策半徑會加大，擴大范圍，便于尋找更多的鄰居；密度較高，則相對地會縮小。GSO算法的目標是為了達到種群尋優。解空間的每一個解被視為自然界中的螢火蟲，初始解隨機分布在搜索空間內，如同螢火蟲隨機出現在規定范圍內。依照螢火蟲的移動方式，解空間內每只螢火蟲按規則移動。移動后更新螢火蟲各參數，通過每次更新，最終使得大量螢火蟲聚集在熒光素較高的螢火蟲周圍，找到多個極值點，達到目標。

群體在優化過程中，每次迭代都由4部分組成：熒光素更新、移動概率更新、位置更新、動態決策域半徑更新。如下是GSO算法的基本步驟描述。

（1）初始階段

初始化時，螢火蟲解個體隨機均勻地散布在解空間內，并且每只螢火蟲擁有相同的熒光素和感知半徑。在搜索空間內隨機生成i（i=1,…,n）只螢火蟲，且所有螢火蟲都帶有熒光素l0，動態決策域r0。

（2）熒光素更新

螢火蟲的熒光素更新規則如下：

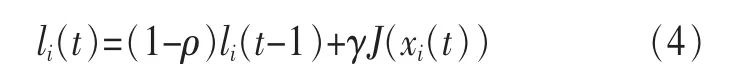
其中，ρ為熒光素衰減因子，介于（0,1），（1-ρ）為亮度衰減率，控制過去經驗比重。γ為比例常數，控制此回合搜索解的經驗比重。J（xi（t））代表的是在t回合第i個螢火蟲所處位置xi（t）對應的適應度函數值，li（t）代表第t回合第i只螢火蟲的熒光素值。螢火蟲的熒光素更新等于螢火蟲的當前適應度值減去隨時間衰減的螢火蟲素值。每一次螢火蟲移動完畢，下一次開始前，螢火蟲熒光素完成更新。

取目標函數值倒數的目的是因為目標函數求極小，目標函數越小的螢火蟲，其亮度就越亮。計算亮度后，螢火蟲與螢火蟲之間在區域決策半徑內以自己的亮度作為溝通的方式，從中挑選一個鄰居，以此移動到較好的群中心位置上。

（3）尋找螢火蟲i的鄰居j

螢火蟲比較自身決策域半徑內鄰居的熒光素的大小選擇飛行方向，尋找熒光素比自己高的鄰居。

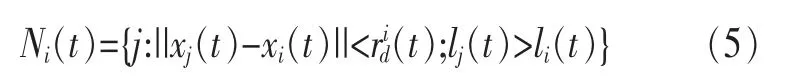
||xj（t）-xi（t）||表示t時刻第i只螢火蟲的鄰居集合。0<（t）≤rs，是螢火蟲j與i的歐幾里得距離。為螢火蟲個體i在t時刻的感知半徑。其中，j∈Ni（t）。

（4）移動概率更新

螢火蟲移動規則如下：

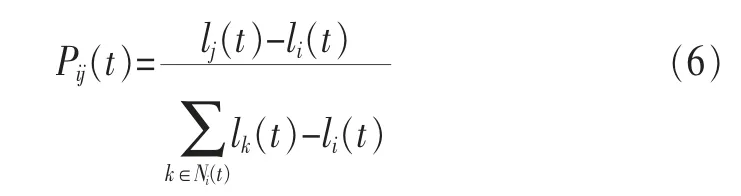
其中，移動方向由鄰居集合中螢火蟲熒光素值決定。Pij（t）表示t時刻第i只螢火蟲向鄰居集合中第j只螢火蟲移動的概率。

（5）位置更新

設移動步長為b（b>0），第i只螢火蟲由移動概率Pij（t）選擇其移動方向移向鄰域內個體j，即輪盤賭法則。第i只螢火蟲的位置更新規則如下：

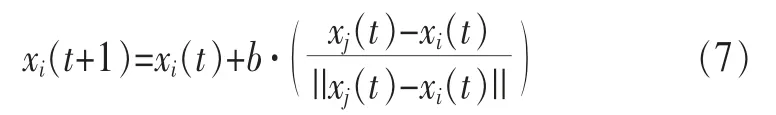
（6）動態決策域半徑更新

螢火蟲群優化算法采用自適應動態領域決策范圍。規則如下：

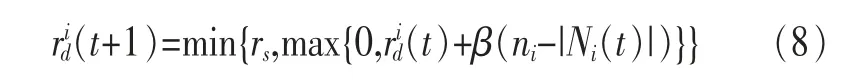
其中，rs為螢火蟲感知范圍，rid（t）表示t時刻第i只螢火蟲的決策范圍，β表示領域變化率，ni表示個體領域集內包含的螢火蟲數目閾值。

（7）判斷是否達到最大迭代次數

若達到，則停止并輸出結果，否則，轉向步驟（2）。

3.2 改進螢火蟲優化算法

GSO算法執行到后期時，會出現很多情況。比如，結果很快會陷入局部最優、求解精度不高、螢火蟲個體在峰值附近出現震蕩現象等。為了改進算法，之前提出了很多方法，如最佳螢火蟲分布算法，在一開始便使得螢火蟲個體的位置最佳，在原算法的基礎上有效改進結果；自適應變步長螢火蟲群優化算法，從搜索過程中改變螢火蟲移動步長，此算法動態調整步長，處理好全局尋優能力和尋優精度之間的關系。

本文也是從算法中期對螢火蟲群進行人工處理。人為將該群體放入鏡子擋板，此時從視覺上看，螢火蟲群體數量大，有效改善了螢火蟲群的布局，豐富了螢火蟲個體的多樣性，豐富的群體多樣性改善了求解精度不高的問題。加入擋板后的螢火蟲群體中，個體由于附近的熒光素強度改變，決策域半徑改變，移動概率更新，相應的位置也會更新，使得螢火蟲群體跳出局部最優，個體重新搜索。本文將該現象稱為“擋板效應”。采用該方式的GSO算法稱為“BGSO”算法。該優化算法的重點在于，當完成一次基本GSO算法后計算得到評價函數值，再加入“擋板效應”，更新評價函數值，并比較兩次評價函數值的大小，保留最優的函數值。下次重復該步聚，直到完成最大迭代次數，并輸出結果。

當遍歷一次后，在群體中加入人工擋板，用表達式表示為：

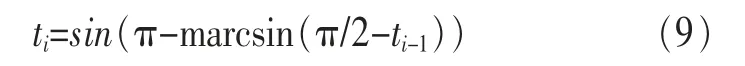
本文中ti∈[-1,1]，取m=4,此時迭代出來的結果互不相關。在原GSO算法中，群體適應度值差別大，在尋優過程中可能還有很少的個體保留下來。加入“擋板效應”的GSO算法，即BGSO算法，豐富了種群多樣性，一定程度上抑制了GSO算法易陷入局部解的發生，提高了求解精度。

3.3 評價函數

對于盲源分離的評價函數可以有很多種形式，比如互信息最小化、信息傳輸最大化和負熵最大化等。本文采用互信息作為評價函數。

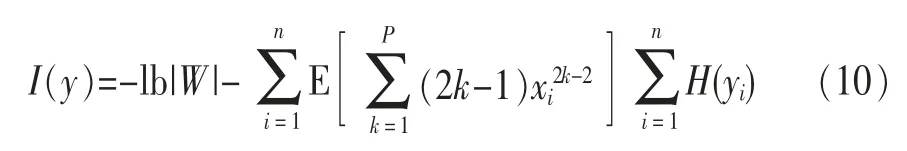
可以看出，I（y）=0時，說明yi相互獨立。式（10）中H（yi）的計算需要估計yi的分布密度函數。對H（yi）的計算常用Edgeworth展開或者Gram-Charlie展開。由于Edgeworth展開在訓練時存在發散問題，這里采用Gram-Charlier展開，其每一分量的熵H（yi）只與它的三階累積量和四階累積量有關：

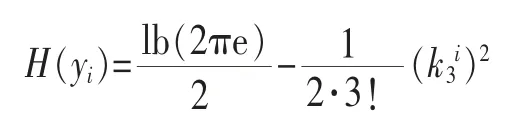
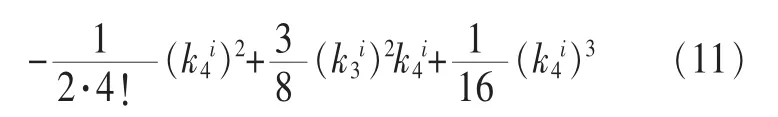
為了使式（11）的期望值為0，方差為1，其在計算前需要對信號進行中心化和白化處理。中心化是減去信號中的均值矢量，從而使其成為零均值變量；然后對觀測矢量進行線性變換得到新矢量，即白化。其各分量不相關且方差為1。這里采用I（y）的倒數作為評價函數，以此增強各隨機變量之間的獨立性。當評價函數得到最大值時，說明各個信號之間最接近獨立。

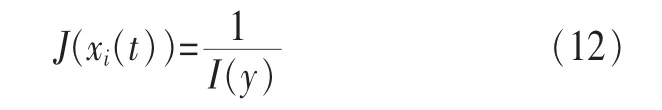
J（xi（t））即式（4）中的適應度函數。式（12）中如果I（y）=0，說明各個信號之間獨立。仿真時，I（y）越小，則越接近所需要結果，此時J（xi（t））也就越大。當J（xi（t））取最大值時，即全局最優解。

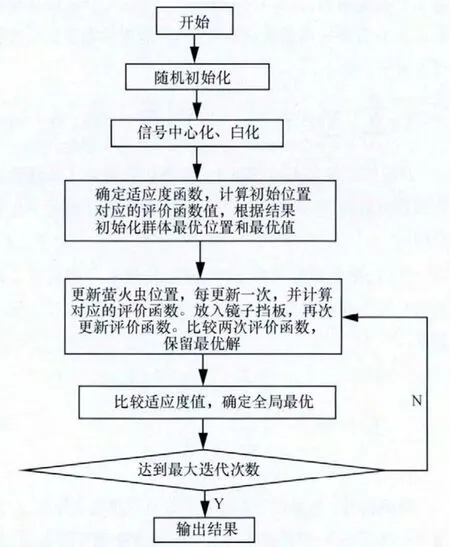
圖2 BGSO算法流程

3.4 算法的應用

非線性混合分離系統中，各個通道的非線性參數空間相互獨立。令非線性參數空間的螢火蟲群為G=[G1，G2，…，Gn]，Gj=[gj1，gj2，…，gjp]。非線性函數與源信號的概率密度函數有關，但由于實際的源信號概率密度未知，因此一般根據不同分布情況采用不同的非線性函數。

基于BGSO算法的非線性盲源分離實現步驟如下。

步驟1讀取源信號。

步驟2初始化非線性去混合函數參數。隨機產生去混合函數參數G=[G1，G2，…，Gn]，Gj=[gj1，gj2，…，gjp]。

步驟3對yi（t）進行中心化和白化處理。按式（10）計算評價函數。

·若某個螢火蟲的評價函數值優于其歷史最優評價函數值，則記當前為歷史最優值，同時該位置為歷史最優位置。

·尋找當前各子群內最優和總群內部最優。

·當子群內歷史最優螢火蟲位置趨近于無變化時，在螢火蟲內部使用“擋板效應”。

所有Sim(Kei，Kej)|?i，j[1，2，…，n]構成一個模糊等價關系，也可表現為一個對稱的相似度矩陣：

步驟4參數更新。對于非線性參數，按照改進螢火蟲優化算法更新螢火蟲熒光素、決策域半徑、位置和適應度函數。

步驟5若達到最大迭代次數，則停止，并輸出結果。否則轉至步驟3。

4 實驗仿真

本次采用兩個語音信號、一個LFM雷達信號和一個高斯白噪聲來驗證算法的有效性。根據所得混合信號，隨機產生混合矩陣A，并求得中心化和白化矩陣O。

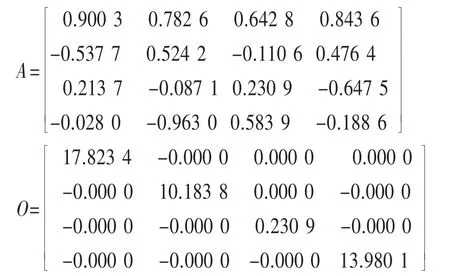
選取的混合函數分別選為：

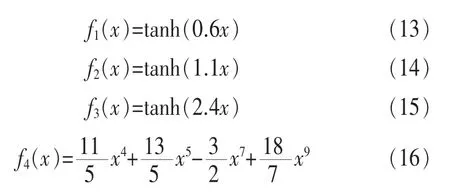
螢火蟲個體數量n=40，最大迭代次數i_max=2 000。結合基本螢火蟲算法，對參數初始化。ρ=0.4,γ=0.6,β=0.08,nt=5,s=0.03,l0=5。隨機產生螢火蟲初始位置xi（0）,初始步長si（0）。連續迭代不變化次數閾值Maxstep=20，并且規定最佳適應度變化率小于1/1 000,認為無變化。源信號圖和中心化以及白化后的混合信號和分離信號如圖3～圖5所示。

求得的性能矩陣P=W·g（f（O·A））=y-1·S如下：

分離矩陣W如下：

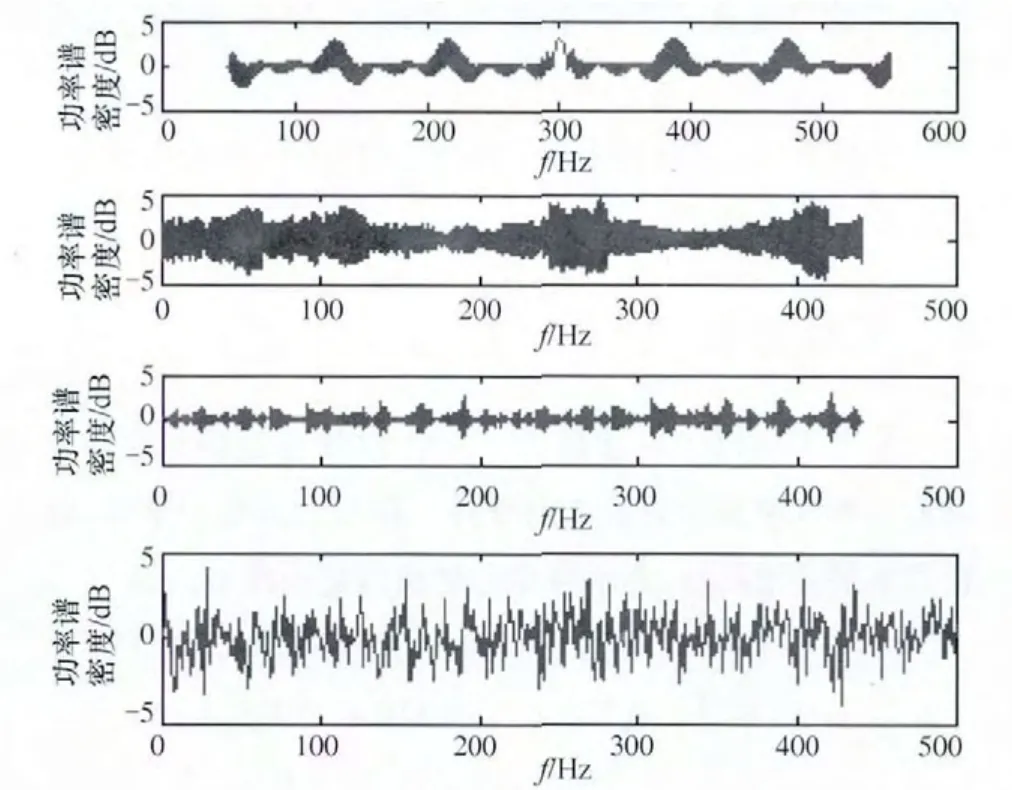
圖3 原信號s（t）

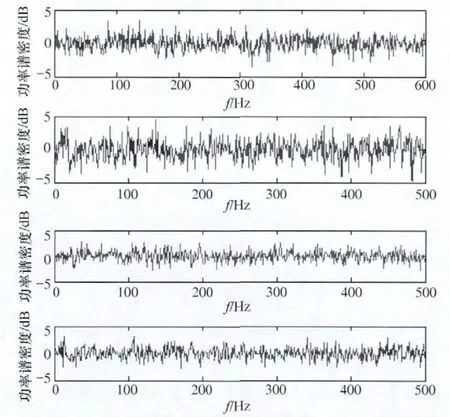
圖4 混合信號x（t)

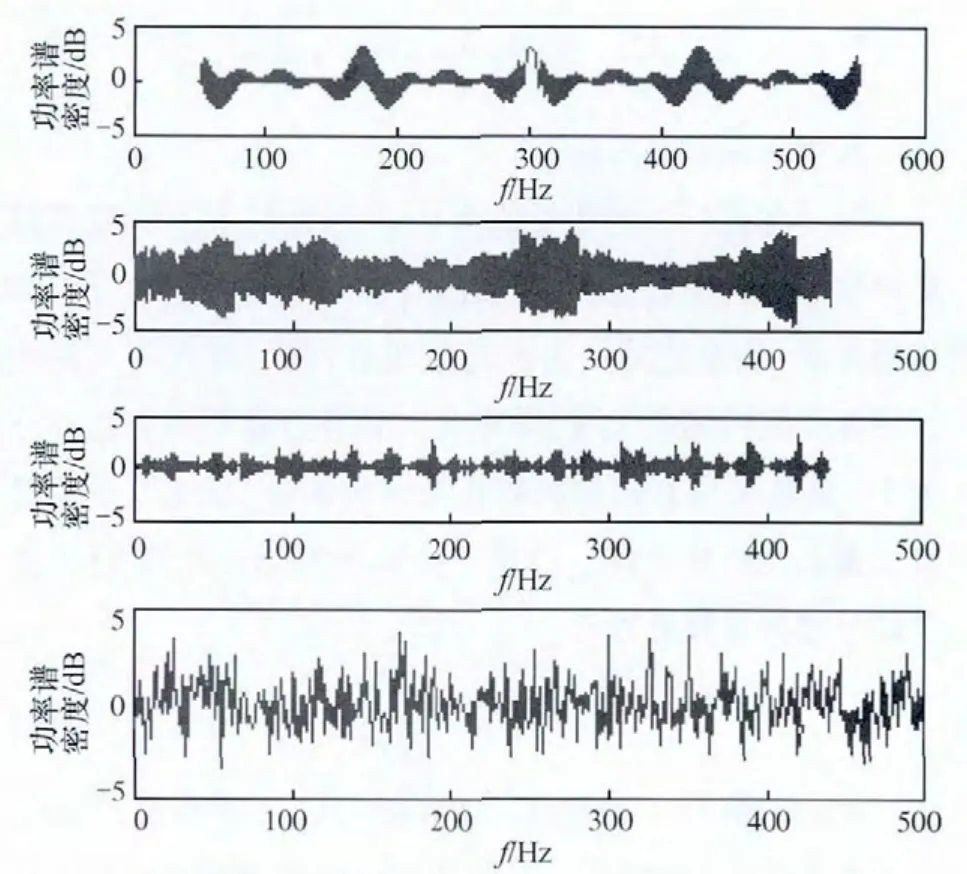
圖5 分離信號y（t）

從性能矩陣中的數值可以看出，每一行都有一個數值遠大于其他數值（例如，第一行第二列遠大于該行其他數值）。而在盲源分離的算法研究中，性能指標常常運用交錯誤差表示。如下：

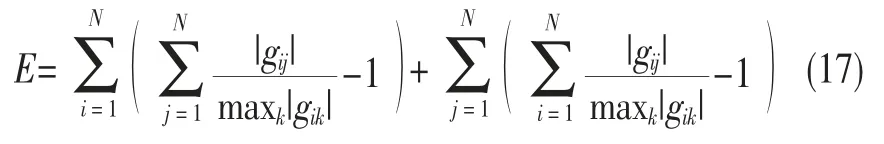
P的性能誤差EP=0.976 1。性能矩陣受到了非線性混合函數的影響，但誤差不大。另一方面證明了信號分離效果較好。

然而，在盲源分離中，分離輸出信號yi與源信號si的相關系數也可以作為一個盲源分離算法的評價標準。定義如下：

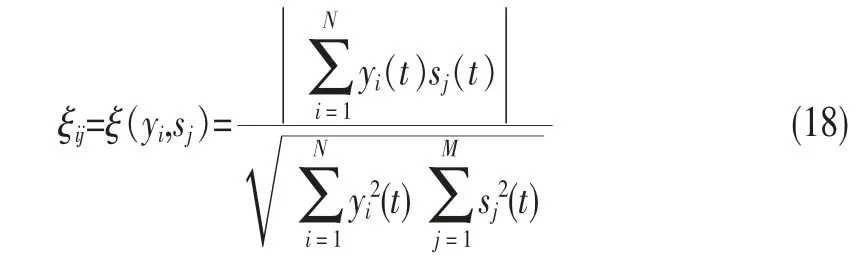
分離信號i與源信號j由于誤差不可能完全分離，ξij的值只能接近于1；而當該值趨近于0或者距離1較遠時，則說明分離并未完成。將分離元素與源信號元素代入式（18）中，可得ξij=0.894 3，該結果接近1。由分析可知，分離結果非常接近源信號，可說明效果理想，分離完成。

在使用BGSO算法的過程中，不同的螢火蟲子群對搜索成功率和達到最優路徑的平均代數有影響。一般采用3～4個子群數的效果較好。子群之間重疊的螢火蟲個數對成功率和達到最優路徑的平均代數也有影響。重疊過多，易導致局部收斂；重疊太少，會導致迭代次數和時間的增加。由此看來對于空間維度較高的情況將使得搜索時間大大增加。

5 結束語

本文采用螢火蟲群算法進行非線性混疊信號盲分離，并在原有的基礎上進行改進，采用鏡面反射的原理，運用到螢火蟲優化算法中，較好地使結果得到改進，精確度得到提高。改進的方式需要讓算法遍歷一次后重新更新，步驟較為復雜。如何將步驟簡化，并將結果與其他算法相比較，將是下一步需要做的工作。

1 Jutten C,Herault J.Blind separation of sources,partⅠ:an adaptive algorithm based on neuromimatic architecture.Signal Processing,1991,24（1）:1～10

2 Comon P.Independent component analysis,a new concept.Signal Processing,1994,36（3）:287～314

3 Hyvarinen A.Independent component analysis for timedependent stochastic processes.Proceedings of the International Conference on Artificial Neural Network（ICANN’98）,Sk’bvde,Sweden,1998

4 Pajunen P,Hyvarinen A,Karhunen J.Nonlinear blind source separation by self-organizing maps.Proceedings of the International Conference on Neural Information Processing,Hong Kong,China,1996（2）:1207～1210

5 Catral M,Han L,Neumann M,et al.On reduced rank non-negative factorization for symmetric non-negative matrices.Linear Algebra Application,2004（393）:107～126

6 Burel G.Blind separation of sources:a nonlinear neural algorithm.Neural Network,1992,5（6）:937～947

7 Woo W L,Khor L C.Blind restoration of nonlinearly mixed signals using multilayer polynomial neural network.IEE Proceedings on Vision,Image and Signal Processing,2004,151（1）:51～61

8 余先川.盲源分離理論與應用.北京：科學出版社，2011 Yu X C.The Theory and Application of Blind Source Seperation.Beijing:Science and Technology Press,2011

9 Krishnanand K N,Ghose D.Theoretical foundations for multiple rendezvous of glowworm-inspired mobile agents with variable local-decision domains.Proceedings of American Control Conference,Minneapolis,MN,USA,2006