單隱含層模糊遞歸小波神經網絡的觀測器設計

聞新　李新　王爾申

(沈陽航空航天大學航空航天工程學部,沈陽 110136)

?

單隱含層模糊遞歸小波神經網絡的觀測器設計

聞新李新王爾申

(沈陽航空航天大學航空航天工程學部,沈陽 110136)

摘要根據模糊神經網絡在非線性函數逼近方面的特性和小波變換具有良好的時頻兩維信號的分析能力,建立了結合兩者優點的單隱含層模糊遞歸小波神經網絡(Single hidden Layer Fuzzy Recurrent Wavelet Neural Network, SLFRWNN),并分析了SLFRWNN的結構、激活函數形式及激活函數對網絡性能的影響.在此基礎上,提出了一種基于SLFRWNN的自適應觀測器設計方法,并通過引入Lyapunov函數,證明了這種觀測器設計方法的穩定性,進而給出該網絡觀測器的初始化和最佳訓練算法;仿真結果表明SLFRWNN觀測器能很好地觀測系統的狀態.

關鍵詞模糊神經網絡;自適應觀測器;非線性系統;仿真

資助項目: 國家自然科學基金(基金號：61571309,61101161)

聯系人： 聞新 E-mail: wen_xin2004@126.com

引言

在復雜的系統工程中,系統存在諸多不確定因素和難以描述的非線性特性,為了解決這些問題,各種各樣的觀測器設計方法不斷涌現,神經網絡在處理非線性問題方面具有較強優勢[1],所以利用神經網絡為基礎的狀態觀測器得到了迅速發展.相比傳統的狀態觀測器,神經網絡狀態觀測器具有較強的自適應性.

狀態估計問題是由測得的輸出量和整個狀態變量不一致引起的[2].狀態觀測器通常是重構一個動態系統的狀態,并在反饋控制、系統監控、故障檢測和故障診斷等方面有著非常重要的應用.非線性系統的觀測器設計已在過去幾十年得到了廣泛的應用[3],如張正強等[4]對具有未建模動態、未知參數、外部干擾的一類多輸入多輸出非線性系統構造了觀測器,Musavi 等[5]利用低成本的微型電子機械系統(Micro-Electro-Mechanical System, MEMS)傳感器設計了自適應模糊神經網絡觀測器應用于GPS系統,為了解決諸如系統模型不確定、多重時間延遲狀態的不確定性和外部干擾等問題，文雄宇等[6]利用自適應小波神經網絡觀測器的跟蹤控制方案對機器人的運行狀態進行了全面的分析.賈鶴鳴等[7]使用神經網絡狀態觀測器設計了一種吊重防搖晃的控制系統.但在設計或構造神經網絡狀態觀測器時,必須遵守一些限定性條件,如要求非線性系統的狀態完全可觀等,因此對于復雜的非線性動態系統的觀測器設計面臨許多復雜的計算問題.因為神經網絡在學習過程中存在收斂速率慢等問題,所以用神經網絡設計非線性系統觀測器的研究還有待進一步完善[8-14].

單隱含層模糊遞歸小波神經網絡(Single hidden Layer Fuzzy Recurrent Wavelet Neural Netnork, SLFRWNN)具有較強的泛化能力,因此它能夠以較高的精度實現函數逼近和系統辨識.本文提出了一種基于SLFRWNN的自適應狀態觀測器設計方法,并應用于非線性系統進行數值仿真驗證.

1單隱含層模糊遞歸小波神經網絡

具有5層神經元的SLFRWNN其模型如圖1所示,其中隱含層使用小波函數作為激活函數.隱含層神經元是一種記憶單元,它存儲了隱含層神經元上一步的輸出,下個時間步時便把記憶的輸出乘以一個反饋增益后再輸入到隱含層.正是這種遞歸記憶的特性,才使該網絡具有動態逼近非線性的性能.

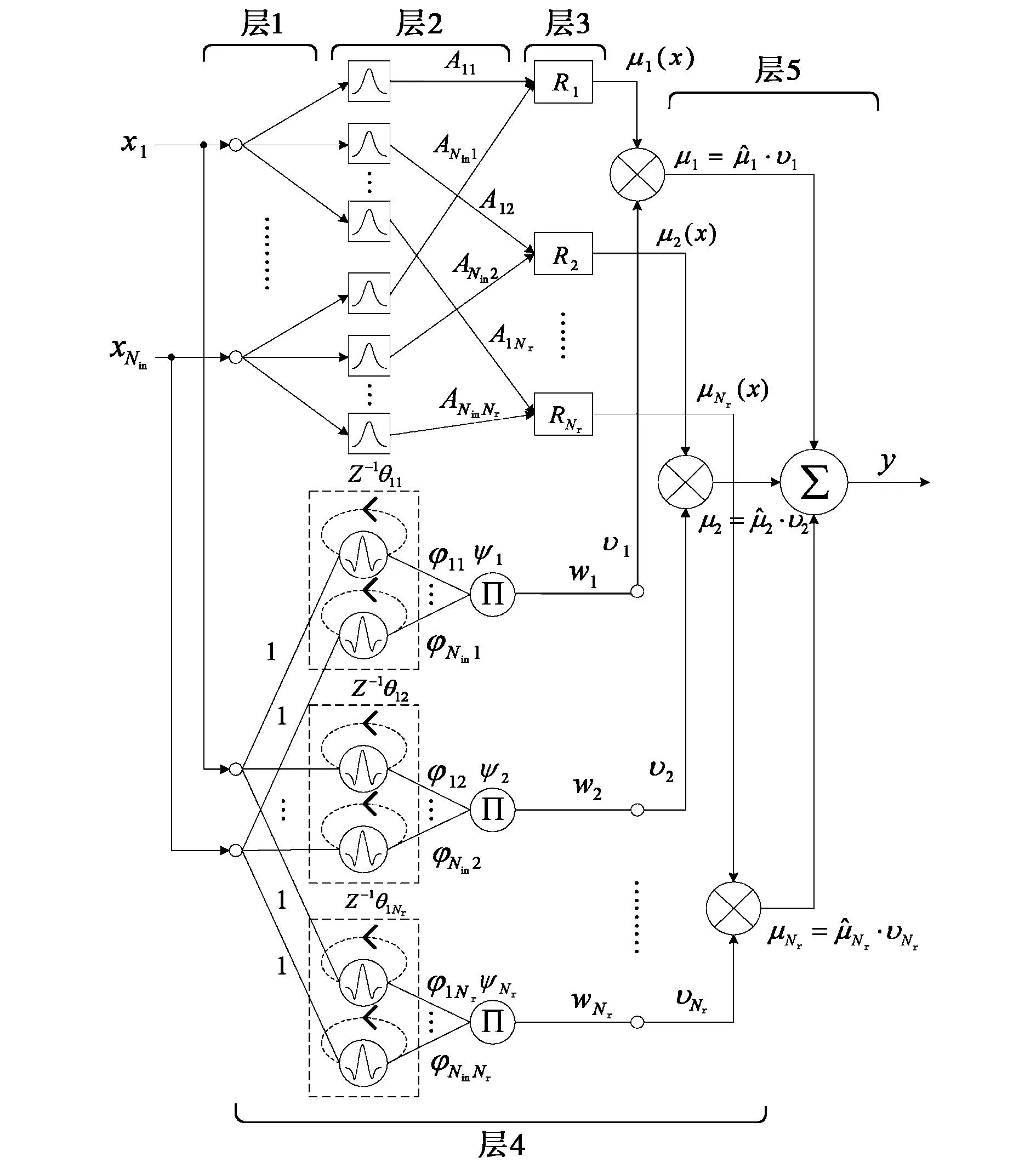
圖1　單隱含層模糊遞歸小波神經網絡模型

圖1中,網絡第二層的輸入隸屬度函數μAIJ(xi)和每個節點的輸出通過式(1)計算:

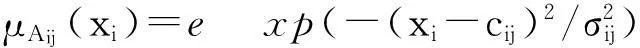
? i=1∶Nin; j=1∶Nr.

(1)

式中: cij表示隸屬度函數中心; σij表示隸屬度函數寬度.

第三層的每個節點表示模糊規則R,其輸出用式(2)表示

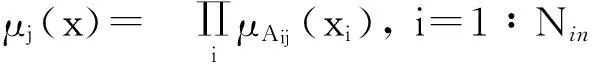
j=1∶Nrand0<μj≤1.

(2)

第四層是網絡的單隱含層,其小波函數作為激活函數見表1所示.

1) 高斯小波函數具有全局映射泛化能力,而且在細化局部方面也有效果,已有多種類型網絡使用該函數作為激活函數,網絡收斂速度不僅快,還能避免過擬合現象.

2) 墨西哥草帽函數是高斯函數的二階導數,它沒有尺度函數及不具正交性,但它具有對稱性和指數衰減性,時頻域具有良好的局部化能力.該函數作為網絡激活函數時,網絡收斂較快,但無法避免陷入局部極小值的缺點.

3)Morlet小波函數是一種復值小波函數,尺度函數不存在且不具有正交性,該函數作為網絡激活函數時,網絡收斂較前兩者慢,但模型過低的自由度會導致欠擬合現象.

表1　小波函數

選擇高斯小波函數作為激活函數,則第四層的每個小波φij為

φijφij(zij(k))=(μij(k)-tij(k))/dij(k),

?i=1∶Nin, j=1∶Nr.

(3)

在離散時間k時,

μij(k)=xi(k)+φij(k-1)·θij(k),

i=1∶Nin, j=1∶Nr.

(4)

式中: tij和dij分別表示小波平移系數和伸縮系數; θij為反饋增益,類似于存儲系數.

則第四層的子小波函數計算為

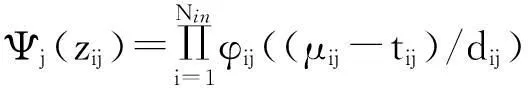
? j=1∶Nr.

(5)

相應的輸出為

υj(k)=wj·Ψj, j=1∶Nr.

(6)

第四層與第三層的節點輸出相乘,結果為

(7)

式中:

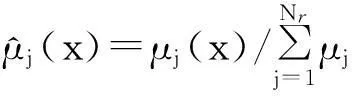
(8)

第五層為網絡的輸出層,其輸出為

(9)

2基于SLFRWNN的自適應觀測器設計

2.1　觀測器設計

考慮如下非線性系統:

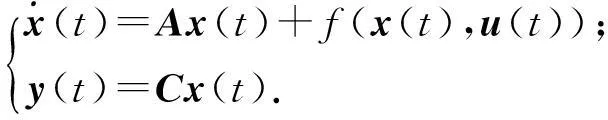
(10)

式中: x(t)∈Rn為狀態變量; u(t)∈Rq為輸入變量;f(x(t),u(t))為非線性函數向量; A∈Rn×n為定常矩陣;在輸出方程中y(t)∈Rm為輸出變量; C∈Rm×m為定常矩陣; (A, C)是可觀測的矩陣對.

針對式(10)的非線性系統,構造圖2所示的SLFRWNN觀測器模型.

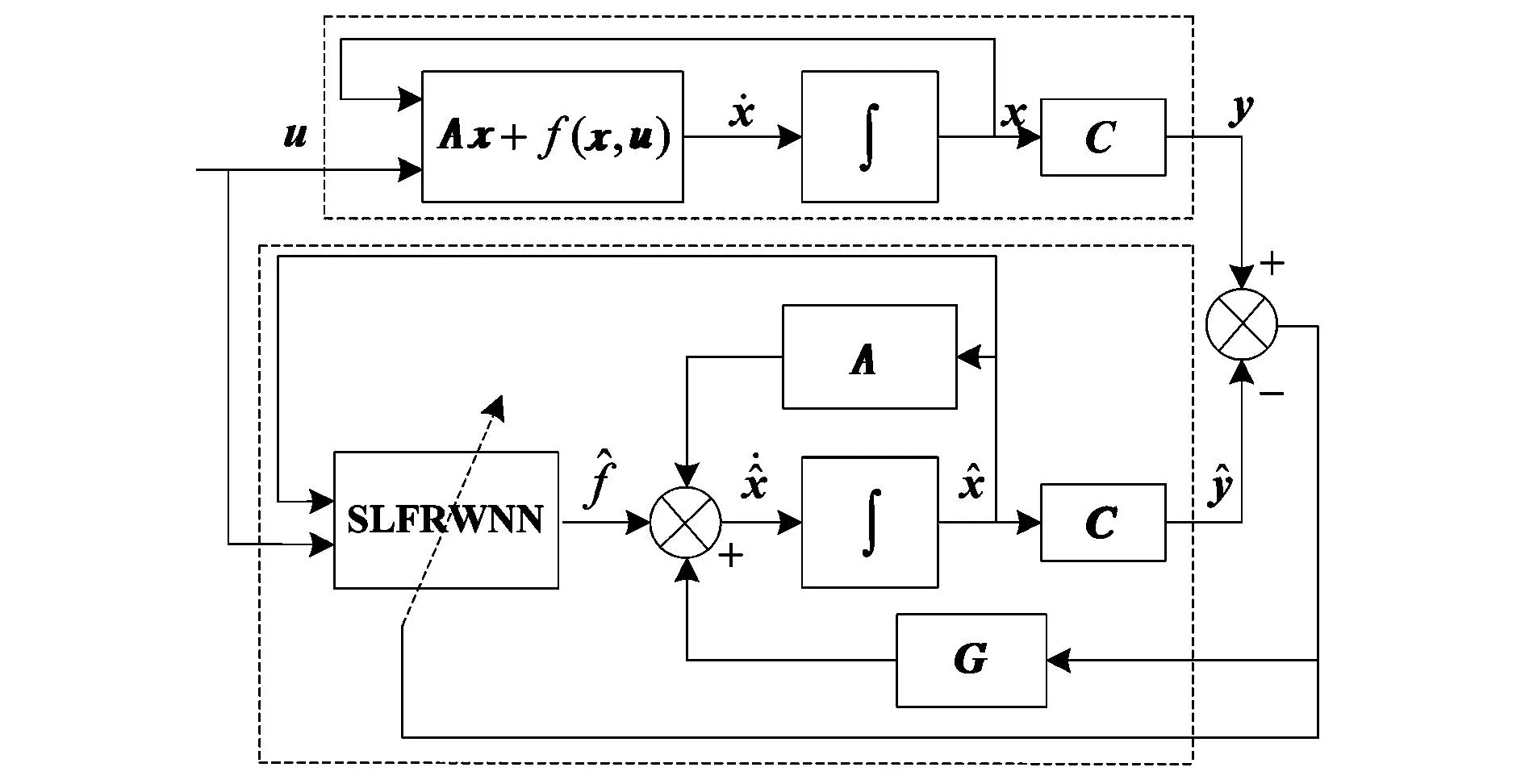
圖2　基于SLFRWNN的狀態觀測器結構圖

式(10)非線性系統的狀態觀測器描述為

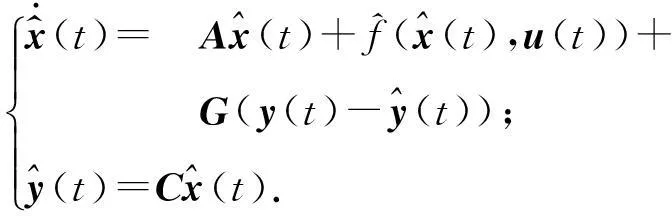
(11)

式中: G為觀測器的增益矩陣,滿足M=A-GC為漸進穩定的Hurwitz矩陣.

假設SLFRWNN的輸入輸出之間的關系為y(t)=WTg(x(t)),給定逼近誤差ε(x(t)),根據神經網絡具有逼近任意非線性系統的性能,則存在εi(x(t))∈ε(x(t))>0使得SLFRWNN能夠逼近非線性函數f(x(t),u(t)),表示如下:

ζ(x(t))=Wg(x(t))+εi(x(t)).

(12)

式中:f(·)是使用高斯小波函數作為激活函數; W為隱含層的權值矩陣,滿足‖εi(x(t))‖≤εN,εN是它的邊界函數,并由隱含層神經元決定.在這里假設權值矩陣W有界,且有‖W‖F≤WM.

根據神經網絡的逼近性能,利用f(x(t),u(t))來替代ζ(x(t)),式(12)變為

f(x(t),u(t))=Wg(x(t),u(t))+

εi(x(t)).

(13)

因此,網絡函數估計為

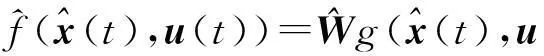
(14)

將式(14)帶入式(11)得

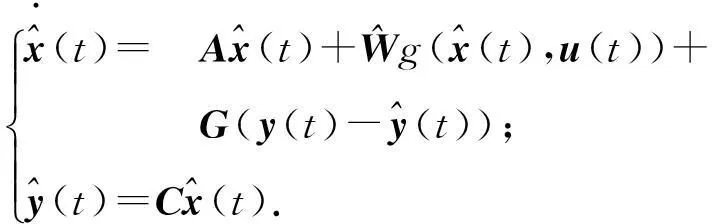
(15)

定義狀態誤差e(t)和輸出誤差ey(t)為

(16)

由式(10)、(15)、(16)可得誤差動態方程為

(17)

2.2　穩定性分析

在一定的條件下定義一個合適的學習規則,能更好地訓練神經網絡,這就需要保障觀測器的穩定性.要使觀測器保持穩定性,一般采用權值校正準則,并引入Lyapunov函數證明權值誤差的有界性.為了更簡潔地證明本文所設觀測器的穩定性,將式(17)進行如下簡化

(18)

式中:

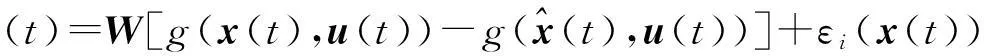
根據文獻[15]對神經網絡權值進行修正，有

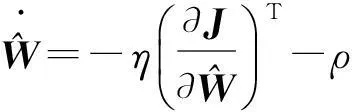
(19)

將式(18)進行求解得

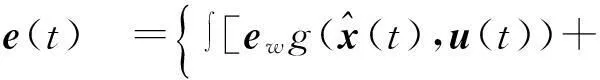
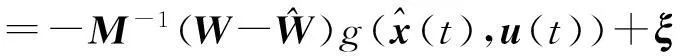
(20)

則

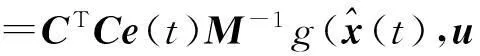
(21)

將式(20)和式(21)代入式(19)得到修正后的神經網絡權值為

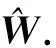
(22)

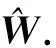
(23)

引入正定的Lyapunov函數[16]為

(24)

式中: P=PT>0為正定矩陣,且對任意正定矩陣Q滿足

MTP+MPT=-Q.

(25)

將式(24)求導可得

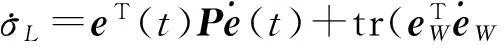
(26)

將式(18)、(23)、(25)代入式(26)得

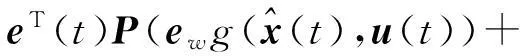
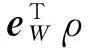
(27)

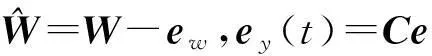
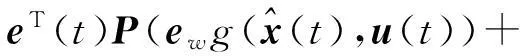
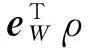
(28)

根據下列不等式組

(29)

可得

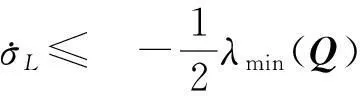
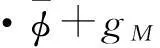
‖δ‖+ρ‖Ce(t)‖·(WM‖eW‖-

‖eW‖2).

(30)

式中:λmin(Q)為矩陣Q的最小特征值;WM=sup(W);gM=sup(g).進一步整理得

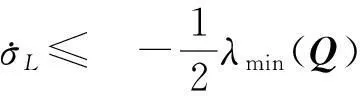
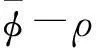
‖eW‖(gM‖δ‖+ρWM‖C‖)].

(31)

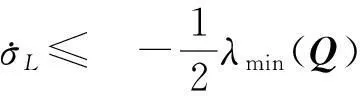
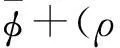
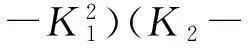
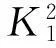
(32)

此外,為了表示權值誤差的界限,式(23)可表示為

ρ‖ey(t)‖W-ρ‖ey(t)‖eW.

(33)

2.3　基于SLFRWNN觀測器的初始化

由于BP神經網絡的收斂速度取決于初始值的選擇,使用GA對SLFRWNN進行初始化.假設有Ns個樣本(x(1),x(2),…，x(k),…，x(Ns)),時間為0到t.SLFRWNN初始化就是基于期望值和網絡輸出值之間誤差的最小化.設yd(k)為期望輸出,yq(k)為實際輸出,因此,在樣本為k時,第q個核函數計算為

(34)

式中

?i=1∶Nin,j=1∶Nr，

(35)

(36)

用向量表示為

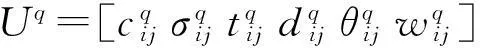
?i=1∶Nin,j=1∶Nr.

(37)

式中:

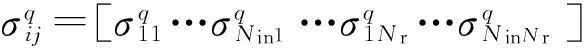
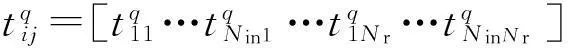
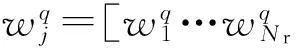
在種群中,用GA在解空間中進行全局搜索,則相應最小適應度函數值的最優解取決于網絡參數的初始值[17].

2.4　基于SLFRWNN觀測器的最佳訓練算法

在神經網絡訓練的過程中,模糊準則后件的所有參數需要進行自動調整,本文使用反向傳播算法對后件參數進行調整.令yd(k)和y(k)分別為網絡在離散時間k時的期望輸出和實際輸出,則k時刻的網絡誤差為

e(k)=yd(k)-y(k).

(38)

取代價函數

(39)

設網絡從時間步1工作到時間步Nr,則每個周期的總誤差函數為

(40)

后件參數wj、tij、dij和θij使用式(41)～(44)進行調整:

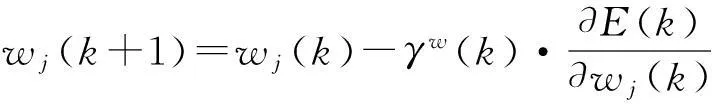
(41)

(42)

(43)

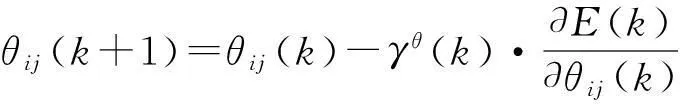
(44)

式中:γ=[γw,γt,γd,γθ]表示學習速率,即0<γ<1.式(41)～(44)的偏導數值為

=(y(k)-yd(k))·

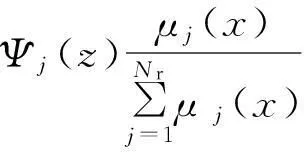
(45)

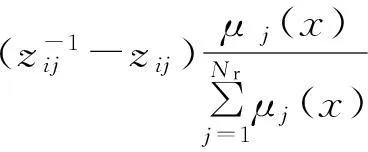
(46)

(47)

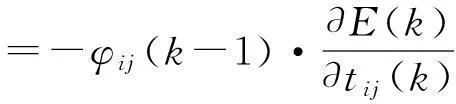
(48)

式(36)和式(45)～(48)均使用高斯小波函數作為小波母函數.

3系統仿真

考慮如下非線性系統,狀態方程如式(10),其對應參數值如下：

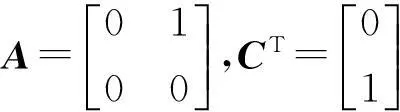
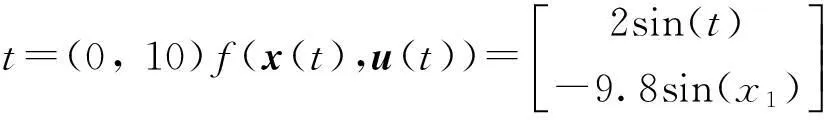
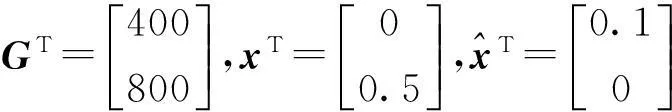
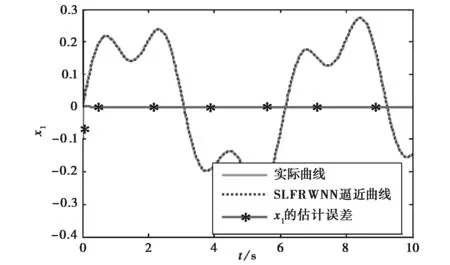
圖3　x1的狀態估計曲線以及估計誤差

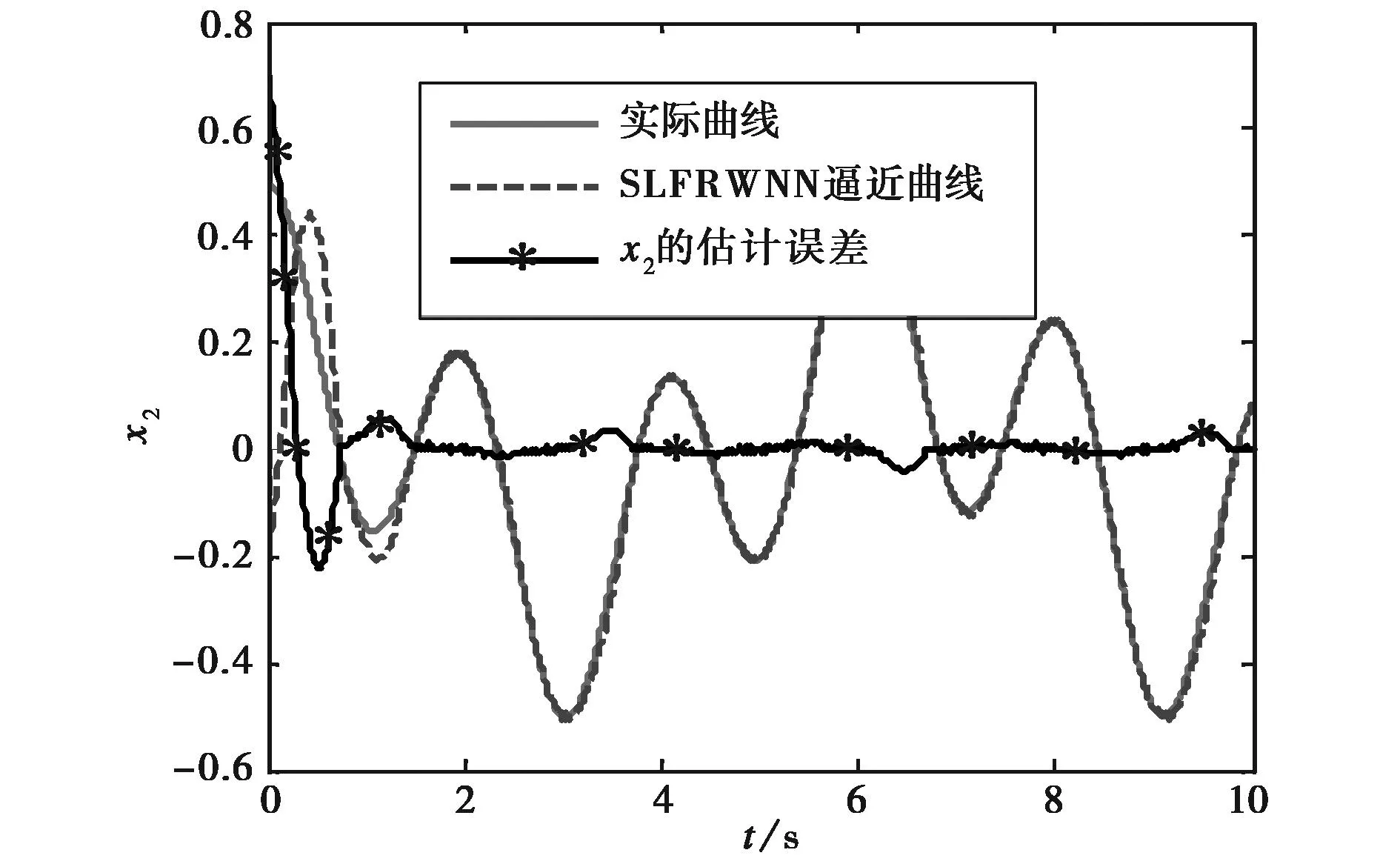
圖4　x2的狀態估計曲線以及估計誤差

由圖3和圖4的仿真曲線可以看出,SLFRWNN自適應觀測器對非線性系統的狀態變量具有很好的跟蹤能力.圖4在開始階段的逼近效果不是很好,這主要是由于狀態變量進行初始化時,初始值的選取是按照經驗進行選取,從而造成開始階段的估計誤差相對較大.圖4中狀態誤差有微小的波動,主要是由狀態變量存在輕微的震蕩引起的,震蕩周期大約為1ms.從圖5可以看出,在剛開始階段,SLFRWNN的跟蹤估計誤差相對較大,但隨著時間的推移,誤差值越來越小,其SLFRWNN平均估計誤差為0.041,這歸結為高斯函數作用的結果.圖3和圖4的仿真結果最終表明,該自適應觀測器可以克服微小的波動,從而實現系統狀態的快速跟蹤.

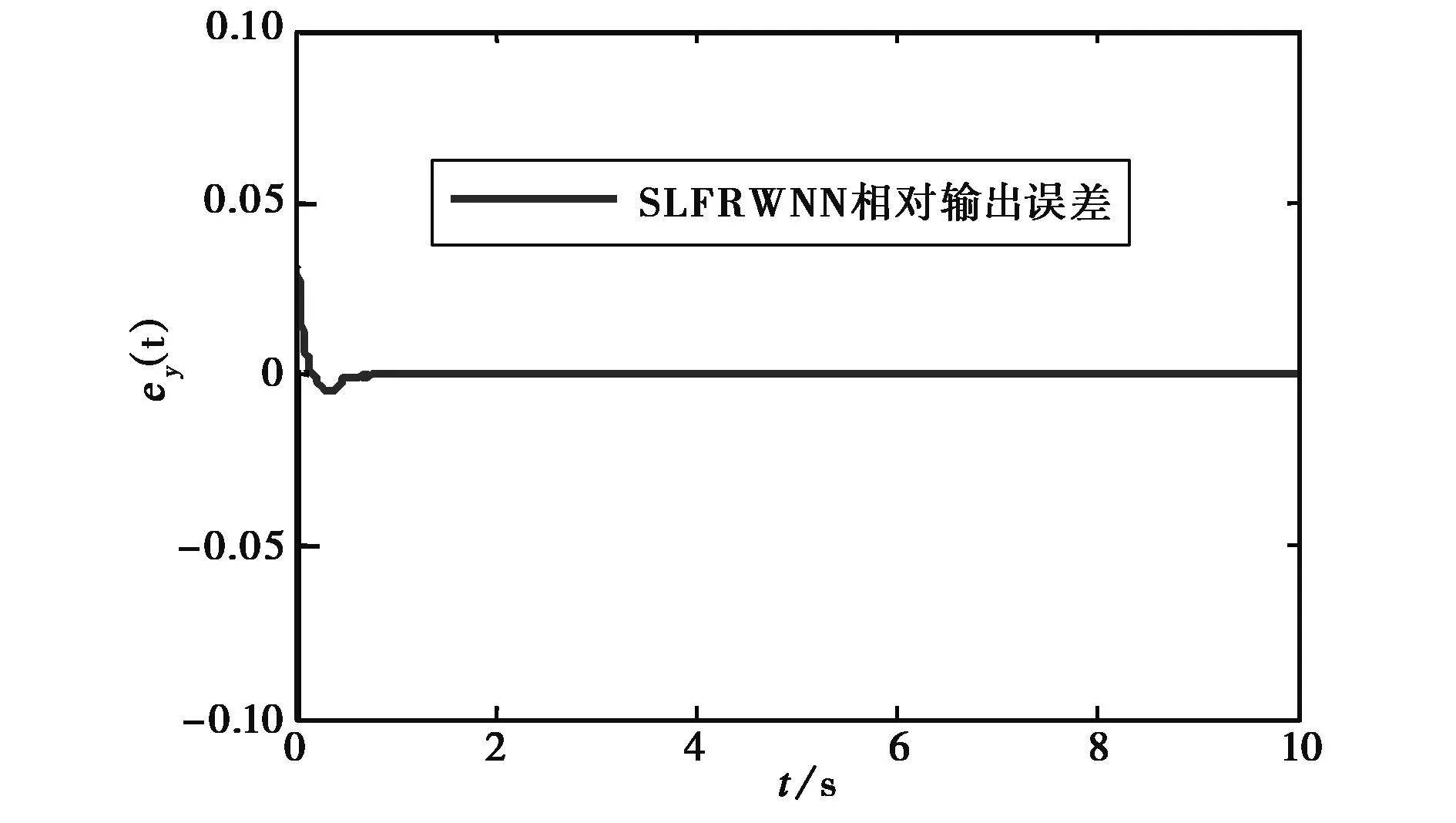
圖5　輸出y的相對誤差

4結論

本文建立了5層單隱含層模糊遞歸小波神經網絡,該網絡后件具有較少的神經元,并能有效地跟蹤快速變化的過程,并在此基礎上使用該神經網絡設計了一種新的自適應觀測器.仿真結果表明,該自適應觀測器能夠快速有效的跟蹤狀態參數的變化,并對非線性動態神經系統具有很好的自適應逼近能力.但是,由于神經網絡自身的缺陷,如網絡訓練時間長、迭代次數多、優化的參數多等,這些問題有待于進一步的完善.

參考文獻

[1]李江曼, 趙振維, 郭立新, 等. 地基微波輻射計分段正交神經網絡方法遙感陰天大氣[J]. 電波科學學報, 2014, 29(6): 1105-1109.

LIJiangman,ZHAOZhenwei,GUOLixin,etal.Asubsectionorthogonalneuralnetworktechniquefortheground-basedradiometertoremotelysensecloudyatmosphere[J].ChineseJournalofRadioScience, 2014, 29(6): 1105-1109. (inChinese)

[2]BESANCONG.Nonlinearobserversandapplications,in:lecturenotesincontrolandinformationsciences[M].Berlin:Springer-Verlag, 2007.

[3]EKRAMIANM,SHEIKHOLESLAMF,HOSSEINNIAS,etal.AdaptivestateobserverforLipschitznonlinearsystems[J].Systems&ControlLetters, 2013,62(4):319-323.

[4]ZHANGZhengqiang,XUShengyuan.Observerdesignforuncertainnonlinearsystemswithunmodeleddynamics[J].Automatica, 2014, 50(1): 80-84.

[5]MUSAVIN,KEIGHOBADIJ.Adaptivefuzzyneuro-observerappliedtolowcostINS/GPS[J].AppliedSoftComputing, 2015, 29(1): 82-94.

[6]YUWS,WENGCC.Anobserver-basedadaptiveneuralnetworktrackingcontrolofroboticsystems[J].AppliedSoftComputing, 2013, 13(12): 4645-4658.

[7] 賈鶴鳴, 張利軍, 齊雪. 基于神經網絡的水下機器人三維航跡跟蹤控制[J]. 控制理論與應用, 2012, 29(7): 877-883.

JIAHeming,ZHANGLijun,QIXue.Three-dimensionalpathtrackingcontrolforautonomousunderwatervehiclebasedonneuralnetwork[J].ControlTheoryandApplications, 2012, 29(7): 877-883. (inChinese)

[8] 嵇艷鞠, 徐江, 吳瓊, 等. 基于神經網絡電性源半航空視電阻率反演研究[J]. 電波科學學報, 2014, 29(5): 973-980.

JIYanju,XUJiang,WUQiong,etal.Apparentresistivityinversionofelectricalsourcesemi-airborneelectromagneticdatabasedonneuralnetwork[J].ChineseJournalofradioScience, 2104, 29(5): 973-980. (inChinese)

[9]YANGDongsheng,LIUXinrui,XUYukun,etal.Stateestimationofrecurrentneuralnetworkswithintervaltime-varyingdelay:animproveddelay-dependentapproach[J].NeuralComputAppl, 2013, 23(3): 1149-1158.

[10]SCHWENKERF,KESTLERHG.Threelearningphasesforradialbasisfunctionnetworks[J].NeuralNetworks, 2001, 14(2): 439-458.

[11]CHENGCaixia,SUNFuchun,ZHOUXinquan.Onefiredetectionmethodusingneuralnetworks[J].TsinghuaScienceandTechnology, 2011, 16(1): 31-35

[12]ADHYARUDM.Stateobserverdesignfornonlinearsystemsusingneuralnetwork[J].AppliedSoftComputing, 2012, 12(8): 2530-2537.

[13]曹海青, 王渝, 杜明芳, 等. 小型漂浮式衛星天線自抗擾控制器的研究[J]. 電波科學學報, 2014, 29(5): 841-847.

CAOHaiqing,WANGYu,DUMingfang,etal.Activedisturbancerejectioncontrollerforsmall-sizedfloatantenna[J].ChineseJournalofRadioScience, 2014, 29(5): 841-847. (inChinese)

[14]GRIPHF,SABERIA,JOHANSENTA.Observersforinterconnectednonlinearandlinearsystems[J].Automatica, 2012, 48(7): 1339-1346.

[15]SHAIKFA,PURWARS,PRATAPB.Real-timeimplementationofChebyshevneuralnetworkobserverfortwinrotorcontrolsystem[J].ExpertSystemswithApplications, 2011, 38(10): 13043-13049.

[16]ABDOLLAHIF,TALEBIHA.Astableneuralnetworkobserver-basedobserverwithapplicationtoflexiblejointmanipulators[J].IEEETransactiononNeuralNetwork, 2006, 17(1):118-129.

[17]TOFIGHIM,ALIZADEHM,GANJEFARS,etal.Directadaptivepowersystemstabilizerdesignusingfuzzywaveletneuralnetworkwithself-recurrentconsequentpart[J].AppliedSoftComputing, 2015, 28(3):514-526.

聞新(1961-),男,遼寧人,沈陽航空航天大學博士生導師,南京航空航天大學航天控制系主任,主要研究的方向為航天器總體設計與故障診斷．

李新 (1988-),男,江蘇人,沈陽航空航天大學航空航天工程學部碩士研究生,主要研究方向為智能檢測與診斷及航天器故障診斷技術．

王爾申(1980-),男,遼寧人,博士,副教授,在站博士后,主要研究方向為衛星導航、智能信號處理．

張忠祥, 孔勐, 陳明生, 等. 一種計算復雜天線散射截面的新型快速方法[J]. 電波科學學報,2015,30(6):1205-1210. doi: 10.13443/j.cjors. 2014103003

ZHANG Zhongxiang, KONG Meng, CHEN Mingsheng, et al. A novel method of RCS fast calculation with complex antenna structure[J]. Chinese Journal of Radio Science,2015,30(6):1205-1210. (in Chinese). doi: 10.13443/j.cjors. 2014103003

Observer design for the single hidden layer fuzzy

recurrent wavelet neural network

WEN XinLI XinWANG Ershen

(FacultyofAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136,China)

AbstractThe fuzzy neural network has good nonlinear function approximation properties, and wavelet transform has good time-frequency signal analysis capabilities. The single hidden layer fuzzy recurrent wavelet neural network (SLFRWNN) is developed by combining with the advantages of both in this paper. The structure of networks, the form of its activation functions and its influence on SLFRWNN are analyzed. Then a design method of adaptive observer based on the single hidden layer recurrent fuzzy wavelet neural network is proposed. The Lyapunov function is introduced to prove the stability of this observer design method. And the network observer of initialization and the optimal learning algorithm is given. The final simulation results show that the single hidden layer neural fuzzy recurrent wavelet network observer can easily observe the state of the system.

Key wordsfuzzy neural networks; adaptive observer; nonlinear systems; simulation

作者簡介

收稿日期：2014-10-14

中圖分類號TP183

文獻標志碼A

文章編號1005-0388(2015)06-1197-08