基于支持向量機集成的圓極化微帶天線設計

田雨波　孫菲艷　任作琳

(江蘇科技大學電子信息學院,鎮江 212003)

?

基于支持向量機集成的圓極化微帶天線設計

田雨波孫菲艷任作琳

(江蘇科技大學電子信息學院,鎮江 212003)

摘要人工神經網絡(Artificial Neural Network,ANN)設計圓極化微帶天線(Circularly-polarized Microstrip Antenna, CPMSA)時需要進行大量數據樣本的準備,網絡結構一般都比較復雜.為了解決這個問題,利用支持向量機(Support Vector Machine, SVM)

在解決小樣本數據處理問題時具有擬合精度高、泛化能力強、結構簡單等優點,結合二進制粒子群(Binary Particle Swarm Optimization, BiPSO)算法選擇出合適的SVM個體參與集成,形成一種基于BiPSO算法的選擇性SVM集成(SVM Ensemble, SVME)方法,并將該方法用于單饋切角方形CPMSA的綜合設計. 仿真結果表明:這種SVME方法提高了算法的魯棒性和有效性,有更好的預測精度,通過與ANN、SVM以及現有文獻的預測結果對比可以看出,由該模型得出的結果優于此問題的已有結論.

關鍵詞圓極化;微帶天線;切角;粒子群優化;支持向量機集成

資助項目: 國家自然科學基金(61401179)

聯系人： 孫菲艷 E-mail：826029488@qq.com

引言

微帶天線(Microstrip Antennas, MSA)是在背面有導體接地板的介質基片上粘貼一塊導體薄片而形成的天線,主要優點有體積小、剖面薄、價格低廉、重量輕等[1-2]. 眾所周知,與線極化微帶天線相比,圓極化微帶天線(Circularly-polarized Microstrip Antennas, CPMSA)最主要的優點就是接收輻射來波時不用調整極化角,且其輻射的電磁波可以被任意極化方向的天線接收到,近年來已被廣泛地應用于全球定位系統、無線電頻率識別系統、移動衛星通信以及無線局域網等領域[3]. 通常,CPMSA有單路饋電和雙路饋電結構,雙路饋電結構的CPMSA的主要特點是有一個寬廣的軸比帶寬,但卻是以增加結構的復雜度和天線的尺寸為代價的;單路饋電結構的CPMSA只需要在適當的位置稍微變動天線的結構去刺激產生相位相差90°的正交模型,因此,單路饋電結構的CPMSA具有結構簡單,容易制造和成本低廉等優勢;目前,制造單路饋電結構的方形CPMSA發射器的常用方法是均勻地裁剪一對較小的切角[4].

20世紀80年代初,M. Haneishi和S. Yoshida開創性地提出了單路饋電結構的切角CPMSA的設計原理[5],原理指出,方形微帶天線中品質因數Q的實際值必須事先通過經驗公式、電磁仿真或者實際測量獲得. 眾所周知,電磁仿真需要巨大的計算工作,而實際測量又是非常昂貴的,因此,經驗公式是計算出Q的實際值的一種相對較好的方法. 經過驗證得知,在常見的工程應用中,由D. R. Jackson等人提出的公式是可行準確的[6]. 然而,經驗公式需要復雜的數學計算和強大的知識背景,本文提出了一種基于二進制粒子群優化(Binary Particle Swarm Optimization, BiPSO)算法的支持向量機集成(Support Vector Machine Ensemble, SVME)方法,并將其用于單路饋電CPMSA的綜合建模. SVM具有小樣本學習、泛化能力強、結構簡單等優點[7],與神經網絡集成類似[8],SVME是通過對有限個SVM獨立進行訓練,并將其預測結果進行集成,集成可以顯著地提高SVM準確表達復雜對象的能力[9]. 本文主要通過BiPSO 算法合理選擇組成SVME的各個SVM,使個體間保持較大的差異度,減小多維共線性和樣本噪聲的影響. 通過和人工神經網絡(Artificial Neural Network,ANN)、單個SVM的預測結果對比,基于BiPSO算法的SVME有更好的預測精度,提高了算法的魯棒性和有效性.

1圓極化微帶天線模型

文獻[10]討論了一種如圖1所示的單饋切角方形CPMSA,尺寸為L×L,介質基片厚度為H,損耗角為tanδ,相對介電常數為εr,對稱切角尺寸為Lt. 基于文獻[5]給出的結論,產生圓極化條件如下:

(1)

(2)

式中: Qt是方形微帶天線品質因數; f0是在最好的軸比條件下的頻率; fr是方形微帶天線的諧振頻率. 這一條件意味著當設計單饋切角方形CPMSA時,應該首先獲得諧振頻率和方形微帶天線的品質因數.

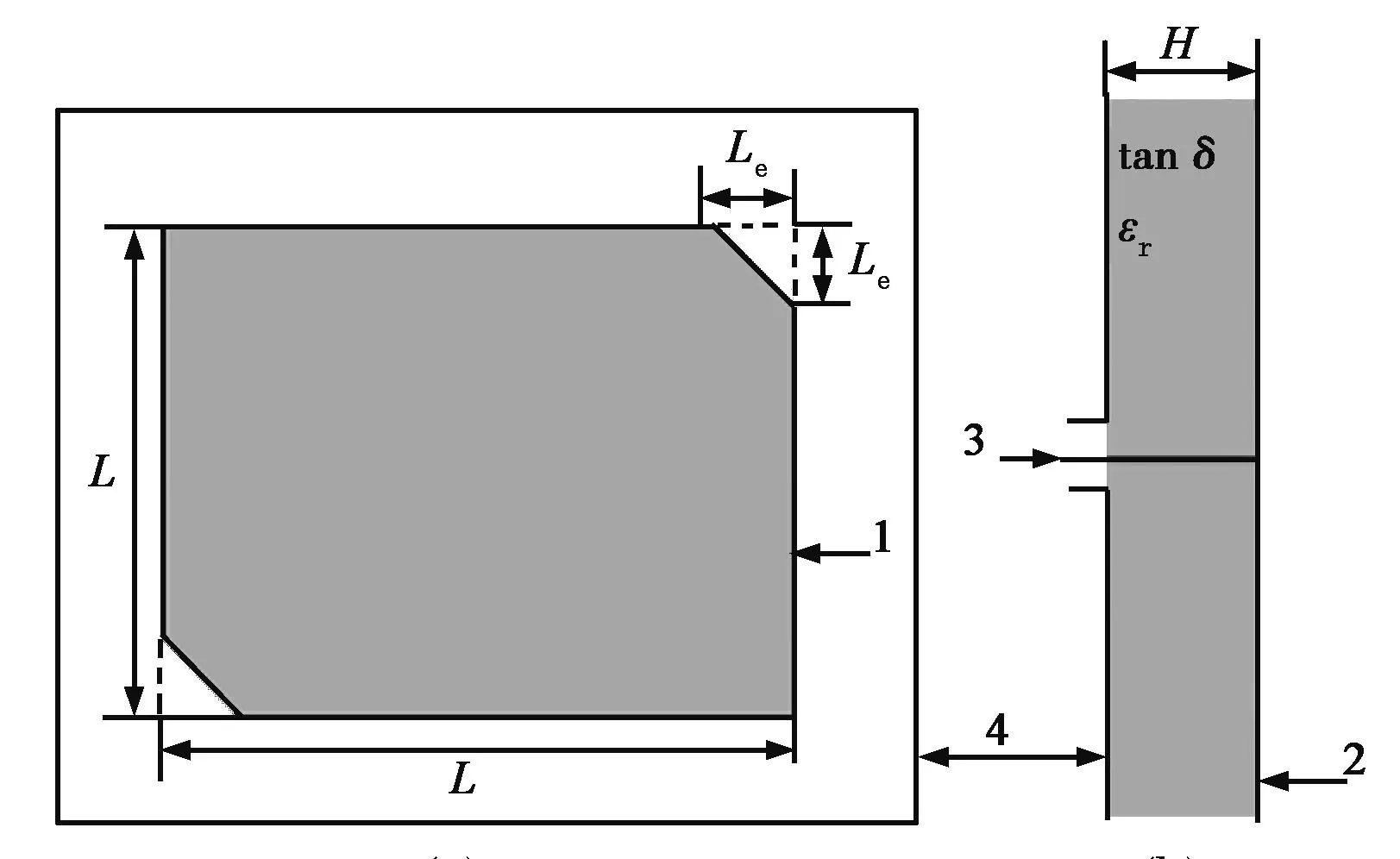
(a)俯視圖　　　　 (b)側視圖1切角貼片 2介質襯底 3探針饋電 4接地基板圖1　微帶天線結構圖

實驗表明,基于傳輸線的經驗公式在H≤0.1λg情況下對于常見的工程應用是準確的[6,11]. 當一個方形微帶天線工作在TM10模式下,基于傳輸線公式計算諧振頻率公式為[11]

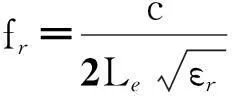
(3)

式中: c是電磁波在自由空間的速度; Le是方形貼片的實際長度. 公式(3)在文獻中常常使用有效介電常數εe代替相對介電常數εr,然而,由D.R.Jackson等人完成的實驗[11]已經證明使用εr與Hammerstad給定的邊緣長度[12]可以得到更加準確的結果.

方形微帶天線的品質因數Qt與介質損耗Qd、導體損耗Qc、空間輻射損耗Qsp和表面波損耗Qsw等有關[6],公式為

(4)

該公式中Qd和Qc可由文獻[13]獲得,Qsp和Qsw可由文獻[6]獲得.

應當指出，即使給出所需的工作頻率f0和基板的相關參數(εr,tanδ,H),單饋切角方形CPMSA與切角的物理尺寸也不能直接從公式(1)～(4)中計算得到. 為了解決這個問題,本文采用SVM在[f0,εr,tanδ,H]和[L,Lt]之間建立起非線性映射關系.

2支持向量機集成

SVM是Vapnik等人在1992年根據統計學習理論中結構風險最小化原則提出的,它是一種基于數據的機器學習方法,適合解決高維非線性問題的建模,因此，受到越來越多的重視[7].SVM的主要思想是通過非線性變換將樣本數據映射到一個高維的特征空間中,從而解決了原空間的非線性問題,而這個非線性特征映射是通過適當的核函數在算法中實現的,常見的核函數如下[14]:

1) 多項式核,得到的SVM是一個d階多項式分類器.

K(x,x′)=((x·x′)+c)dc≥0.

(5)

2) 高斯徑向基核,得到的SVM是一種徑向基函數分類器.

(6)

3)Sigmoid核,得到的SVM是一個兩層感知器,其隱層神經元的數目和算法都由算法自動確定.

K(x,x′)=tanh(λ(x·x′)+a)

λ>0, a<0.

(7)

近幾年,由于SVM需要樣本少、泛化能力強、擬合精度高等優點,已經有少量的文獻將其用于天線設計中[15-17],但關于集成學習在天線設計中的應用目前還未見報道. 集成學習主要是通過訓練、組合多個準確、有差異度的學習器,提高泛化能力和準確性;目前,國內外以決策樹、神經網絡等為基分類器的集成學習研究已經取得了很大的進展,但是對SVME的研究起步較晚,有少量的文獻研究了SVM作為分類機的選擇性集成,研究顯示,選擇性集成方法比傳統的集成學習方法Bagging和boosting有更好的分類效果[18]. 同神經網絡集成構成方法類似,SVME研究主要集中在兩個方面:一是如何選定集成中的個體網絡;二是個體網絡的輸出如何合成為網絡集成的輸出[19]. 提出了SVM作為回歸機的選擇性集成方法,由于SVM用不同的參數尋優方法和用同一種參數尋優方法均可以得到多組不同的最優參數組合值,而不同的組合值有不同的回歸預測效果,為了得到穩定且預測精度更好的SVM結構,采用基于BiPSO算法形成的選擇性SVME方法,通過PSO算法合理選擇組成SVME的各個預測精度較好的基本SVM,使個體間保持較大的差異度.

2.1　PSO算法的基本原理

PSO算法的標準速度位置更新公式為[20]:

vt+1=ω·vt+c1·rand()·(pt-xt)+

c2·rand()·(gt-xt) ,

(8)

xt+1=xt+vt+1.

(9)

式中: t是進化代數;xt和vt分別是當前粒子在第t次迭代時候的位置和速度;ω是慣性權值;c1,c2是加速因子,分別表示粒子的自我和社會認知能力,均是定值;pt表示個體極值的位置；gt表示全局極值的位置.

在PSO算法中,優化問題中所有可能解可以被看作是搜索空間中的一個位置,稱為粒子. 每個粒子都有一個相應的適應值,算法不僅記錄了粒子目前的位置,還記錄了到現在為止該粒子曾達到過最好適應值的位置和群體中所有粒子曾達到過最好適應值的位置. 所有粒子都有各自飛翔的方向和位移,由速度矢量v決定. PSO 初始化為一群隨機粒子,然后根據最優粒子的位置,粒子們在解空間中搜索,并通過上式迭代找到最優解.

2.2　基于BiPSO算法的SVME

集成問題首先要解決如何選取參與集成的個體. 為了找到一個合適的SVME的單饋切角方形圓極化的合成模型,經過多次試驗后發現選用高斯徑向基(Radial Basis Function, RBF)核函數有更好的預測效果. 針對支持向量機對核函數類型及參數擾動的敏感性,主要采用擾動學習器的模型參數法[21]構成集成個體. 現有的參數擾動方法就是選定一種核函數,改變既選定核函數所對應的最優參數組合,從而得到不同的分類預測效果. 通過實驗分析可以得知在上述核函數中, RBF核函數對這篇文章所研究的內容會取得相對較好的預測效果,因此在核函數的選擇中單個SVM個體的核函數均選擇RBF核函數,然后各個SVM通過采用不同的參數尋優方法,得到多組不同對的懲罰系數C和核系數g組合,這里參數尋優方法主要有交叉驗證法、粒子群算法、遺傳算法等. 為了保證選擇個體的差異性,隨機選擇上述參數尋優的方法,訓練產生40個不同參數組合的SVM個體,由于每個參數尋優方法每次均可以得到不同的參數組合值,因此構成了多個對應不同組參數的SVM個體.

假設已經訓練好n個SVM個體m1,m2,…,mn,利用這n個SVM組成的集成對求解問題建立映射關系. 采用PSO算法進行選擇性集成,即令PSO算法中的每一個粒子代表{m1,m2,…,mn}的一種集成,粒子空間的維數為SVM的數量n,這項研究選擇BiPSO算法實現選擇性SVME.

針對離散空間的優化問題,Kennedy和Eberhart提出了離散粒子群算法中的BiPSO算法[22],其中粒子的速度更新公式可以與式(8)相同,而位置每一維的取值為離散的0或者1,如果在某一維取值為1,表示對應的網絡個體參與集成;如果是0,則不參與集成,即

(10)

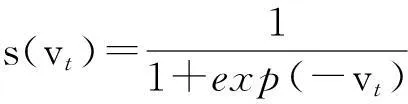
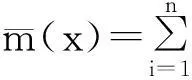
(11)

式中: αi對應于式(10)中的位置矢量,即位置取值為1的個體參與集成; ωi為每個參與集成的個體的權系數,大小為該SVM預測誤差的倒數.

3基于BiPSO 算法的選擇性SVME方法用于切角方形CPMSA的綜合建模

利用前面的基于BiPSO 算法的選擇性SVME方法對切角方形CPMSA進行綜合建模,即對于給定的基片的相關參數(εr,tanδ,H)和所需的工作頻率(f0),計算出切角單饋CPMSA的物理尺寸. 輸入樣本集合為[f0,εr,tanδ,H],相應的[L,Lt]作為輸出,訓練好的SVME在微帶天線相關參數與方形貼片的尺寸大小、切角大小之間分別建立起映射關系. SVM的訓練和測試用數據源于文獻[10]的實驗結果. 首先進行數據預處理,將數據統一歸一化在[0，1]之間,表1的第1到第4列給出了方形微帶天線的介質材料的相關屬性和對應的諧振頻率,第5、6列給出測量得到的達到圓極化效果的對應的物理尺寸,共列出了23個數據集,其中20個用于訓練SVME,最后三個用于測試SVME. PSO的粒子個數為30. 學習因子按照文獻[24]選取,即c1=2.8,c2=1.3,慣性權重ω從1線性變化到0.4[25],每次進化100代. 考慮到隨機性造成的影響,將程序運行20次,表中的結果是這10次的平均值. 表中第7、8列是本文得到的結果,第9、10列是ANN 訓練上述20個樣本數據得到的結果,第10、11列是單個SVM得到的結果. 表1中也給出了每種方法實測值與實驗值之間的絕對誤差的總和. 從中能夠看出,基于BiPSO的選擇性SVME的運行結果比ANN、單個SVM的運行結果誤差更小、更精確,說明本文所建立的SVME模型性能優于ANN和SVM的模型.

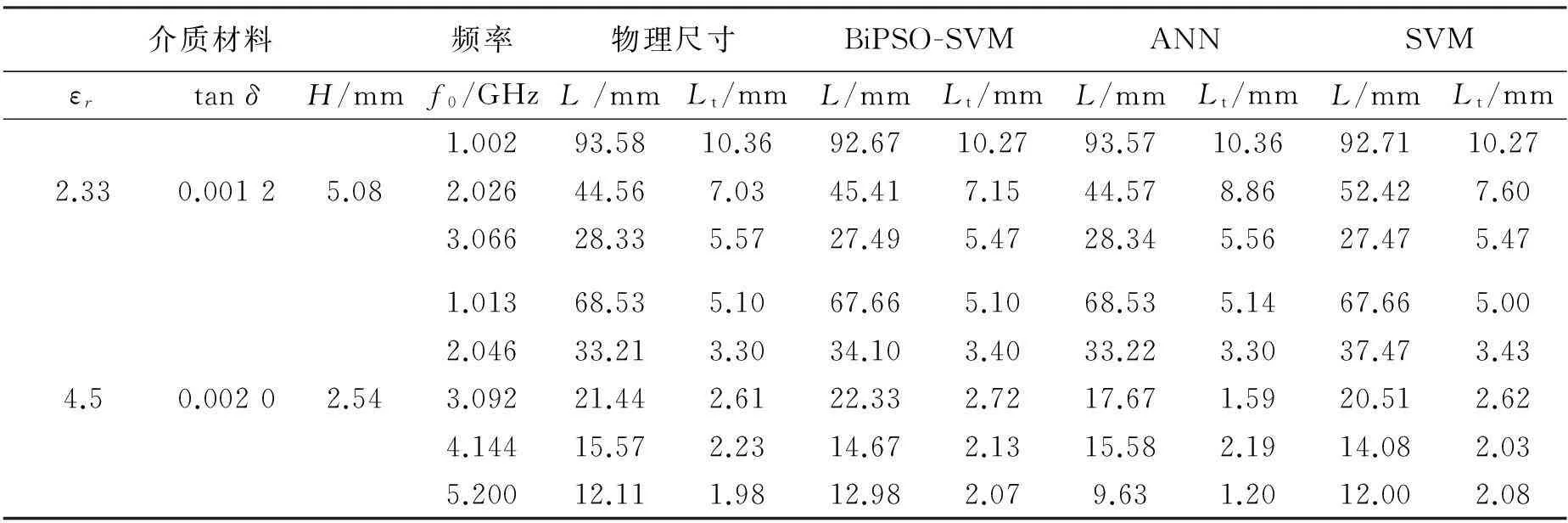
表1　方形圓極化微帶天線的綜合模型

(續表)

為進一步驗證基于BiPSO的SVME對切角方形CPMSA建模的有效性和可靠性,表2給出了本文所用方法訓練上述20個樣本數據得到的測試數據與實測數據的差值和文獻[10]中用3 500個訓練數據得到的預測值與實測值的差值比較,從中選取5個測試數據進行對比,同樣,最終結果是取程序運行20次的輸出結果的平均值. 文獻[10]中用于合成模型中的網絡結構是4×4×24×8×2,隱層用了正切S形激活函數,同時輸出層用了線性激活函數,最大的允許訓練次數為1 000. 從表2中可以看出,本文方法得出的結果比文獻[10]中的ANN方法建立的模型預測的結果誤差更小、更接近于實測值,且減輕了需要根據經驗公式計算而得到大量訓練數據的繁重計算工作,節省了實測所需的昂貴的成本和時間. 采用HFSS電磁仿真軟件驗證了相應的軸比均小于1 dB,和得到的測量結果之間存在良好的一致性,證明了該方形CPMSA可以通過基于BiPSO的SVME模型綜合得到.

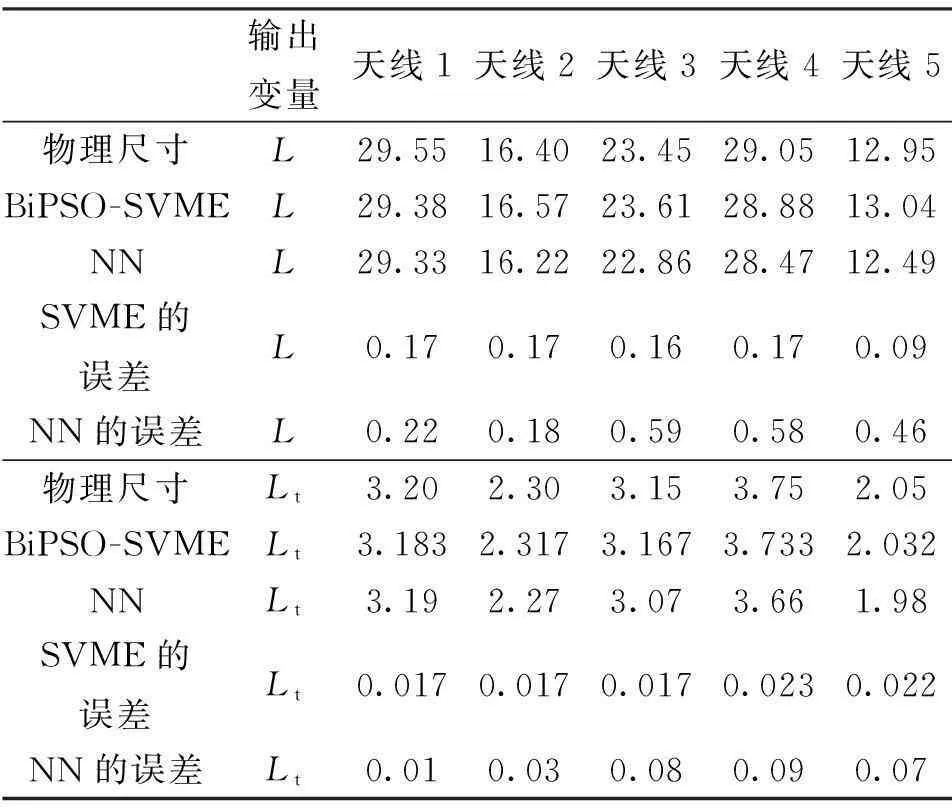
表2　與用傳統方法得到的理論值與實測值之間的絕對誤差的比較　mm

4結論

將基于BiPSO算法的SVME成功地引入了單饋切角方形CPMSA的綜合建模問題中,通過和ANN、單個SVM以及現有文獻預測結果對比可以看出,基于BiPSO算法的SVME有更好的預測精度,提高了穩定性、魯棒性和有效性,節省了大量數據的計算時間和實測所需的昂貴成本,該模型優于此問題的已有結論,表明它可以被用于設計單饋切角方形CPMSA.

參考文獻

[1] HOWELL J Q. Microstrip antennas[J]. IEEE Transactions on Antennas and Propagation, 1975, 23(1): 90-93.

[2] WONG K L. Compact and Broadband Microstrip Antennas [M]. New York: John Wiley & Sons, 2004.

[3]姜文, 張揚, 洪濤, 等. 小型化低雷達散射截面圓極化微帶天線研究[J]. 電波科學學報, 2013, 28(5): 810-814.

JIANG Wen, ZHANG Yang, HONG Tao, et al. Novel miniaturized and low RCS circularly polarized microstrip antenna[J]. Chinese Journal of Radio Science, 2013, 28(5):810-814. (in Chinese)

[4] 錢祖平, 劉宗全, 馮衛華, 等. 一種新型寬帶寬波束圓極化微帶天線的設計[J]. 電波科學學報, 2012, 26(6): 1170-1175.

QIAN Zuping, LIU Zongquan, FENG Weihua, et al. Design of a new circularly-polarized broadband microstrip antenna with broad beamwidth[J]. Chinese Journal of Radio Science, 2012, 26(6): 1170-1175. (in Chinese)

[5] HANEISHI M, YOSHIDA S. A design method of circularly polarized rectangular microstrip antenna by one-point feed[J]. Electronics and Communications in Japan (Part I: Communications), 1981, 64(4): 46-54.

[6] JACKSON D R, LONG S A, WILLIAMS J T, et al. Computer-aided design of rectangular microstrip antennas [J]. Advances in Microstrip and Printed Antennas, 1997: 223-270.

[7] 張學工. 關于統計學習理論與支持向量機[J]. 自動化學報, 2000, 26 (1): 32-42.

ZHANG Xuegong. Introduction to statistical learning theory and support vector machines[J]. Acta Automation Sinica, 2000, 26 (1): 32-42.(in Chinese)

[8] 周志華, 陳世福. 神經網絡集成[J]. 計算機學報, 2002, 25(1): 1-8.

ZHOU Zhihua, CHEN Shifu. Neural network ensemble [J]. Chinese Journal of Computers, 2002, 25(1): 1-8. (in Chinese)

[9] 蔡俊偉, 胡壽松, 陶洪峰. 基于選擇性支持向量機集成的混沌時間序列預測[J]. 物理學報, 2008, 56(12): 6820-6827.

CAI Junwei, HU Shousong, TAO Hongfeng. Prediction of chaotic time series based on selective support vector machine ensemble[J]. Journal of Physics, 2008, 56(12): 6820-6827. (in Chinese)

[10]WANG Z, FANG S, WANG Q, et al. An ANN-based synthesis model for the single-feed circularly-polarized square microstrip antenna with truncated corners[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(12): 5989-5992.

[11]KARA M. The resonant frequency of rectangular microstrip antenna elements with various substrate thicknesses[J]. Microwave and Optical Technology Letters, 1996, 11(2): 55-59.

[12]HAMMERSTAD E O. Equations for microstrip circuit design[C]//5th European Microwave Conference. Hamburg: IEEE, 1975: 268-272.

[13]JAMES J R, HALL P S, WOOD C. Microstrip Antenna Theory and Design[M]. London: Peregrinus, 1981.

[14]瑞明. 支持向量機理論及其應用分析[M]. 北京: 中國電力出版社, 2007.

[15]MIN G, FENG Y. Calculation of the characteristic impedance of TEM horn antenna using support vector machine[C]//2010 International Conference on Microwave and Millimeter Wave Technology, 2010: 895-897.

[16]JACOBS J P, KOZIEL S, OGURTSOV S. Computationally efficient multi-fidelity Bayesian support vector regression modeling of planar antenna input characteristics[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(2): 980-984.

[17]李壽林, 李秀萍, 張鷹. 支持向量機回歸法在天線設計中的應用[J]. 電子器件, 2007, (4): 1285-1288.

LI Shoulin, LI Xiuping, ZHANG Ying. Application of support vector machine regression method in the design of antenna[J]. Electronic Devices, 2007, (4): 1285-1288. (in Chinese)

[18]李燁. 基于支持向量機的集成學習研究[D]. 上海: 上海交通大學, 2007.

LI Ye. Ensemble Learning Based on Support Vector Machins[D]. Shanghai: Shanghai Jiao Tong University, 2007. (in Chinese)

[19]田雨波, 董躍. 基于神經網絡集成的微帶天線諧振頻率建模[J]. 電波科學學報, 2009, 24(4): 610-616.

TIAN Yubo, DONG Yue. Modeling resonant frequency of microstrip antenna based on neural network ensemble [J].Chinese Journal of Radio Science,2009,24(4): 610-616. (in Chinese)

[20]田雨波, 李正強, 王建華. 矩形微帶天線諧振頻率的粒子群神經網絡建模[J]. 微波學報, 2009, 25(5): 45-50.

TIAN Yubo, LI Zhengqiang, WANG Jianhua. Model resonant frequency of rectangular microstrip antenna based on particle swarm neural network[J]. Journal of Microwave, 2009, 25(5): 45-50. (in Chinese)

[21]程麗麗. 支持向量機集成學習算法研究[D]. 哈爾濱: 哈爾濱工程大學, 2009.

CHENG Lili. Research on Support Vector Machin ensemble Learning Algorithm[D]. Harbin: Harbin Engineering University, 2009. (in Chinese)

[22]KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm[C]//IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando: IEEE, 1997, 5: 4104-4108.

[23]劉擎超, 朱玉全, 陳耿. 基于PSO拓展的多分類器加權集成方法[J]. 計算機工程, 2012, 38(7): 174-176.

LIU Qingchao, ZHU Yuquan, CHEN Geng. Multiple classifiers weighted integration method based on particle swarm optimization expanded[J]. Computer Engineering, 2012, 38(7):174-176. (in Chinese)

[24]張麗平. 粒子群優化算法的理論及實踐[D]. 杭州: 浙江大學, 2005.

ZHANG Liping. The Theorem and Practice upon the Particle Swarm Optimization Algorithm[D]. Hangzhou: Zhejiang University, 2005. (in Chinese)

[25]SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington: IEEE, 1999.

田雨波(1971-),男(滿),遼寧人,教授,博士,碩士生導師,2009年到美國UCLA做訪問學者,主要研究方向為計算智能及其電磁學應用．

孫菲艷(1991-),女,江蘇人,碩士研究生,研究方向為智能信息處理與系統．

任作琳(1991-),女,遼寧人,碩士研究生,研究方向為智能優化算法.

李昌澤, 童創明, 齊立輝, 等. 三類新型隨機粗糙面模型的快速散射特性分析[J]. 電波科學學報，2015，30(6)：1093-1101. doi: 10.13443/j.cjors. 2015012901

LI Changze, TONG Chuangming, QI Lihui, et al. Analysis on fast electromagnetic scattering characteristics for three novel randomly rough surface models[J]. Chinese Journal of Radio Science，2015，30(6)：1093-1101. (in Chinese). doi: 10.13443/j.cjors. 2015012901

Design of circularly-polarized microstrip antenna

by SVM ensemble

TIAN YuboSUN FeiyanREN Zuolin

(SchoolofElectronicsandInformation,JiangsuUniversityofScienceand

Technology,Zhenjiang212003,China)

AbstractA large deal of calculating data and complex structure is needed when design circularly-polarized microstrip antenna (CPMSA) with artificial neural network. To solve this problem, a synthesis model based on SVM ensemble (SVME) is proposed for the design of single-feed CPSMA with truncated corners. This method was based on the features of high fitting precision, simple structure, and the strong generalization ability of the support vector machine (SVM). The basic idea of the method was to optimally select differential SVMs to construct SVME with the aid of binary particle swarm optimization (BiPSO) algorithm. The model is validated by comparing its results with artificial neural network and a single SVM. Experiments show that the method is effective. It may improve the generalization ability of SVM and reduce the prediction error, and this model is superior to the problem of existing conclusions.

Key wordscircularly-polarized; microstrip antenna (MSA); cutting angle; particle swarm optimization (PSO); support vector machine ensemble (SVME)

作者簡介

收稿日期：2014-12-29

中圖分類號TN820

文獻標志碼A

文章編號1005-0388(2015)06-1086-07