車載雷達穩定轉臺伺服系統有限時間積分滑模控制
馮瑗瑗,華光輝
(1.中國船舶重工集團公司第七二四研究所,南京 211153;2.中國電力科學研究院,南京 210003)
車載雷達穩定轉臺伺服系統有限時間積分滑模控制
馮瑗瑗1,華光輝2
(1.中國船舶重工集團公司第七二四研究所,南京 211153;2.中國電力科學研究院,南京 210003)
摘要:應用有限時間穩定和積分滑模控制理論,提出了一種響應速度快、具備較強抗干擾能力的車載雷達穩定轉臺伺服系統新型控制方法。建立了被控對象和控制系統的四階數學模型,基于MATLAB開展了計算機仿真實驗,驗證了有限時間積分滑模控制效果,為工程應用奠定了基礎。
關鍵詞:車載雷達;伺服控制系統;有限時間穩定;積分滑模;計算機仿真
0引言
車載雷達穩定轉臺是一個機械傳動裝置。它可以使安裝在車輛上的雷達天線不受車輛運動的影響,在車輛出現傾斜或轉向時,讓天線始終保持某一個給定的方向和傾角,從而保持雷達的正常工作。穩定轉臺是車載雷達的重要組成部分,對于發現目標、跟蹤目標以及測量目標的位置、速度等參數都起著重要作用。隨著現代雷達技術的不斷發展,車載雷達對穩定轉臺伺服控制系統也提出了越來越高的技術需求[1]。伺服控制除了常規的PID控制技術外,還有智能PID控制、智能控制、自適應控制、滑模控制等[2]。
滑模控制系統的動態性能主要取決于滑模面的選擇。傳統的滑模控制器設計的滑模面具有線性的形式,只能保證系統狀態在滑模面上漸近收斂。為了改善系統的收斂特性和抗擾動性能,國內外學者結合有限時間控制理論提出了很多解決辦法,使系統狀態達到滑模面后可在有限時間內滑動到原點[3]。
文獻[4]提出一種積分滑模控制方法,并通過仿真證明在伺服系統出現參數變化和外部干擾時,積分滑模控制系統有很高的動態性能和很好的魯棒性。文獻[5]指出對不確定和擾動的系統進行控制時,有限時間穩定系統與一般漸近收斂的無限時間穩定系統相比,在原點附近具有更快的收斂性,而且具有更好的魯棒性和抗干擾能力。文獻[6]從最優控制的角度設計了基于有限時間收斂的新型滑模控制器,可以使系統獲得較好的魯棒性。文獻[7]設計了傳統滑模變結構控制器,通過計算機仿真方式與經典PID控制方法進行了對比,證明了滑模控制的控制效果。
本文在傳統滑模控制的基礎上,根據有限時間控制理論和積分滑模控制,提出一種新的有限時間滑模控制器設計方法。它可以提高閉環系統狀態在滑模面上的收斂速度,使穩定轉臺伺服系統快速收斂。
1被控對象的機理模型
1.1 伺服系統三質量數學模型
本文所研究的車載雷達為兩軸穩定轉臺,雷達天線的目標給定角度通過方位控制通道和俯仰控制通道驅使雷達穩定轉臺在方位和俯仰兩個自由度上旋轉,共同作用使雷達天線指向預定方向。以方位控制為例,建立車載雷達穩定轉臺方位控制系統數學模型[7]。
為保證穩定轉臺的控制精度,在此對伺服系統建立三質量數學模型,即由包括電機、純慣性負載以及連接二者的等效傳遞機構三部分組成,其數學模型如圖1所示。
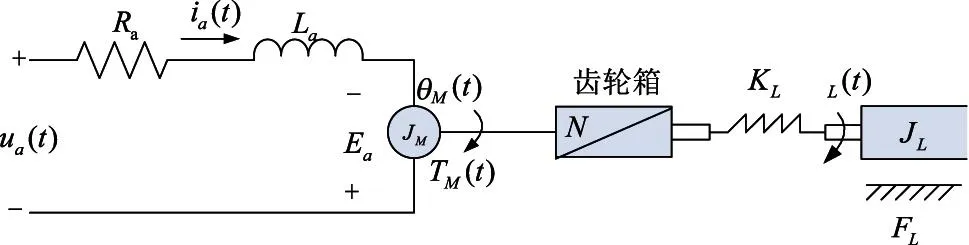
圖1 電機通過彈性軸驅動負載的組合模型
然后可以列出方程:
(1)
(2)
TM=KTIa
(3)
(4)
(5)
(6)
式中,Ua是加在電機電樞兩端電壓,Ea是電機反電動勢,Ia是電樞電流,Ra是電機的電樞電阻,La是電機的電樞電感,Km是電機反電動勢系數,θM電機軸的角位移,TM是電機力矩,KT是電機力矩常數,JM是電機電樞轉動慣量,T是彈性軸中的力矩(即作用于負載上的力矩),N是齒輪箱減速比,KL是彈性軸的剛性,θL是傳動架的角位移,JL是負載慣量,FL是黏性摩擦常數。
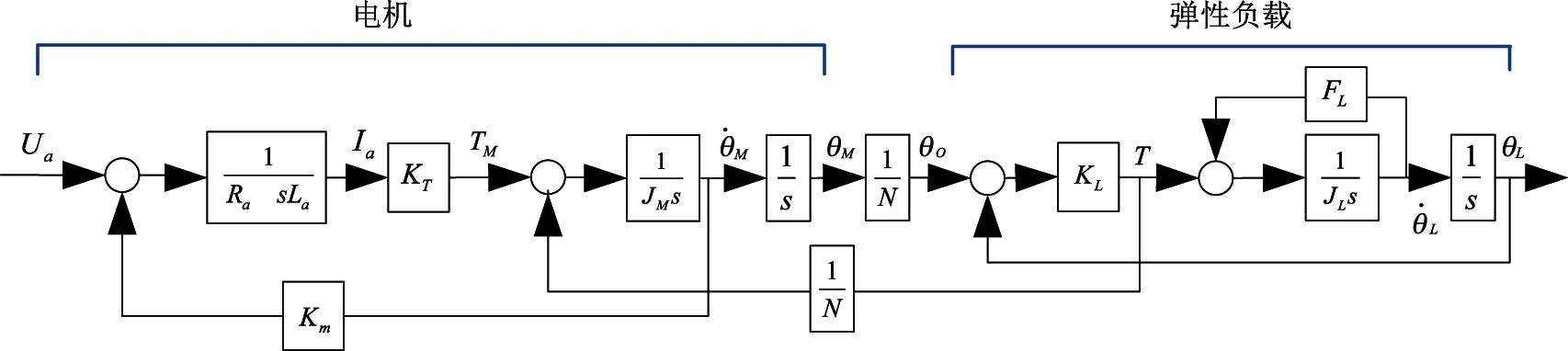
圖2 系統模型的方框圖
1.2 穩定轉臺伺服系統的摩擦模型
本文采用一種如圖3所示的Stribeck摩擦模型。由于在不同的階段物體接觸面之間的相對運動速度也不一樣,因此在穩態時摩擦力表現為物體相對速度的函數[8]。該模型給出了在不同摩擦階段摩擦力與速度之間的關系。
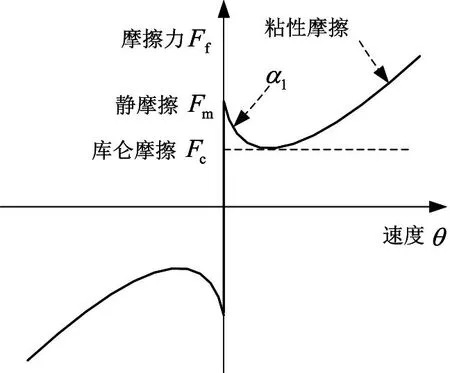
圖3 Stribeck摩擦模型
(7)
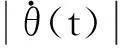
(8)
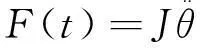
(9)
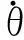
1.3 伺服系統PID控制
伺服控制常用的控制方法是PID控制,而且一般采用位置和速度雙閉環控制。經過控制參數尋優,可以取得較理想的階躍響應曲線如圖4所示。
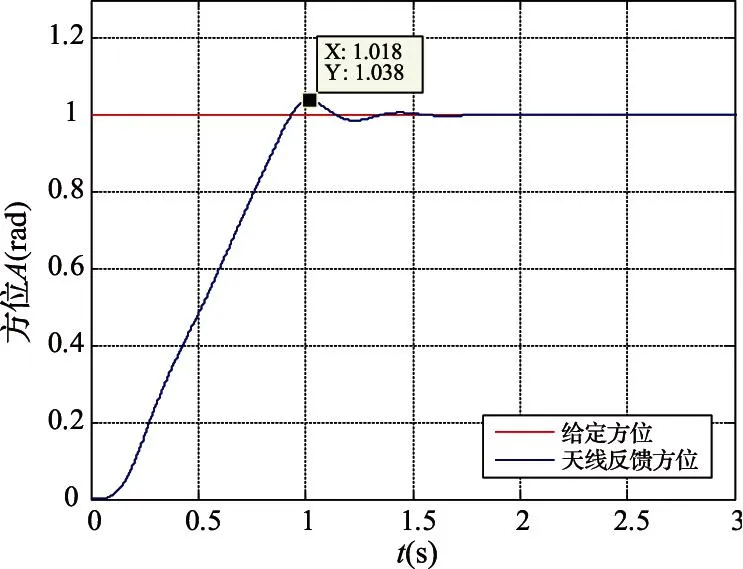
圖4 PID控制位置階躍響應曲線
可以看出,在對被控對象進行精確建模的情況下,傳統PID控制能夠取得較為理想的控制效果。但是,當系統參數發生變化或者外部出現干擾時,其超調量、過渡時間等性能指標會顯著下降,詳細研究內容見參考文獻[7]。
2有限時間穩定性相關理論
2.1 有限時間穩定性定義
定義1[9]考慮如下系統:
(10)

2.2 積分鏈系統有限時間收斂算法
引理1[9]假設存在φ1,φ2,…,φn>0使得多項式sn+φnsn-1+…+φ2s+φ1是Hurwitz的,考慮如下系統:
(11)
存在μ∈(0,1),使得?α∈(1-μ,1),對于上述系統控制器設計如下:
(12)
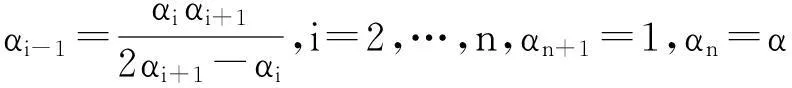
有限時間控制器中帶有分數冪項。這一特點使得有限時間閉環控制系統與非有限時間閉環控制系統相比,前者具有更好的魯棒性和抗擾動性能[5]。
2.3 有限時間積分滑模面設計
本文定義積分滑模面如下[10-11]:
(13)
其中控制率u已在引理1中給出。t0是初始時間,容易推出t=t0時,s(t0)=0。因此,系統從初始時刻起就在滑模面上。
3伺服系統有限時間積分滑模控制器設計
設
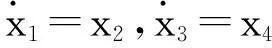
(14)
其中

此系統為單輸入系統,其系數矩陣的秩等于4,屬于非奇異矩陣,系統完全能控。
為了構造滑模函數,設
(15)
式中
(16)
(17)
(18)
(19)
被控對象階數n=4,設α=4/5,則滑模面函數為
(20)
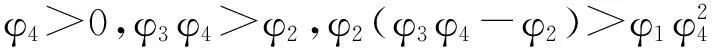
滑模面函數的導數為
(21)
其中

(23)
4有限時間積分滑模控制器仿真實驗
針對前文所給出的車載雷達穩定轉臺伺服系統被控對象參數,根據有限時間積分滑模控制器設計方法,基于MATLAB仿真開展相關實驗,驗證控制算法的有效性和優越性[12-15]。
取φ1=20 000,φ2=16 000,φ3=4 000,φ4=300,k=100,ε=20,天線反饋方位在有限時間內跟蹤給定方位,而且能夠較好地跟蹤給定值,如圖5所示。
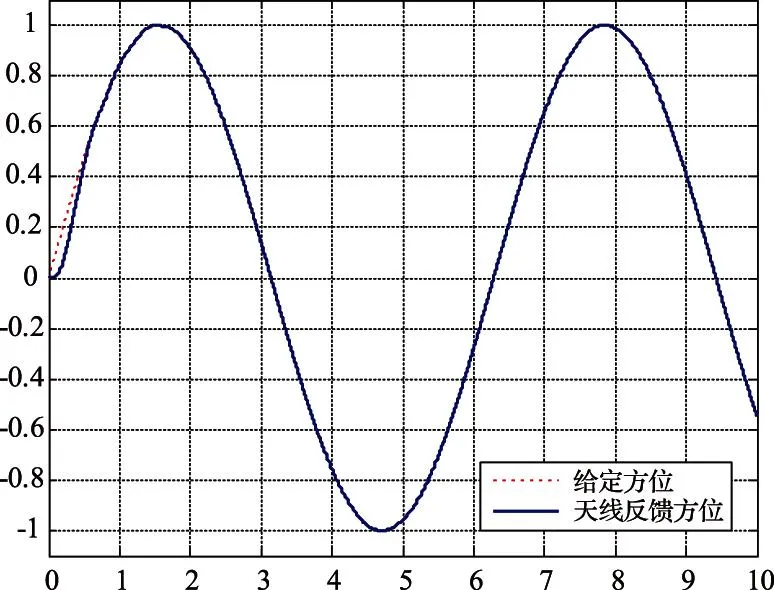
圖5 位置給定與天線位置跟蹤曲線
此時控制器u的輸出如圖6所示。可見除了在啟動階段有幾次振蕩之外,控制量輸出已經基本沒有抖振現象,說明該控制器對系統抖振也具有較強的抑制作用。
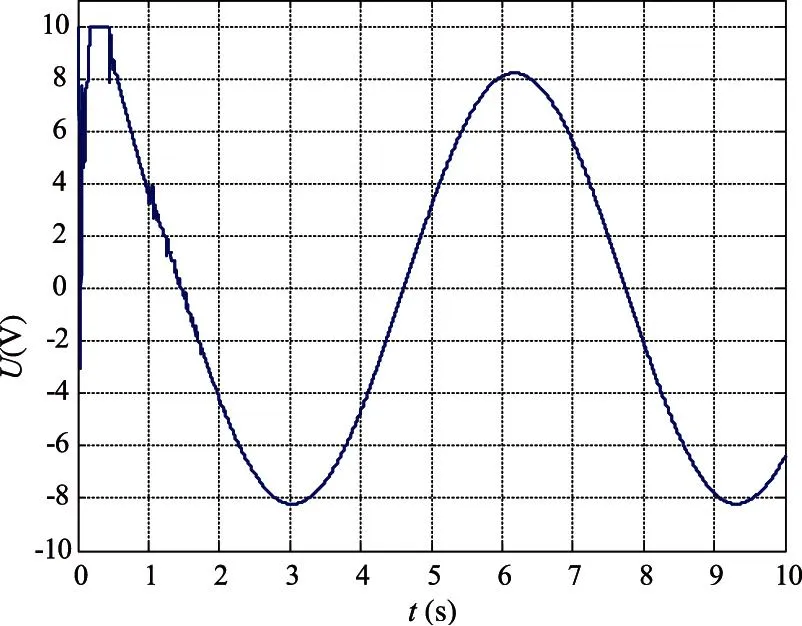
圖6 控制量輸出曲線
方位給定與天線反饋位置之差e的曲線如圖7所示。可見時間在1s時,誤差收斂到0,表明系統能夠在1s的有限時間內有效地跟蹤參考曲線。
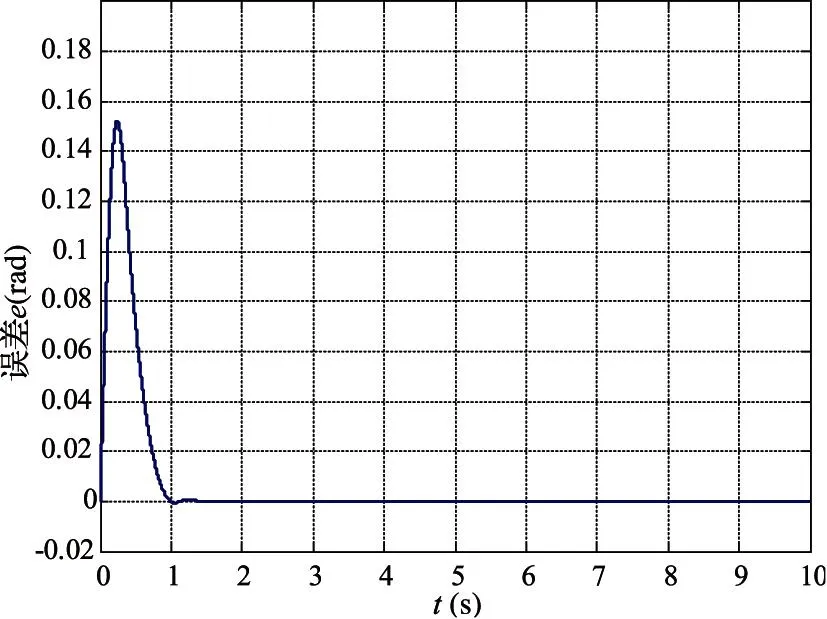
圖7 位置跟蹤誤差曲線
開展伺服系統內部參數變化對比試驗,負載慣量由原先的150kg·m2變為250 kg·m2,變化前后的階躍響應曲線如圖8所示。可見兩條曲線相差很少,基本保持一致。

圖8 負載慣量發生變化時方位跟蹤曲線
當粘性摩擦系數FL發生了變化,假設由原來的1500N·m·s/rad增大為3000N·m·s/rad,變化前后的階躍響應曲線如圖9所示,可見變化后超調量有所增加,但是基本保持一致。
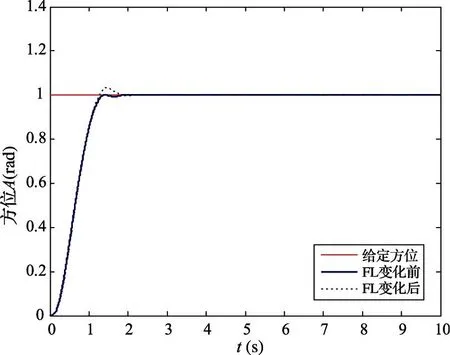
圖9 粘性摩擦系數發生變化時方位跟蹤曲線
利用Stribeck摩擦模型來模擬控制參數時變的伺服控制系統,完成車載雷達穩定轉臺方位階躍試驗,曲線如圖10所示。可見針對摩擦系數時變系統,所設計控制系統是收斂的,而且動態、靜態控制效果也同樣滿足設計要求。
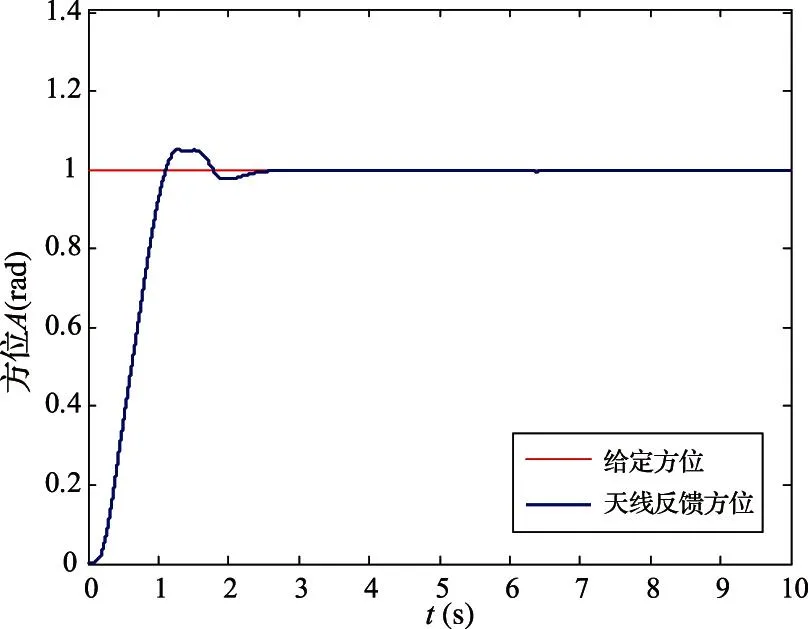
圖10 摩擦系數時變系統方位跟蹤曲線
當在負載力矩處疊加TO=-1000 N·m的持續外部干擾時,通過仿真試驗可以得到如圖11的對比曲線。可見增加外部干擾后超調量有所增加,但系統能夠在有限時間內快速穩定。
在實際工作中,兩軸穩定轉臺由于天線姿態變換、機械連接、加工工藝、信號不同步等因素,方位和俯仰兩軸之間存在著交叉耦合[16-17]。圖12在正弦給定的基礎上疊加方波信號,模擬方位控制閉環做扇掃控制的同時出現俯仰通道的耦合信息的情況,雷達天線方位能夠快速跟蹤給定信號,具有較好的解耦控制能力。

圖11 系統出現外部干擾時方位跟蹤曲線
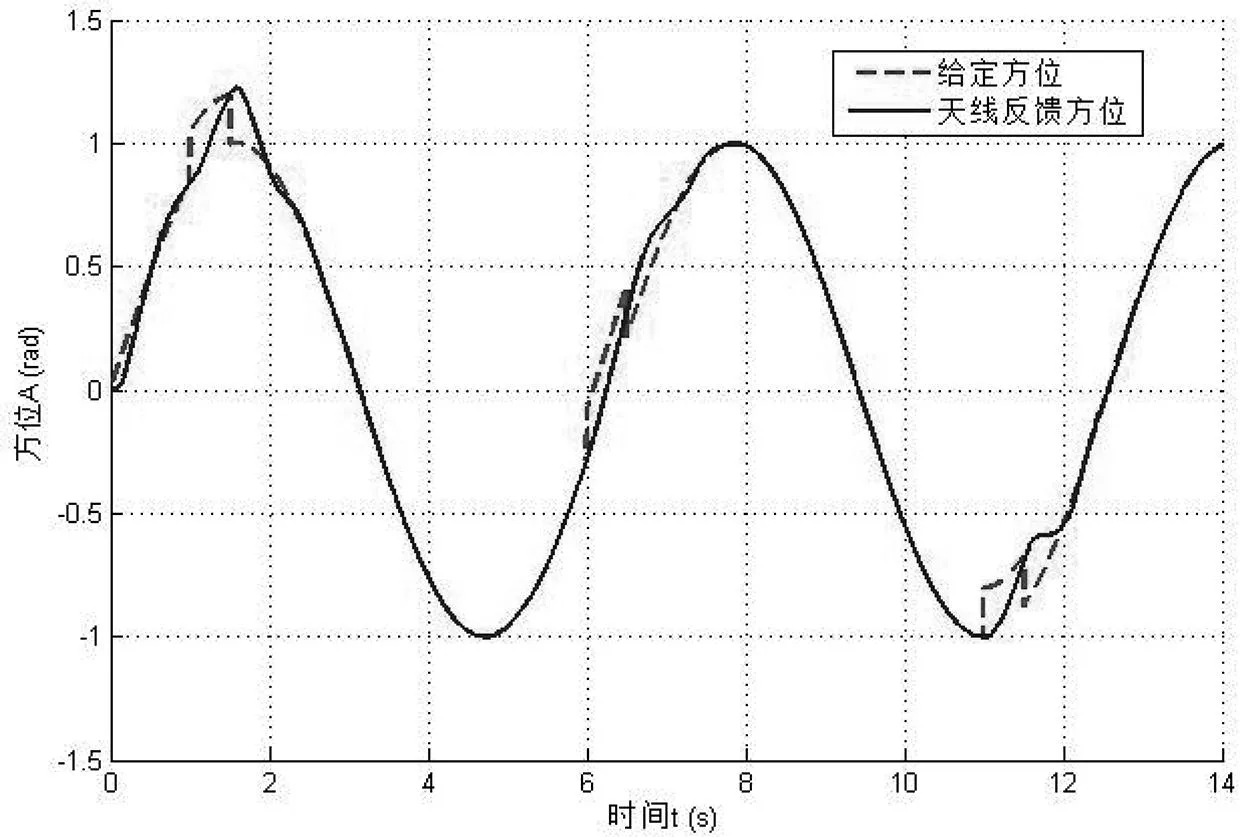
圖12 兩軸交叉耦合時方位跟蹤曲線
通過以上計算機仿真實驗可以得知,本文設計的有限時間積分滑模控制器能夠有效抑制系統抖振,而且在出現參數變化、外部擾動、交叉耦合時依然具有良好的魯棒性,控制效果良好。
5結束語
本文將伺服控制單元和天線負載合在一起看作被控對象,建立了車載雷達穩定轉臺的三質量數學模型,提出了控制對象的四階傳遞函數,并建立了狀態方程。根據有限時間穩定和積分滑模控制理論,給出了一種新的有限時間收斂的滑模控制器設計方法,并結合Stribeck摩擦模型對伺服控制方法進行了深入研究。通過MATLAB仿真證明,相比傳統的PID控制器,本文設計的有限時間積分滑模控制器具有更強的魯棒性,能夠有效提高收斂速度,保證系統快速響應。
參考文獻:
[1]劉世挺.雷達伺服控制技術的新發展[J].火控雷達技術,2002,27(1): 33-35.
[2]董彩云.基于滑模變結構控制的電液伺服系統及實驗研究[D].秦皇島: 燕山大學,2007.
[3]丁世宏,李世華.有限時間控制問題綜述[J].控制與決策,2011,26(2): 161-169.
[4]湯青波,張國新,何學文.電液伺服系統的積分滑模控制[J].機床與液壓,2011,39(9): 48-50.
[5]劉慧賢,丁世宏,李世華,等.永磁同步電機位置伺服系統的有限時間控制[J].電機與控制學報,2009,13(3): 424-430.
[6]SalahLaghrouche,FranckPlestan,AlainGlumineau.Higherorderslidingmodecontrolbasedonintegralslidingmode[J].Automatic,2007,43(3): 531-537.
[7]馮瑗瑗,丁鋒.車載雷達穩定轉臺伺服控制系統仿真研究[J].機電信息,2014,6: 144-146
[8]張國柱,陳杰,李志平.直線電機伺服系統的自適應模糊摩擦補償[J].電機與控制學報,2009,13(1): 154-160.
[9]劉慧賢,王釗,李世華.永磁同步電機位置伺服系統的有限時間位置控制[J].系統科學與數學,2010,30(6): 721-732.
[10]Zong Q,Zhao Z S,Zhang J.Higher order sliding mode control with self-tuning law based on integral sliding mode[J].IET Control Theory and Applications,2010,4(7): 1282-1289.
[11]趙占山,張靜,孫連坤,等.有限時間收斂的滑模自適應控制器設計[J].山東大學學報,2012,42(4): 74-78.
[12]鄒云飛,劉金琨,王宗學.轉臺伺服系統滑模變結構控制器的設計與仿真研究[J].計算機仿真,2002,19(2):74-76.
[13]劉金琨.滑模變結構控制MATLAB仿真(第2版)[M].北京: 清華大學出版社,2012.
[14]陳志梅,王貞艷,張井崗.滑模變結構控制理論及應用[M].北京: 電子工業出版社,2012.
[15]陳杰,李志平,張國柱.不確定非線性系統的高階滑模控制器設計[J].控制理論與應用,2010,27(5): 563-569.
[16]鮑文亮,黃顯林,盧鴻謙.多框架光電平臺動力學建模及耦合分析[J].哈爾濱工程大學學報,2009,30(8): 893-896
[17]王俊峰,左增宏.單通道單脈沖自跟蹤系統交叉耦合分析[J].飛行器測控學報,2009,28(3): 30-33
Finite-time integral sliding mode control of servo system for
vehicle-borne radar stabilizing rotary platform
FENG Yuan-yuan1, HUA Guang-hui2
(1. No.724 Research Institute of CSIC, Nanjing 211153;
2. China Electric Power Research Institute, Nanjing 210003)
Abstract:A novel control method of the servo system for the vehicle-borne radar stabilizing rotary platform with fast response and strong anti-jamming capability is proposed, applying the theory of the finite-time stability and the integral sliding mode (ISM) control. A four-order mathematical model of the controlled object and the control system is established, and the computer simulation tests are carried out based on the MATLAB, verifying the effect of the finite-time ISM control, and laying the foundation of engineering application.
Keywords:vehicle-borne radar; servo control system; finite-time stability; ISM; computer simulation
中圖分類號:TN820.3
文獻標志碼:A
文章編號:1009-0401(2015)04-0054-06
作者簡介:馮瑗瑗(1984-),女,工程師,研究方向:雷達伺服系統控制;華光輝(1983-),男,高級工程師,研究方向:新能源發電技術、電機控制技術。
收稿日期:2015-07-20;修回日期:2015-07-25

