收入差距測度和分解的新方法
李群峰
(河南師范大學 商學院,河南新鄉453007)
0 引言
對于收入差距成因的研究而言,當前國內大部分學者往往通過某個度量收入差距的統計指標(如洛侖茲曲線、基尼系數和泰爾熵指數等)利用回歸模型進行成因分解,通過回歸系數的大小來判別某些影響因素對收入差距成因的貢獻度。該類方法雖然具有直觀容易理解的優點,但是缺點也顯而易見:(1)基尼系數和泰爾熵指數等單個統計指標從本質上講是對收入分布的總結性描述,包含的信息量有限,不能像收入分布密度函數那樣包含更為全面的信息,因而無法對復雜的收入分布做出更細致的刻畫;(2)在對影響收入分布的諸多因素進行成因分解時,基于回歸方法對單個統計指標的分解只是反映收入分布的一個側面,無法對整個收入分布變化進行描述,在實際應用上具有較大的局限性;(3)成因分解時所使用的回歸模型在模型構建時隨意性較大,如果模型的選擇和解釋變量設定有誤,不能描述收入形成的原因,那么基于回歸結果的成因分解必定存在偏誤。
針對傳統收入差距分解方法所存在的以上缺陷,本文提出能夠準確分解收入分布差異并具體測度其影響因素變化對收入差距貢獻度的新方法。該方法先利用“反事實分析方法”和半參統計方法構造并估計整個收入分布函數的“反事實”分布,將收入分布的差異(如分位數和方差)分解為收入組成效應和結構效應,再利用Firpo(2007)構造的RIF函數可以將以上效應表示成無條件分位數偏效應的特性,進行RIF回歸分解出各解釋變量對被解釋變量的影響,從而得到個解釋變量變化對于整體收入分布變動的具體貢獻度[1]。
1 反事實收入分布的構建與RIF成因分解
1.1 反事實收入分布密度函數的構建與估計
反事實分析法最先由諾貝爾經濟學獲得者Fogel(1964)在考察19世紀美國鐵路與美國經濟增長的關系提出,討論了假如鐵路從來就不存在,美國的經濟增長率會是多少,以此來估計鐵路對美國經濟增長的貢獻度。從統計的角度而言,反事實分布本質上是給定解釋變量之后收入變量的條件分布。在判別某種影響因素對收入分布的變化究竟有多大的貢獻時,我們可以借用反事實分析法的思路,通過分析假如某種因素不存在或者僅有某種因素發揮作用時,比較收入分布的變化進而發現對其起關鍵作用的因素。本文借助Powell(2010)提出的重置權重函數法構造反事實收入分布,該思路可以從圖形上直接識別收入分布變遷的原因,因而給下一步的成因分解帶來極大的便利[2]。針對之前所指出的完全非參和純粹參數方法的缺陷,本文對收入密度函數進行估計采用了半參數模型。
具體而言,首先在核密度估計量中引入與每一觀測值相關的樣本權重,形成如下加權核密度估計:
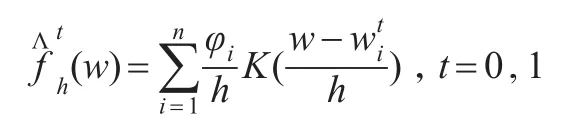
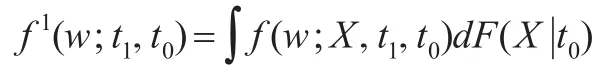
接著引入重置權重函數,通過變換特征分布將反事實收入分布作為t=1時期收入分布的重置加權形式。

通過以上思路,我們利用重置加權函數即可構造出所需要的反事實收入分布。
1.2 基于RIF映射函數的收入分布分解
之前研究者在對收入差距成因進行分解時,往往針對收入差距的衡量指標(基尼系數、泰爾指數、廣義嫡指數和變異系數)利用回歸模型進行成因分解,通過回歸系數的大小來判別某些影響因素對收入差距成因的貢獻度,卻很少有人關注包含信息量廣大的收入分布密度函數[3]。實際上,基于“反事實”收入分布的成因分解可以從整個收入分布上刻畫收入差距,還從圖形直觀發現收入差距的擴大的原因,并通過函數變換將收入密度函數轉化為衡量不平等的單一統計指標,如基尼系數和泰爾指數等,使得某個特定的收入差距衡量指標可以從收入分布密度函數的分解中得到,具有應用范圍更廣的優勢。因而本文在收入差距成因進行分解時,采用“反事實”收入分布和RIF回歸相結合的新分解方法,將收入分布的差異分解為收入組成效應和結構效應,基于RIF回歸分解出各解釋變量對被解釋變量的影響,從而得到解釋變量變化對于整體收入分布變動的貢獻度。具體過程如下:
假設t時期收入分布可以表示為Ft(yt),其中 y為勞動者收入,v(F)代表某一收入分布的分位數,t=0,1分別代表兩個不同時期,則v(F1-F0)即為兩時期在該分位數上的收入差距。Fc為反事實狀態的收入函數分布,即假設在t=1時期勞動者所在勞動力市場的特點(如平均受教育水平等)仍在t=0時期水平,而收入結構變遷到t=1時期情況下的收入。這樣,兩時期的收入差距v(F1)-v(F0)進行如下分解:
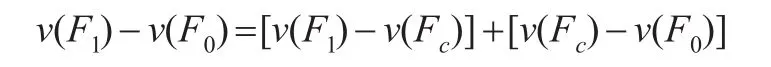
其中,[v(F1)-v(Fc)]為收入組成效應,是由于勞動者所在勞動力市場特點變化造成的收入分布的變化,如勞動者整體平均教育水平比例提高造成的變化;[v(Fc)-v(F0)]為收入結構效應,是由于對不同勞動力個體特點的收入回報變化,如年齡、職業和行業回報率提高等造成的收入分布的變化。

在具體計算時,上式的分解結果可以分三步進行。首先構建無條件分位回歸模型對
RIF(qτ,y,Fy)進行估計;得到RIF的一致估計后,用重置權重法方法構造反事實分布將收入分布差異分解為勞動力組成效應和工資結構效應;最后根據RIF函數的特性利用加權最小二乘分解各解釋變量對勞動力組成效應和工資結構效應的貢獻度。
2 實證研究
在本研究中,我們使用國家統計局城鎮居民入戶調查數據(1999年和2012年),所使用樣本數分別為23075和30158,選取年齡、性別、受教育程度、工作經驗、所在行業、職業、地域和收入等指標進行研究。在具體計算時,為了便于不同年份之間的比較,將2 012年的城鎮居民收入以1999年為基準進行折算。使用以上數據,采用半參核密度法繪制1999年和2012年的的收入分布圖,以及年齡、受教育程度、工作經驗和所在行業等指標等處在1999年而各種收入回報率在2012年水平上的反事實收入分布圖(圖1中2012C lgw)。
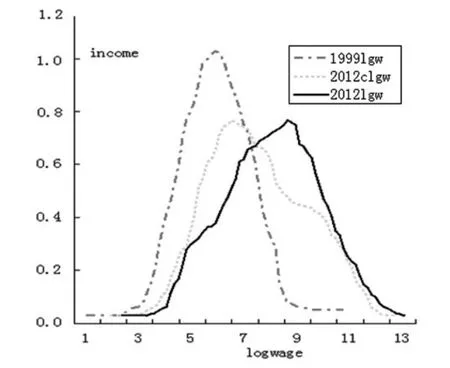
圖1 1999和2012實際收入分布和反事實收入分布對比
從圖1可以發現,2012年的反事實收入分布與2012年實際分布極其接近,這說明從1999~2012年雖然勞動者所在勞動力市場的特點(如勞動者平均受教育水平等比例提高)的確變化明顯,但是從分布圖來看,以上變化對收入分布變化的影響不很顯著。同時,2012年的反事實收入分布與1999年實際分布則差異明顯,則表明從1999~2012年收入差距的變化應該歸結為收入結構效應或別的不可觀測因素,而非由于收入組成效應。實際上,上述結論也可以通過RIF回歸分解結果來得到,在表1中收入差距衡量指標基尼系數的分解來看,1999年和2012年收入結構效應為0.231和0.294,均高于相應年份的收入組成效應0.231和0.207。
通過反事實收入分布和實際分布的比較,得出“收入結構效應”是導致1999~2012年間收入差距擴大的主要原因的結論后,我們有必要進一步分析,探究在影響收入結構效應的因素中,各個影響因素對工資結構效應的貢獻值,究竟是教育回報率的提高,還是不同職業和行業回報率的擴大。在計算時,我們使用STATA軟件計算三種衡量收入差距的指標,包括基尼系數、10~50%和10~90%,分別顯示的是總體收入差距以及收入分布上半部分高收入群體里和下半部分低收入群體里的收入差距。如10~90%就是處在收入分布90分位與處在10分位上的人收入的比例。表1即為RIF回歸分解的結果。
在1999年間,首先是年齡,其次是受教育程度和所在行業對收入結構效應的貢獻度最大,這說明年齡回報率,教育回報率和所在行業的收入回報率的變化是引起收入差距擴大的主要原因,此外從占收入分布的比例來看以上因素對低收入群體里影響更大,這意味著它們主要是通過導致低收入群體的收入差距擴大造成整個社會總體差距擴大。此外,通過1999年和2012年的對比可以發現,1999年收入結構效應在收入差距成因分解中具有優勢地位,年齡,教育程度和行業因素貢獻度最大;2012年收入組成效應則處于主導地位,這意味著此時勞動者整體平均教育水平比例提高造成的變化在收入差距成因分解中具有優勢地位。這些表明在改革開放以來,產業層次的升級導致收入差距擴大的原因逐漸變化,高的收入依賴高的教育程度和技能,而非年齡和性別等低層次的個體因素,這也為我們有針對性的扶貧措施提供了政策建議。
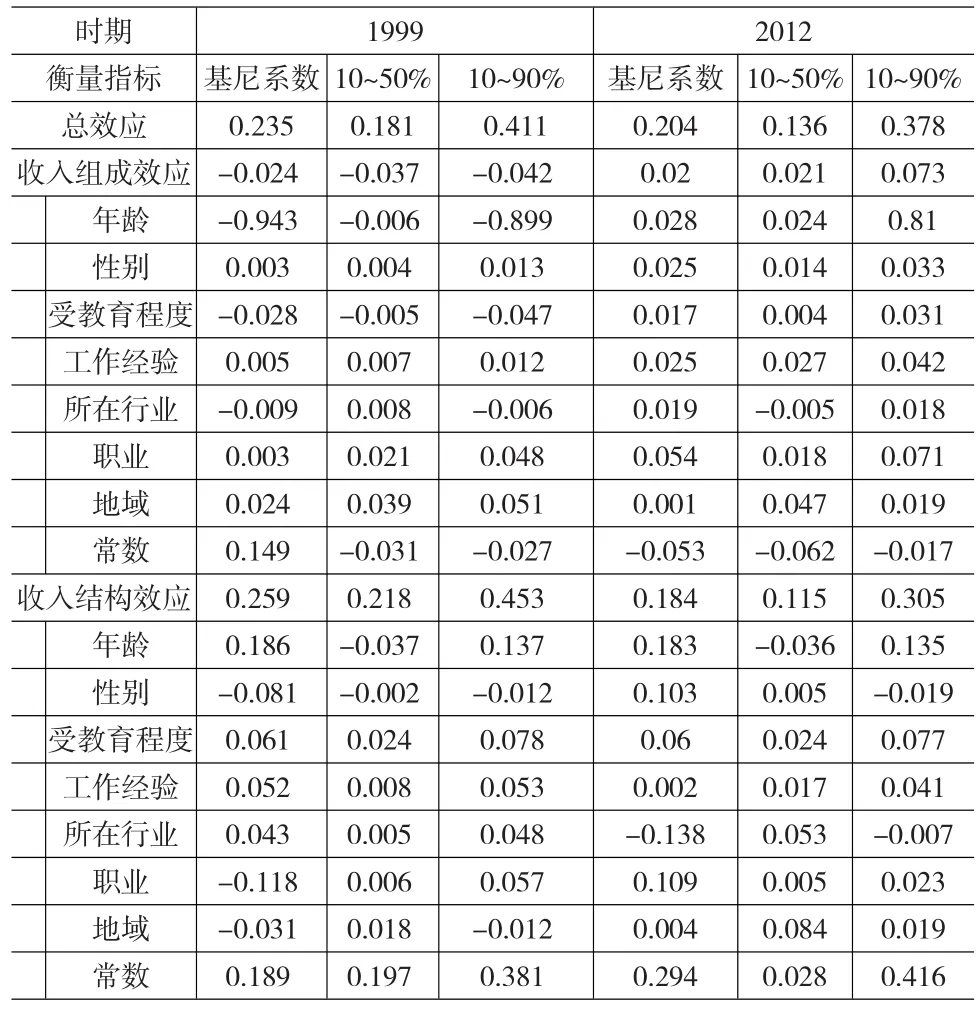
表1 1999和2012年收入差距分解和貢獻度表(%)
3 結論
本文對收入差距測度和分解的傳統方法提出商榷,提出能夠準確分解收入分布差異并具體測度其影響因素變化對收入差距貢獻度的新方法。利用“反事實分析方法”和半參統計方法構造并估計整個分布函數的“反事實”收入分布,通過RIF函數將收入分布的差異分解為收入組成效應和結構效應,得到各解釋變量變化對于整體收入分布變動的貢獻度。本文采用該方法估計了1999年和2012年我國城鎮居民的收入分布,并對收入分布變遷的成因做出分解,發現收入結構效應是導致收入差距擴大的主要原因。
[1]Firpo S,Fortin N,Lemieux T.Decomposing Wage Distribution Using Recentered Influence Function Regression[J].Econometrics,2007,(6).
[2]Powell D.Unconditional Quantile Regression For Exogenous or Endogenous Treatment Variables[J].Econometrics,2010,(2).
[3]黎波,遲巍,余秋梅.一種新的收入差距研究的計量方法—基于分布函數的半參數化估計[J].數量經濟技術經濟研究,2007,(8).
[4]朱平芳,張征宇.無條件分位數回歸:文獻綜述與應用實例[J].統計研究,2012,(3).

