時域聚總、脈沖響應與中國經濟波動的持久性特征研究

葉 光

（河南財經政法大學 經濟學院，鄭州 450046）

0 引言

宏觀經濟波動通常可視為經濟系統受外生沖擊影響后，實際產出對其潛在水平的短期偏離。對于外生沖擊的來源，經濟學界一般傾向于將其分為兩類：供給沖擊和需求沖擊，前者對產出的影響是持久的，后者的影響是暫時的。因而，考察實際產出的動態特征及其對外生沖擊反應的持久性，對于明確沖擊的主要來源，進而制定和實施有效的反周期政策具有重要意義。但利用時間序列模型對此進行研究時，經常會面臨不同頻率樣本數據的選擇問題，按觀測頻率的不同，常用的樣本數據有三類：月度、季度和年度數據，理論模型中任意相鄰兩期之間都是間隔一期，但這一期到底有多久卻無從知曉，實際應用中研究者只能從時間跨度、樣本容量和相關變量的數據可得性等方面來說明樣本選擇的合理性。樣本觀測頻率的變化會改變時間序列模型的結構設定，從而對模型分析結果產生重要影響，即便使用同樣的計量模型和分析方法，樣本觀測頻率的不同也會導致估計結果差異很大，對此如何從理論上予以解釋？不同估計結果之間存在著怎樣的聯系，如何從中探尋實際產出的真實動態特征？

時間序列從高頻到低頻的轉換即為時域聚總，對于流量數據，低頻數據為其觀測時間間隔內所有高頻數據的加總；對于存量數據，低頻數據通常由每個時間間隔內最后一個高頻觀測值構成。現有研究表明，若高頻序列的生成過程為（向量）ARIMA模型，則低頻序列的模型形式保持不變，且具有相同的單位根性質和協整關系，但模型的自回歸和移動平均結構會發生變化[1～5]這意味著利用脈沖響應函數考察經濟序列的動態特征時，使用不同頻率的樣本數據可能會得到完全不同的估計結果。Rossana和Seater（1995）分別使用美國工業生產指數、失業率和利率等變量的月度、季度和年度數據估計ARIMA模型，考察樣本觀測頻率變化對脈沖響應函數的影響，發現年度數據對應的脈沖響應函數非常平滑，而利用月度和季度數據估計的脈沖響應函數變化劇烈，形狀上也比較接近。[6]脈沖響應函數反映了變量受到外生隨機沖擊后向均衡狀態的收斂情況，對于特定的經濟變量，樣本觀測頻率的影響只能體現于不同頻率的時間序列模型中“外生沖擊”的差異，本文將從這個角度研究系統抽樣對脈沖響應函數的影響，探討不同觀測頻率下脈沖響應函數的理論聯系。

對于經濟變量對外生沖擊反應的持久性，通常用累積脈沖響應（Cumulative Impulse Response，CIR）予以度量（Andrews和Chen，1994）。[7]如果對產出的對數差分序列（增長率）構建ARMA模型，將其轉化為無窮階MA模型后，相應的移動平均系數之和與CIR完全對應，其值為0意味著產出序列為趨勢平穩過程，外生沖擊主要源于需求層面，對產出的影響是暫時的（Compbell和Mankiw，1987）。[8]劉金全等（2007）對中國實際GDP季度增長率進行分析，發現外生沖擊對中國實際產出的影響具有較強的持久性，這與孫曉濤、王少平（2012）的結論基本一致，但二者關于持久性程度的估計結果有一定區別。[9][10]樣本觀測頻率變化時，脈沖響應函數的差異本身就意味著CIR的不同，但理論上，經濟變量的持久性特征是既定的，不因數據頻率變化而改變。二者的矛盾說明，現有文獻用CIR或移動平均系數之和度量變量的持久性特征的做法是值得商榷的，在此基礎上對經濟波動持久性的研究也不夠可靠。正基于此，本文將從理論上研究時域聚總對脈沖響應函數和累積脈沖響應的影響，明確累積脈沖響應與樣本觀測頻率的關系，探尋更加穩健的關于經濟變量持久性特征的度量方法，在此基礎上分別使用月度、季度和年度數據估計國內產出對外生沖擊的動態響應路徑，為理論研究提供經驗支持的同時，更加全面地揭示中國經濟波動的持久性特征。

1 時域聚總對脈沖響應函數和累積脈沖響應的影響

1.1 對數差分序列ARMA模型的時域聚總問題

令{xt}表示高頻時間序列，每隔k期得到一個低頻觀測值，k為大于1的整數，相應的低頻序列用{XT}表示。從T-1期到T期，低頻觀測值只有一個XT，高頻觀測值則有k個：x(T-1)k+1,x(T-1)k+2,…,xTk，兩者的關系即從低頻序列到高頻序列的聚總機制，可以設定為：

其中，L 為t刻度下的滯后算子，xt-1=Lxt，XT-1=LkXT，Lk為T刻度下的滯后算子。對于存量數據，W(L)=1；對于流量數據，W(L)=1+L+…+Lk-1。在關于經濟波動持久性和其他很多實證研究中，需要使用對數差分序列（增長率）構建ARMA模型，將{xt}和{XT}的增長率序列分別表示為{yt}和{YT}，若x為存量，式（1）中聚總機制對于對數差分后的序列同樣成立，但若x為流量，需要利用式（1）重新設定yt和YT的關系。考慮到中國宏觀數據的官方發布情況和季節性因素，本文使用同比增長率進行分析。令同比增長率YT=(XT-XT-j)/XT-j，對于季度和年度序列，j分別為4和1，由式（1）可以得到：

其中，ωT為T刻度下的擾動項。若y為存量，式（5）中MA項的滯后階數為p(k-1)+q，所有大于p(k-1)+q階的自相關系數全部為零，要保證與之相同的自相關結構，式（6）中MA項的滯后階數r應該等于int[(p(k-1)+q)/k]，int為取整函數；若y為流量，r為int[((p+1)(k-1)+q)/k]（Amemiya和Wu，1972）。[1]從式（4）和式（6）中自回歸系數的關系可以看出，時域聚總不影響序列的單位根性質，且當k有限時，模型的自回歸階數也不發生變化。但對于平穩序列，|li|＜1，式（4）中高階自回歸系數非常接近于0，因而實際應用中，利用低頻序列選擇的滯后階數往往遠小于高頻序列。

1.2 時域聚總對脈沖響應函數的影響

分別利用式（5）和式（6）對YT進行預測，令高頻序列的已知信息集為Ωh={yTk-1,yTk-2,…}，低頻序列的信息集Ωl={YT-1，YT-2，…}，通過式（3）可以從 Ωh得到 Ωl，反之則不成立，這意味著高頻序列比低頻序列包含更多的數據信息。由此可以將擾動項εTK和ωT分別表示為：

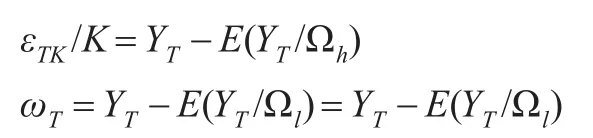
也即是說，兩個擾動項都可視為對YT的預測誤差，區別在于已知的信息集不同。進行脈沖響應分析時，高頻序列模型中外生沖擊來自于信息集Ωh之外的不可預測因素，而對于低頻序列，則是Ωl之外的不可預測因素，兩種模型中關于“外生沖擊”界定的差異必然會導致脈沖響應函數的不同。實證研究中利用不同頻率的樣本數據，通常會發現變量對單位外生沖擊有著完全不同的響應，過多關注脈沖響應函數的具體數值沒有實際意義。

利用脈沖響應函數考察外生沖擊影響的持續時間。若高頻序列模型為MA(q)過程，外生沖擊的影響持續q期，則相應的低頻序列模型中MA階數和外生沖擊影響的持續期都為int[(q-1)/k]+1，換算為高頻序列的時間單位，低頻序列模型中外生沖擊影響的持續時間大于或等于高頻序列模型，但差距在k期之內。對于一般的ARMA模型，脈沖響應函數的尾部值主要決定于AR多項式的最大根，結合式（4）和式（6）中自回歸系數的關系可以看出，當et對yt的影響衰減到接近于零時，wT對YT的影響也應該與零非常接近。

1.3 時域聚總、累積脈沖響應與持久性的度量

假定yt是協方差平穩的，系統抽樣不改變序列的平穩性，YT同樣協方差平穩，根據Wold分解定理，給出式（4）和式（6）的MA(∞ )形式：

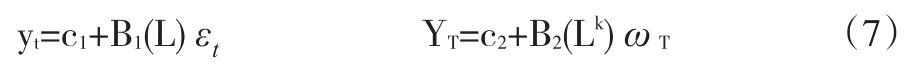
其中，c1、c2和B1(L)、B2(Lk)中諸多參數分別為式（4）和式（6）中參數的函數。從而高頻和低頻序列模型中CIR分別為B1(1)和B2(1)。利用自協方差生成函數得到：

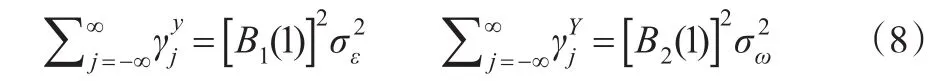
這里gjy和gjY分別表示yt和YT的j階自協方差；σε2和σω2為擾動項ε和ω的方差。

定義與yt具有相同觀測頻率的高頻序列{Yt*}，其每個觀測值皆為{yt}中前k期觀測值的樣本均值，將式（7）中yt的方程兩側同乘以W(L)/k，同樣利用自協方差生成函數得到：

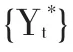
考慮到YT可近似表示為yt中前k期值的算術平均，利用不同頻率的樣本數據估計CIR時，為對估計結果進行比較，建議將高頻序列的CIR除以k。但由于式（4）和式（6）中單位沖擊的含義不同，這種做法也只能部分消除時域聚總的影響。由此可見，在使用調整后的CIR對持久性予以度量的基礎上，進一步通過脈沖響應函數考察經濟變量受到外生沖擊后向其均值的收斂時間，在此基礎上研究其持久性特征理論上更為可取。

2 樣本觀測頻率與中國經濟波動的持久性

2.1 數據來源與統計特征

為更好地說明時域聚總的影響，本文選取月度數據可獲取的工業增加值數據來研究產出波動的動態特征。工業增加值實際同比增長率直接源于國家統計局公布的“規模以上工業企業增加值當月同比實際增速”，時間跨度是1990年10月到2014年12月。由于其1、2月份數據受春節因素影響很大，國家統計局不發布1月當月數據，自2013年起，2月份當月數據也不再發布，本文以1-2月份累計同比增速作為2月份當月數據，1月份數據由插值估算。圖1給出了三種觀測頻率下中國工業增加值同比增速的變化特征，三者具有非常類似的長期趨勢，但從短期變化來看，觀測頻率越高的序列短期變化越劇烈。

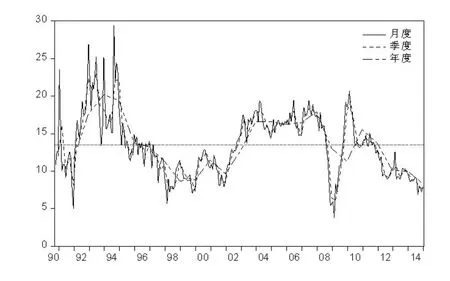
圖1 不同頻率下中國工業增加值同比增速的變化特征

從圖1可以看出，從上世紀90年代初期的高通脹階段之后，到2008年全球金融危機爆發之前，中國經濟先后經歷了持續時間很長的低速調整時期和高速增長時期。前者從1996年開始到2002年結束，共持續了8年，主要歸因于國內長期實施的經濟“軟著陸”政策和1998年亞洲金融危機的影響。2003年之后，在出口拉動和“雙穩健”政策的共同作用下，中國經濟開始了持續5年的高速增長時期。2007年下半年國內經濟開始面臨較大的通脹壓力，特別是房地產價格的居高不下，迫使政府出臺了一系列的調控措施，但并沒有取得理想的實際效果。直到2008年在美國金融危機和“從緊”貨幣政策的雙重壓力下，經濟增速出現了近20年來最嚴重的下滑，中國經濟開始由高速增長轉向低速調整的“新常態”階段。總體來看，中國的經濟波動表現出了比較明顯的強持久性，供給層面的沖擊可能是國內經濟波動的主要來源，在供給層面整體不夠健全的情況下，4萬億投資計劃僅帶來了2009年曇花一現的恢復，單靠需求管理政策已經很難保證中國經濟的平穩快速發展。因而，新一屆政府開始將政策著力點由需求管理轉向供給管理，注重經濟結構調整和企業自主創新能力的培養。

表1 中國工業增加值同比增長率序列的ADF單位根檢驗

對工業增加值同比增長率序列進行ADF單位根檢驗，結果如表1所示。樣本觀測頻率的變化不改變序列的單位根性質，表中基于月度和季度數據的檢驗結果完全一致，即在5%顯著水平下拒絕存在單位根的零假設，1990年以來中國工業增加值的同比增長率序列是平穩的。我們也對年度序列進行了單位根檢驗，利用AIC準則選擇的滯后階數為3，ADF統計量值為-2.83，p值為0.07，但由于年度數據的樣本容量僅為24，這種情況下單位根檢驗的功效很低，實際檢驗水平的扭曲也比較嚴重。如果適當提高檢驗水平，在10%水平下依然可以認為序列是平穩的。因此，本文將直接對工業增加值同比增長率序列構建ARMA模型，在此基礎上研究中國經濟波動的持久性特征。

2.2 中國經濟波動的動態特征

2.2.1 經濟波動的持久性

假定工業增加值同比增長率序列的真實過程為ARMA模型，時域聚總不改變模型形式，對于月度、季度和年度序列，都可以使用ARMA模型進行擬合。但當樣本觀測頻率發生變化時，模型的自回歸階數p和移動平均階數q會隨之改變，在確定滯后階數時，主要關注序列相關檢驗的Q統計量值，以保證擾動項的白噪聲性。如果滿足條件的滯后階數不唯一，選擇AIC準則取值最小者。對于模型中可能存在的不顯著項，若將其刪除會導致序列相關，則予以保留。表2給出了與三種頻率樣本數據相對應的模型滯后階數、估計結果和相關統計量的值，從Q統計量的表現來看，表中滯后階數的設定足以消除模型的序列相關性。

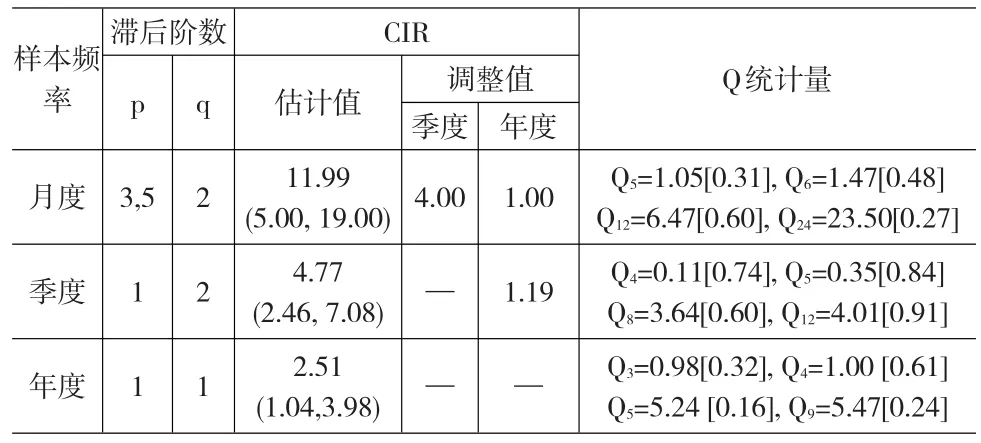
表2 不同樣本觀測頻率下中國經濟波動持久性的估計值（1990-2014）

由于不同頻率的ARMA模型中擾動項的方差不同，為便于比較，我們通過考察單位沖擊的影響來計算累積脈沖響應（CIR）。從表2可以看出，CIR的估計值與數據頻率密切相關，數據頻率越高，估計結果越大，與前文理論分析的結論保持一致。使用月度數據估計的CIR最大，為11.99，但隨著觀測頻率的降低，其數值不斷減小，季度數據的估計值減小到4.77，年度數據進一步下降到2.51。這一方面說明無論使用何種頻率的樣本數據，都能發現中國的經濟波動具有較強的持久性，另一方面則意味著，忽略樣本觀測頻率的差異，僅關注CIR所反映的持久性程度，很難真正揭示經濟波動的動態特征。

將月度序列聚總為季度序列時，式（3）中k等于3，為此我們以月度CIR除以3作為調整到季度水平的CIR，調整后的估計值為4.00，與直接使用季度模型得到的估計值非常接近。對于年度水平的CIR，利用月度或季度模型得到的調整值比較接近，但都明顯低于基于年度模型的估計結果，其原因有兩點：一是與月度或季度序列相比，年度序列損失了大量的數據信息，從而脈沖響應分析中單位沖擊的含義明顯不同；二是年度數據的樣本容量較小，模型估計結果可能存在較大誤差。但總體來看，調整后的估計值受樣本觀測頻率的影響明顯減弱，對不同觀測頻率下CIR的估計結果進行比較時，調整后的結果更具有可比性。此外，雖然表2中調整后的估計結果比較接近，一定程度上揭示了中國經濟波動的持久性特征，但這也只能告訴我們外生沖擊的影響會持續一段時間，但具體有多久，還需要借助脈沖響應函數進一步研究。

2.2.2 脈沖響應函數

圖2描繪了利用月度、季度和年度數據估計的脈沖響應函數，橫軸刻度為月份。除初始階段略有差異之外，月度和季度數據對應的脈沖響應函數比較接近，半衰期分別為7個月和9個月，第3年末大致收斂到均衡狀態。利用年度數據估計的脈沖響應函數數值上明顯大于月度和季度數據的估計結果，半衰期接近2年，但同樣在第3年末收斂到均衡狀態。如果僅僅關注外生沖擊的持續時間，從圖2可以看出，使用不同頻率的樣本數據所得到的結論基本一致，這與前文的理論分析非常吻合。相對而言，年度脈沖響應函數的時間跨度過大，很難真正表現出經濟變量對外生沖擊的短期動態反應，當我們主要關注這種動態響應路徑時，利用月度數據或季度數據進行脈沖響應分析顯然更為可取。

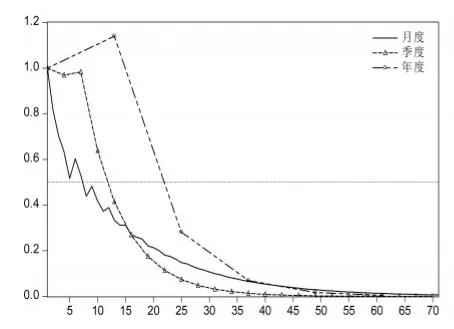
圖2 不同樣本觀測頻率下的脈沖響應圖

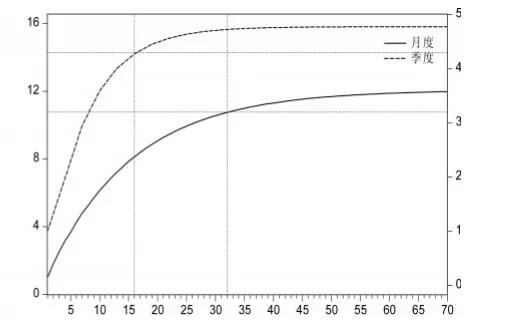
圖3 月度與季度累積脈沖響應圖

由于脈沖響應函數通常呈指數衰減，很難精確判斷具體的收斂時間，從可操作性角度看，人們可能更關心外生沖擊的影響絕大部分在多長時間內實現。圖3描繪了中國工業增加值同比增速的月度和季度累積脈沖響應圖，分別對應著左側和右側縱軸，橫軸刻度為月份。雖然二者脈沖響應函數比較接近，但累計脈沖響應函數存在比較明顯的差異。圖中二者實現最終收斂值的90%部分所需要的時間分別為16個月和32個月，相差整整1倍。對于年度脈沖響應函數，實現90%影響的時間在2年和3年之間。在缺乏進一步信息來判斷哪個結論更為準確的情況下，只能得到一個比較寬泛的區間，即外生沖擊對中國實際產出的影響大致需要經過1年半到3年的時間才能完全實現。

外生沖擊對中國經濟的影響大致會持續3年左右，半衰期接近2年，說明中國的經濟波動具有較強的持久性。這種持久性一定程度上源于長期實施的“軟著陸”和“軟擴張”調控政策，但不能因此忽略中國經濟自我調整和穩定機制的欠缺。因而，“新常態”下政府不僅要著力調整經濟結構和轉變經濟增長方式，還要切實減少對市場主體微觀經濟行為的過度干預，不斷完善市場體系，真正發揮市場在資源配置中的作用，逐步提高經濟的自我調節能力。

3 結論

本文針對常用的ARMA模型，從理論上探討時域聚總對脈沖響應函數和累積脈沖響應的影響，在此基礎上全面考察中國經濟波動的持久性特征。主要結論如下：

累積脈沖響應通常會隨著樣本觀測頻率的提高而增加，直接用其度量變量的持久性特征并不可取。研究經濟波動的持久性特征時，為保證不同頻率樣本數據的估計結果具有可比性，建議將利用高頻序列估計的累積脈沖響應除以k。系統抽樣對脈沖響應函數的影響主要在于“外生沖擊”界定的不同，實證研究中過多關注脈沖響應函數的具體數值意義不大，但可以通過脈沖響應函數考察外生沖擊影響的持續時間，其反應的持久性特征理論上更為可信。

關于經濟波動持久性的研究表明，外生沖擊對中國經濟的影響大致會持續3年左右，半衰期接近2年，中國的經濟波動具有較強的持久性，供給層面的沖擊是國內經濟波動的重要原因。政府在將政策著力點由需求管理轉向供給管理的同時，還要切實減少對市場主體微觀經濟行為的過度干預，不斷完善市場體系，真正發揮市場在資源配置中的作用，逐步提高經濟的自我調節能力。

[1]Amemiya T，Wu RY．The Effect of Aggregation on Prediction in The Autoregressive Model[J].Journal of The American Statistical Association，1972,（339）．

[2]Brewer K R W．Some Consequences of Temporal Aggregation and Systematic Sampling for ARMA and ARMAX models[J]．Journal of Econometrics，1973,（1）．

[3]Weiss A A．Systematic Sampling and Temporal Aggregation in Time Series Models[J].Journal of Econometrics，1984（3）．

[4]Granger C W J，Siklos P R．Systematic Sampling,Temporal Aggregation,Seasonal Adjustment,and Cointegration[J].Journal of Econometrics，1995（1）．

[5]Marcellino M．Some Consequences of Temporal Aggregation in Empirical Analysis[J].Journal of Business&Economic Statistics，1999（1）．

[6]Rossana R J，Seater J J．Temporal Aggregation and Economic Time Series[J].Journal of Business&Economic Statistical，1995（4）．

[7]Andrews D W K，Chen H Y．Approximately Median-Unbiased Estimation of Autoregressive Models[J].Journal of Business&Economic Statistical，1994（2）．

[8]Campbel J，Mankiw G． Permanent and Transitory Components in Macroeconomics Fluctuations[J].The American Economic Review，1987（2）．

[9]劉金全,劉志剛,李慶華.我國實際產出序列的周期成分分解與周期波動的持久性度量.中國數量經濟學會.21世紀數量經濟學[C].北京：社會科學文獻出版社，2008．

[10]孫曉濤，王少平.我國的經濟波動來自供給沖擊還是需求沖擊?——對我國GDP波動持久性的度量.中國數量經濟學會.21世紀數量經濟學[C].北京：社會科學文獻出版社，2013．