基于MSC.Nastran的某校車車身結構的模態分析

王若平， 劉圣仲

(江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013)

?

基于MSC.Nastran的某校車車身結構的模態分析

王若平， 劉圣仲

(江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013)

應用有限元前后處理軟件Patran對車身骨架進行有限元建模，然后導入MSC.Nastran進行無阻尼自由振動狀態下的模態研究，得到該校車車身骨架結構有限元模型的模態,并對得到的理論模態參數進行分析，為該車車身骨架的設計方案提供全面的評價。

校車；車身骨架；模態分析；MSC.Nastran

2012年4月，國家質量監督檢驗檢疫總局、國家標準化管理委員會制定了《專用校車安全技術條件》(GB24407—2012)和《專用校車學生座椅系統及其車輛固定件的強度》(GB24402—2012)兩項強制性國家標準。這兩項標準對校車安全性能的要求有了很大提升，特別是對車身結構強度的要求。

作為校車車身最為重要的參數之一,模態參數數據可以采用計算和模態參數識別試驗兩種方法來獲取。但是對于體積龐大、結構復雜的校車車身骨架,采用試驗方法進行模態分析具有周期長、成本高等局限，而且產品進行優化設計后還需重新進行試驗，因此目前普遍使用計算的方法進行模態分析。模態分析是動態分析的基礎和重要內容。在行駛過程中,校車車身結構在各種振動源的激勵下會產生振動,如發動機運轉、高速行駛時的風力，以及路面不平引起的振動等。這些振源的激勵頻率如果接近于車身整體或局部的固有頻率就會產生共振,出現劇烈振動和噪聲,甚至造成結構破壞[1]。為提高汽車的安全性、可靠性和舒適性，必須對車身結構的固有頻率進行分析,通過對結構的優化設計來避開各種振源的激勵頻率。據有關研究表明：車身的動剛度在最近幾十年來得到了很大提高，而車身的質量卻呈現一定程度的下降，這正是得益于有限元法和模態分析在汽車設計中的成功應用[2-15]。本文采用有限元軟件MSC.Nastran對某校車進行模態分析,并對其動態性能進行評價。

1 車身骨架有限元模型的建立

1.1 車身骨架幾何模型的建立

利用Pro/E Wildfire5.0 軟件[7]建立車身骨架的三維實體模型。實體模型建立之后，將其導入到Hypermesh[8]，通過軟件的提取中面功能得到車身骨架的中面模型，然后經過幾何清理得到車身骨架的最終三維實體模型，如圖1所示。

1.2 單元的選取

通過有限元分析軟件NASTRAN建立車架的三維有限元模型。由于校車車身骨架結構復雜、計算量大，因此選用三維板殼單元(SHELL)模擬車架，用梁單元(BEAM)模擬車身骨架前后側圍。

1.3 網格劃分

采用混合網格劃分的方式劃分網格。車架結構部分采用四邊形單元劃分，以獲得好的網格質量，減少單元數目；對于幾何形狀復雜的區域，充分利用三角形單元適應性強的優點，采用三角形網格。考慮到計算精度和準確性，網格單元尺寸選擇30～50 mm，本次建模把單元尺寸設置為50 mm。劃分好后的模型有5 015個節點。建立的有限元模型如圖2所示。

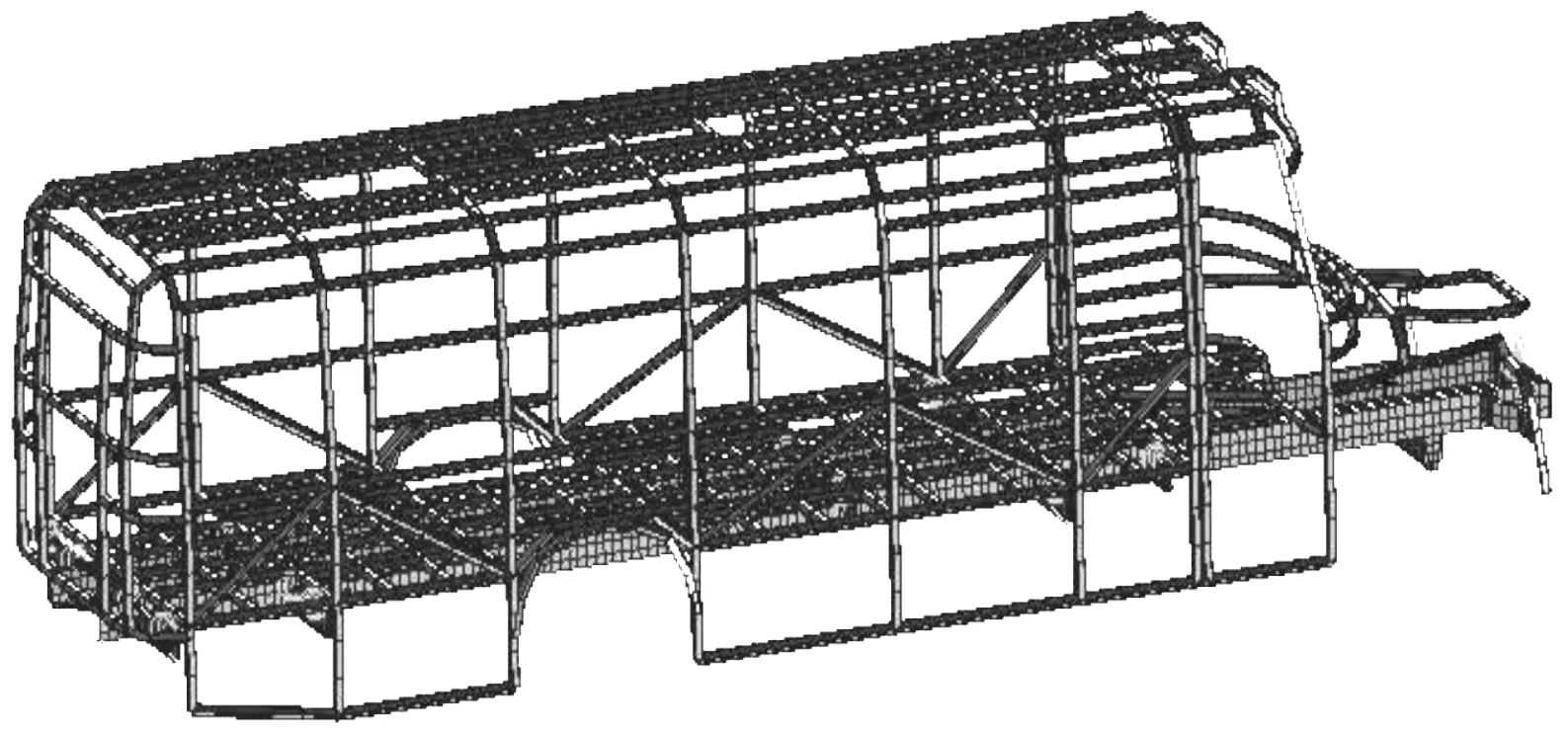
圖2 車身骨架有限元模型

1.4 材料模型的建立

在有限元前處理過程中進行單元材料屬性賦值時，所選材料的類型特征應與實際情況相符。本文研究的校車車身骨架使用KQJ和KQF系列冷彎型鋼，這種材料可看作是各向同性材料，其力學性能見表1[9]。

校車車架橫梁、縱梁等使用的材料為Q345系列鋼型，其力學性能見表2。

表1 車身骨架材料的力學性能

表2 校車車架橫梁、縱梁等使用的材料的力學性能

2 模態分析的理論基礎

由振動理論可知，在初始激勵作用下，無阻尼單自由度系統將以自身的固有頻率在某一種自然狀態下進行自由振動。而多自由度系統的自然狀態是指整個系統在運動過程中所存在的某一位移形狀。多自由度系統在振動過程的位移形狀具有多樣性，其種類數量與整個系統的自由度數量一致，這些位移的形狀即為系統的固有振型。當系統受到來自于外界的激勵時，將按照其中一種固有振型進行簡諧振動。在振動過程中，系統各個質點具有同步性，并且相互之間的位移比例保持不變。每一階振型都對應一個固定頻率，因此可以用振型和固有頻率來表示系統的振動特性，所以模態分析又稱無阻尼自由振動系統的特性分析[12-13]。

有限元分析求解中有很多常用、高效的算法,例如NewMark方法、直接疊加法和子空間迭代法等。對于具有有限個自由度的線彈性系統，根據達朗貝爾原理,可以推得動力平衡方程為[6]

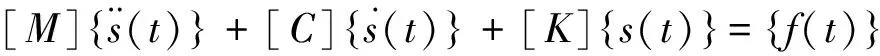
(1)

式中： [M] 為系統的質量矩陣； [K] 為系統的剛度矩陣； [C] 為系統的阻尼矩陣；f(t) 為系統的激勵力向量；s(t) 為系統的位移響應向量。

如果阻尼矩陣 [C] 滿足Fawzy條件，即 [K][M][C] = [C][M]-1[K],則振動系統為黏性比例阻尼系統，也稱為比例阻尼系統。當此系統擁有有限個自由度時，其振動方程可用式(1)來表示。式(1)是由系統的物理坐標所描述的耦合方程組，將式(1)進行傅里葉變換可得到新的微分方程：

(2)

則可求得系統第i點的響應為

(3)

式中：φij為第i測點第j階模態振型的系數；qj(η) 為第j階模態坐標。

將 {φ}j記為系統的第j階模態向量，它由系統中n個點的振型系數所組成的列向量組成，其中：

(4)

模態矩陣 [φ] 由系統各階模態向量組成，其中：

(5)

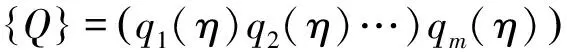
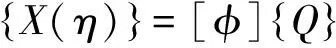
(6)

將式(2)代入式(6)有

(7)

若系統為無阻尼自由振動系統，則式(7)可改寫為

(8)

式 (8)有解的條件為

(9)

由式 (9)可求得系統的固有振動頻率為fi=ηi/2π。將fi代入式 (7)即可求得系統的固有振型 {φ}i。通常用子空間迭代法求解式 (9)中的特征值。為了求得正則坐標下的主振型，還需將固有振型 {φ}i正則化處理。

3 車身骨架自由模態分析和優化建議

3.1 基于MSC.Nastran的自由模態分析

校車車身的模態分析主要是求解車身結構的固有頻率和固有振型，可在車身骨架無阻尼的自由振動狀態下求解。求解時既不考慮車身剛度和慣性與變速箱、發動機等部件的相互耦合作用，也不考慮乘員及車載行李的質量，只考慮車身骨架的質量。 但是對于這種結構復雜、多自由度的大型車架系統,想要一一求解出其固有振型向量和所對應的固有頻率是很困難的。而在其動態響應中，系統較低的幾階振型向量和固有頻率就能直觀地反映其振動特性,故在研究系統的動態響應時,只需要求解前幾階的固有頻率和振型向量。因此，要對車身骨架的計算模態進行反復甄別，找出最能反映車身整體振動的幾階模態[10]。本文在MSC.Nastran軟件中選用蘭索斯(Lanczos)方法作為特征值求解法，提取校車車身骨架的前10階模態振型，如表3所示。第1～3階模態見圖3～5。

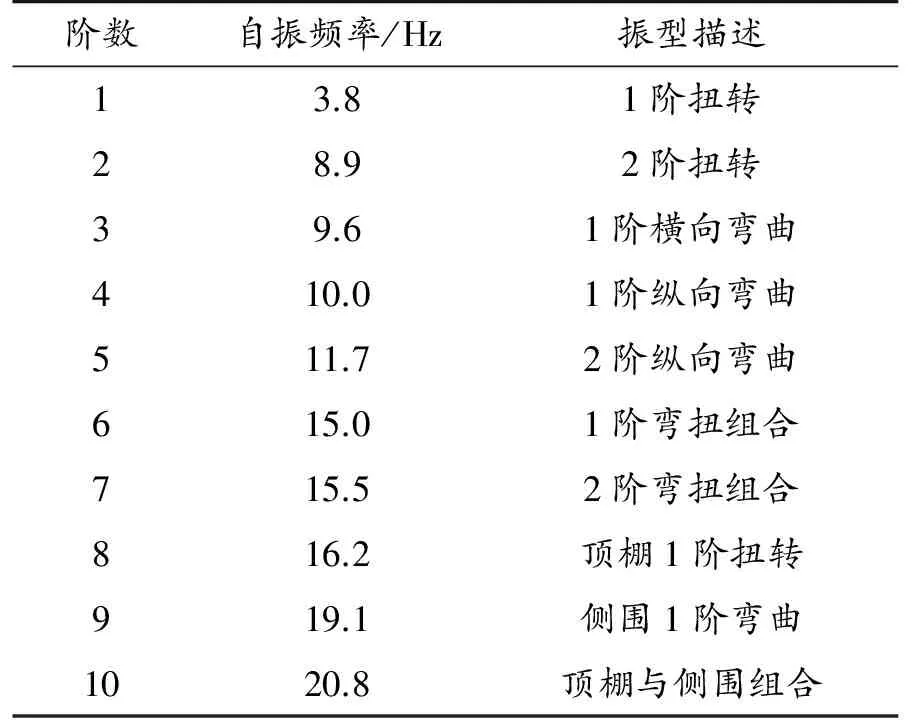
表3 校車車身骨架的前10階模態振型

3.2 模態分析結果分析

由模態分析結果可知，校車的前10階固有頻率值為3.5～15.5 Hz。在校車正常行駛過程中，車身受到的主要激勵源有車輪不平衡引起的轉動、發動機運轉、傳動軸的不平衡以及路面不平等[12]。就目前國內高速公路和城市柏油路面而言，車速在100 km/h時，激振頻率小于3 Hz，激勵分量較大。車輪不平衡產生的激振頻率一般小于11 Hz，考慮到現代輪輞制造工藝水平較高，此激勵分量可以忽略不計。校車在城市中車速往往為40～80 km/h，高速公路上的行駛車速為100～120 km/h，因傳動軸不平衡所產生的激振頻率一般為33～68 Hz[9]。該校車采用六缸柴油機，額定發動機怠速工況轉速為700 r/min。

(10)

式中：i為發動機汽缸數；ne為發動機轉速(r/min)。

由式(10)計算得到發動機的怠速激振頻率為35 Hz。由前面的分析可知：車身骨架的前10階理論固有頻率應該介于3～35 Hz，這樣才能保證車身骨架具有良好的振動特性。同時，1階彎曲模態頻率和1階扭轉模態頻率要相差3 Hz以上，以避免出現耦合效應。從模態分析的結果來看，校車車身前10階固有頻率為3.5～15.5 Hz，錯開了激勵分量較大的激振頻率，車身結構不會發生共振現象。由于本文建模時省去蒙皮以及一些非承載結構，所以計算出的車身骨架的理論固有頻率要低于實際值。但從總體上來說，該車車身骨架的動態性能良好，滿足結構安全要求。

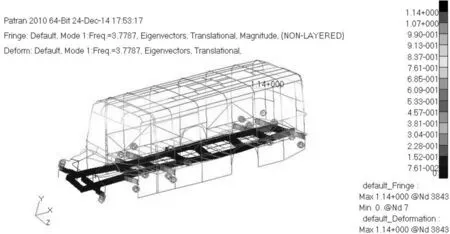
圖3 第1階模態

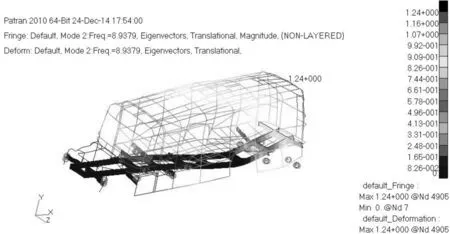
圖4 第2階模態

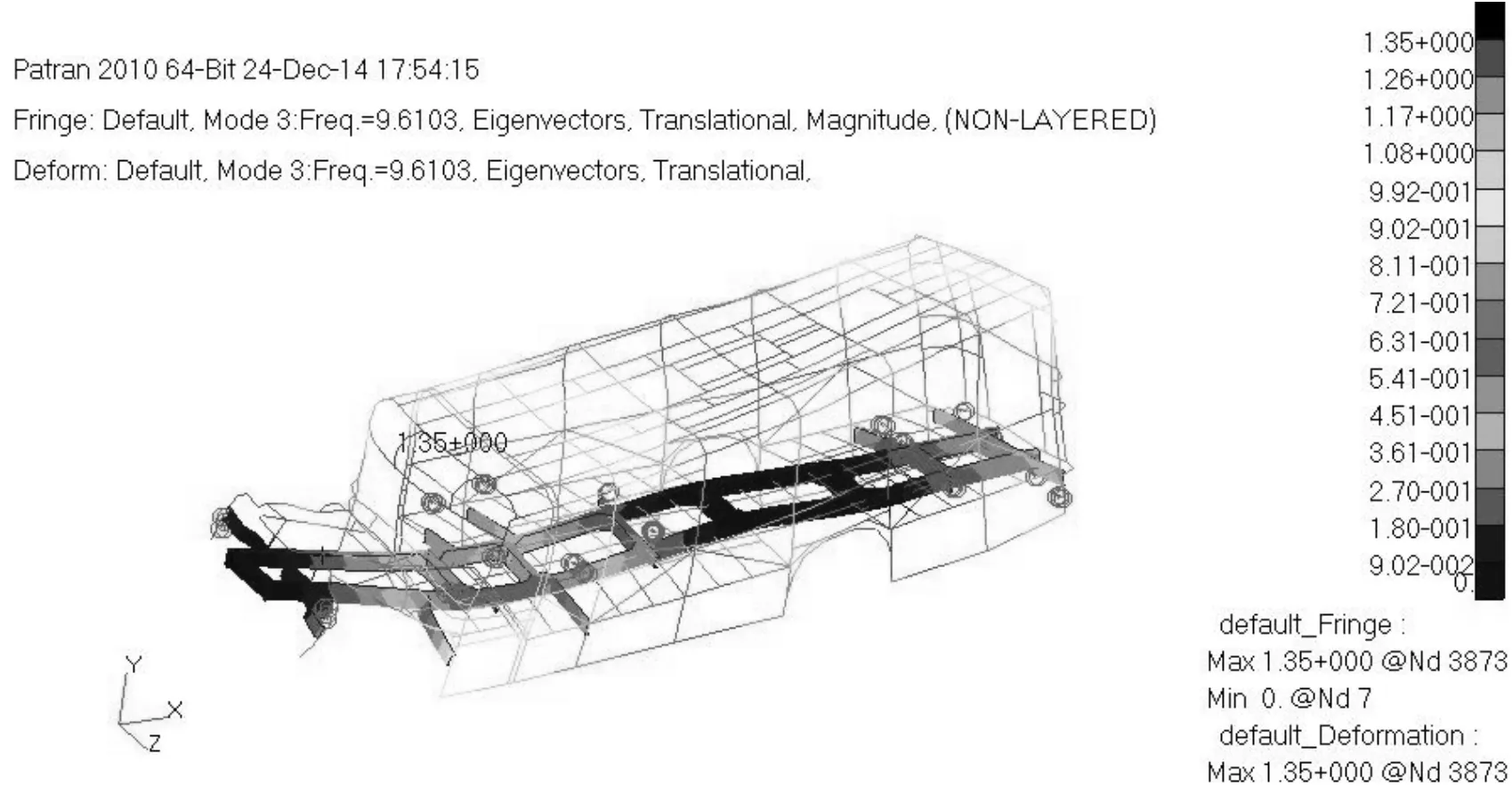
圖5 第3階模態

3.3 車身骨架振動分析和優化

在不同頻率下各部分振幅不盡相同，當某幾個節點在大多數頻率下的振幅都較大時則需對與該節點有聯系的骨架部分進行分析，在整個車身設計中全面考慮并加以改進。由各階振型圖可見，校車車身骨架整體各部位振動較為和諧。在部分頻率下，振幅大、振型多的現象大多出現在頂棚后側和后側圍艙門的上橫梁上(如圖6所示)，而此橫梁是固定后艙安全門的主要承載梁，其強度保證了艙門與后圍的配合，在此處必須找出加強骨架的方法以保證校車的安全性要求。

圖6 優化前的第4階模態

為保證順利裝配,后圍骨架縱橫梁采用規格為30 mm×30 mm×1.5 mm的矩形鋼管。由于其本身長度大，在激勵作用下振幅明顯增大，同時該部位位于車廂后側艙門上部，故該艙門出于校車安全設計的要求，必須保證一定的尺寸和強度。此外，下方的支撐剛性也比其他橫梁差。在這些方面的綜合作用下，該處的振幅較其他位置大。對于該處結構的改進，在保證客車裝配性要求的提下，可以通過增加橫梁的載面尺寸或壁厚解決。截面尺寸可更改為40 mm×40 mm×1.5 mm，或者型材壁厚可增加為2 mm，由此提高抗彎載面模量。還可通過在該橫梁與安全門兩側縱梁之間增加短橫梁以提高該處剛性和彎曲動載荷，有效減小振幅。為減少工作量和降低成本，本文采用增加短橫梁的方法。優化后再次進行模態分析得到第4階模態振型，如圖7所示，可見后圍薄弱部位振幅明顯降低，確保了骨架的承載安全。

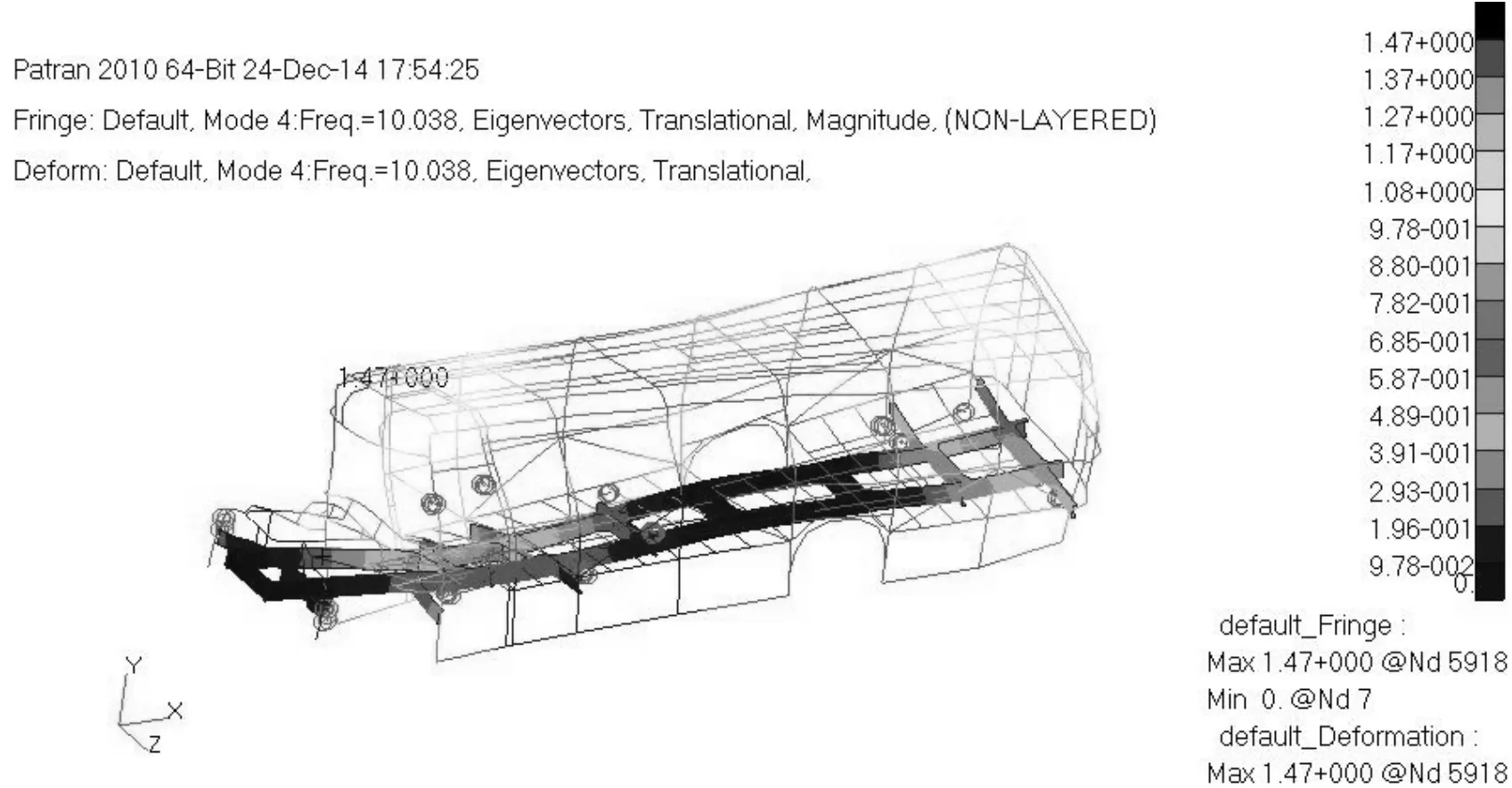
圖7 優化后的第4階模態

4 結束語

本文首先使用Proe對某品牌校車進行三維實體建模，然后利用Patran對其車身骨架進行了有限元建模，而后使用MSC.Nastran對車身骨架進行了無約束無載荷的自由模態分析。通過分析計算得到了車身骨架的固有頻率和振型。提取了前10階模態進行分析，并對該骨架的動態性能進行了評價。對薄弱區域提出相應的優化措施。模態分析結果可為車身進一步動力學分析和設計優化提供參考。

[1] 余志生.汽車理論[M].北京:機械工業出版社,2000.

[2] 季文美,方同,陳松淇.機械振動[M].北京:科學出版社,1985.

[3] 秦民， 蔣永峰， 馬天飛，等. 懸架液壓襯套液固耦合有限元分析[J]. 重慶理工大學學報:自然科學版，2014(7)：5-10.

[4] 王若平， 柳淑云， 朱國梅. 大客車車身骨架早期局部開裂分析[J]. 重慶理工大學學報:自然科學版， 2014,28(11):1-5.

[5] 傅志方.振動模態分析與參數識別[M].北京:機械工業出版社,1990.

[6] 傅志方,華宏星.模態理論分析與應用[M].上海:上海交通大學出版社,2000.

[7] 李軍.精通PRO/ENGINEER中文野火版-零件設計篇[M].北京:中國青年出版社,2004.

[8] 于開平,周傳月,譚惠豐,等.Hypermesh從入門到精通[M].北京:科學出版社,2005.

[9] 機械工程材料性能數據手冊編委會.機械工程材料性能數據手冊[M].北京:機械工業出版社,1994.

[10]張晶，張瑞乾.某微型客車車身模態分析[J].機械制造與制動化，2012,41(6):100-102.

[11]沈浩，陳昌明，雷雨成.客車車身模態分析及評價[J].公路交通科技,2003,20(2):128-130.

[12]王濤.客車車身動態特性研究[D].合肥：合肥工業大學,2011.

[13]曹樹謙，張文德，蕭龍翔.振動結構模態分析理論、分析與應用[M]. 天津：天津大學出版社，2001.

[14]張準，汪鳳權.振動分析[M].南京：東南大學出版社,1991.

[15]Beermann H J. Static analysis of commercial vehicle frames:a hybrid finite element and analytical method [J].Int.J.of Vehicle Design， 1984,5(1):25-26.

(責任編輯 劉 舸)

Modal Analysis of a Bus Body Structure Based on MSC.Nastran

WANG Ruo-ping, LIU Sheng-zhong

(School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

The finite element modeling for auto- body structure was carried out with the help of pre and post processing software for finite element-Patran. The solution of modal analysis to the model in undamped free vibration was performed with MSC.Nastran and the post processing analysis of the calculated result was carried out with Hypermesh. Based on the finite element analysis of school bus’ body structure, a comprehensive evaluation and improvement for the design of the car body frame was provided.

school bus; auto-body; model analysis; MSC.Nastran

2014-12-06 作者簡介：王若平(1960—)，女，黑龍江哈爾濱人，博士，教授，主要從事汽車理論設計與方法研究；通訊作者 劉圣仲(1990—)，男，江蘇人，碩士研究生，主要從事車輛安全研究。

王若平，劉圣仲.基于MSC.Nastran的某校車車身結構的模態分析[J].重慶理工大學學報：自然科學版，2015(3):5-9.

format：WANG Ruo-ping，LIU Sheng-zhong.Modal Analysis of a Bus Body Structure Based on MSC.Nastran[J].Journal of Chongqing University of Technology:Natural Science,2015(3):5-9.

10.3969/j.issn.1674-8425(z).2015.03.002

U463

A

1674-8425(2015)03-0005-05