具有分布時滯脈沖Cohen-Grossberg神經網絡的穩定性分析

張 韜，蘇亞坤，朱 進

(渤海大學 數理學院，遼寧錦州 121000)

Cohen-Grossberg神經網絡是由Cohen和Crossberg于1983年提出的［1］，被廣泛地應用于模式識別、記憶與信號處理、圖象處理與計算技術等領域。然而，在實際應用中時滯、脈沖是不可避免的，且時滯、脈沖對神經網絡的穩定性有著巨大的影響［2-8］，因此有關時滯脈沖Cohen-Crossberg神經網絡的研究［9-19］已逐漸引起人們的關注，研究脈沖型時滯神經網絡具有極其重要的意義。

1 問題描述及相關假設

神經網絡模型如下:

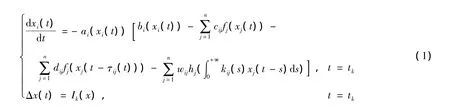
初始條件x(t0+s)=φ(s)，0≤τij(t)＜τij(t)≤η＜1，其中:x(t)=(x1(t)，x2(t)，…，xn(t))表示神經元狀態向量;ai(·)表示放大函數;bi(·)表示適當的行為函數;fj，hj為神經元的激勵函數;C=(cij)n×n，D=(dij)n×n，W=(wij)n×n分別表示連接權矩陣、時滯連接權矩陣和分布時滯連接權矩陣。固定時刻tk滿足t1＜t2＜t3＜…，且在 tk時刻，Δ x(t )Rn」表示在tk時刻的狀態變化，對所有的k∈N，Ik(0)=0。

要求神經網絡模型滿足以下假設:

1)存在正常數 Lj，Hj，j=1，2，…，n 使得

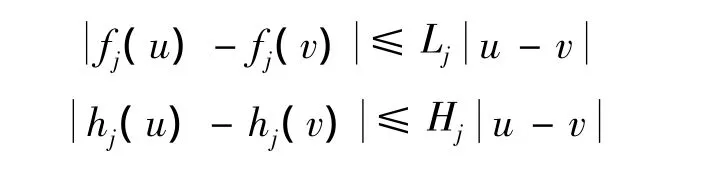
4)?σk≥0，k∈N，有

5)?μ ＞1，有 μτ≤inf{tk-tk-1};

6)max{ θk}≤M ＜ e2λμτ，M 是常數，θk=1+(2σk+);

7)延遲核函數 Kij，i，j=1，2…n是定義在［0，∞)上的實值非負函數，滿足，其中λ是正常數。

2 主要結果

定理 在假設1)～7)下，如果?λ＞0，正對角矩陣Q=diag(q1，…，qn)，使得

其中

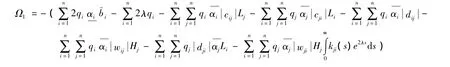
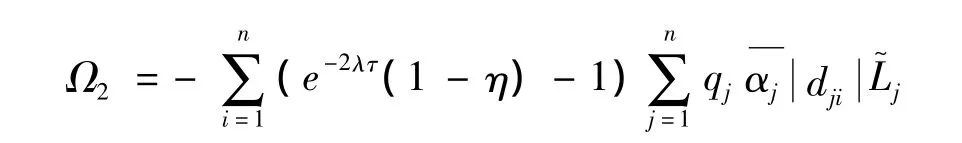
那么模型(1)的零解是全局指數穩定的。

證明 構造如下Lyapunov-Krasovskii泛函:

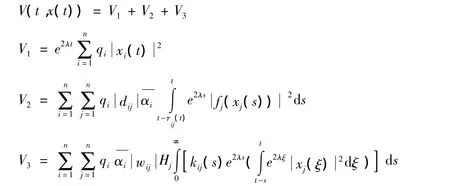
當 t≠tk時

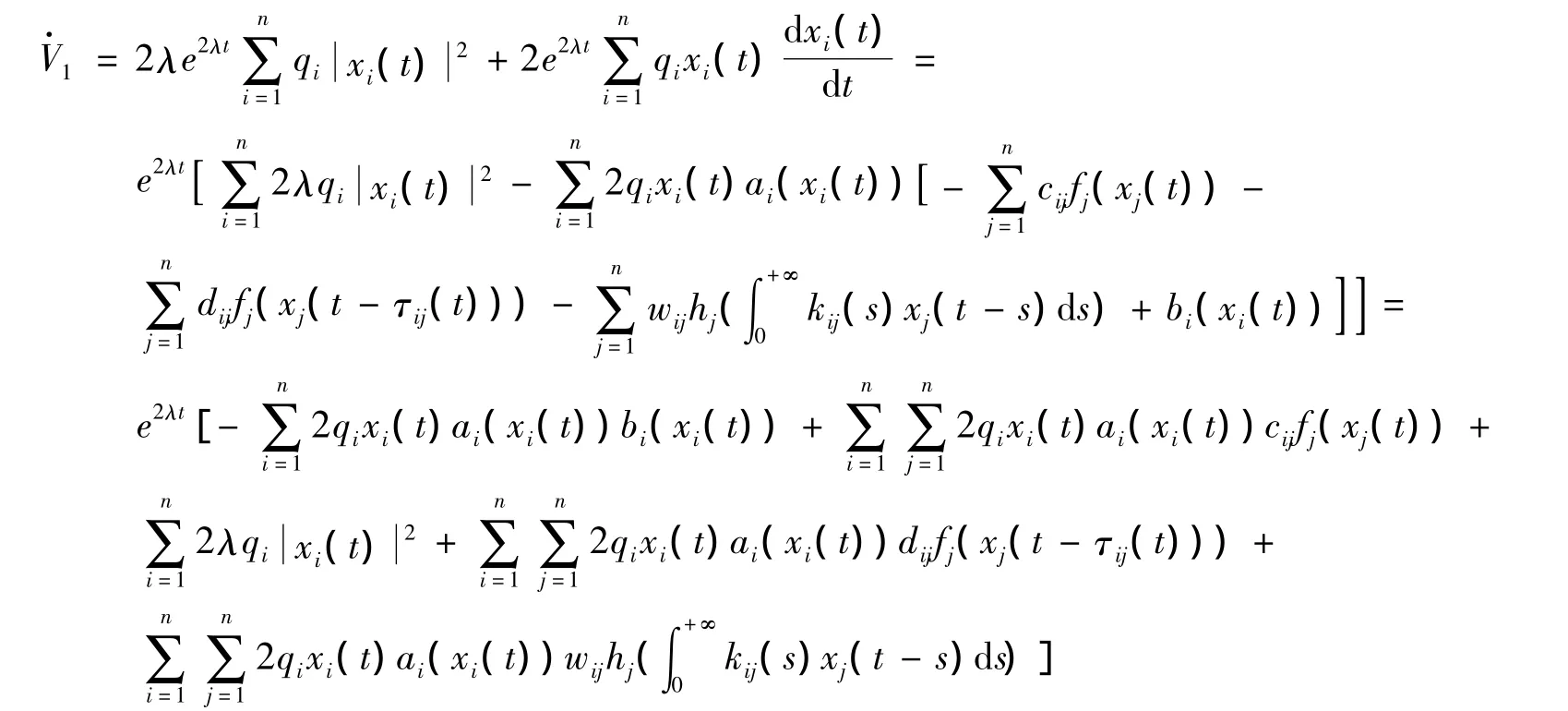
利用條件1)～3)和2ab≤a2+b2得

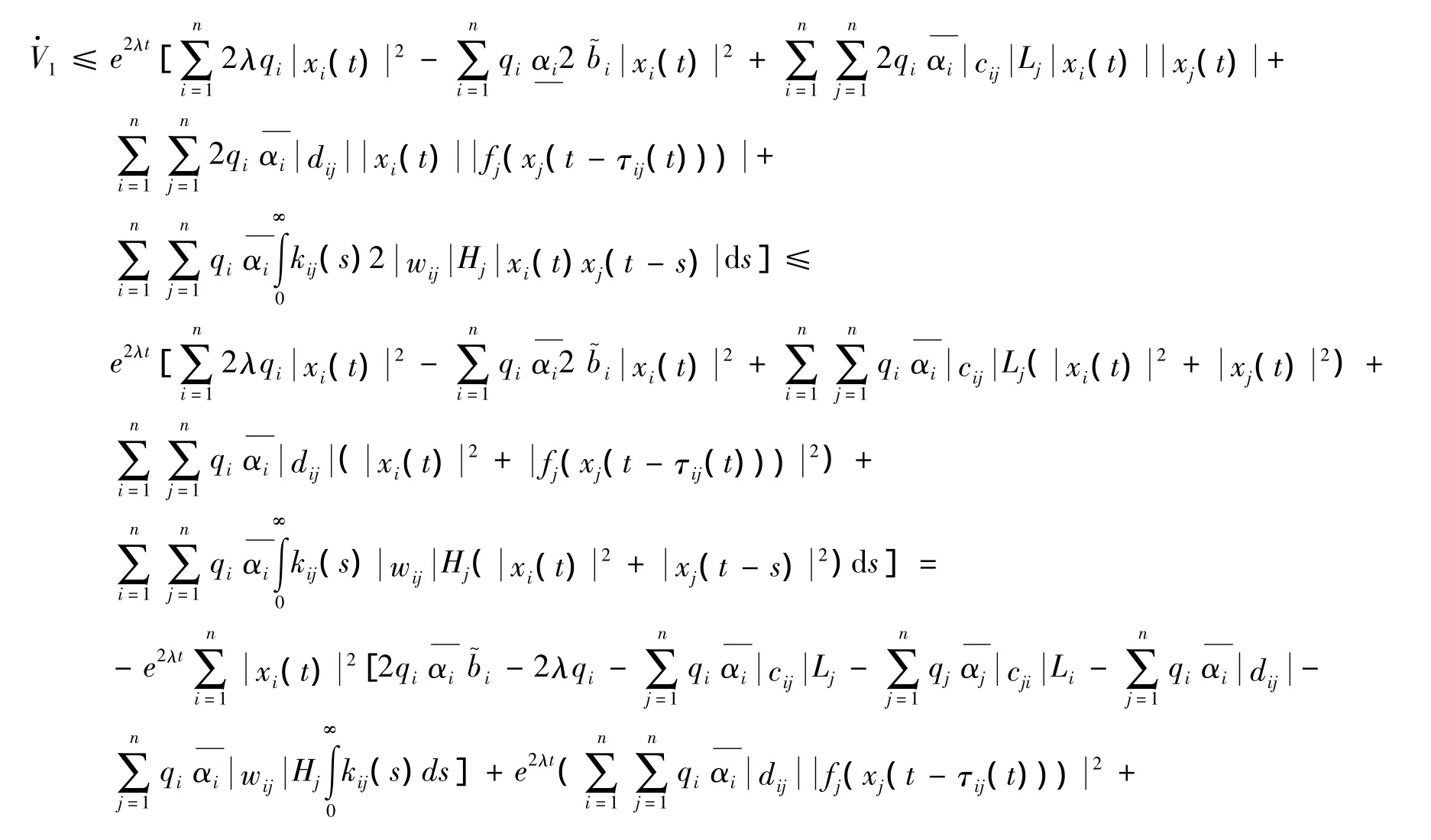
則

由V'＜0 知函數 V(t，x(t))是單調遞減的，有 V(t，x(t))≤V(t0，x(t0))，

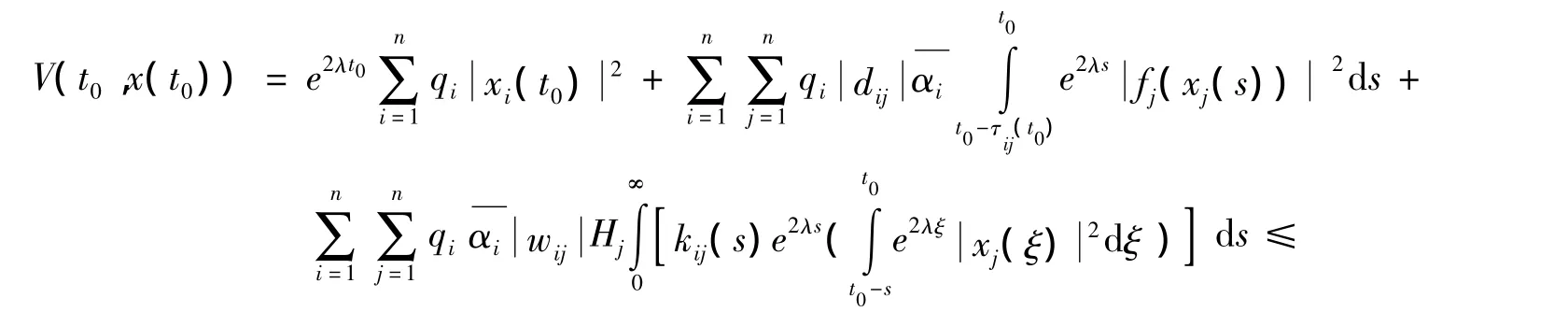
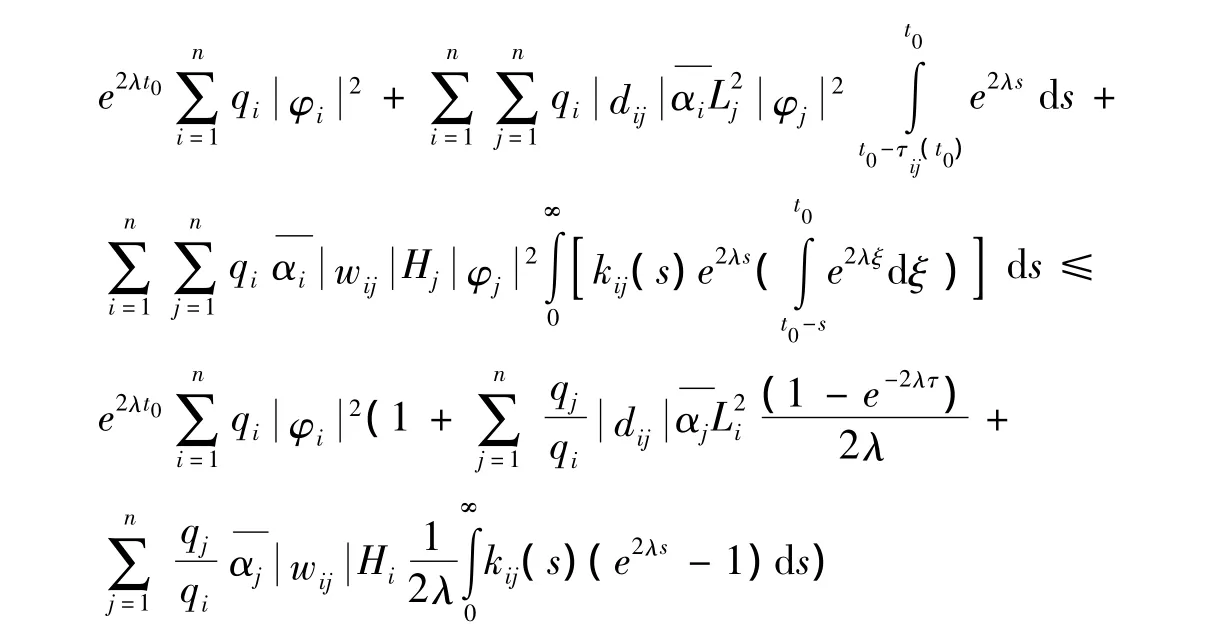
又因為

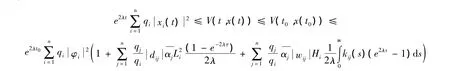
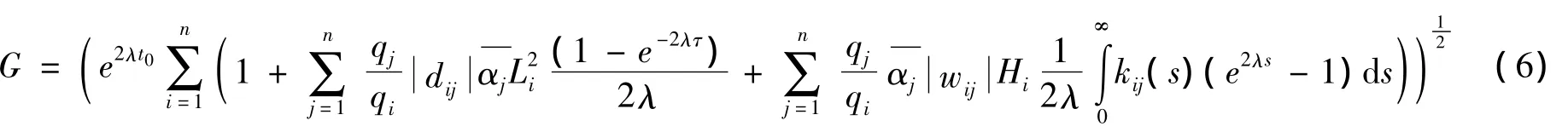
當t=tk時，根據假設4)～6)和指數穩定定義，有

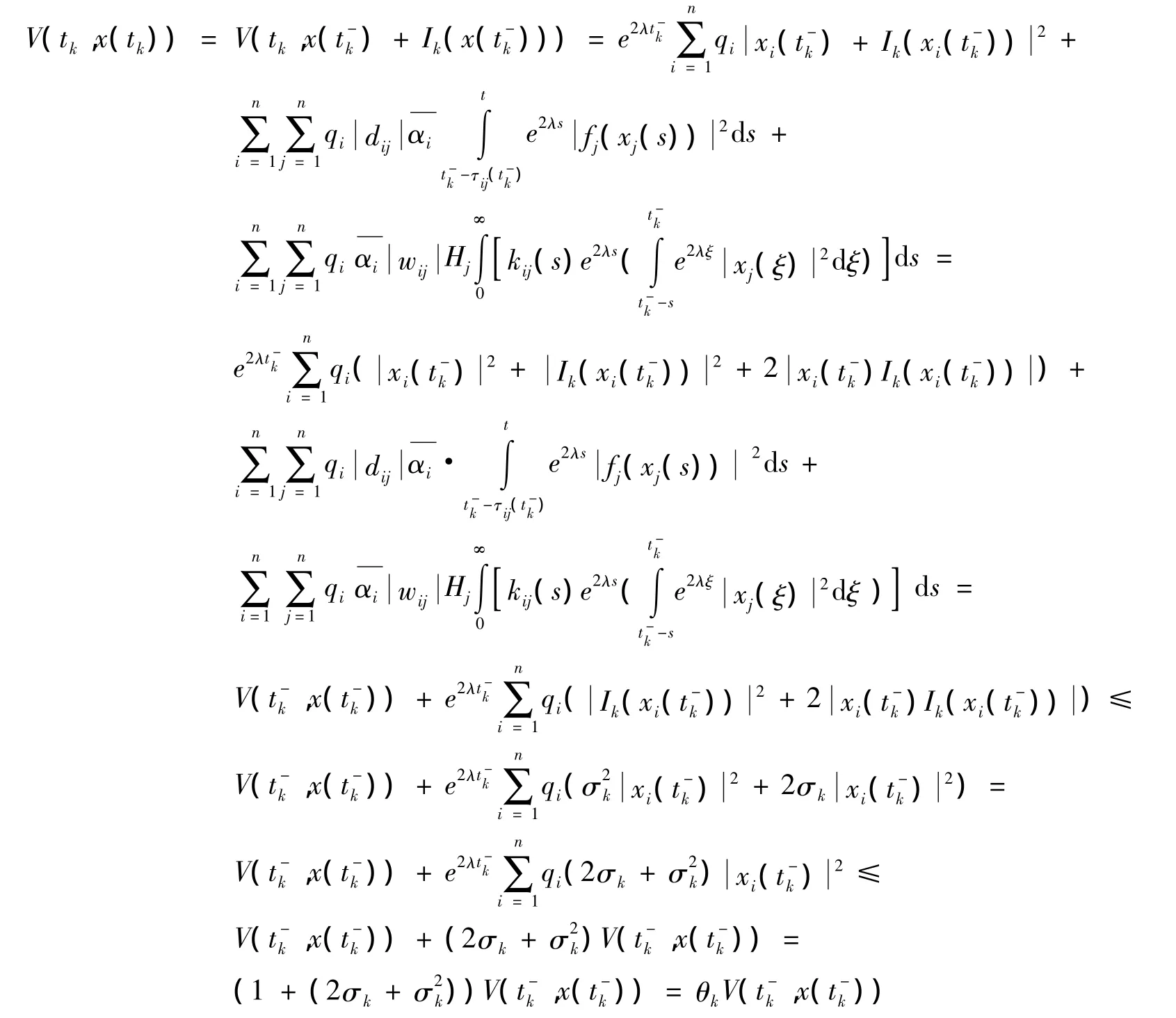
由模型的任意解x(t，t0，x0)可得

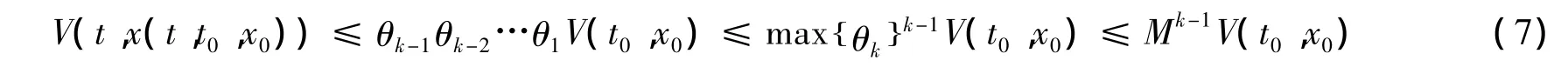
由于μτ≤inf{tk-tk-1}，μτ≤t1-t0，μτ≤t2-t1，…，μτ≤tk-1-tk-2，求和得 (k-1)μτ≤t1-t0+t2-t1+…

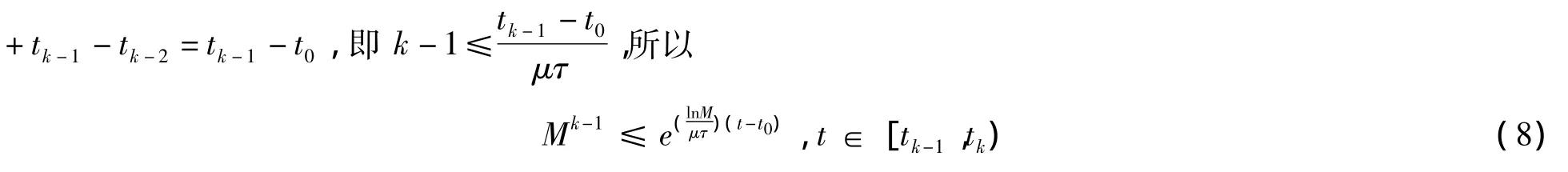
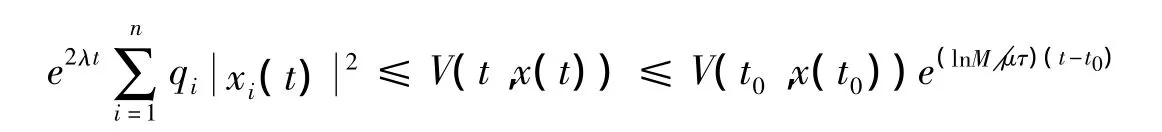
3 數值算例

考慮下面的系統

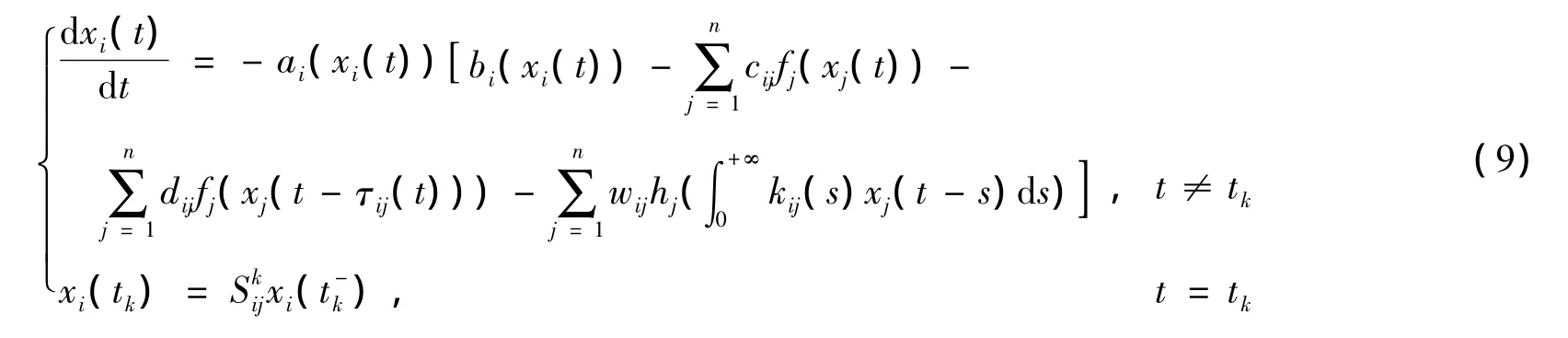
其中 a1(x1(t))=3+sinx1(t)，a2(x2(t))=4+cosx1(t)。

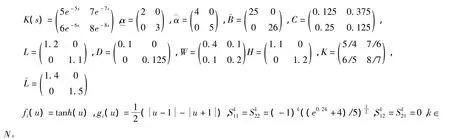
［1］Cohen M A，Grossberg S.Absolute stability of global pattern formation and parallel memory storage by competitive neural networks［J］.IEEE Trans Syst Man Cybern，1983，13(5):815-826.

［2］Liao X，Li C.Global attractivity of Cohen-Grossberg model with finite and infinite delays［J］.Math Anal Appl，2006，315(1):244-262.

［3］Huang T，Chan A，Huang Y，et al.Stability of Cohen-Grossberg neural networks with time varying delays［J］.Neural Networks，2007，20(8):868-873.

［4］Li T，Fei S.Stability analysis of Cohen-Grosserg neural networks with timevarying and distributed delays［J］.Neurocomputing，2008，71:1069-1081.

［5］Li K.Stability analysis for impulsive Cohen-Grossberg neural networks with time-varying delays and distributed delay［J］.Nonlinear Anal Real World Appl，2009，10(5):2784-2798.

［6］Zheng C D，Shan Q H，Wang Z.Novel stability criteria of Cohen-Grossberg neural networks with time-varying delays［J］.Int J Circuit Theory Appl，2012，40(3):221-235.

［7］Huang C X，Huang L H，He Y G.Mean square exponential stability of stochastic Cohen-Grossberg neural networks with unbounded distributed delays［J］.Discrete Dynamics in Nature and Society，2010(20):1-15.

［8］Wan L，Zhou Q.Exponential stability of stochastic reaction diffusion Cohen-Grossberg neural networks with delays［J］.Applied Mathematics and Computation，2008，206(2):818-824.

［9］Chen Y.Global Asymptotic Stability of Delayed Cohen-Grossberg Neural Networks［J］.IEEE Transactions on Circuit and Systems-I:Fundamental Theory and Applications，2006，53(2):351-357.

［10］Yang Z C，Xu D Y.Impulsive effects on stability of Cohen-Grossberg neural nettworks with variable delays［J］.Applied Mathematics and Cumputation，2006，177(1):63-78.

［11］Bai C Z.Stability analysis of Cohen-Grossberg BAM neural networks with delays and impulses［J］.Chaos，Solitons and Fractals，2008，35(2):263-267.

［12］Ping Z W，Lu J G.Global exponential stability of impulsive Cohen-Grossberg neural networks with continuously distributed delays［J］.Chaos，Solitons and Fractals，2009，41(1):164-174.

［13］Luo W P，Zhong S M，Yang J.Global exponential stability of impulsive Cohen-Grossberg neural networks with delays［J］.Chaos，Solitons and Fractals，2009，42(2):1084-1091.

［14］Li K L.Stability analysis for impulsive Cohen Grossberg neural networks with time varying delays and distributed delays［J］.Nonlinear Analysis:Real World Applications，2009，10(5):2784-2798.

［15］Lou X Y，Cui B T.Global exponential stability analysis of delayed Cohen-Grossberg neural networks with distributed delay［J］.International Journal of Systems Science，2007，38(7):601-609.

［16］Song Q K，Cao J D.Robust Stability in Cohen Grossberg Neural Network with both Time Varying and Distributed Delays［J］.Neural Process Lett，2008，27(2):179-196.

［17］Wang B X，Jian J G，Jiang M H.Stability in Lagrange sense for Cohen-Grossberg neural networks with time-varying delays and finite distributed delays［J］.Nonlinear AnaIysis:Hybrid Systems，2010，4(1):65-78.

［18］Wu W，Cui B T，Lou X Y.Global exponential stability of Cohen-Grossberg neural networks with distributed delays［J］.Mathematical and Computer Modelling，2008，47(9):868-873.

［19］Lu K，Xu D，Yang Z.Global attraction and stability for Cohen-Grossberg neural networks with delays［J］.Neural Networks，2006，19(10):1538-1549.