理解對應：從“標準圖形”到“變式圖形”

蔡美娟

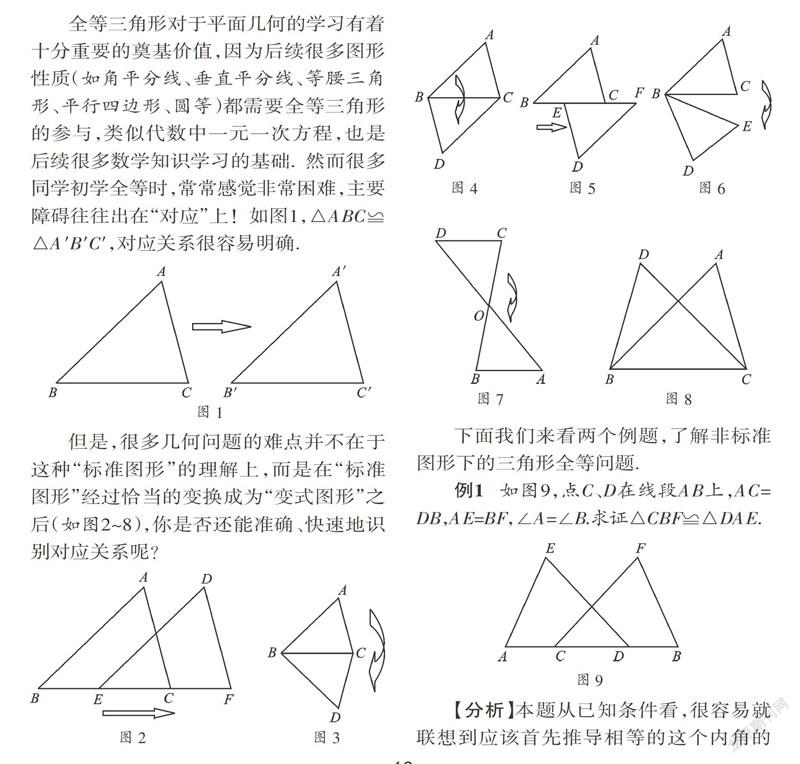
全等三角形對于平面幾何的學習有著十分重要的奠基價值，因為后續很多圖形性質（如角平分線、垂直平分線、等腰三角形、平行四邊形、圓等）都需要全等三角形的參與，類似代數中一元一次方程，也是后續很多數學知識學習的基礎.然而很多同學初學全等時，常常感覺非常困難，主要障礙往往出在“對應”上！如圖1，△ABC≌△A′B′C′，對應關系很容易明確.

但是，很多幾何問題的難點并不在于這種“標準圖形”的理解上，而是在“標準圖形”經過恰當的變換成為“變式圖形”之后（如圖2～8），你是否還能準確、快速地識別對應關系呢？

下面我們來看兩個例題，了解非標準圖形下的三角形全等問題.

例1 如圖9，點C、D在線段AB上，AC=DB，AE=BF，∠A=∠B.求證△CBF≌△DAE.

【分析】本題從已知條件看，很容易就聯想到應該首先推導相等的這個內角的另一條邊也是對應相等的，也就是AD=BC，然后再證明三角形全等.

證明：因為AC=DB（已知），

所以AC+CD=BD+CD，即AD=BC.

在△CBF和△DAE中，

AE=BF，

∠A=∠B，

AD=BC.

∴△CBF≌△DAE（SAS）.

例2 如圖10所示，AD∥BC，AD=CB，求證：△ADC≌△CBA.

【分析】本題是在兩個三角形有公共邊AC的情況下進行考慮的，也就是有兩組邊對應相等.若要根據SAS來判斷兩個三角形全等，應該首先推導以AC和AD的夾角∠2與CA和CB的夾角∠1也是對應相等的，然后再證明三角形全等.

證明：因為AD∥BC，

所以∠1=∠2.

在△ADC和△CBA中，

AD=CB，

∠1=∠2，

AC=CA.

所以△ADC≌△CBA（SAS）.

【解后反思】如果再由證得的全等三角形出發，同學們還能得出該四邊形ABCD中對邊AB、CD有怎樣的數量關系、位置關系嗎？

（作者單位：江蘇省海安縣李堡鎮初級中學）