基于隨機積分的非線性濾波跟蹤算法?

(電子科技大學電子工程學院,四川成都611731)

0 引言

雷達系統中常會遇到非線性狀態估計問題,例如目標再入問題[1],目標運動復雜,其狀態方程是非線性函數;或混合坐標系下目標跟蹤,其量測方程是非線性函數等[2]。解決非線性狀態估計問題,貝葉斯濾波結構為系統狀態估計提供了一種遞歸結構。與線性系統直接利用卡爾曼濾波遞歸求得最優解不同[3],在貝葉斯濾波結構下很難對非線性系統實現遞歸求解。只有獲得了系統狀態的后驗概率分布的完整描述才能獲得非線性狀態估計問題的最優解[4],然而很少情況下能精確描述后驗概率。

因此,人們提出了大量的次優濾波算法,EKF濾波算法是解決非線性濾波的最常用的方法[5],該算法通過對非線性函數一階泰勒級數展開將非線性問題轉化為線性問題,但在線性化過程中引入了模型誤差,而且需要計算Jacobian矩陣,增大了計算量,也容易出現濾波發散問題,因此在實際應用中受到了很大的限制。隨后Julier等人提出一種不敏卡爾曼濾波(UKF)算法[6-7]。UKF對狀態向量的PDF進行近似化,表現為選取一系列的采樣點通過非線性函數傳播,捕獲非線性函數的統計特性,得到后驗均值和協方差精確達到2階。UKF在模型參數估計、目標跟蹤等方面都得到了較廣泛的應用,但是當狀態維數增加或系統非線性強時,UKF濾波會出現精度急劇下甚至發散等問題。2009年,加拿大學者Arasaratnam提出一種新的貝葉斯近似濾波算法——容積卡爾曼濾波算法(CKF)[8],該算法為非線性估計問題提出了一種新的實現方式,CKF應用球面徑向容積準則對函數積分進行近似,解決了貝葉斯濾波結構下積分問題。近年來,CKF已經應用到了非線性濾波估計上,例如目標跟蹤和數據融合[9-10]。該算法在一定程度上克服了EKF和UKF在強非線性系統中的應用局限性,但是隨著模型狀態維數的增加或系統非線性增強時,CKF的跟蹤性能下降。

針對存在的問題,本文提出一種新的非線性濾波跟蹤算法——隨機球面徑向積分濾波算法(SSIF)。該算法利用隨機球面徑向準則近似積分方程來實現濾波遞歸,首先利用隨機球面積分規則近似球面積分,再利用隨機徑向積分規則近似徑向積分。通過該方法可以消除系統誤差提升系統的跟蹤精度和濾波穩定度,具有更快的收斂速度和更優的數值逼近能力。通過蒙特卡洛仿真實驗表明,利用本文提出的非線性濾波算法對雷達系統的非線性目標跟蹤整體性能有明顯提升。

1 系統描述和問題

考慮非線性離散隨機系統[2,6]

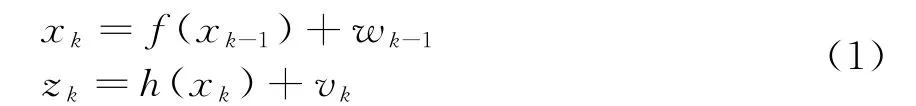
式中,狀態x k∈?n,n表示狀態維數;z k∈?m,m表示量測維數;w k,v k分別是相互獨立的過程噪聲和觀測噪聲,滿足均值為0、協方差分別為Q k,R k的高斯分布。

假設在k-1時刻狀態后驗概率函數為p(x k-1|z1:k-1),則預測狀態的概率密度函數p(x k|z1:k-1)可表示為

根據所接收到的量測z k,更新后驗概率

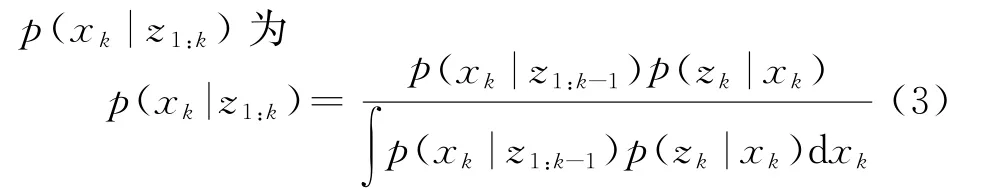
式中,p(z k|x k)為似然函數。

假設狀態預測概率密度函數p(x k|z1:k-1)和似然函數p(z k|x k)均為高斯函數,因此后驗概率密度函數p(x k|z1:k)仍是高斯函數,確定該密度函數只需要計算這些高斯概率密度函數的均值和方程即可。對于式(1)所描述的系統,貝葉斯結構濾波器可概括為兩步:預測和更新[8]。

(1)預測

第1步:初始化,在時間k=0時,定義先驗概率p(x0|z-1)=p(x0),相應的均值和方差分別為

第2步:計算狀態均值x k|k-1和方差p k|k-1

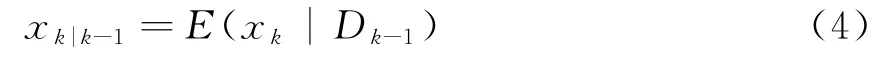
式中,D k-1表示過去輸入的量測數據。

將式(4)代入式(1),則有

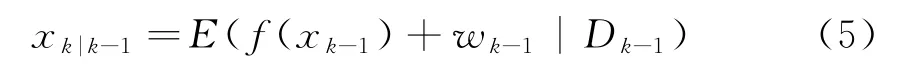
由于w k是0均值不相關的高斯白噪聲,因此有

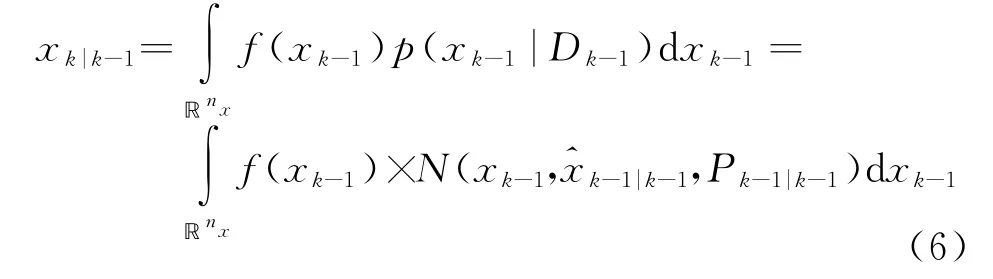
相應的誤差協方差

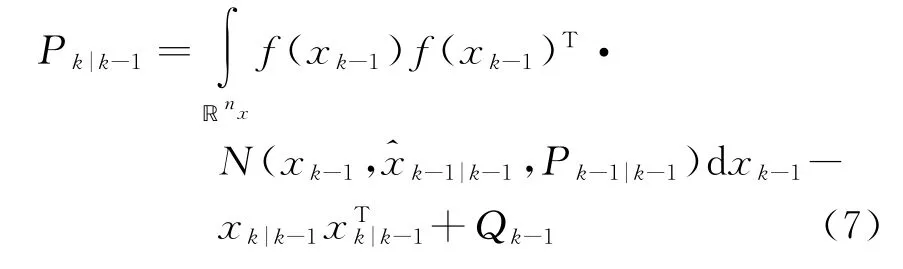
(2)更新

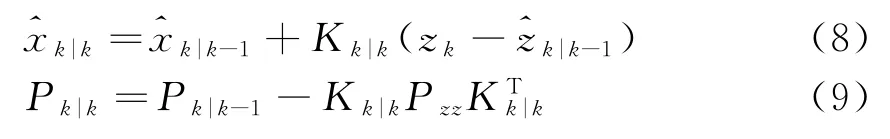
式中,

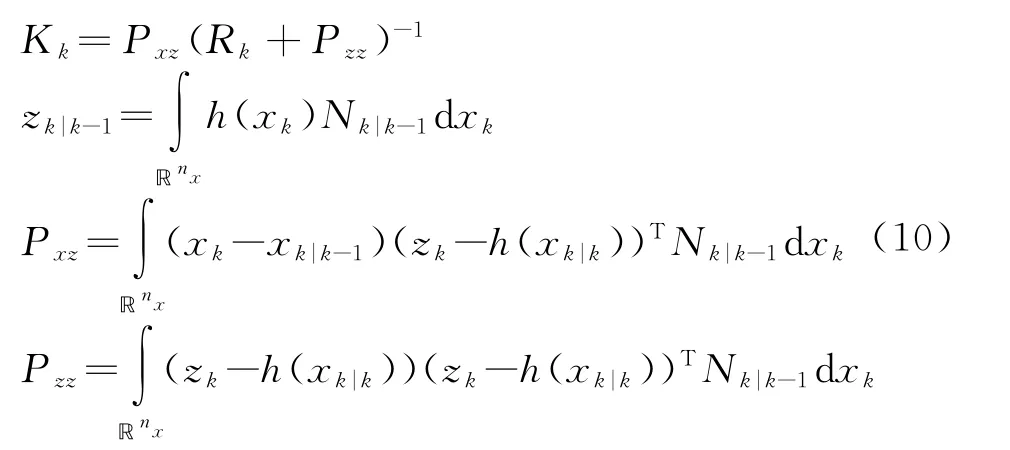
根據上述貝葉斯濾波結構,可以發現問題關鍵在于計算多維函數積分,被積函數的形式為非線性函數乘以高斯概率函數[11]。實現對多維函數積分難度較大,因此需要有效的數值積分對其近似。近年來涌現了大量的對該積分近似的方法,如EKF,UKF和CKF等,由于這些方法存在精度差和容易發散等問題。因此本文提出一種更為有效的積分近似算法,該算法利用隨機球面積分規則和隨機徑向積分規則近似積分函數來實現濾波遞歸。

2 隨機球面徑向積分濾波器(SSIF)

在高斯背景假設下,貝葉斯濾波結構下函數的積分形式都可表示為

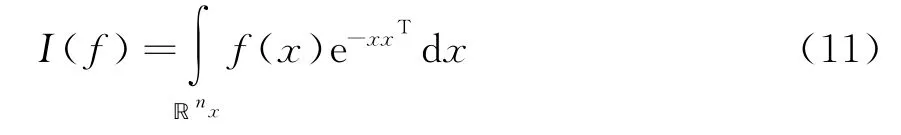
式中,f(·)表示任意函數。

很難解決式(11)的積分,因此需要找出一種方法近似該積分。一種數值積分近似的方法是通過找到一組權值w i和采樣點x i,利用權值和被積函數的加權可近似該積分函數:

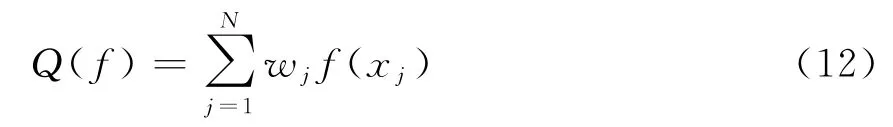
式中,N表示采樣點總數。

利用球面徑向變換規則對式(11)進行變換,利用x=ry替換,且yTy=1,r=x xT,因此式(11)表示為

式中,U n={y∈?n|yTy=1},式(13)可分解為

因此對式(11)的積分近似轉化為對式(14)的積分進行近似。

(1)隨機球面積分規則

對球面積分選擇適合的積分準則,通過旋轉隨機積分準則,將所得到的值加權來近似球面積分[12-13]

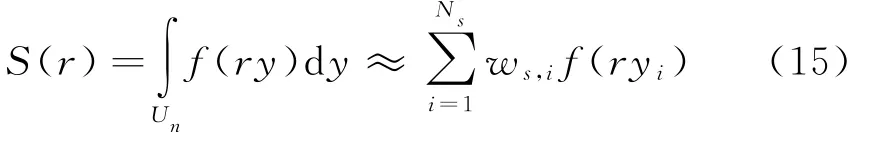
其中,對于所有的i有

作為一個球面積分近似規則,在單位球面U n上近似積分函數f(y),且yTy=1;假設Q是n×n的正交矩陣,則

由于‖Qy‖=‖y‖,所以式(16)同樣是對球面U n的一個積分規則,如果式(15)是3階函數,則式(16)同樣是一個3階函數,假如Q是服從均勻分布,則S Q為球面U n的無偏積分規則。

因此,在3階隨機積分規則下,式(16)可近似為

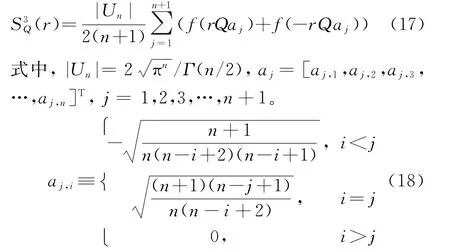
(2)隨機徑向積分規則

通過下面的公式來近似估計N r點的徑向積分[12]:

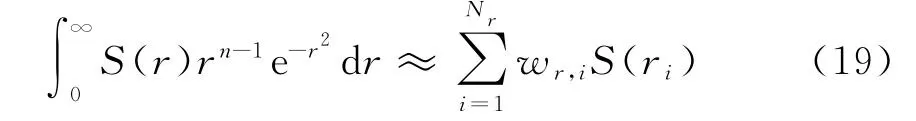
給定點{r i}和權值{w i}就可以確定該積分,點{r i}隨機選取以保證式(19)的無偏性,設置r0=0,點集的聯合概率密度函數p(r1,r2,r3,…,r n)如式(20)所示。

則函數積分I(f)用3階隨機徑向積分近似為

(3)隨機球面徑向積分規則

將隨機球面規則和隨機徑向規則聯合起來成為一種近似I(f)的簡單隨機積分規則——隨機球面徑向積分規則。本文提出的新積分規則能有效近似函數積分,且保證估計的無偏性。函數的積分可近似為SR Q,r(f),具體形式為

因此,跟蹤3階隨機球面徑向積分規則:

具體的3階隨機球面徑向規則積分算法[13]如下:

第1步 設置誤差容忍度ε,最大迭代次數Nmax,采樣點數n。

第2步 設置迭代次數N=0,初始積分值I=,初始化積分均方誤差,估計均方誤差S x,且,計算F0=f(0)。

第3步 重復迭代

(a)設置N=N+1,SR q,r=0;

(b)產生n x×n x維的均勻分布的隨機正交矩陣Q;

(c)產生隨機數r～Chi(m+2);

(d)從j=1,2,…,n x循環,SR q,r=SR q,r+

第4步 輸出I(f)≈I,即I為積分公式I(f)的近似值。

(4)隨機球面徑向積分濾波器的設計

利用3階隨機球面徑向積分規則算法來近似貝葉斯濾波器結構中的積分,形成一種簡單的隨機積分濾波器(SSIF)。狀態預測式(6)～(7)利用式(26)計算,計算預測狀態x k+1|k時,p(x)和f(x)分別用p(x k|z k)和f(x k)代替;計算預測狀態協方差矩陣P k+1|k時,利用f(x k)f(x k)T代替f(x)。同理,可以估計式(10)。

SSIF濾波跟蹤算法步驟如下:

第1步 設置時間k=0,參數Nmax,誤差容忍度ε,采樣點數n,初始化狀態均值和協方差矩陣分別為x0|0=E(x0)=x0,p0|0=E(p0)=p0。

第2步 狀態預測

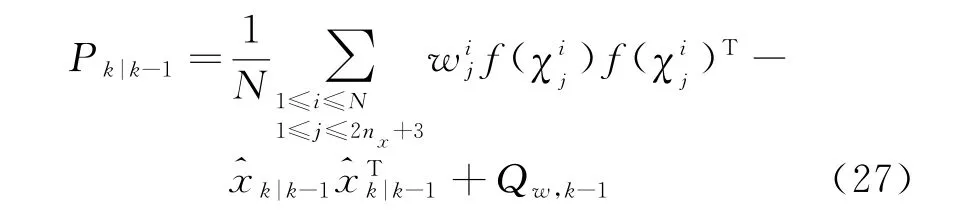
第3步 量測更新

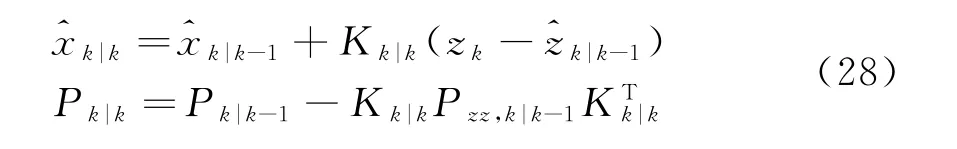
完成更新,令k=k+1,繼續步驟2。

3 仿真實驗及分析

本文所提的非線性濾波算法與不敏卡爾曼濾波算法(UKF)和改進的容積卡爾曼濾波算法(SCKF)在非線性跟蹤系統中進行比較,并對結果進行分析。假設目標勻加速機動飛行,目標狀態為(在 三 維 空 間 中它包含了目標各個方向的位置、速度和加速度,因此n x=9)。直角坐標系下狀態方程為

式中,w k表示均值為零的高斯白噪聲,協方差矩陣所以Q=q s·diag(Q1,Q1,Q1),q s為功率譜密度,且Q1為

F ca=diag[I3?F],T表示采樣時間間隔,I3表示3×3的單位陣,?表示Kronecker乘法。

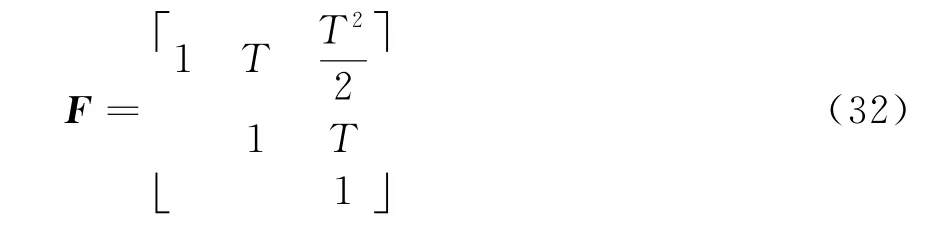
雷達觀察到的目標量測為極坐標系下數據,因此第k時刻的量測z k為

式中,v k為零均值的高斯白噪聲,其協方差矩陣,且非線性量測方程h(x k)為

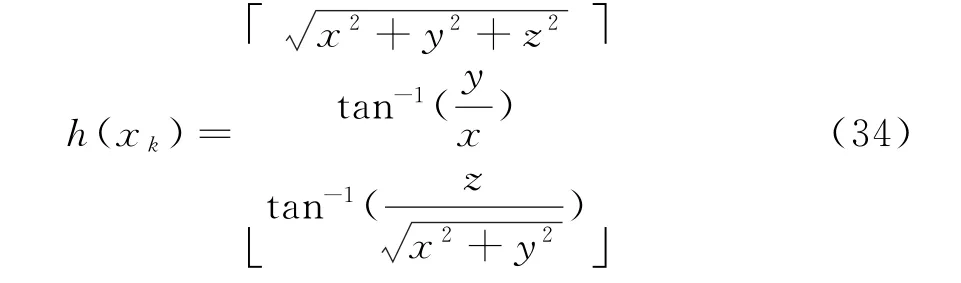
假設目標在0～25 s內一直作勻加速運動,雷達位于坐標原點位置,目標初始位置為[x,y,z]=[8 km,9 km,1 km]T,速 度 為150 m/s,150 m/s],加 速 度 為6 m/s2,15 m/s2],采樣時間間隔T=0.5 s,總跟蹤時間t=25s,距離均方根誤差δr=10 m,俯仰角和方位角均方根誤差分別為δθ=δφ=2°,功率譜密度q s=0.1 m2·s-1,最大迭代次數Nmax=50,誤差容忍度ε=0.5,進行500次蒙特卡洛仿真實驗,位置的均方根誤差定義為

式中,x,y,z為目標真實坐標位置為目標估計位置,M為蒙特卡洛仿真實驗次數。

圖1為勻加速機動目標運動軌跡,通過蒙特卡洛仿真實驗,得到目標跟蹤的位置均方根誤差曲線圖(圖2)、速度均方根誤差曲線圖(圖3)、加速度均方根誤差曲線圖(圖4)和不同參數下新算法對目標的跟蹤性能(表1)。仿真中分別利用UKF和CKF濾波算法以及本文提出的非線性濾波算法對非線性雷達系統進行跟蹤估計,從圖2、圖3和圖4可以看出,本文所提的非線性濾波算法具有更高的跟蹤精度,對目標加速度、速度和位置的估計更為精確,穩定性更強,使跟蹤的整體跟蹤性能得到一定提升。從表1可以得出,隨著迭代次數N的增加或誤差容忍度ε的減小,新算法的性能有進一步的提高,位置和速度的均方根誤差都有一定的提升。但由于迭代次數N增加,計算量相應的會增加,因此需要綜合考慮計算量和性能,N的取值不宜過大。

表1 不同參數下跟蹤結果

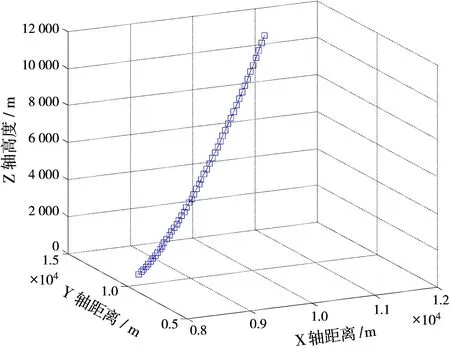
圖1 目標運動軌跡圖

圖2 位置均方根誤差曲線圖

圖3 速度均方根誤差曲線圖

圖4 加速度均方根誤差曲線圖

4 結束語

本文主要提出一種新的非線性濾波算法——隨機球面徑向積分濾波算法(SSIF),該算法基于隨機積分規則,即利用隨機球面積分規則和隨機徑向積分規則實現對貝葉斯結構下函數積分的近似。對雷達系統的非線性目標跟蹤中,相較于傳統的非線性濾波跟蹤算法,本文提出的濾波算法消除了系統誤差,提高了跟蹤精度,且有效地抑制了非線性濾波易出現發散的問題,提升了跟蹤的穩定性。通過蒙特卡洛仿真實驗證明,該算法對非線性目標跟蹤性能有明顯的提升。

[1]STRAKA O,DUNIK J,SIMANDL M.Randomized Unscented Kalman Filter in Target Tracking[C]∥Proceedings of the 15th International Conference on Information Fusion,Singapore:[s.n.],2012:503-510.

[2]GARCíA-FERNáNDEZ A F,MORELANDE M R,GRAJAL J.Nonlinear Filtering Update Phase via the Single Point Truncated Unscented Kalman Filter[C]∥2011 Proceedings of the 14th International Conference on Information Fusion,Chicago,IL:IEEE,2011:1-8.

[3]金亮亮,劉亞云.一種改進自適應機動目標跟蹤算法[J].雷達科學與技術,2014,12(1):97-100.

[4]N?RGAARD M,POULSEN N K,RAVN O.New Developments in State Estimation for Nonlinear Systems[J].Automatica,2000,36(11):1627-1638.

[5]GUSTAFSSON F,HENDEBY G.Some Relations Between Extended and Unscented Kalman Filters[J].IEEE Trans on Signal Processing,2012,60(2):545-555.

[6]JULIER S J,UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[7]劉妹琴,湯曉芳,鄭世友,等.基于RUKF-IMM的非線性系統濾波[J].華中科技大學學報,2013,41(5):57-63.

[8]ARASARATNAM I,HAYKIN S.Cubature Kalman Filters[J].IEEE Trans on Automatic Control,2009,54(6):1254-1269.

[9]DAHMANNI Mohammed,MECHE Abdelkrim,KECHE Mokhtar.Reduced Cubature Kalman Filtering Applied to Target Tracking[C]∥2ndInternational Conference on Control,Instrumentation and Automation,[S.l.]:[s.n.],2011:1097-1101.

[10]霍光,李冬海,李晶.機動目標單站無源定位中的量測更新CKF-IMM算法[J].電子信息對抗技術,2013,28(5):33-38.

[11]ARASARATNAM I,HAYKIN S,ELLIOTT R J.Discrete-Time Nonlinear Filtering Algorithms Using Gauss-Hermite Quadrature[J].Proceedings of the IEEE,2007,95(5):953-977.

[12]STROUD A H.Approximate Calculation of Multiple Integrals[M].NJ:Prentice-Hall,1971.

[13]GENZ A,MONAHAN J.Stochastic Integration Rules for Infinite Regions[J].SIAM Journal on Scientific Computation,1998,19(2):426-439.