雙參數(shù)算子半群Yosida 的逼近性質(zhì)

倉(cāng)定幫， 陳 藏， 閆守峰

(1.華北科技學(xué)院 基礎(chǔ)部，北京101601;2.華北科技學(xué)院 教務(wù)處，北京101601)

20 世紀(jì)中期，為了解決偏微分方程的初值問(wèn)題，以E.Hille 與K.Yosida 為代表的一些數(shù)學(xué)家提出了Banach 空間上強(qiáng)連續(xù)半群理論［1-2］。現(xiàn)今，強(qiáng)連續(xù)半群的理論已經(jīng)成為許多領(lǐng)域(除了傳統(tǒng)的偏微分方程和隨機(jī)過(guò)程外，還包括量子力學(xué)、無(wú)窮維控制理論、積分-微分方程、泛函微分方程及無(wú)窮維動(dòng)力系統(tǒng)等)的重要工具。近年來(lái)，雙參數(shù)算子半群由于與下面的雙參數(shù)抽象柯西問(wèn)題(ACP)的密切關(guān)系重新得到了很多學(xué)者的重視與研究［3-6］。

其中，Hi:D(Hi)?X →X i = 1，2 為線性算子。

文中對(duì)雙參數(shù)算子半群展開(kāi)進(jìn)一步探討，給出了Banach 空間上雙參數(shù)算子半群生成元的Yosida逼近定義，得到了雙參數(shù)算子半群可微性與一致算子拓?fù)湎碌倪B續(xù)性的充要條件，對(duì)單參數(shù)算子半群的相關(guān)研究方法加以推廣。

1 定義與引理

定義1［4］設(shè)L 為Banach 空間，T(s，t)，s ≥0，t ≥0，為L(zhǎng) 中的有界線性算子，?s1，s2，t1，t2≥0，T(s，t)稱為雙參數(shù)半群。如果滿足:

1)T(0，0)= I，I 為單位算子;

2)T(s1+ t1，s2+ t2)= T(s1，t1)T(s2，t2)，

若存在常數(shù)ω，M ＞0，使得‖T(s，t)‖≤Meω(s+t)成立，則稱雙參數(shù)半群是指數(shù)有界的。

引理1［4］雙參數(shù)算子半群T(s，t)的無(wú)窮小生成元是變換R+2→B(L)，由下面的表達(dá)式定義:

其中，A1，A2定義如下:

并且

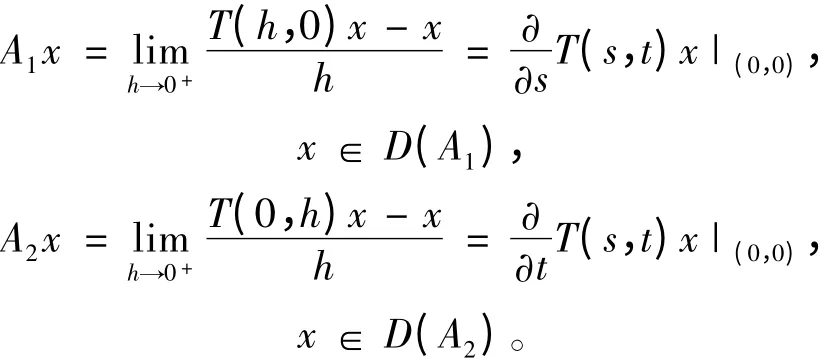
同時(shí)還有

及

引理2［4］設(shè)T(s，t)為Banach 空間L 中的雙參數(shù)算子半群，無(wú)窮小生成元為(A1，A2)，若

且

則有

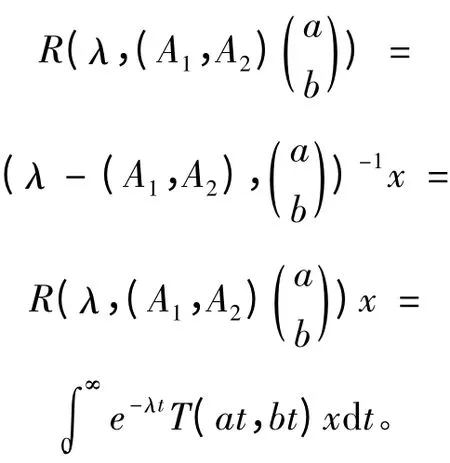
顯然，可以發(fā)現(xiàn)若T(s，t)是指數(shù)有界的，則有

定義2 設(shè)T(s，t)為Banach 空間L 中的雙參數(shù)算子半群，無(wú)窮小生成元為(A1，A2)，定義

稱Lλ為Yosida 逼近。

2 主要結(jié)論

定理1 設(shè)T(s，t)為Banach 空間L 中的雙參數(shù)算子半群，則

其Yosida 逼近滿足下列結(jié)論:

證 當(dāng)λ →+ ∞時(shí)，

再根據(jù)Yosida 逼近的定義可知:

定理2 設(shè)T(s，t)為Banach 空間L 中的雙參數(shù)算子半常數(shù)群，無(wú)窮小生成元為(A1，A2)，A1，A2均為稠定閉算子，Lλ為Yosida 逼近，若T(s，t)是強(qiáng)連續(xù)的，則T(s，t)在點(diǎn)(s，t)s≥s0，t≥t0可微的充要條件是存在常數(shù)M ＞0，使得對(duì)

成立。

證 先證明必要性。假設(shè)T(s，t)在點(diǎn)(s，t)s≥s0，t≥t0是可微的，則

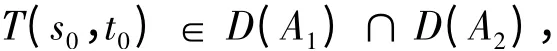
由定理1 可得

從而存在常數(shù)Mx＞0，使得

成立。再根據(jù)共鳴定理可知，

成立。

下證充分性。假設(shè)(A1，A2)為雙參數(shù)算子半群T(s，t)的生成元，并且存在常數(shù)M ＞0，使得對(duì)

成立。再據(jù)定理1 可知

又因?yàn)锳1，A2是稠密算子，可以證明上面的極限對(duì)任意得到x ∈X 成立。又因?yàn)?/p>

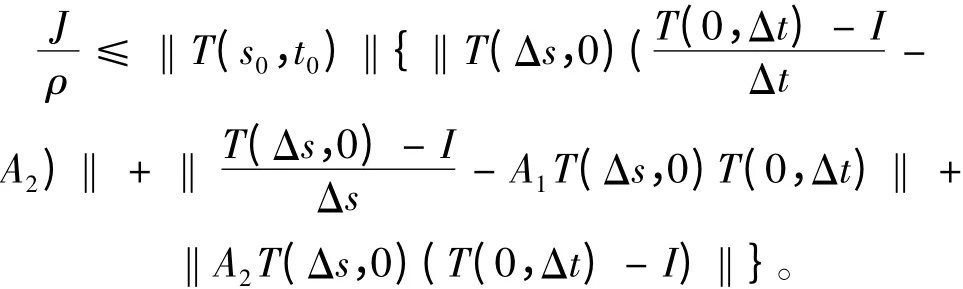
根據(jù)雙參數(shù)半群的連續(xù)性及其指數(shù)有界性，可以看出

即T(s，t)在點(diǎn)(s，t)s≥s0，t≥t0是可微的。

推論1 設(shè)T(s，t)為Banach 空間L 中的雙參數(shù)算子半常數(shù)群，無(wú)窮小生成元為(A1，A2)，A1，A2均為稠定閉算子，Lλ為Yosida 逼近，若T(s，t)是強(qiáng)連續(xù)的，且對(duì)

成立，則T(s，t)在點(diǎn)(s，t)可微，并且

定理3 設(shè)T(s，t)為Banach 空間L 中的指數(shù)有界的雙參數(shù)算子半常數(shù)群，無(wú)窮小生成元為(A1，A2)，A1，A2均為稠定閉算子，Lλ為Yosida 逼近，則T(s，t)一致算子拓?fù)溥B續(xù)的充要條件為

證 先證明必要性。因?yàn)殡p參數(shù)半群指數(shù)有界，即‖T(s，t)‖≤Meω(s+t)，所以由引理1 可得

從而當(dāng)λ ＞max{ω(A1)，ω(A2)}時(shí)，對(duì)δ ＞0，有

因此

又由δ ＞0 的任意性和T(s，t)一致算子拓?fù)溥B續(xù)性可知

成立。

則對(duì)?ε ＞0，存在常數(shù)λ0＞0 使得下面不等式

成立。

令0 ＜Δt ＜ε，0 ＜Δs ＜ε，因?yàn)?/p>

其中

又有

所以T(s，t)是一致算子拓?fù)溥B續(xù)的。

［1］Hille E.Representation of one-parameter semigroups of linear transformations［J］.Nat Acad Sci，1942，28:175-178.

［2］Yosida K.On the differentiability and representation of one-parameter semigroups of linear operators［J］.J Math Soc Japan，1948，1:15-21.

［3］Arora S，Sharda S.On two parameter semigroup of operator［D］.New Delhi:University of Delhi，1990:147-153.

［4］Sharif S A，Khallr.On the generator of two parameter semigroups［J］.Applied Mathematics and Computation，2004，156(2):403-414.

［5］Janfada M.On two-parameter regularized semigroups and the Cauchy problem［J］.Bull Austral Math，2004，69:383-394.

［6］Khanehgir M，Janfada M，Niknam A.Two-parameter integrated semigroups and two-parameter abstract Cauchy problems［J］.Jour of Inst of Math and Comp Sci (Math)，2005，1(18):1-12.