多因素約束韋伯型設施的選址問題

李 磊， 陳文斌

(江南大學商學院，江蘇 無錫214122)

隨著經濟社會的發展，設施選址問題日益成為運籌學和計算應用領域的研究核心。設施選址問題的主要思想是在客戶、資源、目的等條件已知的情況下，確定一個或者多個新設施點，最大化使用資源［1］。通常需要數學、管理學、計算機、金融學等多學科知識的融合來建立模型，解決問題，其研究理論日漸成熟和完善。

選址問題是一個古老又經典的問題，早在1634年，法國數學家Fermat提出了在一個平面上有任意3點，試求第4點，使之到這3個點構成的距離最短。該問題在17世紀由意大利數學家托里切利解決，這個點被稱為“費馬點”。1750年，辛普森(T.Simpson)提出了一種加權情形:若 A1，A2，A3，為平面上給定的3個點，又wi＞ 0(i=1，2，3)，求平面上一點A0，使∑wi‖A1A0‖|最小。19世紀初，瑞士幾何學家Steiner將此問題推廣到n個點:求平面上一點至已給n個點的距離之和最小，此問題稱為斯坦納問題［2］。1909年德國經濟學家韋伯以斯坦納問題為理論模型，首先提出了設施選址問題，其研究對象為在工業區內建立一個倉庫使得到不同需求方的總距離最小［3］。

近年來，伴隨著計算機技術的發展，智能算法在設施選址問題上做出了巨大貢獻。Harry Venables和Alfredo Moscardini提出搜索啟發性算法，采用蟻群優化(ACO)進行設備隨機選擇，得到CFCLP問題的近似最優解［4］。Lyamine Bouhafs等人采用模擬退火算法和蟻群算法解決選址行程問題(LRP)。Blas Pelegrín等人設計了一個改進的遺傳算法，在位置集合m中選擇一系列的廠址，以滿足假定條件下的最優。對于算法的有效性和效率性進行了業績評價。2004年李彤提出模擬植物生長算法，一種源于植物向光性機理的智能優化算法。目前關于單點設施選址的研究日趨成熟，但是對于單點多因素制約問題由于其本身的復雜性，始終沒有得到實質上的突破。在現實問題中設施選址問題往往受到多種因素制約。因此，文中旨在運用植物生長算法，建立韋伯模型，解決多因素制約問題。

韋伯型設施選址問題是運籌學中一個著名問題，特別是對于位置問題進入了深度研究分析。韋伯設施選址涉及定位一套設施并且分配它們的能力來滿足一組客戶需求，以求總運輸成本最小化。在韋伯模型中，工廠、倉庫、配送中心都可以構成設施，而超市、零售商可以被視為客戶。韋伯模型的數學表達式為

式中，aj(j=1，2，…，m)是第 j個用戶的位置，x=(x1，x2，…，xn)是有界閉凸區域，xi為第 i個設施的待定位置，wij是第i個設施到第j個用戶的權重，‖xi-aj‖是xi到a的范數距離，本問題采用歐式距離。

1 算法理論

1.1 植物生長模擬算法

植物生長模擬算法(Plant Growth Simulation Algorithm，PGSA)是由李彤提出的，是一種借鑒于植物向光性機理原理的智能優化算法，最初是為了解決整數規劃問題。由于PGSA對參數的確定極為簡單和寬松，因而被國內外學者大量使用和研究完善。PGSA是由形態素濃度決定的方向性和隨機性平衡比較理性的啟發式搜索機制，在較短的運算時間內，以較快的計算速度尋找到全局最優解［6-7］。

假設M表示樹干的長度，樹干上具有T個生長點表示為 SM=(SM1，SM2，…，SMT)，每個生長點各自的形態素濃度值表示為 PM=(PM1，PM2，…，PMT);設樹枝的單位長度m(m＜M)上的r個生長點表示為sm=(sm1，sm2，…，smr)，每個生長點各自的形態素濃度值是 pm=(pm1，pm2，…，pmr)。計算樹干與樹枝上生長點形態素濃度值為

其中，x0表示初始可行解(即樹根)，f(*)是目標函數值(即生長點的背光函數)，f(*)的函數值隨著生長點的受光程度的增大而減小，符合生長點形態素濃度值與其各自所受的光照條件及樹根光照條件的對應關系。

由式(2)，(3)可得

即所有的生長點形態素濃度之和為1。確定了形態素濃度后，濃度值高的生長點優先生長機會大。若樹干、枝干上共包含K+q個生長點，即(x1，x2，…，xK+q)，由式(2)，(3)知每個生長點形態素濃度值為(p1，p2，…，pK+q)。由式(4)可證p1+p2+ … +pK+q=1。接著隨機生成一個［0，1］區間的值，用來作為下一個新生長點，循環生長［7-9］。

1.2 PGSA的改進

在傳統的PGSA算法求解中，枝干長度根據有界閉箱范圍來確定。但是現實中，可行域空間的差異性很大，搜索步長根據具體問題主觀設定。當可行域空間較大時，搜索步長的確定較為困難，如果設置不當可能導致無法找到全局最優解。有限元法視整個系統為有限個單元共同連接形成的幾何體，劃分單元以數字對系統進行描述。為了改進植物生長模擬算法，引入有限元方法自動生成合理的初始網格，建立生長結點的拓撲關系。以此初始生長點結構為基礎的模擬計算，使初始點的確定更加簡便。如圖1所示。謝爾賓斯基地毯的特點是:處處有洞但連續，面積為0但周長無窮大。

將謝爾賓斯基地毯作為約束條件的有界閉箱，以地毯中正方形的4個頂點作為有限元網格的結點，可將有限元網格結點作為模擬植物生長的初始生長點，唯一需要改變的是，在去除掉的部分內部，仍需按照分形原則進行處理并建立初始生長點。采用謝爾賓斯基地毯的結構確定生長點，對于解決可行域空間很大、全局最優解和局部最優解眾多的非線性規劃問題效果良好。

圖1 謝爾賓斯基地毯Fig.1 Sher Pinsky carpet

2 選址影響因素分析及權重的確定

以超市配送中心選址為例，在超市供應鏈管理中，配送中心的選址是最重要的部分，與庫存、配送以及供應網絡都有密切關系，故此超市配送中心的選址受到多種因素制約。實際中通常應該考慮以下的影響因素:

1)配送中心的選址要盡可能使配送總距離最短，建立損耗最小的配送網絡，減少配送成本和配送時間。

2)配送中心要盡可能靠近人流量多、配送周期短的超市。

3)配送中心要盡可能地少占用土地面積，減少建設成本。為此在選址時要考慮各個超市的貨物銷售速率，超市的銷售情況又與超市覆蓋的人口數、人口密度、消費指數等指標相關。

2.1 權重的確定

權重的大小受到眾多因素影響，建立一個指標體系分析不同因素影響大小至關重要，指標體系的建立應該遵循以下原則:

1)綜合性原則。指標的選擇要考慮配送中心制約的各個指標，盡可能地考慮到各個方面的影響因素。

2)代表性原則。所選指標因子必須具有代表性，從眾多因子中選擇出指標因子應當是能很好地反映超市配送需求的優質因子。

3)實用性原則。建立的指標體系必須是符合我國現階段國情，各個指標因子也應當是在各類統計數據中較易找到的，且對日后生產和生活能產生積極影響。

4)動態性原則。隨著社會和科學技術不斷發展和進步，所選取的指標因子數值也應該是動態發展的［10］，能夠與時俱進，因地制宜，表現出一定的動態性特征，并真實反映影響因素的約束力。

在遵循以上原則基礎上，文中結合配送中心的選址影響因素，建立如圖2所示的指標體系。

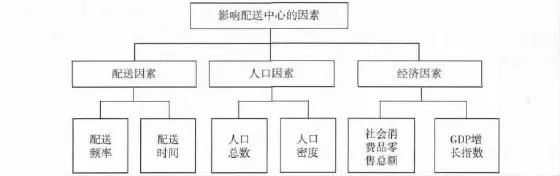
圖2 影響配送中心的因素指標體系示意Fig.2 Schematic diagram of the influence factor system of the distribution center

2.1.1 一級指標權重的確定 一級指標層(配送-人口-經濟)的權重使用主觀賦權G1法［11-12］:

1)專家給予相鄰評價指標xk-1和xk重要性程度指標Rk的理性權重賦值;

2)G1法的權重計算公式

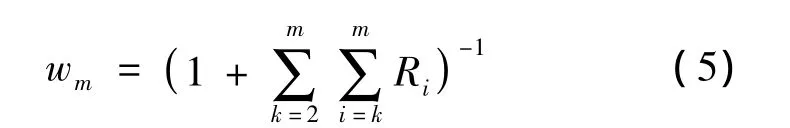
由權重wm可以依次計算得m-1，m-2，3，2個指標權重:wk-1=Rkwk，k=m，m-1，…，3，2。

2.1.2 二級指標權重的確定 二級指標層權重的確定，使用熵值法。

設 xi，j(i=1，2，…，n-1;j=1，2，…，m-1，m)表示第i個系統中第j項指標的觀測數據，對于給定的j，xij的差異越大，該指標對系統的比較作用就越大，即可理解為該項指標所傳輸和包含的信息量越多。熵值法的計算步驟:

1)設ej表示第j個評價指標的熵值，根據熵值計算公式［13］:

其中，ej＞ 0，fij=xij/∑xij為第j個指標下第i個系統的特征比重，xij為第i個系統中的第j項指標的觀測數據(i=1，2，…，n;j=1，2，…，m)。∑xij為第 j項指標的所有系統觀測數據之和;

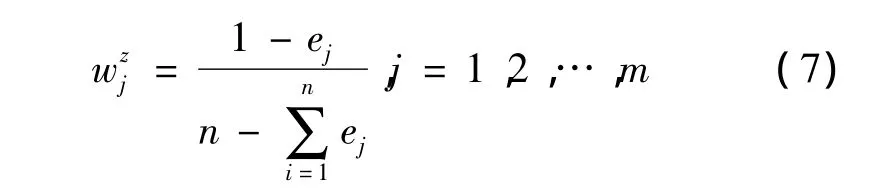
其中，ej為第j個指標的熵值。

熵值法賦權的特點是在所評價的樣本中，同一指標之間的數值差別越大，則權重越大。二級指標權重的確定根據不同地區情況而定。

3 坐標轉換與改進后PGSA算法步驟

3.1 坐標轉換

求解Steiner問題需要使用平面坐標，而在地圖上的坐標為地理坐標，通常為WGS-84坐標，所以存在一個坐標轉化問題。對于坐標轉化問題，文中提供以下兩種方式:

1)軟件轉化法:隨著科技的進步，計算機行業的發展，軟件的功能越發強大和齊全。對于地理坐標和平面坐標的互換已有多款軟件可以完成。COORD就是其中的一款，只需輸入對應的地理坐標選擇需要轉換的坐標即可得到相應的結果，方便準確。

2)公式轉化法:軟件的本質也是集成了公式化的運算，所以在這里也給出了地理坐標的轉化公式。

WGS-84坐標屬于地固坐標系，通常采用WGS-84橢球建立，坐標系的原點是地球質心，Z軸指向BIH1984.0定義的協議地球極CTP方向，X軸指向BIH1984.0零度子午面和CTP赤道的交點，Y軸和Z，X軸構成右手坐標［14］。投影變換方式，見公式(5)，(6)。

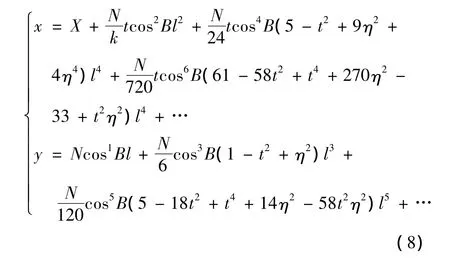
其中，a和b分別表示參考橢球的長短半徑;X為赤道至緯度為B的子午線弧長;卯酉圈曲率半徑:

上述高斯計算公式，是其泰勒級數的展開式，舍去了6次以上高次項，其子午線弧長計算式舍去8次以上高次項。該式縱橫坐標(x，y)的計算精度能夠達到0.001 m。

使用轉換后得到的平面坐標代入改進的模擬植物生長算法求得全局最優解，再將最優解的平面坐標轉換為 WGS-84坐標，以方便工程建設部門使用。

輔助變量:

第二偏心率平方:

3.2 改進后PGSA算法步驟

按照Steiner問題的特點，對人工植物生長的自相似結構做出如下定義:在生長點隨機向各個方向生長并產生新枝，新枝之間旋轉角度 α為90°，分枝長度一般情況下設定為L/1 000(L為有界閉箱長度)。

w1，w2，…，wn表示n個點的綜合權重。求一點p使得minT=∑wi|p-Ai|:

1)確定生長點ai∈X，X為Rn中的有界閉箱，生長點ai為謝爾賓斯基地毯中所有正方形的頂點;

2)求解各生長點的生長概率:

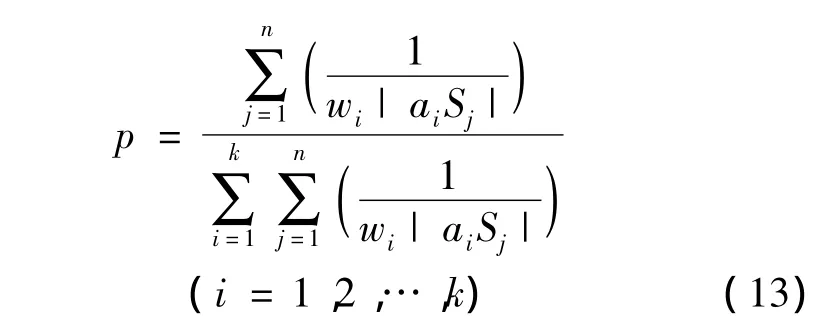
由于目標函數為求最小值，所以計算生長點形態素濃度時取距離之和的倒數(距離之和大的生長點形態素濃度較小);

3)根據2)計算結果建立各生長點在0～1之間的概率空間，以隨機數選擇本次迭代生長點;

4)確定步長(一般為L/1 000，L為有界閉箱);

5)若達到設定的迭代次數后不再產生新的生長點，且得到全局最優解和局部最優解，則停止迭代，否則轉回2)。

4 實證

以無錫市家樂福超市配送中心的選址問題為研究背景。無錫市的家樂福超市共有7家，分布在濱湖、新區、南長、北塘、崇安、錫山6個區。現要考慮設置一個物資配送中心，該點應滿足:

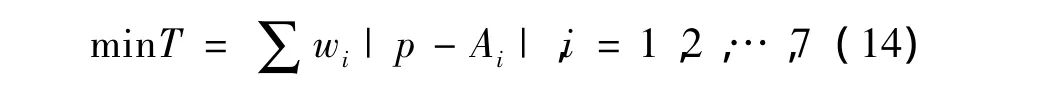
結合無錫市各區的經濟狀況、配送因素、人口因素(一級指標)以及配送頻率、配送時間、人口總數、人口密度、消費指數、GDP增長指數(二級指標)。運用熵值法可以得到指標體系中二級指標的賦權，再結合一級指標賦權，可以得到各指標的最終權重，進而得到各個超市分店的最終權重如表1所示。

通過查詢百度地圖，得到各個區家樂福具體的WGS-84坐標(即經緯度，中央經線設定為120°)，利用坐標轉換公式(5)，(6)將其變換為平面坐標，如表1所示。

將平面坐標數據帶入模擬植物生長算法的程序中，利用Matlab軟件經過5 000步迭代，耗時8 s左右得到全局最優解如表1所示。

圖3所示為百度地圖中各家樂福及配送中具體位置。

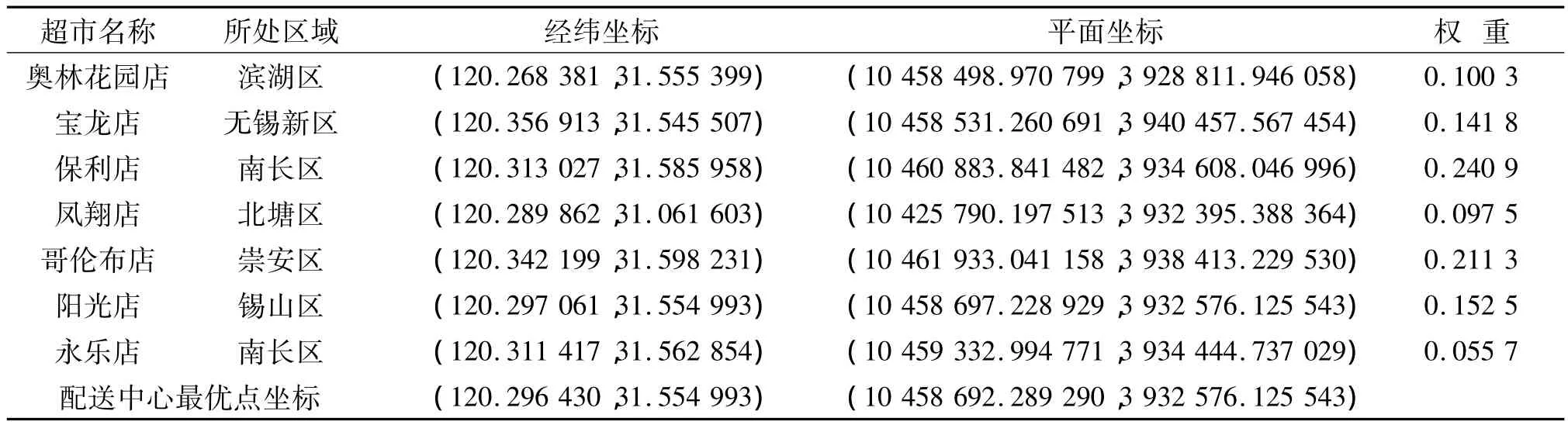
表1 超市坐標和權重Tab.1 Coordinates and weights of the supermarket

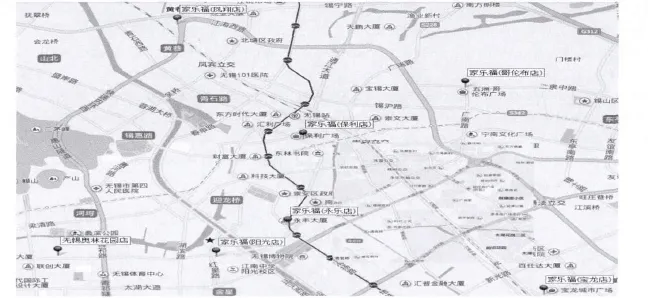
圖3 百度地圖中各家樂福及配送中心具體位置示意Fig.3 Specific location of the Carrefour and distribution center schematic in Baidu map

5 結語

在實際設施選址問題中，會受到多因素的影響和制約。多因素權重合成處理直接影響到最終選址的結果。文中從二級指標體系出發，通過G1法和熵值法確定客戶的權重。

根據PGSA算法的植物向光性概率生長動力機制為啟發式準則，具有較強的全局搜索能力、計算精度高、穩定性好以及應用性強的特點，通過程序計算，得到全局最優解。最后，以無錫市家樂福超市配送中心的選址問題為研究背景進行了實證。

［1］Ali Jamalian，Maziar Salahi.Robust solutions to multi-facility Weber location problem under interval and ellipsoidal uncertainty［J］.Applied Mathematics and Computation，2014(242):179-186.

［2］李磊，謝小璐.韋伯型多點設施優化選址的組合算法研究［J］.計算機工程與應用，2013，49(22):258-261.

LI Lei，XIE Xiaolu.Study on the combination algorithm of location optimization of Webb type multipoint facilities［J］.Computer Engineering and Application，2013，49(22):258-261.(in Chinese)

［3］Harry Venables，Alfredo Moscardini.Ant Colony Optimization and Swarm Intelligence［M］.Brussels，Belgium:Springer，2006.

［4］Lyamine Bouhafs，Amir Hajjam，Abder Koukam.Knowledge based and Intelligent Information and Engineering Systems［M］.Santiago，Chile:Springerlink，2009.

［5］李彤，王春峰，王文波，等.求解整數規劃的一種仿生類全局優化算法—模擬植物生長算法［J］.系統工程理論與實踐，2005，25(1):76-85.

LI Tong，WANG Chunfeng，WANG Wenbo，et al.A global optimization bionics algorithm for solving integer programming-the plant growth simulation algorithm［J］.Systems Engineering Theory and Practice，2005，25(1):76-85.(in Chinese)

［6］李彤，王眾托.模擬植物生長算法在設施選址問題中的應用［J］.系統工程理論與實踐，2008，28(12):107-115.

LI Tong，WANG Zongtuo.Plant growth simulation algorithm of location and its application in facilities［J］.Systems Engineering Theory and Practice，2008，28(12):107-115.(in Chinese)

［7］李彤，陳疇鏞，宿偉玲.求解二層規劃問題的模擬植物生長算法［J］.運籌與管理，2010，10(5):123-128.

LI Tong，CHEN Chóuyong，SU Weiling.Plant simulation for solving two programming problems growth algorithm［J］.Operations Research and Management，2010，10(5):123-128.(in Chinese)

［8］劉學.農村集中供水管理模式與運營問題研究［D］.無錫:江南大學，2012.

［9］遲國泰，祝志川，張玉玲.基于熵權—G1法的科技評價模型及實證研究［J］.科學學研究，2008，26(6):1210-1220.

CHI Guotai，ZHU Zhichuang，ZHANG Yuling.Model of technology evaluation based on entropy weight G1method and empirical study based on［J］.Studies in Science of Science，2008，26(6):1210-1220.(in Chinese)

［10］符林.基于科學發展觀的經濟評價研究及應用［D］.大連:大連理工大學，2008.

［11］郭亞軍.綜合評價理論與方法［M］.北京:科學出版社，2002.

［12］肖翰珅.關于廣義Fermat點唯一性的探討［J］.數學通報，2012，51(10):44-47.

XIAO Hankun.Discussion on the uniqueness of generalized Fermat points［J］.Mathematical Bulletin，2012，51(10):44-47.(in Chinese)

［13］羅德安，廖麗瓊.一種車載GPS系統坐標轉換公式及其應用［J］.西南交通大學學報，2001，36(4):365-368.

LUO Dean，LIAO Liqion.A vehicular GPS coordinate transform formula and its application［J］.Journal of Southwest Jiaotong University，2001，36(4):365-368.(in Chinese)

［14］Mahmood Neshati，Hamid Beigy，Djoerd Hiemstra.Expert group formation using facility location analysis［J］.Information Processing and Management，2014(50):361-383.