夯實“四基” 勿忘傳統

吳之平

在我國，數學教學關注“基本知識與基本能力”的學習與掌握，數學教學“要在堅實的基礎上謀求創新和發展”。“四基”是在我國數學的“雙基”教學的基礎上增加基本思想方法和基本數學活動經驗發展而來的。數學教學中應當把“四基”作為一個整體，貫穿于教學的始終。在進行“四基”教學的時候，如何發揚“雙基”教學的優良傳統，進而達到夯實“四基”的基礎呢？

一、以舊引新，溫故知新

新知往往是舊知的延伸和發展，又是后續知識的基礎。知識的鏈條節節相連、環環相扣、舊里蘊新，又不斷化新為舊，形成知識網絡，學生只有認識到知識之間的聯系，才能深刻理解，融會貫通。以舊引新的方式，能幫助學生復習與即將學習的新知有關的舊知識，從中找到與新知識的聯系點、生長點，順理成章地引出新知，降低新知的難度，提高學習新知的效率。

如教學“有余數除法的驗算”，讓學生計算126÷6和127÷6，復習能整除的驗算方法和有余數的除法，討論：“127÷6，商21是平均分127的嗎？那么平均分了多少？驗算時只用商和除數相乘行嗎？應當怎么辦？”引導學生在掌握整除驗算方法的基礎上，通過比較兩道算式的區別和聯系，理解有余數除法驗算的基本知識，掌握有余數除法驗算的基本技能，既鞏固了能整除的除法驗算方法，又能促進學生對新知（有余數除法驗算方法：被除數=商×除數+余數）的理解和掌握，達到以舊引新、溫故知新的教學效果。

二、記憶助理解，理解促記憶

記憶是理解的基礎，數學教學要強調必要的記憶。如小學生對乘法口訣的記憶與背誦必須成為一種算法上的直覺，看到兩個數字相乘要不假思索就知道結果，速度達到條件反射的程度。但不是所有的數學知識都能符合學生的認知水平，在課堂上學生不能理解的知識要求他們先記憶下來，在練習再中去體驗和理解。如乘法分配律，無論哪種版本的教材都從生活化的事例去引導學生理解，但并不是所有的學生都能用乘法的意義去理解，最后為了讓全體學生學會用新知識去解決問題，有必要引導學生去記憶乘法分配律：兩個數的和與一個數相乘等于和里的每一個加數與這個數相乘，再把積相加。要求學生背誦下來后，再通過練習加強對它理解。

在理解的基礎上記憶，在記憶的基礎上理解。記憶促進理解是傳統“雙基”教學的好傳統，運用得好，對“四基”教學百益而無一害。

三、加強訓練，向速度要效率

國家對小學數學的課時有嚴格的要求，不能擠占其他科目的學習時間，為了加強培養學生的數學素養，數學課只能走提高課堂教學效率的內涵式發展道路。要夯實基礎，使基本運算和基本的思考成為學生的“直覺”，基礎知識達到條件反射的程度，學生才能有足夠的時間去進行更高級的思維活動。在小學數學中口算就是一個最重要的例子，簡單的口算熟練了，有利于學生把注意力集中在更高級的“問題解決”上。

如教學搭配規律，可引導學生填表：

在解題過程中，學生數感會明顯增強，并能下意識地把數和運算的知識運用到觀察、猜測、驗證、發現等活動中，就會順理成章地抽象出：搭配的總次數等于木偶個數與帽子個數乘積的規律。學生的推理思想和抽象的思想得到培養，學生基本歸納的活動經驗、基本抽象的活動經驗得以有效積累。

四、數形結合，提煉數學思想

數學教學中關注數學思想方法的提煉，是中國傳統數學教育的一大特征。華羅庚的數學教育名言中，以“數形結合”一詞流傳最廣大， “數形結合”是一種數學教學方法，更是一種數學思想，數學教師普遍具有數學思想方法的教學意識，力求掌握數學思想方法的內涵，將數學思想方法用于教學預設，并在課堂教學實施，也用于數學解題。

如教學蘇教版“5以內數的認識”，教學目標是：能正確數出5以內物體的個數，會讀、寫1～5各數;學習用操作、畫圖等方法，表示出5以內物體的個數，知道1～5這5個數字的順序;學習用數來描述生活中的物體數量，并逐步養成良好的學習習慣。本課的目標并不難達到。學生已經具有這部分知識（基礎知識）和解決這類知識的方法（基本技能），重點應放在引領學生掌握基本的數學思想和獲取基本的活動經驗。

教學本課時，可先引領學生再次經歷“數出實物的數量（小棒、圓片或手指頭）——用圖表示數量（正方形、三角形、圓形）——用數字表示數量”的抽象過程，幫助學生理解數的意義。在逐步抽象中理解實物、圖形與數字符號之間的關系，滲透數形結合的基本思想，并在正確數數的過程中，建立數感，體會到由物到數的抽象思想和數與實物的對應思想。學生的基本操作、基本合作交流與基本抽象的活動經驗得到進一步提升。

五、熟能生巧，積累基本活動經驗

新課程標準重在關注探究式學習和合作學習，一些專家和學者也是以是否運用這兩種學習方式來衡量一節課的好壞，造成某些教師誤認為只有這兩種學習方式才是好的學習方式，以致盲目地、隨意地運用這兩種學習方式，課堂上教師少講或不講，排斥和否定接受學習方式，導致課堂教學效率低下。其實探究式學習和合作學習只關注了認知過程的前半段，學生探究出新知，并不意味著學習過程的終結，要形成學生的技能，形成學生基本的數學思想和積累學生的數學經驗，還需要鞏固、小結、提升。

傳統的數學教學強調練習，學生經歷了嘗試、探究過程之后，所獲得的知識必須加以鞏固并拓展運用。此外，練習要有一定的強度、速度和深度，但并非簡單的重復，而是依賴變式處理，獲得新意。

例如教學蘇教版四年級下冊的“找規律”，可以設計兩個層次的練習，第一層次是學生解決兩種物體的搭配問題，鞏固新知;第二層次是解決三種物體的搭配問題，進行拓展延伸;第三層次是變式逆向訓練，積累基本活動經驗。

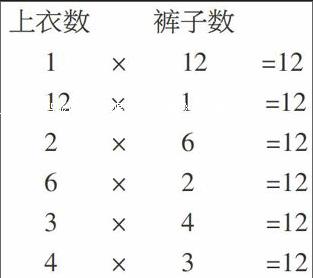
問題：老師為了今天能給同學們留下一個美好的印象，昨晚精心挑選了一些上衣和褲子，共有12種搭配穿法。猜猜看，老師可能有幾件上衣、幾條褲子？

上衣數 褲子數

1 × 12 =12

12 × 1 =12

2 × 6 =12

6 × 2 =12

3 × 4 =12

4 × 3 =12

上面整理出的式子，就是找一個數的約數的方法。通過變式訓練，培養學生創新性思維，積累找約數的經驗。

“對于基本概念的理解要變為直覺。”這是物理學家楊振寧在清華大學給本科生上《基礎物理》時講的一句話，這是對“熟能生巧”的一種現代詮釋，要達到直覺的程度，就要做到無需停頓下來思考。對 “雙基”教學來說，會背基本概念，會做習題是不夠的。數學教育家張奠宙指出：對于方程概念來說，會背“含有未知數的等式叫做方程”是不夠的，必須達到直覺的程度，即知道方程的本質是為尋求未知數，在未知數和已知數之間建立等式關系，當“方程概念”成為直覺后，一旦面對現實問題，立刻就能判斷這是方程問題，而且下意識地在已知數和求知數之間拉上關系，以致成為一種本能。因此，要達到直覺，就需要通過不同層次、不同類型的變式練習，使每個學生通過練習而得到收獲，享受成功。練習多了，時間長了，成功次數多了，興趣濃了，學生的基本數學活動經驗就會豐富。

好的教學改革不是另起爐灶，而是從原有的傳統經驗中揚帆遠航！

（責編 金 鈴）endprint