系統理解百分數 拓展應用百分百

王正義

百分數在生活中應用廣泛，既是學生掌握數概念的重要內容，又是教學中的重、難點。由于百分數是分數的特殊形式，所以百分數應用題的結構與解法和分數應用題是一致的。因此，把百分數應用題的教學納入分數應用題的知識結構中，可以更好地讓學生了解和掌握知識間的內在聯系，擴大、完善自身原有的知識結構。

一、理清概念，細審題

百分數表示兩個數量的倍比關系，不能表示具體的數量（即不能帶單位）。分數則既可以表示一個具體的數量（帶單位），也可以表示兩個數量的倍比關系（不帶單位）。如：“一桶油重10千克，用去■千克，還剩多少千克？”解答后可讓學生討論：（1）把題中的“■千克”換成“■”，題意變了沒有？是否可以這樣變換？（2）把題中的“■千克”換成“20%千克”，題意是否相同？可否這樣？（3）把題中的“■千克”換成“20%”，與第一次改題是否相同？通過討論，讓學生明白審題的重要性，從而養成認真審題的良好習慣。

首先，注重理解和區別“多（少）幾”與“多（少）百分之幾（幾分之幾）”的含義。（1）“多多少”與“少多少”的意義是比差，應直接求兩個數的差，如“8千克比5千克多多少”“5千克比8千克少多少”等。（2）“多或少百分之幾（幾分之幾）”的意義是比倍，應該用兩個數的差除以標準數（單位“1”），如“8千克比5千克多百分之幾（幾分之幾）”“5千克比8千克少百分之幾（幾分之幾）”等。

其次，認真區別處理三類情況。（1）不名數與幾分之幾（或小數）可直接相加減，如“15加上■，等于多少”“15加上0.2，等于多少”等。（2）如“15增加了20%，等于多少”“15加上它的■，等于多少”等問題中的分數、百分數是倍比關系，而不是實際數值，應加上（或減去）這個數的百分之幾或幾分之幾。（3）名數與名數可直接相加減，如“比0.6千克多■千克是多少”“0.6千克加上■千克，等于多少”等。

再次，弄清題意，找準應用題中的單位“1”。（1）一般情況下，在“比”“是”“占”或“相當于”等字眼后面的“誰”，就是單位“1”。（2）同誰比，誰就是單位“1”。（3）求誰的幾分之幾（百分之幾），誰就是單位“1”。

二、區分類型，夯基礎

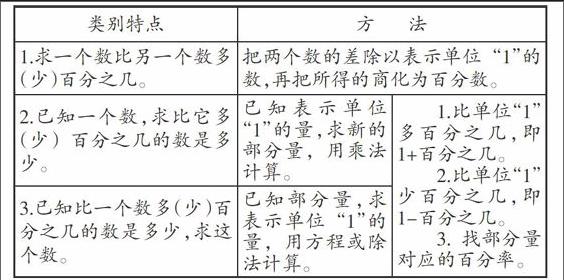
教師應注重應用題教學，引導學生從例題中理解數量關系，并把學生的理解引向深入，使學生正確掌握解答百分數應用題的基本方法。可列表如下：

■

三、發展引申，重比較

課堂教學中，教師應將兩種容易混淆的概念，或者將相似（或相同）的數量關系放在一起，讓學生進行比較，并引導他們充分發揮舊知識的正遷移作用，克服“多（少）幾”對“多（少）百分之幾”的干擾。對稍復雜的應用題，教師要鼓勵學生先從總體上觀察，全面感知題意，再引導他們對題中的數量進行分析，從而掌握解題思路和解題關鍵，提高解題的能力。這樣由三類基本題通過發展變式得到三類相應的引申題，教師可通過列表加以比較，揭示它們的本質聯系和區別，使學生真正掌握所學知識。如下：

■

四、靈活思維，促拓展

學生解題的直覺經驗來自于對數量關系的理解與概括，正是這種深刻的理解與概括，使學生形成“動力定型”，并順利遷移到解決稍復雜應用題之中，能動地運用數量關系解決問題。例如，蘇教版小學數學六年級上冊第106頁例5求出勤率，這是百分率在生產生活中的具體應用，讓學生理解“率”是兩個數相除所得的倍比關系，沒有單位名稱，表示實際出勤人數占應出勤人數的百分之幾，提醒學生注意出勤率、發芽率、出油率、成活率、合格率等都不大于單位“1”（100%）。經過訓練后可出示一些選擇題給學生練習，培養學生的發散性思維。如：“學校田徑隊周二出勤38人，缺勤2人，周二的出勤率是（ ）。”

①■×100℅ ②■×100℅

③■×100℅ ④■×100℅

又如，蘇教版小學數學六年級下冊第17頁的一道思考題：“一件商品，按成本價提高30%后出售。后來因為季節原因，又打八折出售，降價后每件商品賣104元。這種商品賣出一件是賠還是賺？賠或賺多少元？”學生通過分析找到數量的對應分率，確定解題思路，然后用方程x×（1+30%）×80%=104或算術方法104÷80%÷（1+30%）求出成本價，再把成本價與現價相比較，從而解決問題。

此外，在百分數應用題教學中，教師還應注重通過潛移默化的啟發、誘導，使學生從定量分析逐步轉化為變量分析，從而拓展學生思維的深度和廣度。特別是在復習階段，教師更要充分發揮“一題三變”的思維訓練作用，使學生內化所學知識。

一是一題多問。通過對相同數量的多問多思，有效培養學生思維的廣闊性和靈活性，提高他們對數量關系的理解能力，并順利遷移到解答復合應用題的過程中，重新變通數量關系，獲得多解。如：“金湖實小合唱隊有80人，鼓號隊有100人。（1）合唱隊人數是鼓號隊人數的百分之幾？（2）鼓號隊人數是合唱隊人數的百分之幾？（3）合唱隊人數占兩隊總人數的百分之幾？（4）鼓號隊人數占兩隊總人數的百分之幾？（5）合唱隊人數比鼓號隊人數少百分之幾？（6）鼓號隊人數比合唱隊人數多百分之幾？”

二是一題多解。教師可鼓勵學生突破單一思維，從多方面思考問題，從不同角度解答問題。一些學生之所以對應用題望而生畏，究其原因在于他們不善于揭示題中隱藏的各種數量關系，也不善于從多角度去分析這些數量關系。因此，教師應該積極引導，善于喚起學生有關知識和解題經驗的再現，誘發學生根據數量關系發散思維，實現各種思路的溝通。如：“金湖實小美術組有40人，書法組人數占美術組人數的80%，書法組和美術組共有多少人？”用百分數方法解，列式為40×（1+80%）;用歸一問題方法解，列式為40÷5×4+40或40÷100×80+40;用方程解，列式為x-40×80%=40……

三是一題多變。在揭示一些典型題目的數量關系時，教師要善于設計變式題，變化非本質特性，突出本質特性，讓學生在變中求通，加深對應用題解題思路的理解。如：“（1）修路隊修一條20千米長的公路，已修了20%（或■），已修了多少千米？（2）修路隊修一條20千米長的公路，已修了20%（或■），還剩多少千米沒修？（3）修路隊修一條20千米長的公路，已修了■千米，已修了幾分之幾？（4）修路隊修一條公路，已修了■千米，還剩20千米，這條公路共有多少千米？（5）修路隊修一條公路，已修了■，正好是20千米，這條公路共有多少千米？（6）修路隊修一條公路，已修了■，還剩20千米，這條公路共有多少千米？”

總之，課堂教學中，教師要引導學生梳理百分數的知識，使學生真正內化所學知識，完善自身的知識結構，從而獲得發展。

（責編 藍 天）endprint