探索規(guī)律，發(fā)展解決問題能力

朱輝

探索生活現(xiàn)象或數(shù)學現(xiàn)象中蘊含的規(guī)律，是數(shù)學學習的重要使命之一。因此，教學中要善于引導學生經歷發(fā)現(xiàn)規(guī)律的過程，促進學生理解部分與整體的內在聯(lián)系，通過有限去感悟無限，實現(xiàn)問題的有效解決。

一、聯(lián)系生活，感知規(guī)律

探索規(guī)律是學生挑戰(zhàn)自我的表現(xiàn)，也是展示學生才華與智慧的重要窗口。這是一個充滿情趣與驚喜的探索之旅，學生能充分激活自己的知識積累、經驗儲備，進而積極地探索。探索數(shù)學現(xiàn)象中的規(guī)律，其間有困惑，也有喜悅，這是矛盾的載體，它會抓住學生的獵奇心理，誘發(fā)學生探究的好奇心，促使他們積極思考、樂于思考、敢于嘗試。

如，在四年級上冊“找規(guī)律”教學中，就以學生非常熟悉的情境為教學切入點：今天是星期幾？明天呢？……通過司空見慣、極其熟悉的現(xiàn)象拉近規(guī)律與學生的距離，讓學生感知到生活有規(guī)律，要善于研究和發(fā)現(xiàn)它們。利用學生的生活味原型，讓學生在審視現(xiàn)實生活的同時，自發(fā)地感悟其中蘊藏的數(shù)學現(xiàn)象，從而激發(fā)學生學習數(shù)學的興趣，使學生感受到數(shù)學與生活的密切聯(lián)系。

再如，觀察排列“□★○△□★○△…”，猜想其中蘊含的規(guī)律，想一想第9個是（ ? ? ?）。學生把圖形的規(guī)律弄清楚了，就很容易確定下一組圖形。利用具體的圖像提供的豐富表象，學生能夠感知規(guī)律，并以規(guī)律作為判斷的依據(jù)，順利突破思維瓶頸，迅速解決問題。

二、活動反思，探究規(guī)律

巧妙地組織活動，引導學生對活動進行反思，探究規(guī)律，發(fā)現(xiàn)周期，利用周期的確定性去探求解決的方法。

如，在“找規(guī)律”的教學中，首先，設計站隊活動游戲，讓學生按照“男生、女生、男生……”這一規(guī)律排成一列;其次，利用人數(shù)增減的活動，引發(fā)學生思考“在變化中你發(fā)現(xiàn)了什么？”由于活動的主體是學生，學生會在站隊中發(fā)現(xiàn)這種周而復始的規(guī)律。同時，在不同形式的變化中學生能夠清晰地發(fā)現(xiàn)“開始男生，最后也是男生，男生一定比女生多1個”的規(guī)律，從而非常輕松地突破問題的難點。

再次，引入教材的主題圖，引領學生進行觀察，學生會自覺地把圖中的信息進行梳理，也很直觀地感悟到：夾子與手帕的關系、兔子與蘑菇的聯(lián)系、籬笆與樁的關聯(lián)性……圖中的規(guī)律和站隊活動的規(guī)律有機融合，實現(xiàn)學習的整合，促進知識的提煉和升華，學生能看出物與物之間的內在聯(lián)系，悟出其中的周期性，從而能極其準確地把握規(guī)律。

三、靈活思索，發(fā)現(xiàn)規(guī)律

盡管生活現(xiàn)象、數(shù)學現(xiàn)象都紛繁復雜，但其中蘊含的規(guī)律是井然有序的。因此教師要促進學生從不同的角度去探索規(guī)律所在，讓學生能夠掌握其中的周期性，并進行科學合規(guī)的推理。例如，在具體的教學時組織畫一畫、想一想、算一算等自主學習活動，促使隱藏在現(xiàn)象中的規(guī)律逐步凸顯出來，進而再現(xiàn)周期規(guī)律的合情推理活動。

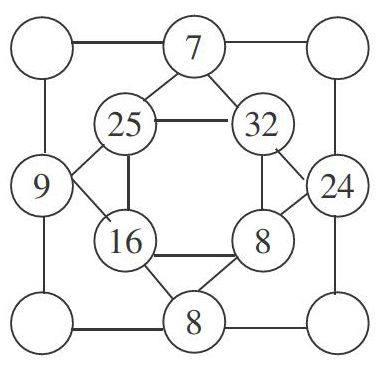
再如，在“教學100以內的加、減法”之后，組織競賽游戲。先指導學生在最里面的小正方形的4個角中，任意地寫出4個數(shù);再組織學生計算出相鄰兩個數(shù)的差（大數(shù)減小數(shù)），并填在外圍的正方形中;接著讓學生自主探索規(guī)律……活動不僅能激發(fā)學生的探究興趣，也讓學生學會有序思考。當學生按照規(guī)律進行不斷拓展時，他們一定會發(fā)現(xiàn)：最外邊的正方形，四個角上的數(shù)最終都會變成0。

自主探索、小組合作，讓發(fā)現(xiàn)規(guī)律變得簡單輕松。學生在認真計算、分析后發(fā)現(xiàn)規(guī)律是那么的真實，從而充滿了成就感。

四、內化知識，應用規(guī)律

探索規(guī)律的最終目的是應用知識，讓其內化，達成學以致用的理想境界。所以在教學中教師不僅要努力創(chuàng)設適宜的情境，激活學生的認知積累，引領學生進行必要的探索研究活動，還要引導學生進行科學的歸納，使規(guī)律與數(shù)學知識學習更加緊密地結合，從而促進學生對新知的建構。

如，在“分數(shù)的基本性質”教學中，設計思考題 “一個分數(shù)的分子和分母都加上同一個數(shù)，這個新分數(shù)與原來的分數(shù)相比較，你認為符合分數(shù)的基本性質嗎？為什么？”學生會舉出不同的實例來驗證該說法的不科學性，有的學生會在特殊的舉例中獲得結論：如果這個分數(shù)是等于1的假分數(shù)，那么這個規(guī)律是可以用的。學生的不同例證有效地拓寬了學習視角，學生會在分析研究中逐步明白，分數(shù)的基本性質只適用于分子和分母的倍數(shù)關系，而不適用于和差關系。同時，還可以引導學生去探究特例“2 / 3的分子加10，分母加上幾，分數(shù)的大小不變？”使數(shù)學學習更具靈活性。

悟規(guī)律、找規(guī)律是探究學習的理想追求，教師要在這個過程促進學生通過歸納、類比獲得猜想，進而推動學生加深對數(shù)學知識的理解進程，提升思考的層次。

（責編 童 夏）