城市住房價格局部線性地理加權回歸分析——以湖北省黃石市為例

王新剛， 孔云峰

（河南大學環境與規劃學院，河南 開封 475001）

城市住房價格局部線性地理加權回歸分析
——以湖北省黃石市為例

王新剛， 孔云峰

（河南大學環境與規劃學院，河南 開封 475001）

研究目的：以土地稀缺、資源組團型城市——湖北省黃石市為例，嘗試引入局部線性地理加權回歸（LLGWR）方法，探索住房價格及影響因子的空間變化規律，為政府房地產市場管理和土地利用規劃提供借鑒。研究方法：整理1.93×104個住房樣本和398個樓棟樣本，遴選樓棟總層數、容積率、綠化率、小區等級、距區域中心距離、銷售年份等作為解釋變量，采用LLGWR方法構建城市住房價格的模型，并進行分析與解釋。研究結果：與常規線性回歸（OLS）相比，地理加權回歸（GWR）和LLGWR能更合理和準確地解釋住房價格的空間變異，且LLGWR優于GWR；銷售年份、容積率、地理區位能顯著影響住房價格，同時樓棟總層數、綠化率等因素影響住房價格，且在不同功能片區具有明顯差異。研究結論：LLGWR模型可以實現系數函數和誤差方差的無偏估計，提高模型的估測精度，能更為準確地解釋住房價格；宏觀市場趨勢是影響住房價格的關鍵因素，但在不同的地理區位，住房價格增長趨勢有明顯的差異；土地利用規劃和土地供應影響房地產空間分布，但研究區內土地價格對住房價格的影響不明顯。

不動產價格；住房價格；局部線性地理加權回歸（LLGWR）；黃石市

1 引言

住房作為不動產，其價格是社會關注度最高的熱點問題之一。分析和預測住房價格的空間分布和變化趨勢是居民、投資者、開發商以及政府管理部門關注的重要問題[1]。住房價格與住房特征要素相關，與市場供給和社會消費水平相關，也受到國家和地方土地供應等政策因素影響[2-3]。土地要素作為城市房地產的重要構成部分，與住房價格具有密切的聯系[4]。土地供應能夠影響市場預期而引起房價的變化[5]；住宅價格與土地價格相互影響，互為因果[6]。

而從地理空間的角度，土地利用和城市規劃引起城市居住空間結構向多核、分散組團發展[7-8]，區位是影響住房價格的一個關鍵因素。因住房價格在空間鄰域上的相關性和異質性，在統計上具有非平穩性，通常采用地理加權回歸（GWR）模型進行區位分析[9]。通過對價格和相關的影響因素進行回歸統計，探測區位因素對價格的影響機制[10-12]。

然而，GWR本質上屬于Nadaraya-Watson核估計統計方法，存在邊界效應[13]。模型的回歸系數是空間地理位置的函數，與一維區間相比，邊界效應更為劇烈，使得邊界區域的估計容易失真，從而導致分析結果偏離實際情況。Wang等[14]提出局部線性地理加權回歸（LLGWR）方法，較好的解決了邊界效應問題。目前該模型僅在數學領域進行了理論證明，尚未有實證分析的文獻報道。本文嘗試將LLGWR方法引入城市住房價格空間分析，以土地稀缺、典型組團型城市——湖北省黃石市為例，探索并解釋城市住房價格及影響因子的空間變化規律，為政府部門管理房地產市場，做好土地開發和利用提供科學參考。

2 LLGWR方法的概念

GWR是建立在空間相關性和空間異質性假設前提下的局部回歸分析，具有概念上的簡單性和實現上的易操作性。設Y為因變量， X1，X2，…，Xm為自變量，（Yi；X1，X2，…，Xm）表示因變量和自變量在地理位置（ui，vi）處的觀測值（i=1，2，…，n ），GWR模型基本公式為：

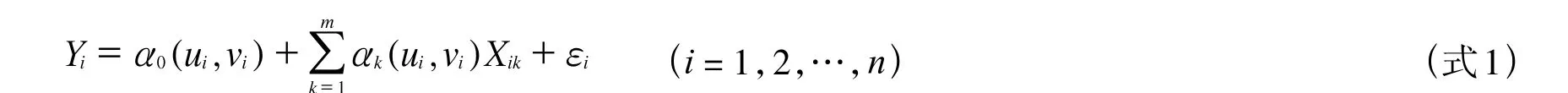
式1中，回歸系數αk（u, v）（k=0，1，2，…，m）是地理坐標（u，v）的函數。殘差εi（i=1，2，…，n）為獨立同分布的誤差項，服從正態分布且E（εi）=0，Var（εi）=σ2。

采用局部線性擬合方法，將系數函數局部展開為地理坐標的線性函數，可將GWR模型擴展為局部線性GWR模型（LLGWR）。

記Xi=（Xi1，Xi2，…，Xim）T是自變量的第i組觀測值構成的列向量，X=（X1，X2，…，Xn）為因變量矩陣。在給定區域內任一點（ui，vi），設wi（ui，vi）為（ui，vi）點的第i個權重值，wi（ui，vi）=Diag（w1（ui，vi）, w2（ui，vi），…，wn（ui，vi））表示點（ui，vi）的空間權重矩陣。

令：X（ui，vi）=

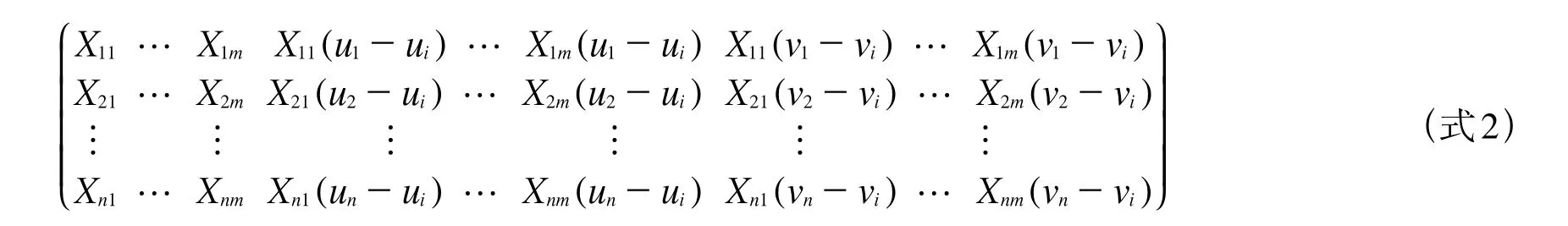
則帽子矩陣為：

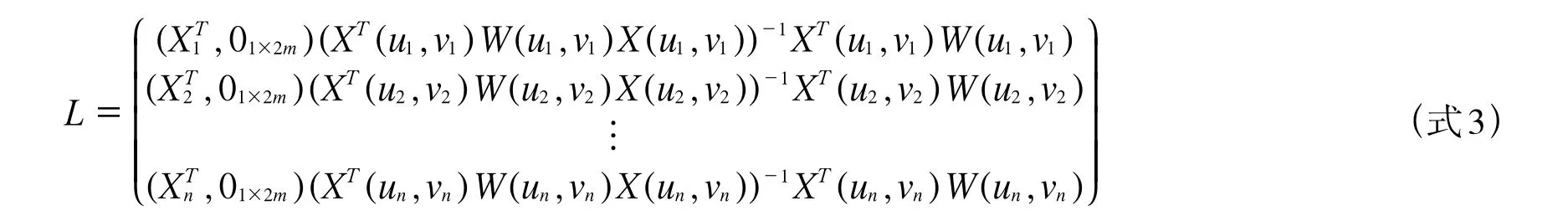
因變量Yi=（Y1，Y2，…，Yn）T在n個觀測點處的擬合值為：

與GWR模型一樣，空間權重矩陣W（ui，vi）表示對于地理位置（ui，vi），（uj，vj）參數估計的重要性，（uj，vj）與地理位置（ui，vi）越近，權重越大。有兩種常見的方法構建空間權重矩陣：固定核和自適應核。對于固定核，距離是固定的，而鄰近樣本的數量是變化的。對于自適應核，距離是變化的，而鄰近樣本的數量是固定的[9]。

通常采用高斯距離衰減函數確定空間權重，如式5。式5中wij表示點（uj，vj）和點（ui，vi）之間的權重，dij表示點（uj，vj）到點（ui，vi）的歐氏距離，h是帶寬參數。 固定核的帶寬h是在均值與方差之間平衡的一個參數，如果h值過大，就趨向于全局模型；如果h值太小，系數估計的方差很大。

若空間數據分布不均勻，為避免數據稀疏的區域擴大空間的異質性或數據密集的區域掩蓋了敏感的空間異質性[9]，自適應核能夠根據數據分布情況，選取數量相同的最鄰近點，自適應調整帶寬，從而在數據點密集的地方減小帶寬，在數據點稀疏的地方增加帶寬。例如，bi-square權重函數如式6。式6中hi表示第i個觀測點（ui，vi）的帶寬。

回歸系數的估計依賴于帶寬參數h的選擇，最優帶寬參數可根據AICc準則確定[15]，如式7。此處，σ?是隨機誤差項的極大似然估計，設SSE表示殘差的平方和，近似的取σ?2=SSE/( n -tr( L))，t（rL）是帽子矩陣L的跡。當AICc值最小時，相應的h即是最佳的帶寬。

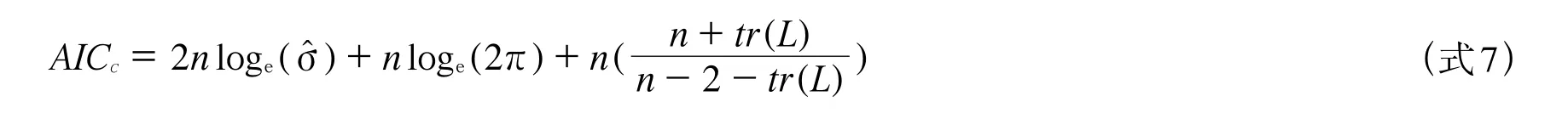
局部線性回歸（LLGWR）方法在廣泛的系數函數類型下，可以得到系數函數和誤差方差的無偏估計[16]，因而改進了GWR方法，能夠提高模型估計精度。

3 研究區域及樣本數據

黃石市位于湖北省東南部，長江中游南岸，是武漢城市圈副中心城市，中國中部地區重要的原材料工業基地。全市下轄黃石港區、西塞山區、下陸區、鐵山區及團城山經濟技術開發區（圖1），市區面積226 km2，人口78×104人。黃石市是典型的資源組團型城市，地形較為復雜、土地稀缺，具有區域分散、多中心的空間結構特點；依據地形條件、傳統產業布局和近年土地規劃，城區發展采用中心組團式布局：鐵山區、下陸區和西塞山區為工礦區；黃石港區南部為商業中心區，北部為花湖物流中心區；團城山區北部沿湖為行政中心區，山南為經濟技術開發區。受城市和土地利用規劃影響，該市房地產市場主要集中分布在黃石港區和團城山區。

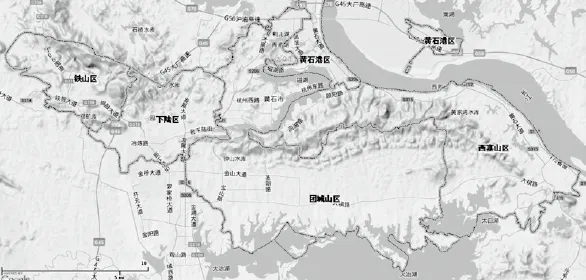
圖1 研究區地形圖Fig.1 The topographic map of study area

本文數據來源于黃石市房地產局新建商品房網簽備案系統。選擇2007—2012年的商品住宅成交價格數據1.93萬個（鐵山區無數據）。為便于作整體分析，按樓棟計算平均住房單價，共獲得398個樓棟樣本點。依據黃石市城區綜合用地級別圖（2008年）并結合城市規劃，將研究區劃分為4個區域：黃石港區南部商業區、黃石港區北部花湖物流區、團城山開發區、下陸區老工業區，選擇各區域中土地級別最高的地塊中心為區域中心點。

針對樣本數據進行相關分析，發現價格與主要銷售年份、樓棟總層數、容積率、小區等級、綠化率呈現或強或弱的線性相關關系；而研究區土地成交價影響住房價格變化的相關性很弱，原因可能在于開發商從獲得土地到樓盤銷售的周期較長，也有部分開發商有意囤積土地。運用探索性空間數據分析，住房價格的Moran's I為0.19，具有較強的空間正自相關性；聚類和異常值分析（Anselin Local Moran's I），表明住房價格具有局部空間異質性；住房所在區域和區位對價格影響顯著。

選擇價格解釋變量：反映土地稀缺和建筑成本的容積率（PR）和樓棟總層數（FL），反映社區環境的小區等級（CL）和綠化率（GR），反映城市區位屬性的住房距區域中心距離（ND），以及反映宏觀經濟和土地供應等政策變化的銷售年份（YI）。

4 回歸分析

運用常規線性回歸（OLS）方法進行全局模型估計。模型擬合度R2=0.49，能合理解釋49%的住房價格變化原因。模型的F檢驗值為75.88，其相應的概率為0.00＜0.05，表明通過顯著性水平為0.05的F檢驗；除距區域中心距離外，各回歸系數t檢驗值均大于3，各回歸系數的置信水平均為95%以上，表明各回歸系數與住房價格的線性關系顯著。同時，計算各自變量的方差膨脹因子進行檢驗[17]，發現自變量VIF值均小于2，遠小于10，表明變量間的多重共線性現象較弱，適合于OLS模型分析。

回歸結果也表明：黃石市住房價格可以由住房的本身屬性、環境因素、區位屬性和時間因素來建模；住房價格與容積率、銷售年份、樓棟總層數、小區等級、綠化率成正相關關系，而與住房距區域中心距離成負相關關系；小區等級和銷售年份與住房價格有著同方向的緊密聯系；非常特殊的是，與其他城市不同，研究區內土地稀缺，開發強度較大，容積率越高，住房價格反而越高。不過，OLS模型只是提供全局平均意義上的一定程度上的解釋，尚有51%的住房價格的變化未能解釋，部分原因在于全局模型是假設在空間內住房價格的持續變化是平穩的，而實際上其變化具有非平穩性[9]。

研究區住房均價分析表明，在樣本區域住房的分布是不均勻的：在靠近4個中心區域密度大，向外圍區域密度低；住房均價的空間分布也是非均質的，即具有空間的異質性：在4個區域，靠近中心位置的住房均價普遍高于外圍區域。樣本數據特征表明，地理加權回歸分析適合于全市住房價格分析。由于空間的異質性，變量之間的關系是隨空間位置的變化而變化的，OLS模型并未考慮這種變化特征，進一步利用GWR模型進行局部統計分析。

因樣本數據空間分布的非均質性，采用bi-square自適應核函數，避免了某些樣本點的鄰近樣本數據稀疏而造成的估計偏差[9]。GWR模型估計結果如表1，模型的擬合度R2為0.82，與OLS模型的擬合度相比，有大幅度的提高，說明模型描述的回歸關系具有空間非平穩性；AICc值作為模型擬合顯著性的標識，由OLS模型的6388下降到GWR模型的6262，減少了126，遠大于3[9]，表明GWR模型改進回歸的擬合度是十分顯著的，即使增加了計算復雜性，GWR模型也優于OLS模型。同時，GWR模型的統計檢驗F值為1.44，相應概率P值為0.00＜0.05，小于給定的顯著性水平0.05，GWR模型擬合黃石市的住房均價，明顯優于OLS模型，住房均價與影響因素之間的整體關系確實存在顯著的空間非平穩性。

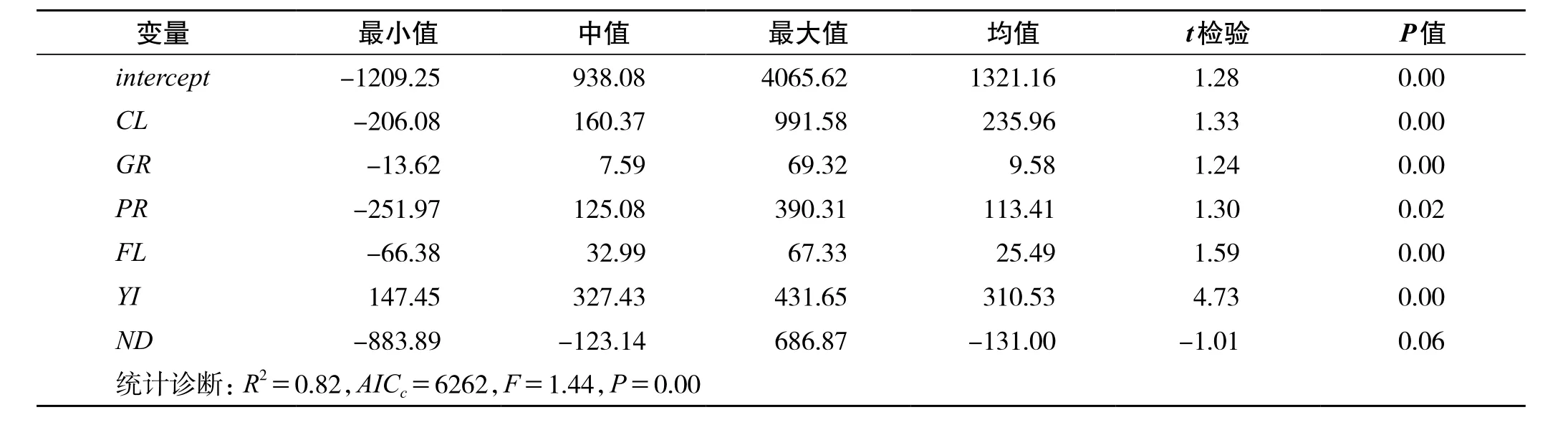
表1 GWR模型回歸系數的估計結果Tab.1 The estimation results of GWR regression coeffcient

考慮到研究區域地形特殊，山體和湖泊眾多，4個區域空間邊界復雜，進一步利用LLGWR模型進行局部統計分析。采用三階距χ2逼近方法計算，檢驗LLGWR各回歸系數變化的顯著性[18]。模型估計結果如表2，檢驗統計量F值為3.22，與之相應的顯著性檢驗概率P為0.00＜0.05，模型通過顯著性水平為0.05的F檢驗。各回歸系數t檢驗的顯著性概率P值為0.05，通過顯著性水平為0.05的t檢驗，表明各回歸系數隨空間位置的變化具有顯著性。同時，與GWR相比，LLGWR方法將AICc值減小34；擬合度R2由0.82提高到0.87；F統計值由1.44提高到3.22；這些表明LLGWR優于GWR。

5 LLGWR結果分析

LLGWR回歸系數反映了各解釋變量的空間變異狀況。因所有系數均接近正態分布，將系數標準化，并按0.5的間隔進行分類，在GIS軟件中制作系數空間分布示意圖。

研究區土地規劃具有多中心的空間結構特點，城市區位是影響住房價格的重要因素。距區域中心距離的遠近一定程度上反映了住房用地級別的不同，與住房價格具顯著的負相關性（圖2）。樓棟到區域中心距離每增加1 km，住房價格平均減少74.18元/m2。當然，同一小區樓棟到區域中心距離相差較小，住房價格受此影響較小，圖3中差異不明顯；而不同小區樓棟受距區域中心距離的影響較大。

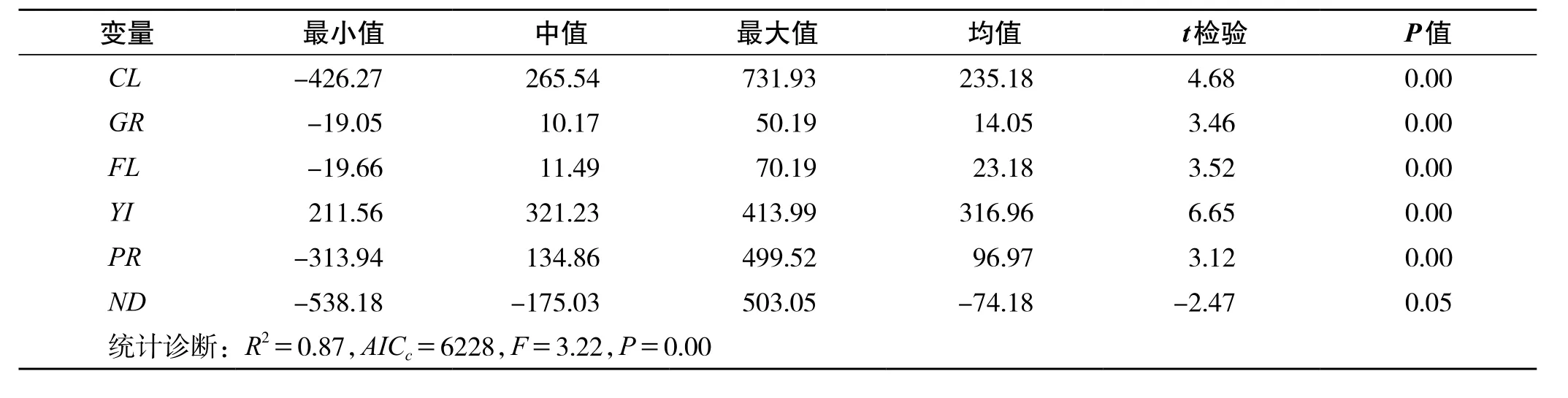
表2 LLGWR模型回歸系數的估計結果Tab.2 The estimation results of LLGWR regression coeffcient

受宏觀經濟趨勢和土地供應等政策變化影響，銷售年份是影響研究區住房價格的重要時間因素，兩者之間具有較強的正相關性。時間每遞增1年，住房價格平均增加316.96元/m2。同時，銷售年份對住房價格的影響具有空間非一致性（圖3）。在西塞山區和黃石港區靠近湖邊和江邊位置，住房價格上升幅度大。原因在于近兩年黃石市江灘和磁湖治理具有成效，使靠近江邊和湖邊的樓盤環境得到改善，價格增幅比較顯著。

小區等級代表小區的檔次定位，與小區規模、樓盤品質、配套服務設施等相關，與住房價格之間具有正相關性。小區等級數每上升1，住房價格平均升高235.18元/m2。小區等級對住房價格的影響具有顯著的空間非一致性（圖4）：在商業或行政中心核心片區，小區等級對住房價格影響較小；在城市中心的外圍片區，對住房價格影響比較大。原因在于城市中心區區位優勢是影響住房價格的主要因素，而在外圍地區，住房要依靠住宅小區品質和檔次提升價格。

綠化率是居住區用地范圍內各類綠地的總和與居住區用地的比率，其高低在一定程度上反映居住環境的質量，也是影響住房價格的因素之一。綠化率提高1%，住房價格平均提高14.05元/m2。綠化率對住房價格影響分布見圖5，回歸系數的估計值在空間上呈明顯的變化。靠近市中心位置，綠化率對住房價格影響很小；在離市中心較遠位置，其對住房價格有較大影響。在局部片區，其對住房價格影響十分顯著，如黃石港區華新水泥廠和黃石火電廠、西塞山區作為工礦區對環境有負面影響，從而造成住房價格隨綠化率的變化而有明顯的變化。

樓棟總層數與住房價格具有一定的正相關性。樓棟每增加1層，住房價格平均增加23.18元/m2。黃石市的住房用地供應緊張，高層住宅或超高層住宅是發展的方向；而樓棟總層數增加，也意味著住房建筑成本的增加，其回歸系數估計值在空間上顯著變化（圖6）。在距離市中心較遠位置，樓棟總層數對住房價格的影響比較顯著；而在靠近市中心位置，影響比較小，其原因估計是靠近市中心位置，樓棟總層數普遍都比較高，而偏離市區位置，高層住宅較少，其成本對住房價格影響比較明顯。

通常來說，隨建筑容積率增加住房價格降低。但在黃石市，容積率與住房價格整體上呈現正相關性，容積率增加1.0，住房價格平均增加96.97元/m2。原因可能是土地資源緊缺，多數住宅設計為高層建筑，在提高容積率的同時建筑成本增加。同時，容積率回歸系數在不同片區差異顯著（圖7）：距離市中心較近片區，容積率對價格影響小，偏遠位置尤其是團城山開發區、花湖新區，容積率顯著的影響住房價格，其原因是偏遠位置小區，建設高層住宅提高容積率，造成房屋成本增加，促使住房價格有明顯的升高。

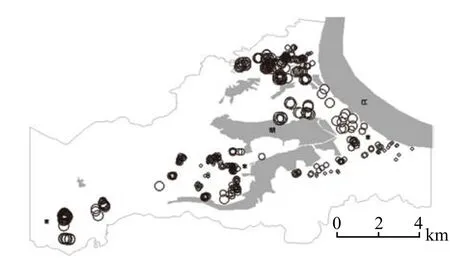
圖2 距區域中心距離系數估計值的分布圖Fig.2 The distribution map of coeffcient estimates on distance from the regional centre

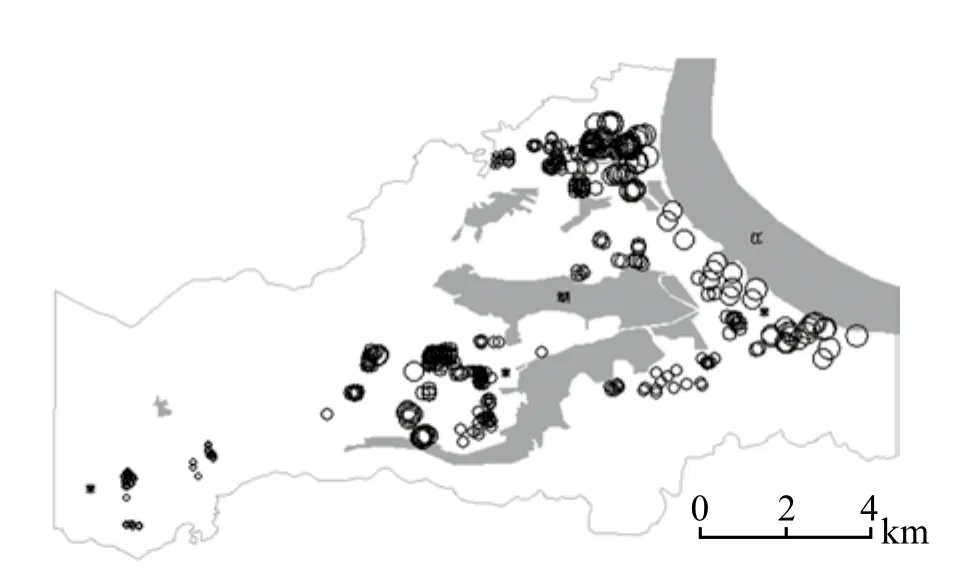
圖3 銷售年份系數估計值的分布圖Fig.3 The distribution map of coeffcient estimates on sales year

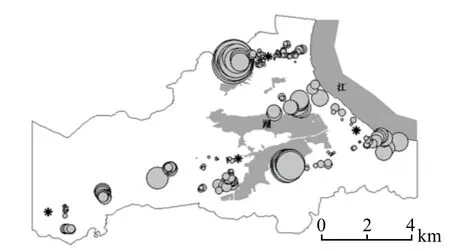
圖4 小區等級系數估計值的分布圖Fig.4 The distribution map of coeffcient estimates on cell level

圖5 綠化率系數估計值的分布圖Fig.5 The distribution map of coeffcient estimates on greening rate

圖6 樓棟總層數系數估計值的分布圖Fig.6 The distribution map of coeffcient estimates on foors

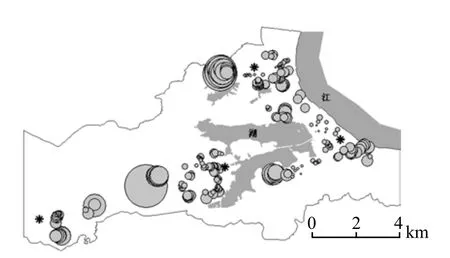
圖7 小區容積率系數估計值的分布圖Fig.7 The distribution map of coeffcient estimates on cell plot ratio

6 結論

本文以典型的土地稀缺、資源組團型城市——湖北省黃石市為例，結合其多個片區中心、地形復雜的特點，構建城市住房價格的局部線性地理加權回歸（LLGWR）模型，探索了住房價格及影響因子的空間變化規律。案例分析發現：（1）與常規線性回歸（OLS）相比，GWR和LLGWR模型采用局部光滑擬合方法，考慮了住房價格的空間異質性，能更為準確地解釋住房價格，且LLGWR優于GWR；（2）宏觀市場趨勢是影響住房價格的關鍵因素，但在不同的地理區位，住房價格增長趨勢有明顯的差異；（3）反映土地緊缺的容積率與住房價格具有顯著的正相關性，但在不同的功能片區，其影響力具有差異；（4）研究區土地規劃具有多中心的空間結構特征，城市區位是影響住房價格的重要因素，兩者具有較顯著的相關性，在商業中心區和行政中心區，價格受區位影響最為突出；（5）研究區土地供應等政策變化影響房地產空間分布，但土地價格與住房價格之間并無明顯的相關關系。

（

）：

［1］ Adair A.S., Berry J.N., McGreal W.S. Hedonic modeling,housing submarkets and residential valuation［J］ . Journal of Property Research, 1996, 13（1）: 67 - 83.

［2］ 阮連法，包洪潔，溫海珍.重大事件對城市住宅價格的影響來自杭州市的證據［J］ . 中國土地科學，2012，26（12）：41 - 47.

［3］ 王松濤，劉洪玉.土地供應政策對住房供給與住房價格的影響研究［J］ . 土木工程學報，2009，42（10）：116 - 121.

［4］ Pollakowski H.O.,Wachter S.M. The effects of land-use constraints on housing prices ［J］ . Land Eco-nomics, 1990, 66（3）: 315 - 324.

［5］ 黃忠華，虞曉芬，杜雪君.土地供應對住房價格影響的實證研究——以上海市為例［J］ . 經濟地理，2009，29（4）：624 - 627.

［6］ 張娟峰.住宅價格與土地價格的城市間差異及其決定因素研究［D］ . 杭州：浙江大學，2008.

［7］ 廖邦固，徐建剛，宣國富，等.1947—2000年上海中心城區居住空間結構演變［J］ . 地理學報，2008，63（2）：195 - 206.

［8］ 牛俊蜻，呂園，劉科偉.城市規劃視角下西安市主城區住宅空間結構演變研究［J］ . 人文地理，2011，26（4）：48 - 53.

［9］ Fotheringham A.S., Brunsdon C, Charlton M. Geographically Weighted Regression［M］ . Chichester, UK: John Wiley and Sons, 2002.

［10］ Yu D. Spatially Varying Development Mechanisms in the Greater Beijing Area: A Geographically Weighted Regression Investigation［J］ . Annals of Regional Science, 2006, 40（1）: 173 - 190.

［11］ 覃文忠，王建梅，劉妙龍.混合地理加權回歸模型算法研究［J］ . 武漢大學學報：信息科學版，2007，32（2）：115 - 119.

［12］ McCord M, Davis P.T., Haran M, et al. Spatial variation as a determinant of house price:Incorporating a geographically weighted regression approach within the Belfast housing market［J］ . Joural of Financial Management of Property and Construction, 2012, 17（1）: 49 - 72.

［13］ Farber S, Pá ez A. A systematic investigation of cross-validation in GWR model estimation: empirical analysis and Monte Carlo simulations［J］ . Journal of Geographical System, 2007, 9（4）: 371 - 396.

［14］ Wang N, Mei C.L., Yan X.D. Local linear estimation of spatially varying coefficient models:an improvement on the geographically weighted regression technique［J］ . Environment and Planning A, 2008, 40（4）: 986 - 1005.

［15］ Hurvich C.M., Simonoff J.S., Tsai C.L. Smoothing parameter selection in nonparametric regressi On using an improved Akaike information criterion［J］ . Journal of the Royal Statistical Society B, 1998, 60（2）: 271 - 293.

［16］ 梅長林，王寧.近代回歸分析方法［M］ . 北京：科學技術出版社，2012.

［17］ Robinson C, Schumacker R.E. Interaction effects: Centering,variance inflation factor and interpretation issues［J］ . Multiple Linear Regression Viewpoints, 2009, 35（1）: 6 - 11.

［18］ Mei C.L., He S.Y., Fang K.T. A note on the mixed geographically weighted regression［J］ . Journal of Regional Science, 2004, 44（1）: 143 - 157.

（本文責編：郎海鷗）

Local Linear Geographically Weighted Regression Analysis on the Urban Housing Price: A Case Study of Huangshi City, Hubei Province

WANG Xin-gang，KONG Yun-feng
（College of Environment and Planning, Henan University, Kaifeng 475001, China）

This paper aims to analyze the spatial variations of urban housing price and its impact factors using local linear geographically weighted regression （LLGWR） model. For purpose of real estate market management and land use policy making scientifically, Huangshi City, Hubei Province, a typical land-scarce, resource-based and multi-group city, is selected as the study area. Additionally, 193,00 housing units and 398 buildings are collected as modeling samples. Based on the general and spatial statistics, the floor numbers, the plot ratio, the greening ratio, the level of property management, the distance to nearest urban center, and the year of sale are selected as explanatory variables, constructing the model and carries on the analysis and interpretation. The modeling results indicate that, compared with ordinary linearregression （OLS）, GWR and LLGWR are more suitable for interpreting urban housing price, and LLGWR is better than GWR. The housing price is substantially affected by the year of sale, plot ratio and the urban geographic location; and it is also related to the building height and greening ratio. However, they have very different contributions in different urban functional zones. There are three findings from this research: 1） LLGWR model, using unbiased estimation of coefficient function and error variance, can improve estimation and prediction accuracy of the urban housing price; 2） Macro market trend is the key factors affecting the housing price, but in different geographical location, housing price growth trend is obvious difference; 3） The spatial distribution of real estate development is closely related to land use planning and land supply policy, however, the relationship between land price and housing price is not obvious in the study area.

real estate prices; housing price; local linear geographically weighted regression （LL-GWR）; Huangshi City

P208

A

1001-8158（2015）03-0082-08

10.13708/j.cnki.cn11-2640.2015.03.011

2014-04-29

2015-01-12

國家十二五科技支持計劃（2012BAJ051306）。

王新剛（1972-），男，河南鄭州人，博士研究生。主要研究方向為城市問題和城市住房。E-mail: wuhanwxg@163.com