運動目標的超前預測跟蹤

左 韜

（武漢科技大學信息科學與工程學院，湖北 武漢430081）

0 前言

運動目標跟蹤廣泛應用在雷達、視頻跟蹤、無線激光通信、天文觀測、航空攝影等領域，現有的運動目標跟蹤方法一般都是在取得目標運動狀態觀測值的情況下，應用濾波方法得到狀態的最優估計值，這種方法可以大幅度減小噪聲對跟蹤的影響，但卻無法克服跟蹤的滯后。在觀測噪聲影響不大的情況下，本文對運動目標的狀態采取卡爾曼濾波先驗預測，可提前一步預測目標的運動狀態，跟蹤執行機構可超前預測跟蹤，從而克服跟蹤的滯后。

1 目標運動模型

采用“當前”統計模型建立目標運動模型[1]，得到目標運動的狀態描述。該模型用修正的瑞利分布來描述加速度的“當前”概率密度，本質上是非零均值時間相關模型。以x（t）表示目標的位置，表示目標的速度，表示目標的加速度，則狀態向量為：

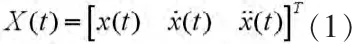
目標運動的“當前”統計模型非零均值狀態方程表示為：

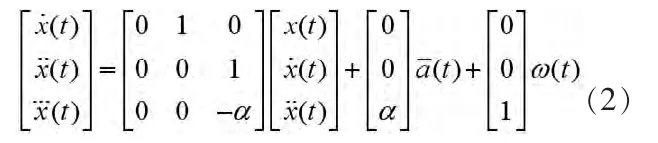
采樣周期為T時的離散狀態方程為

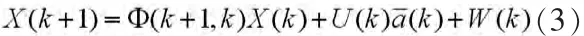
觀測方程為

W（k）、V（k）為均值為0的離散高斯白噪聲序列，當只有位置數據可直接觀測時，H（k）=［1 0 0］。

采用“當前”統計模型描述目標的運動狀態，符合機動運動的實際特性，能較好的反映目標機動范圍和強度的變化，且響應速度快、跟蹤精度高。

2 卡爾曼濾波預測

對運動目標建立當前“統計”模型狀態方程和觀測方程之后，由卡爾曼濾波[3]可得到目標運動狀態的預測值和最優估計值，卡爾曼濾波由如下核心方程組成：

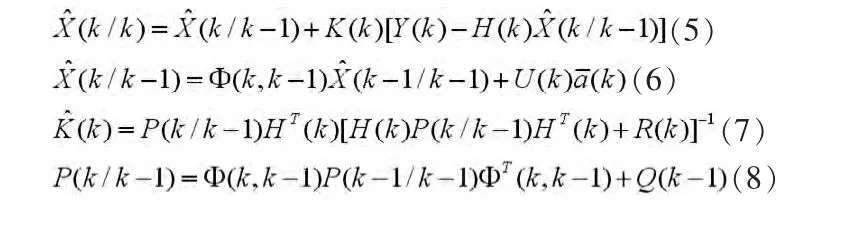
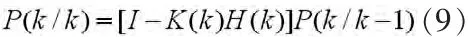
本文采用公式(6)實現對目標運動狀態的超前一步預測，也就是由已知的運動狀態預測下一時刻的運動狀態，從而克服跟蹤的滯后，超前預測值是一種先驗預估，預測精度低于后驗最優估值，雖然損失了精度，但可以提前一步預測跟蹤，在跟蹤滯后嚴重的情況下，可以取得較好的跟蹤效果。

3 仿真分析

通過跟蹤一個變速直線運動的目標來驗證超前預測跟蹤的性能。采樣周期T為1秒，仿真時間130秒，目標初始位置在0.05km處，前100 s做0.05km/s的勻速運動，101-130 s做0.0005 km/s2的勻加速運動，觀測噪聲方差為0.02，均值為0。

對運動目標做位置跟蹤，仿真結果如圖1、2所示。圖1為目標的真實位置與超前預測位置分布，可見預測位置非常逼近真實位置曲線，圖2為目標位置的超前預測誤差曲線，其均方根誤差為0.0518 km。

圖1 目標位置超前預測

圖2 超前預測誤差

4 結論

本文建立機動目標的當前統計運動模型，對運動目標采用卡爾曼濾波預測跟蹤，可超前一步預測目標的運動狀態，通過仿真分析，驗證了對變速運動目標的位置超前預測有較好的跟蹤效果，可有效克服跟蹤的滯后。

［1］周宏仁，敬忠良，王德培．機動目標跟蹤[M]．北京：國防工業出版社，1991.

［2］Jianfeng Wu,Gang Li,Fuzhou Ma.Research on target tracking algorithm using improved current statistical model[C]//2011 International Conference on Electrical and Control Engineering.2515-2517.

［3］Vinaykumar,M.,Jatoth,R.K..Performance evaluation of Alpha-Beta and Kalman filter for object tracking[C]//2014 International Conference on Advanced Communication Control and Computing Technologies.2014,1369-1373.