MPC算法在機載傳感器規劃中的應用

張 歡，吳 軍，何貴波，吳志峰

（1.空軍工程大學航空航天工程學院，陜西 西安 710038;2.中國人民解放軍93256部隊，遼寧 沈陽 110034）

0 引言

隨著任務規劃系統的不斷發展，人們對機載傳感器規劃的研究也陸續開展起來，傳感器規劃用于作戰飛機在完成任務執行過程中對自身的機載傳感器使用計劃的制定，其中包括對傳感器的選用、使用時機、使用策略等［1］，并對使用后的效果進行分析，評估達成任務目的的可行性，以此更好地發揮裝備的作戰效能和完成作戰任務。傳感器規劃與航線規劃密切相關，通常是在航線規劃完成以后開始實施，以航線中的某個位置作為使用時機開展傳感器的使用計劃制定工作，當使用時機不能滿足既定的目標要求時，需要及時調整使用時機或對航線進行修改。

本文將主要探究在傳感器規劃過程中如何根據目標的狀態來設置傳感器的使用時機、使用策略，如何實時跟蹤捕捉到目標，以及如何將捕捉到的信息及時反饋回來，以便能夠實時地對飛行航線進行局部調整。為此，本文提出了一種改進的模型預測控制（model prediction control，MPC）算法，該算法將傳統MPC的基本思想［2］與卡爾曼濾波中的目標狀態估計理論相結合，仿真結果表明:該算法在解決傳感器探測跟蹤移動目標方面具有良好的效果，能夠比較準確、快速地搜索到移動目標。

1 MPC基本思想

MPC是20世紀70年代在工業控制領域出現的一種新型控制算法，該算法的基本思想是在每個推進步長中先預測未來的輸出狀態，然后確定控制動作。在下一個推進步長中重復進行優化過程，并保持原有的優化性能指標不變，改變其作用區域，以此體現MPC算法在線滾動優化特點。常規MPC主要包含3個基本的要素:預測模型、滾動優化和反饋校正［2］。

1）預測模型

預測模型用來表述對象的輸入輸出動態行為，就是根據對象的歷史信息和未來輸入來確定對象的未來輸出。

2）滾動優化

滾動優化是一種基于優化的控制，通常情況下，是根據某一性能指標的最優來確定未來的控制作用，其數學描述一般為:設預測時域為m個步長，控制時域為n個步長，n≤m，在尋優的過程中，對于任意時刻j，通過上述推進步長可計算出對應的控制序列，直至尋優結束。因此，可定義目標函數為

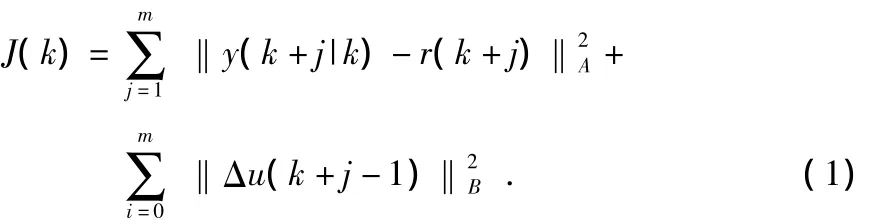
滾動優化實質上是對目標函數在線不斷滾動尋優的過程。

3）反饋校正

反饋校正環節用于補償模型預測誤差或其它干擾因素所產生的擾動。

2 算法基本流程

在基于MPC的傳感器規劃算法中，首先需要做的是構建一個初始搜索圖C（D，S），對于任意一點r∈R，在該圖中都存在一條邊s∈S，滿足r∈FOR（s），其中，FOR為傳感器能夠覆蓋到的所有目標探測區域，接下來將利用已有的信息對搜索圖進行初始化。假設載機的起始位置為點d0，隨機選取3個點d1，d2和d3作為初始任務點，由這4個點構成一條初始航線P=（d0，d1，d2，d3）與相應的傳感器計劃L（P，0）。在載機沿著初始的航線P從起始點d0飛到任務點d1的過程中，傳感器根據初始的傳感器計劃L（P，0）對目標區域進行探測，并根據探測的結果對目標區域的目標估計信息進行更新。同時計算出未來的飛行航線P=（d1，d2，d3，…，di+3）和對應的傳感器計劃L（P，i），使得期望的航線收益（P）達到最大。當載機到達任務點d1之后，就以d1作為新的起始點，滾動優化重復以上步驟，直到最終發現目標。最后，分析此次傳感器規劃過程中傳感器的使用效果，并對是否達成作戰目的的可行性做出評估分析。

基于MPC的傳感器規劃算法的具體流程圖如圖1所示。

接下來主要針對算法流程中的初始搜索圖如何構建、傳感器計劃L的定義、航線收益R（p）的計算、基于卡爾曼濾波理論的目標狀態估計模型的建立以及如何分析傳感器的使用效果等幾個方面進行剖析。

2.1 初始搜索圖的構建

在搜索圖問題中，以圖的頂點表示航線點，2個頂點之間的連線表示一條航段，通常將圖整體記為C，將圖C中的全體頂點構成的集合記為D，圖C中的全部邊構成的集合記為S，并記C=（D，S），圖搜索問題的本質實際上就是在滿足給定約束指標的前提下，在圖中尋找出一條最優的航線［4］。如圖2所示為一個基本的圖模型，其中d1～d9為航線點，s1～s9表示航段，航段未完全標出。

有了基本圖模型之后，可根據基本圖模型來構建搜索圖。在一片搜索區域R上構造一個四邊形均勻網格圖C=（D，S），網格圖C必須滿足如下條件:對于搜索區域R內的任意一點r，都有與之相對應的一條邊s∈S，能夠保證r落在邊s上的某些點的傳感器可探測區域（FOR）內，由此可以確定圖內的任意一點傳感器都能夠探測到。

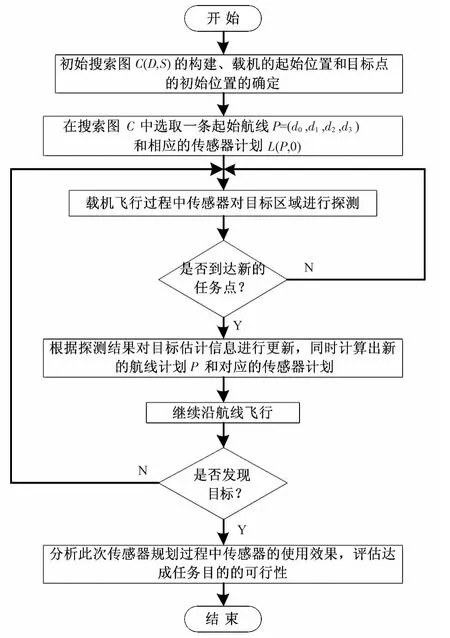
圖1 基于MPC的傳感器規劃算法流程圖Fig 1 Flow chart of sensor planning algorithm based on MPC

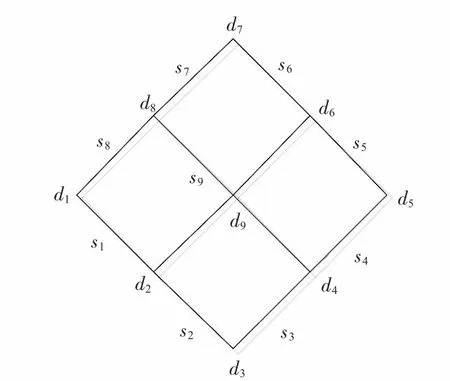
圖2 基本圖模型Fig 2 Basic graph model

某型作戰飛機在執行任務之前，首先需根據已有的先驗情報信息對搜索圖進行初始化，利用目標狀態估計理論所獲取的目標信息對網格圖C中的目標信息進行初始化。如圖3所示為構建的初始搜索圖，圖上的點d0為載機的初始位置，點d1，d2和d3為預先選取的3個任務點，圖上的小黑點為搜索圖初始化后目標估計的位置分布情況。

2.2 傳感器計劃的定義

1）傳感器視場（FOV）和觀測場（FOR定義）

傳感器在地面上的瞬時探測區域稱為傳感器的視場，即為FOV，觀測場FOR則是隨著載機的移動和對傳感器進行的一些操作，FOV在地面上不斷移動，進而形成的載機對地面的全部探測范圍稱之為觀測場［5］。如圖4所示為某型機載雷達的探測視場示意圖。

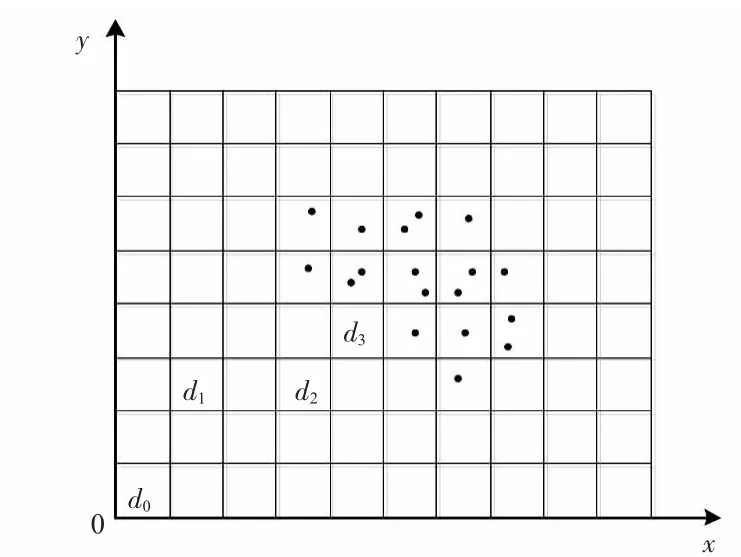
圖3 構建的初始搜索圖Fig 3 Builded initial search graph

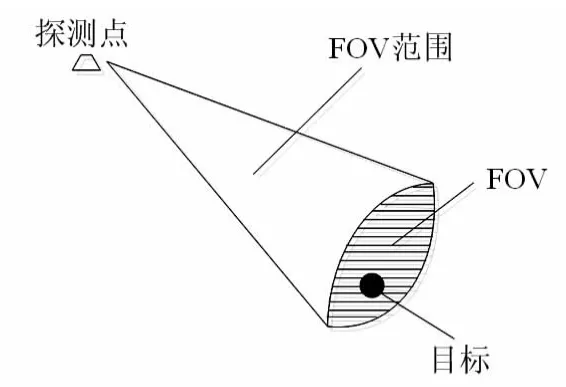
圖4 傳感器視場FOV示意圖Fig 4 FOV diagram of sensor field

由圖4可以看出:FOV范圍的大小由傳感器的探測點和視場大小決定，由于FOV的大小一般由傳感器的系統參數決定，并且在一定范圍以內其值通常不變，為常數。因此，在研究傳感器規劃問題中，通常用傳感器的觀測點來描述傳感器規劃問題。

2）傳感器任務的定義

假設i時刻傳感器的觀測點為q（i），則指向q（i）的傳感器視場定義為FOV（q（i）），一個作用在FOV（q（i））范圍內的時延定義為一個傳感器任務，記為q（i）［6］。

傳感器任務的序列稱為傳感器計劃，一般來講，一個傳感器計劃是由多個傳感器任務序列組合而成的，屬于離散范疇內的對象，因此，可記為

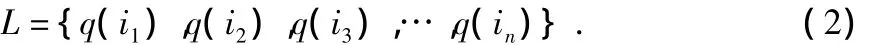
2.3 航線收益計算

定義i時刻傳感器的瞬時搜索增益為r（i），其含義實質上為i時刻發現目標的概率，如果一個目標處于傳感器的FOV內且被發現了，則收益為1，傳感器初始搜索收益為r（0）=0。傳感器的下一步搜索收益一般由傳感器任務q（i）、當前的目標狀態估計值設為x（i）和當前搜索收益決定，其計算式

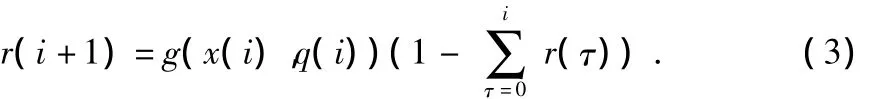
式中 函數g的值為i+1時刻目標被發現的概率。

航線P的收益可定義

式中TP為航線P上所有的可能執行的傳感器任務總數，r（τ）為 τ 時刻傳感器的搜索收益［7］。

2.4 目標狀態估計模型建立

本文采用了卡爾曼濾波器來估計目標的狀態分布，卡爾曼濾波是一種經典的、最優估計的遞推濾波算法，具有精度高、實時性好的特點［8］。設目標的卡爾曼濾波狀態方程

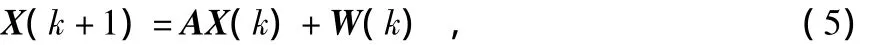
式中 X（k）為k時刻目標的狀態向量，X（k）∈Rn，A為k時刻狀態轉移矩陣，W（k）則是均值為0的高斯白噪聲。

假設目標的位置可表示為

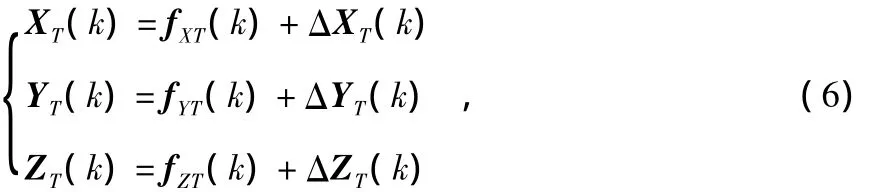
式中 f函數表示k時刻目標的真實位置，ΔX（k）則表示誤差量，則可將上式用矩陣形式表示為

將公式（7）作為卡爾曼濾波的量測方程，其中C表示狀態信號與輸出信號之間的增益矩陣。

可進一步求出誤差協方差矩陣為

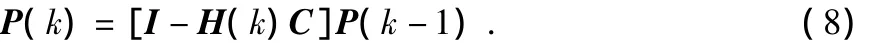
增益矩陣

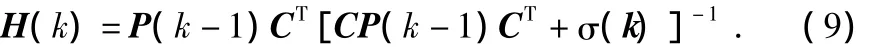
X（k）的狀態估計值

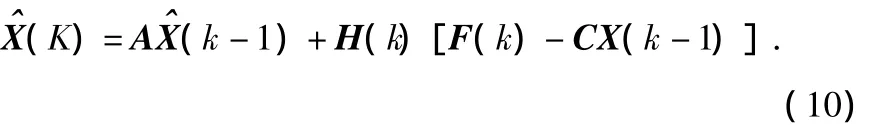
測量噪聲方差陣為

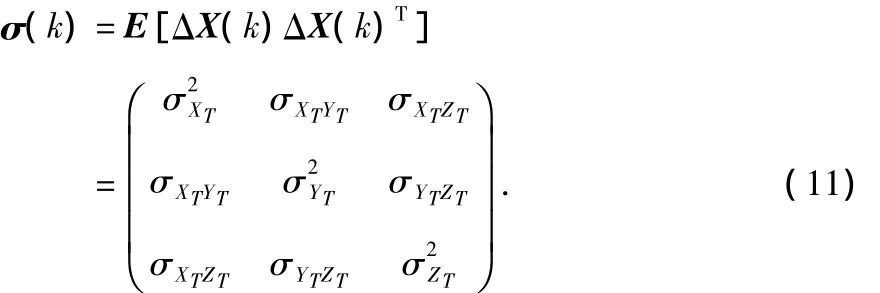
式（5）～式（11）組成了以卡爾曼濾波理論為原理的目標狀態估計模型。

2.5 傳感器使用效果分析

在每進行完一次傳感器規劃之后，應當對此次規劃過程中的傳感器使用效果進行分析，如圖5所示為某機載雷達使用效果分析圖。

從上圖中可以看出:為了檢驗機載雷達的使用效果，在雷達規劃組件中將用戶設置的雷達操控參數、使用時機、載機的即時位置與姿態信息、目標/目標區信息、氣象信息等發送到雷達模型，接收其作用范圍、可探測度等使用效果的計算結果，并以圖形化方式進行直觀顯示［10］。

分析完MPC算法基本流程中的關鍵要點之后，接下來通過仿真驗證該算法在傳感器規劃過程中的使用效果、算法的合理性。

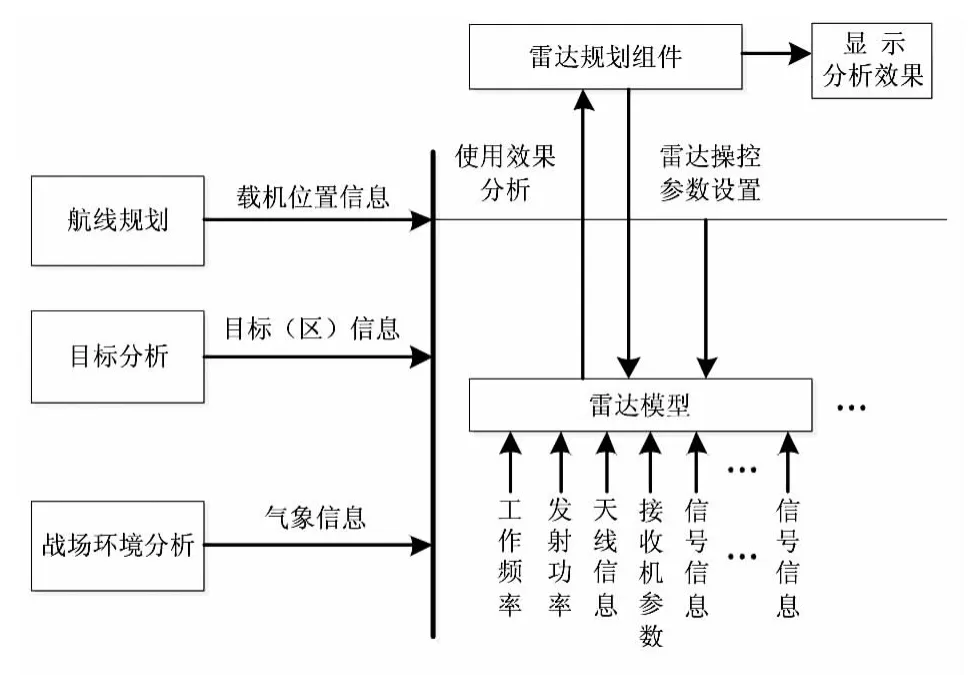
圖5 機載雷達使用效果分析圖Fig 5 Using effect analysis diagram of airborne radar

3 算法仿真驗證

仿真實驗采用VS2010編程軟件，利用之前介紹的圖搜索原理，選取了一片50 km×50 km的網格式任務區域，該區域作為傳感器對移動目標的搜索區域。假設目標以近似勻速直線方式運動，卡爾曼濾波系統的初始參數設置如下

如圖6所示為仿真實驗效果圖。其中，點1為執行任務的載機起飛點，點2、點3、點4、點5、點6為航線點，也即為任務點，在這5個航線點上將載機攜帶的傳感器設備（只考慮機載雷達）也形象的標會了出來;圖中的小黑點是利用已有目標先驗情報信息，再運用上文中建立的卡爾曼目標狀態估計理論，得到的目標狀態初始分布;點7（圖中三角形）作為機載雷達最終探測到的目標點，在圖中只顯示了4個點7位置，這4個位置從上到下依次作為在雷達進行探測的過程中目標依次移動的4個位置。

從仿真結果圖中可以看出:當目標點在4個點7位置從上到下移動時，機載雷達能夠準確地探測到目標移動的位置，達到了對目標實時跟蹤的效果。因此，可以得出結論:基于MPC的傳感器規劃算法在解決移動目標搜索這一關鍵的傳感器規劃問題時，能夠快速、準確地搜索到移動的目標，基本達到了對目標的實時跟蹤效果。

4 結論

本文針對機載傳感器規劃過程中的移動目標搜索這一難題，將MPC的基本思想與經典卡爾曼濾波中目標狀態估計理論相結合，提出了一種基于改進MPC算法的傳感器規劃方法，在深入剖析了該算法的基本思想和算法流程中的關鍵要素之后，再通過具體的編程，仿真驗證了該算法在解決移動目標搜索這一傳感器規劃問題中的有效性、合理性。

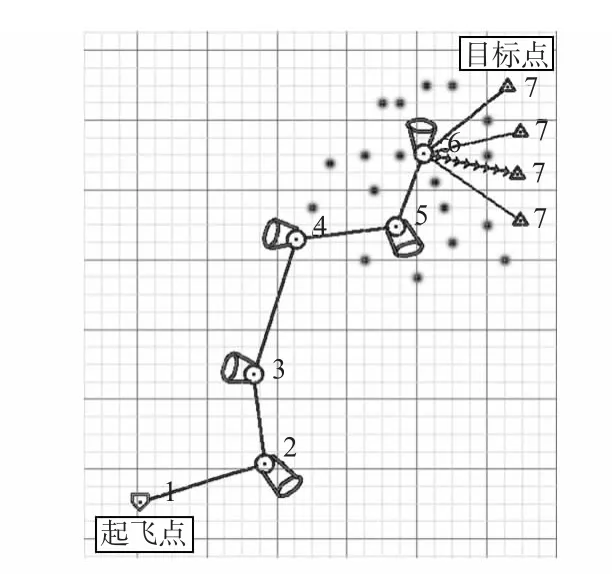
圖6 基于MPC算法的傳感器規劃仿真實驗結果圖Fig 6 Simulation result diagram of sensor planning based on MPC algorithm

［1］邢立寧，陳英武.任務規劃系統研究綜述［J］.火力與指揮控制，2006，31（4）:1-4.

［2］王文博.模型預測控制的抗擾性能分析［D］.杭州:浙江大學，2012.

［3］霍德聰.戰術飛機打擊任務中的傳感器使用策略與規劃方法研究［D］.長沙:國防科技大學，2007.

［4］Collins G E，Riehl J R，Philip S V.A UAV route and sensor control optimization algorithm for target search［R］.California:University of California，2007.

［5］Skoglar P，Nygards J，Bjorstrom R.Path and sensor planning framework applicable to UAV surveillance with EO/IR sensors［R］.Kista，Sweden:Totalforsvarets f?rskning sinstitut（FOI），2007.

［6］黃丁才.無人偵察機航線與傳感器規劃方法研究［D］.長沙:國防科技大學，2009.

［7］周 燕，范 鵬.戰術航空偵察航路規劃評價模型［J］.電光與控制，2007，14（1）:52-54.

［8］宗長富，胡 丹，楊 肖，等.基于擴展Kalman濾波的汽車行駛狀態估計［J］.吉林大學學報，2009，39（1）:7-11.

［9］任 佳，高曉光，趙歡歡.基于目標狀態估計的UAV路徑重規劃決策模型［J］.控制與決策，2009，24（7）:1033-1037.

［10］趙星辰.時間敏感目標的信息處理決策技術研究［D］.西安:空軍工程大學，2012.