雙基地MIMO雷達目標定位及幅相誤差自校正算法

李洪兵，姜 軍，田海林，季軍亮，郭藝奪

（空軍工程大學 防空反導學院，陜西 西安 710051）

0 引言

雙基地MIMO雷達的回波信號中包含了目標相對發射陣列的發射角及接收陣列的到達角信息，因此可通過估計目標的DOD，DOA實現對目標的交叉定位［1－8］。這些算法均以發射和接收陣列流型精確已知為前提，其性能優良。在實際工程應用中，由于存在各種誤差（陣元幅相誤差、陣元間互耦等），雙基地MIMO雷達的發射和接收陣列流形常出現一定程度的偏差或擾動，上述的各種定位算法因對模型誤差的魯棒性很差，微小的模型擾動會帶來目標定位性能的急劇惡化。因此，研究對誤差魯棒的目標定位算法及簡便有效的陣列校正方法在雙基地MIMO雷達實際應用中有重要意義。

雙基地MIMO雷達因發射端采用多個發射陣元發射相互正交的信號，其陣元通道的幅相誤差可通過接收陣列和發射陣元引入，從而使發射和接收陣列的幅相誤差耦合，這增加了系統幅相誤差的復雜度，對雙基地MIMO雷達的多目標定位和通道幅相誤差的校正提出了更高的要求。為解決此問題，文獻［9］提出了對信號預處理后等效陣列的聯合幅相誤差進行整體估計以實現誤差校正的方法，并針對單輔助目標的情況給出了子空間擬合法和最大似然法兩種誤差估計方法。但該算法對輔助目標方位信息的精確性有較高的要求，當輔助目標的方位信息有偏差時，該算法會產生較大的偏差。文獻［10］利用三次迭代最小二乘算法估計存在幅相誤差條件下的收發陣列流形，根據信號子空間和噪聲子空間的正交性，用 MUSIC-like算法獲得目標的DOD，DOA，且角度自動配對，然后針對MIMO雷達孔徑擴展的特點，通過第一個發射陣元和第一個接收陣元的數據估計收發陣列的幅相誤差。但該算法需要進行迭代運算和一維譜峰搜索，計算量較大，此外其假設將收發陣列第一個陣元的幅相誤差均歸一化為1，這與實際情況存在偏差。

收發陣列的幅相誤差的存在破壞了雙基地MIMO雷達的旋轉不變性，導致小運算量的ESPRIT算法無法直接用于估計目標的DOD，DOA。對此，本文對一種基于ISM的ESPRIT類算法進行了研究［11］。

1 基于ISM的雙基地MIMO雷達幅相誤差數據模型

考慮一發射陣列和接收陣列均為均勻線陣的雙基地MIMO雷達系統，其中發射陣元數為Mt，各發射陣元同時發射同頻相互正交的相位編碼信號；接收陣元數為Mr，且發射和接收陣元間距均為λ／2。設發射陣和接收陣之間的基線距離為D，滿足D?λ，并假設在雷達系統的遠場同一距離單元內存在目標P個，其相對發射及接收陣列的方位角為（φp，θp），p＝1，2，…，P。設Γt，Γr分別為發射和接收陣列的幅相誤差矩陣，且

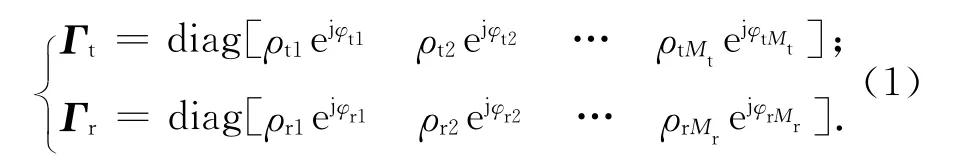
式中：ρtm，φtm分別為第m個發射陣元對應的幅值和相位誤差；ρrn，φrn分別為第n個接收陣元對應的幅值和相位誤差。此處：m＝1，2，…，Mt；n＝1，2，…，Mr。

為避免發射和接收陣列的幅相誤差的影響，本文用ISM分別在發射和接收端設置若干精確校正的陣元，并分別以引入的第一個發射和接收的輔助陣元為參考。設引入的輔助發射和接收陣元數分別為Nt，Nr（Nt，Nr≥2），輔助陣元同原有陣元的間距及輔助陣元之間的間距均為λ／2，如圖1所示。則此時的數據模型可表示為

式中：l＝1，2，…，L；（tl） 為經匹配濾波器后的整個雙基地MIMO雷達系統的虛擬噪聲，是均值為0、方差為σ2的高斯白噪聲；

符號“＊ ”、“? ”分別表示 Khatri-Rao，Kronecker的積。

圖1 基于ISM的雙基地MIMO雷達系統Fig.1 Bistatic MIMO radar system based on ISM

因此，其數據協方差矩陣可表示為

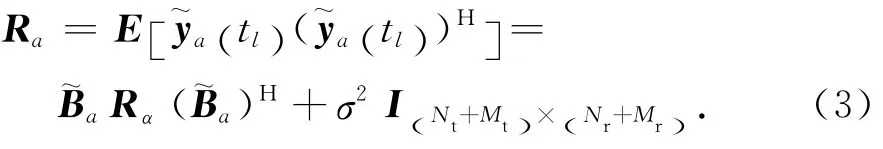
對Ra進行特征值分解可得相應的信號子空間Uas和噪聲子空間Uan。根據陣列流形矩陣與信號子空間間關系可知Uas與滿足關系

式中：T為一個唯一的非奇異矩陣。

在有限次脈沖數情況下，只能得到協方差矩陣的估值，對其進行特征值分解可得

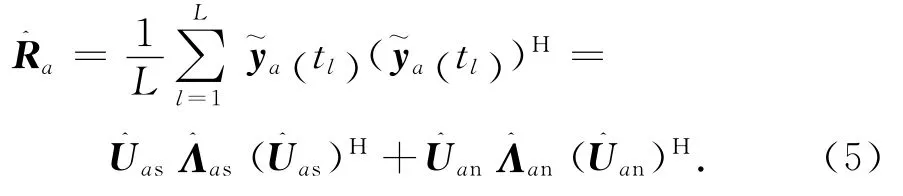
式中：為對進行特征值分解后得到的前P個大特征值形成的對角陣為剩余的小特征值形成的對角陣。

2 算法描述

定義矩陣

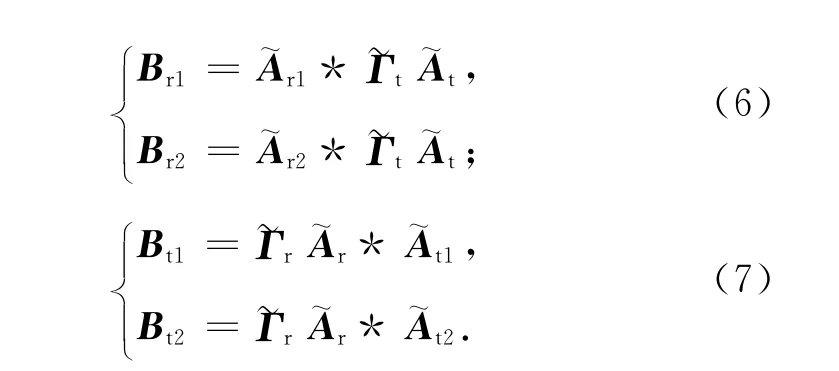
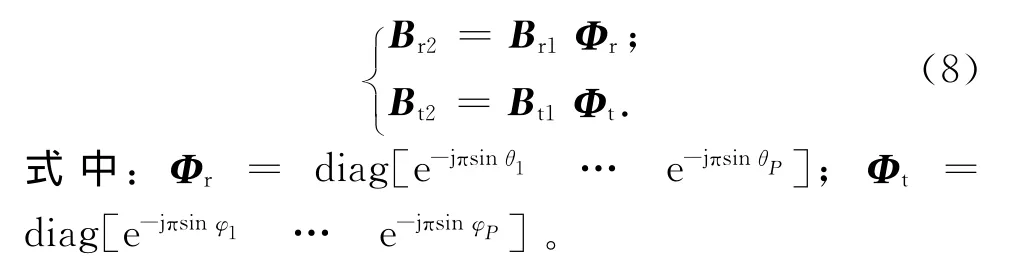
令Ur1，Ur2的構造方式與Br1，Br2相同，Ut1，Ut2的構造方式與Bt1，Bt2相同。根據式（6）可知，Ur1，Ur2和Ut1，Ut2分別滿足

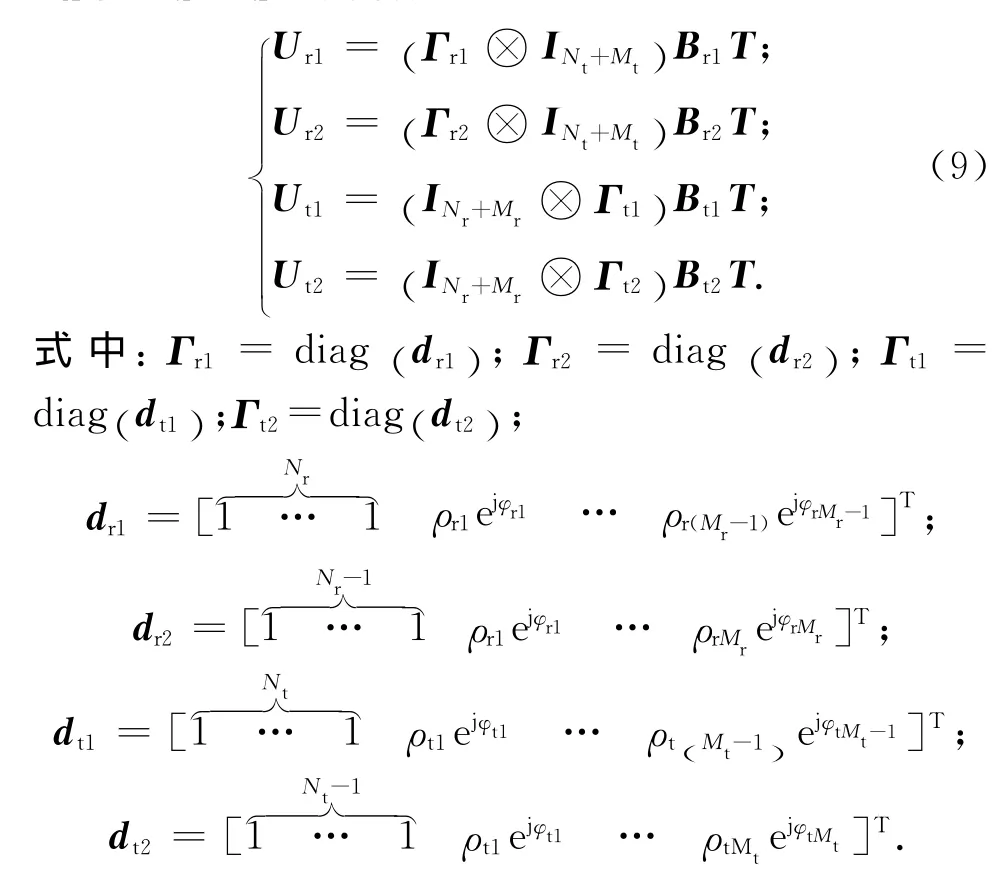
根據式（8）、（9）可得

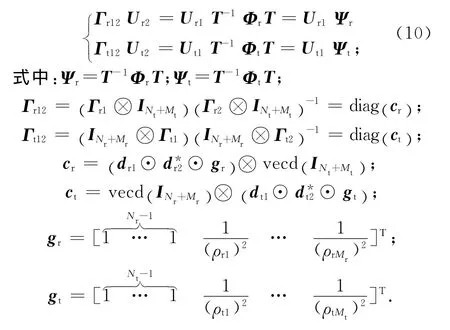
因Γr12，Ψr，Γt12，Ψt為未知，故可通過以下帶約束的優化問題求解

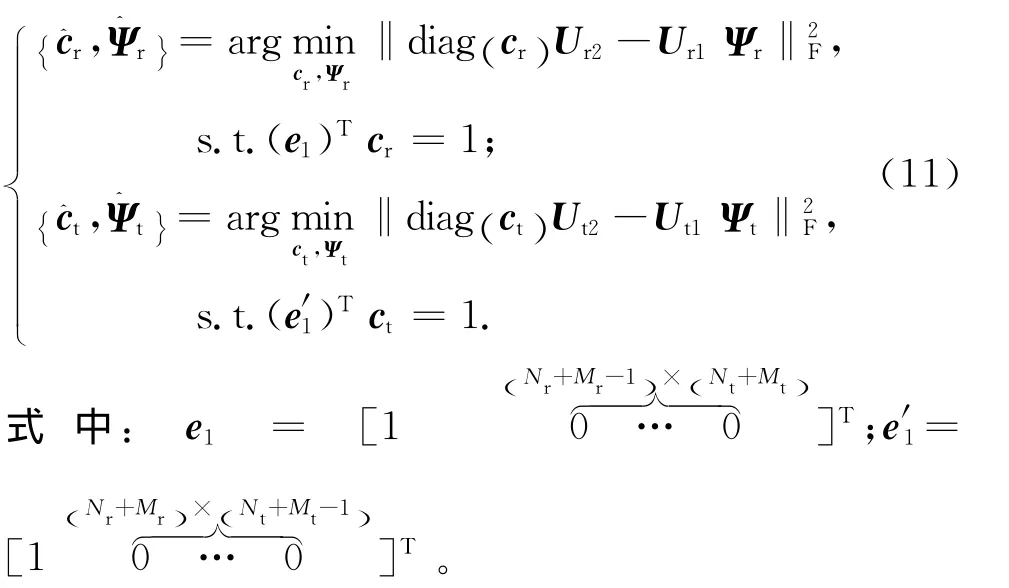
基于最小均方誤差準則，可得式（11）的解為

將式（12）代入式（11）可得

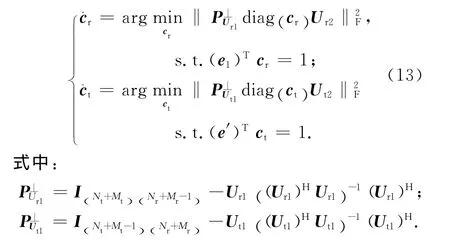
由文獻［12］，

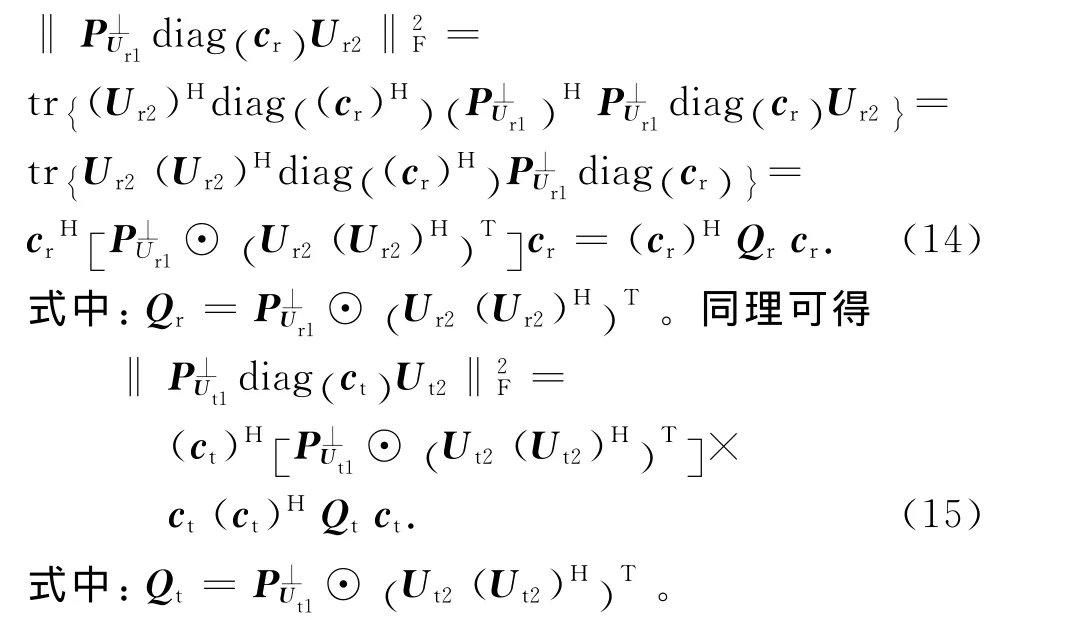
將式（14）、（15）代入式（13）可得

用Lagrange算子法對式（16）進行求解，可得

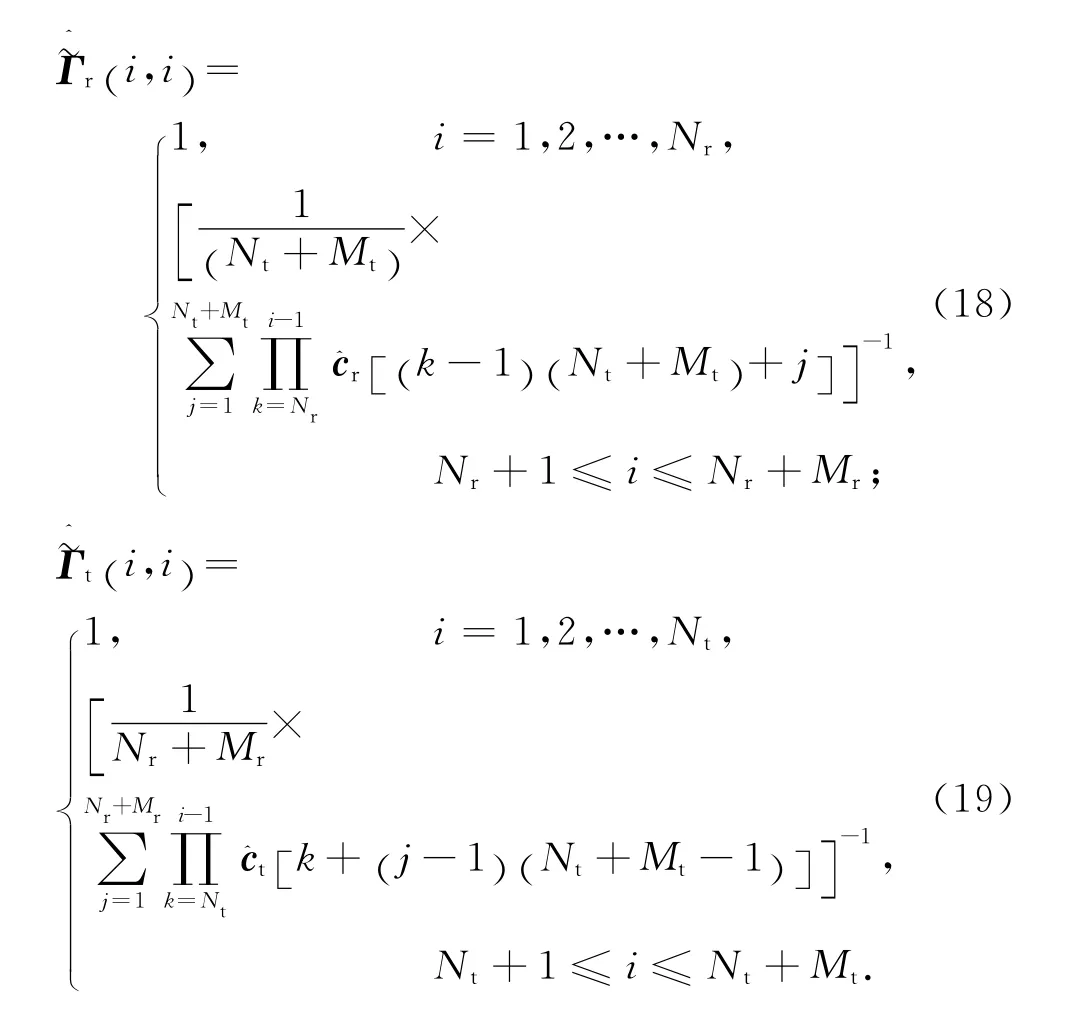
將式（17）代入式（12）可得對Ψr，Ψt的估值分別為

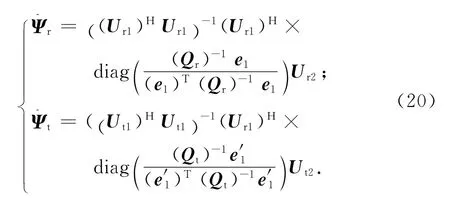
對進行特征值分解可得其特征值和特征向量分別為，則可得對目標DOA的估值為

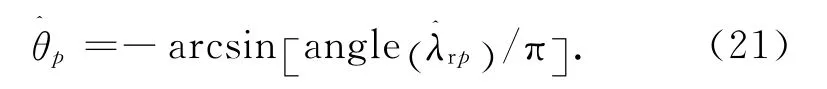
由Ψr，Ψt的表達式可知：對同一個目標，Ψr，Ψt具有相同的特征向量。因此，特征值由

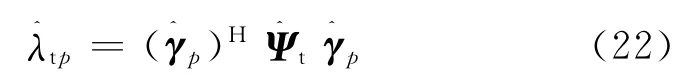
求得，從而可得對目標DOD的估值為

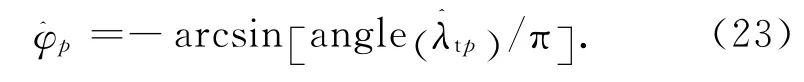
需指出的是：通過式（22）可避免對進行特征值分解，從而降低算法的計算量，同時還可實現對估計出的目標DOD，DOA的自動配對。

3 算法性能

根據上述算法的原理，可得定性結論如下。

a）算法在進行發射和接收幅相誤差校正過程中，無需任何精確校正的輔助目標，避免了輔助目標收發方位角誤差對幅相誤差參數估計的影響。

b）由于輔助發射和接收陣元引入的誤差自由度約束，本文算法克服了通常均勻線陣陣列校正中的模糊問題。因均勻線陣理想的導向矢量為范德蒙矢量，當發射和接收陣列的幅相誤差矢量vecdΓt，vecdΓr均有范德蒙特性時，二維方位估計與幅相誤差參數估計就會出現模糊，導致目標二維方位估計的偏差。但本文算法引入了精確校正的輔助發射和接收陣元，發射陣列擾動矢量vecd的前Nt個元素和接收陣列擾動矢量vecd的前Nr個元素均為1，不可能具有范德蒙性（除非陣元無擾動，vecd，vecd的元素均為1）。因此，本文算法消除了通常雙基地MIMO雷達擾動參數估計時由收發方位參數與幅相誤差參數耦合引起的模糊問題。

c）算法的運算量小，無需迭代和譜峰搜索過程，避免了高維、多模非線性搜索問題和局部收斂問題。

d）算法實現中未使用擾動導向矢量的一階泰勒近似對參數估計問題進行簡化，無需對陣列幅相誤差進行微擾動假設，更符合實際的誤差模型。

4 仿真與分析

為驗證所提算法的有效性，進行了仿真。取發射陣元數Mt＝5，接收陣元數Mr＝4，原發射陣列的幅值誤差系數和相位誤差系數分別為

原有接收陣列的幅值誤差系數和相位誤差系數分別為

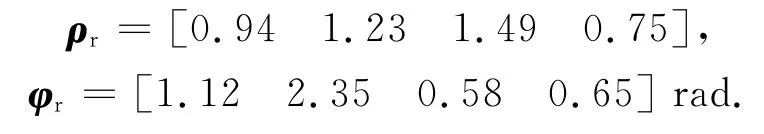
設空間中同一距離單元內存在目標3個，其收發方位角為（10°，20°），（－8°，30°），（0°，45°）。發射陣列各陣元發射相互正交的相位編碼信號，在每個脈沖重復周期內的快拍數K＝256。稱本文算法為ESPRIT－like算法，文獻［10］算法為 MUSIC-like算法。

仿真1：ESPRIT-like算法對目標定位結果

仿真中取引入的輔助發射和接收陣元數分別為Nt＝3，Nr＝2，信噪比10dB，脈沖數L＝256。ESPRIT-like算法對多目標定位結果如圖2所示。

由圖2可知：當發射和接收陣列均存在幅相誤差時，ESPRIT-like算法可較精確地估計出目標的DOD，DOA，且得出的參數可自動配對，可實現對多目標的定位。

仿真2：算法收發方位角估計統計性能

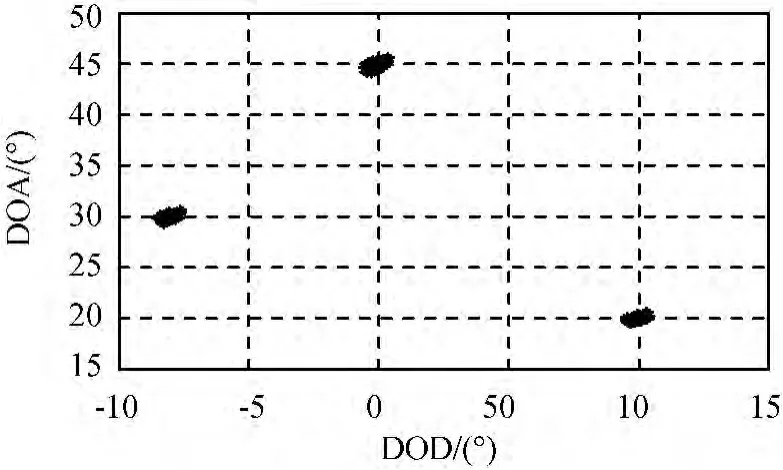
圖2 ESPRIT-like算法多目標定位結果Fig.2 Localization result of ESPRIT-like algorithm for multiple targets

仿真條件同仿真1，L＝256，不同信噪比（從0dB按步長2dB變化至40dB）時，ESPRIT-like，MUSIC-like算法對目標收發方位角估計的RMSE，如圖3所示。

由圖3可知：ESPRIT-like算法在估計目標收發方位角時無需任何幅相誤差信息即可達到較好的估計性能。與MUSIC-like算法相比，在較低信噪比或較小脈沖數條件下，ESPRIT-like算法的RMSE稍大于MUSIC-like算法，但隨著信噪比和脈沖數的增大，兩者的性能趨于一致。須注意的是ESPRIT-like算法可在無需任何迭代和譜峰搜索的情況下完成收發方位角估計，顯著降低了算法的運算量。

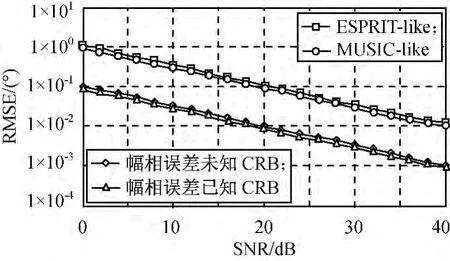
圖3 不同SNR時兩種算法的RMSEFig.3 RMSE for two algorithms under various SNR

仿真3：算法幅相誤差自校正性

為便于分析，定義發射和接收陣列幅值、相位誤差系數校正誤差為 ‖－ρt‖2／‖ρt‖2×100%，Δφt＝ ‖－φt‖2／ ‖φt‖2× 100%，Δρr＝‖－ρr‖2／ ‖ρr‖2× 100%，Δφr＝‖－φr‖2／‖φr‖2×100% 。此處：和ρt，φt分別為發射陣列幅值和相位誤差系數的估值及真值；和ρr，φr分別為接收陣列幅值和相位誤差系數的估值及真值。L＝256，信噪比從0dB按步長2dB變化到40dB時，ESPRIT-like，MUSIC-like算法的發射和接收陣列幅值和相位誤差系數校正誤差如圖4所示。圖4中同時給出了發射和接收陣列幅值、相位誤差系數估計的理論CRB曲線。

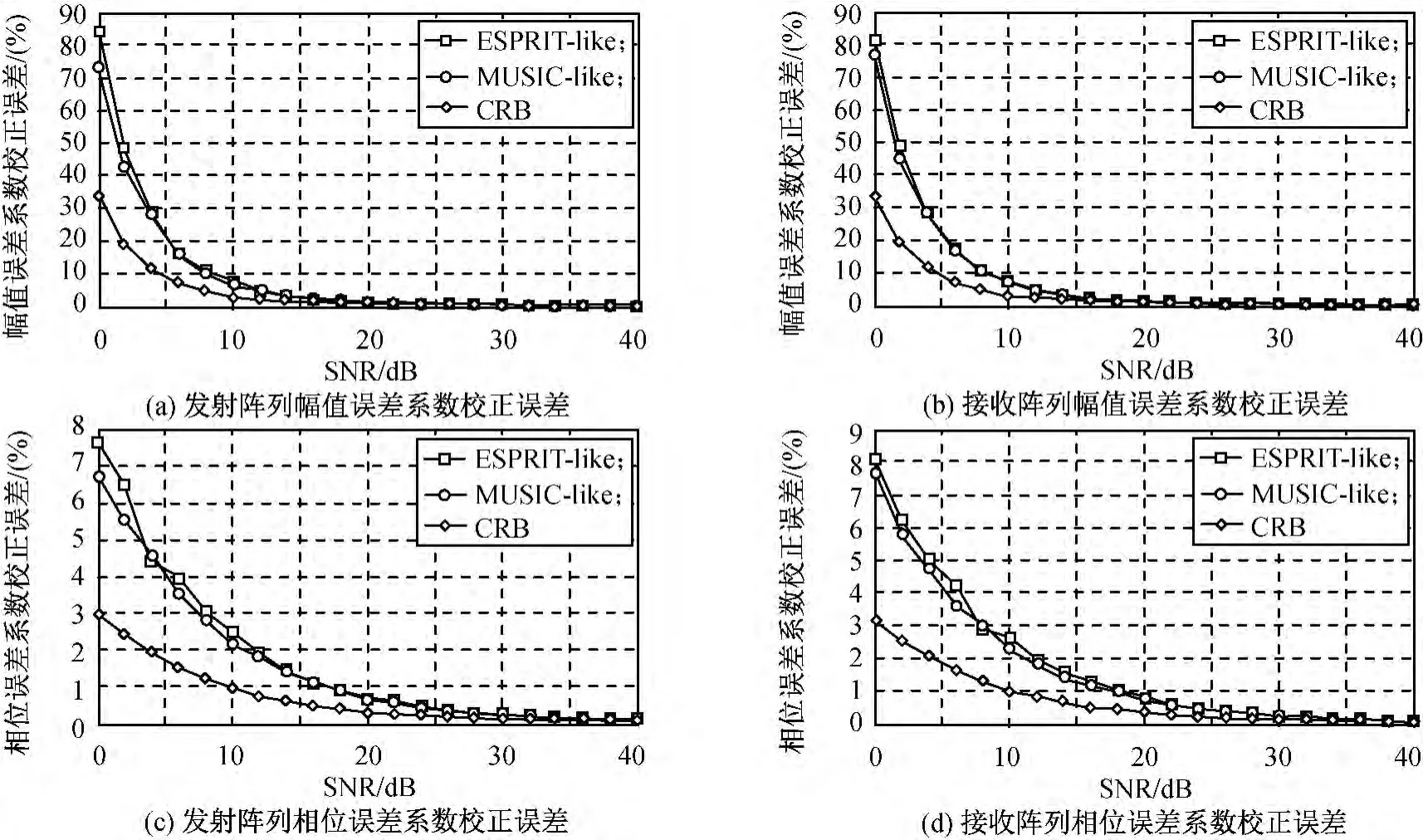
圖4 不同SNR的幅相誤差系數校正誤差Fig.4 Calibrated errors with gain and phase error coefficient under various SNR

由圖4可知：ESPRIT-like算法的幅相誤差系數校正誤差與 MUSIC-like算法基本相當。隨著SNR的增大，幅相校正誤差接近于0，這表明幅相誤差矩陣接近于真值。

5 結束語

本文針對雙基地MIMO雷達收發陣列存在幅相誤差的目標定位問題，提出了一種低運算量的目標定位及雙基地MIMO雷達收發陣列幅相誤差自校正的ESPRIT-like算法。該算法通過在發射端和接收端分別引入少量精確校正的輔助發射和接收陣元，可在多目標條件下對目標收發方位角和其對應的發射和接收陣元幅相誤差進行無模糊聯合估計。分析表明：在角度估計和幅相誤差自校正過程中無需任何收發陣列幅相誤差系數信息，且具有優良的目標定位及幅相誤差自校正性能，計算量小。

［1］ DANIEL J R，PARKER P.Ubiquitous MIMO multifunction digital array radar［C］／／Conference Record of the 37th Asilomar Conference on Signals，Systems and Computers.Pacific Grove：IEEE，2003：1057-1064.

［2］ FISHLER E，HAIMOVICH A，BLUM R.MIMO radar：an idea whose time has come［C］／／Proceedings of IEEE National Radar Conference.Philadelphia：IEEE，2004：71-78.

［3］ LI J，STOICA P.MIMO radar signal processing［M］.New Jersey：John Wiley ＆Sons Press，2009：235-251.

［4］ CHEN D F，CHEN B X，QIN G D.Angle estimation using ESPRIT in MIMO radar［J］.Electronics Letters，2008，44（12）：770-771.

［5］ YANG M L，CHEN B X，YANG X Y.Conjugate ESPRIT algorithm for bistatic MIMO radar［J］.Electronics Letters，2010，46（25）：1692-1694.

［6］ 陳金立，顧 紅，蘇衛民.一種雙基地 MIMO雷達快速多目標定位方法［J］.電子與信息學報，2009，31（7）：1664-1668.

［7］ JIN M，LIAO G S，LI J.Joint DOD and DOA estimation for bistatic MIMO radar［J］.Signal Processing，2009，89（2）：244-251.

［8］ GUO Y D，ZHANG Y S，TONG N N.Beamspace ESPRIT algorithm for bistatic MIMO radar［J］.Electronics Letters，2011，47（15）：876-878.

［9］ 楊明磊，張守宏，陳伯孝，等.多載頻MIMO雷達的幅相誤差校正［J］.系統工程與電子技術，2010，32（2）：279-283.

［10］ 劉曉莉，廖桂生.雙基地MIMO雷達多目標定位及幅相誤差估計［J］.電子學報，2011，39（3）：598-601.

［11］ WANG B H，WANG Y L，CHEN H，etal.Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors［J］.Science in China Ser F：Information Sciences，2004，47（6）：777-792.

［12］ 張賢達.矩陣分析與應用［M］.北京：清華大學出版社，2004.