陀螺轉(zhuǎn)子質(zhì)量偏心對末制導(dǎo)炮彈彈道特性的影響
佟德飛,宋衛(wèi)東,賈 波
(1.軍械工程學(xué)院 火炮工程系,石家莊050003;2.西安軍代局,西安710043)
某型末制導(dǎo)炮彈的慣導(dǎo)飛行控制是通過計算慣導(dǎo)陀螺外框架相對彈體的偏轉(zhuǎn)角度并形成指令,進而控制舵機偏轉(zhuǎn)完成的。陀螺外框擺角的計算通過彈體坐標(biāo)系、慣導(dǎo)陀螺坐標(biāo)系以及地面坐標(biāo)系之間相對角位置關(guān)系進行推導(dǎo)得出[1]。然而該計算方式以轉(zhuǎn)子軸方位相對于慣性空間不變?yōu)榍疤幔且环N理想情形,并未考慮陀螺轉(zhuǎn)子因動力學(xué)的作用產(chǎn)生定向性的變化。理論上,為了保證陀螺的定向性,陀螺轉(zhuǎn)子質(zhì)心應(yīng)該位于內(nèi)框軸和外框軸的交叉點位置,但由于工藝控制原因,轉(zhuǎn)子質(zhì)心與內(nèi)框框架幾何中心存在一定程度的偏離,因而產(chǎn)生偏心力矩導(dǎo)致轉(zhuǎn)子進動。本文在已有研究的基礎(chǔ)上,運用動量矩定理[2]研究轉(zhuǎn)子質(zhì)量偏心條件下的定向特性,結(jié)合末制導(dǎo)炮彈六自由度剛體彈道模型以及慣導(dǎo)控制模型[1],考慮慣導(dǎo)陀螺質(zhì)量偏心引起的控制誤差對彈道特性產(chǎn)生的影響。
1 陀螺運動狀態(tài)方程描述
為描述慣導(dǎo)陀螺轉(zhuǎn)子的運動,首先建立其空間坐標(biāo)系。設(shè)轉(zhuǎn)子的幾何中心與內(nèi)框架、外框架幾何中心O重合,以O(shè)為原點,將慣性坐標(biāo)系平移至原點建立陀螺基準(zhǔn)坐標(biāo)系Oξηζ,η軸鉛垂向上。令Oξηζ繞η軸轉(zhuǎn)過ψgd角,再繞ζ軸新位置轉(zhuǎn)過θgd角,建立轉(zhuǎn)子動量矩坐標(biāo)系OXYZ,其中X軸為轉(zhuǎn)子相對原點的動量矩矢量方向,動量矩為L,其中ψgd,θgd為動量矩坐標(biāo)系相對慣性坐標(biāo)系的旋轉(zhuǎn)角度。令OXYZ繞X軸轉(zhuǎn)過γgd角后的位置為轉(zhuǎn)子的主軸坐標(biāo)系Oxryrzr,xr軸為轉(zhuǎn)子的對稱軸,如圖1所示。參考文獻[3]中對陀螺內(nèi)外框架坐標(biāo)系的描述,本文將轉(zhuǎn)子主軸坐標(biāo)系繞yr軸轉(zhuǎn)過ψg角,建立慣導(dǎo)陀螺內(nèi)框坐標(biāo)系Ox1y1z1,再繞z1軸旋轉(zhuǎn)θg角(此角度即為慣導(dǎo)陀螺外框擺動角),建立外框架坐標(biāo)系Ox2y2z2,如圖2所示。轉(zhuǎn)子質(zhì)心相對幾何中心的偏心距矢量為er,er取在轉(zhuǎn)子主軸坐標(biāo)系。分別研究轉(zhuǎn)子在軸向、徑向存在質(zhì)量偏心時產(chǎn)生的動力學(xué)作用。

圖1 動量矩坐標(biāo)系角度坐標(biāo)
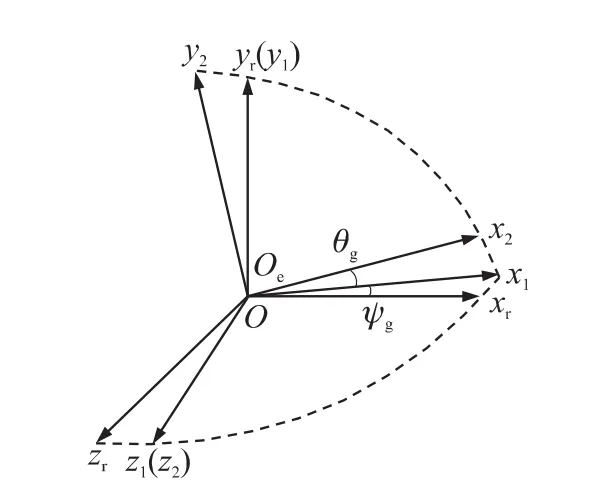
圖2 轉(zhuǎn)子相對動量矩坐標(biāo)系偏轉(zhuǎn)角度坐標(biāo)
1.1 轉(zhuǎn)子運動狀態(tài)方程
偏心距矢量在慣性坐標(biāo)系下表示為e=PT(γgd,θgd,ψgd)er,PT(γgd,θgd,ψgd)為慣性系向轉(zhuǎn)子主軸坐標(biāo)系投影矩陣,寫成分量形式:
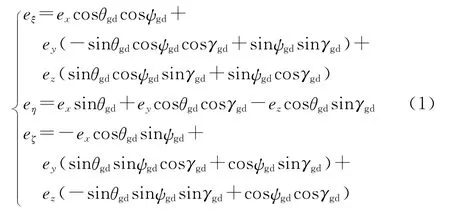
慣性系中,重力加速度表示為g=(0 -g0)T。由于存在質(zhì)量偏心,則偏心力矩為M=e×mg,其在慣性坐標(biāo)系中的分量為
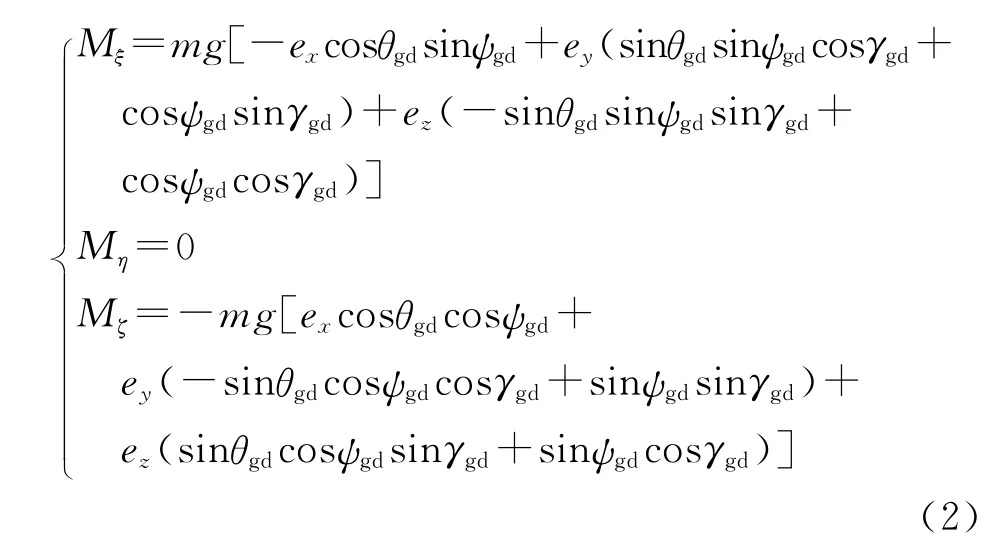
再將轉(zhuǎn)子動量矩矢量投影至慣性坐標(biāo)系,則
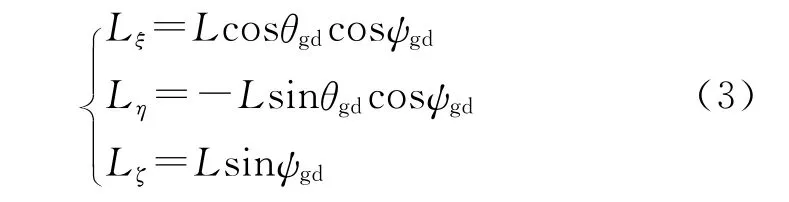
將式(1)~式(3)代入動量矩定理dL/dt=M。由于存在dLη/dt=0的情況,則轉(zhuǎn)子動量矩在慣性系的垂直方向守恒,因此-Lsinθgdcosψgd與動量矩在慣性系垂直分量的初值一致,存在初始的偏角,即

對式(3)兩端進行求導(dǎo),則可以得到和,分別表示為

忽略微小偏心對主軸慣性主矩的影響[4],設(shè)轉(zhuǎn)子極軸慣性主矩為C,轉(zhuǎn)動角速度為Ω,轉(zhuǎn)子轉(zhuǎn)動的動量矩大小為L0=CΩ。
1.2 內(nèi)、外框架運動狀態(tài)方程
將轉(zhuǎn)子偏心力矩分別向轉(zhuǎn)子內(nèi)框坐標(biāo)系Ox1y1z1、外框坐標(biāo)系Ox2y2z2進行投影,得到:

根據(jù)對轉(zhuǎn)子內(nèi)、外框廣義自由坐標(biāo)的定義,繞軸轉(zhuǎn)動運動方程是獨立的,而其余方向的運動是非獨立的,反映內(nèi)、外框軸之間的力矩關(guān)系,則僅僅給出影響框架轉(zhuǎn)動運動的狀態(tài)方程,即

為簡化起見,式中將轉(zhuǎn)子軸相對于慣性坐標(biāo)系的方向余弦記為dij,i,j=1,2,3。
1.3 外框架偏轉(zhuǎn)角度計算
外框架偏轉(zhuǎn)角度的計算方法仍通過幾何關(guān)系的轉(zhuǎn)換求解,求解關(guān)系式為

式中:γ,φ,ψ為末制導(dǎo)炮彈彈體姿態(tài)角;γg為慣導(dǎo)陀螺相對彈體的安裝角。隨著轉(zhuǎn)子偏心力矩的不斷作用,慣導(dǎo)陀螺轉(zhuǎn)子產(chǎn)生進動,定向性發(fā)生改變,轉(zhuǎn)子姿態(tài)角的計算可由初始定向角和進動偏移角度進行疊加。內(nèi)、外框偏轉(zhuǎn)角度的值由幾何關(guān)系求解得到,原計算方法中的轉(zhuǎn)子定向角度由進動后轉(zhuǎn)子姿態(tài)角度替換。
2 陀螺運動狀態(tài)數(shù)值仿真
陀螺轉(zhuǎn)子角度變化以及動量矩的變化均可通過積分進行求解。轉(zhuǎn)子受到外力矩的作用,產(chǎn)生與外力矩方向垂直的動量矩,轉(zhuǎn)子軸的空間方位不斷地發(fā)生改變。由于外力矩的主要形式為重力偏心力矩,所以產(chǎn)生的力矩作用主要有2種情況:一種為軸向偏心力矩,在轉(zhuǎn)子軸坐標(biāo)系內(nèi)相對轉(zhuǎn)子幾何中心的作用方向不發(fā)生改變;另一種為轉(zhuǎn)子徑向偏心力矩,由于轉(zhuǎn)子高速旋轉(zhuǎn),偏心力矩的大小和方向不斷發(fā)生變化,產(chǎn)生的動量矩矢量也不斷變化方向。對轉(zhuǎn)子動力學(xué)模型進行數(shù)值求解,通過給定不同偏心距離以分析轉(zhuǎn)子定向方位的變化規(guī)律及特點。
圖3所示為轉(zhuǎn)子軸軸向偏心距不同條件下的水平方向偏轉(zhuǎn)角度ψ的變化規(guī)律。結(jié)果表明,軸向偏心距ex為1mm時,轉(zhuǎn)子軸便發(fā)生明顯的偏轉(zhuǎn),從慣導(dǎo)陀螺啟動到炮彈落地的整個過程,轉(zhuǎn)子在水平方向的偏轉(zhuǎn)為0~4.15°;當(dāng)軸向偏心距ex=-1mm時,偏轉(zhuǎn)范圍為0~4.21°;軸向偏心距ex=2mm時,轉(zhuǎn)子軸在水平方向偏轉(zhuǎn)范圍為0~16.48°;軸向偏心距ex=-2mm時,偏轉(zhuǎn)范圍為0~16.85°。

圖3 軸向偏心對轉(zhuǎn)子水平方向轉(zhuǎn)動角度的影響
圖4 所示為不同軸向偏心距條件下的俯仰角θ的變化規(guī)律。可以看出,轉(zhuǎn)子軸在俯仰方向產(chǎn)生明顯的偏轉(zhuǎn)。轉(zhuǎn)子軸向偏心相對幾何中心在轉(zhuǎn)子軸正方向時轉(zhuǎn)子向下偏轉(zhuǎn),相反則向上偏轉(zhuǎn)。當(dāng)偏心距離ex=1mm時,轉(zhuǎn)子軸向下偏轉(zhuǎn),偏轉(zhuǎn)0~-1°;ex=2mm時,偏轉(zhuǎn)角度為0~-2°;當(dāng)軸向偏心距ex=-1mm時,轉(zhuǎn)子軸向上偏轉(zhuǎn),偏轉(zhuǎn)角度為0~1°,ex=-2mm時,偏轉(zhuǎn)角度為0~2°。
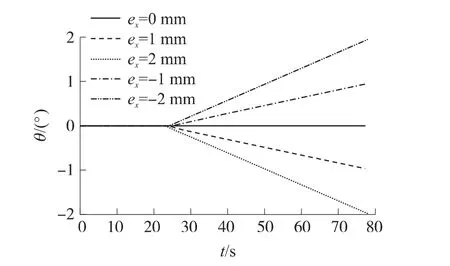
圖4 軸向偏心對轉(zhuǎn)子垂直方向轉(zhuǎn)動角度的影響
在進行轉(zhuǎn)子軸徑向偏心對轉(zhuǎn)子定向性影響分析時,轉(zhuǎn)子軸坐標(biāo)選定y軸方向或z軸方向都具有一般性。選定對y軸徑向偏心進行仿真,結(jié)果表明,y軸徑向偏心對轉(zhuǎn)子定向性的改變并不顯著,當(dāng)y軸徑向偏心距ey=1mm時,轉(zhuǎn)子側(cè)向偏轉(zhuǎn)角度約為0~0.2°,如圖5所示。
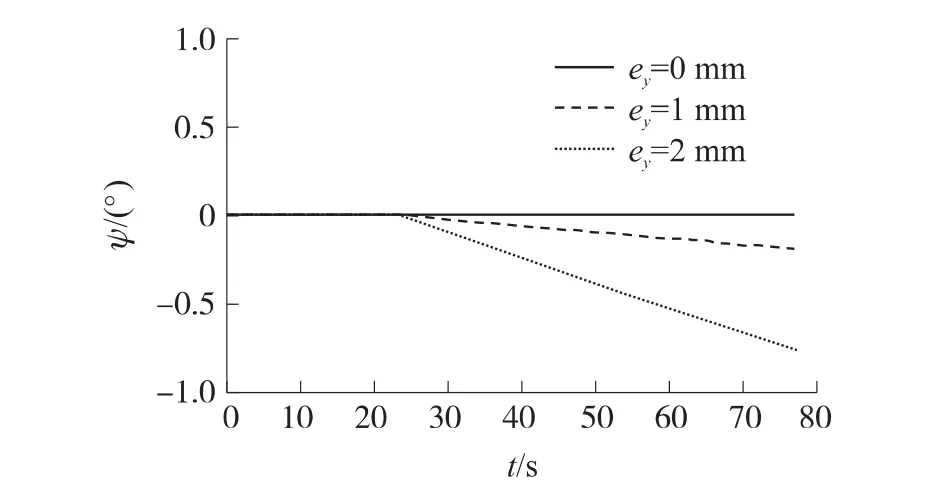
圖5 徑向偏心對轉(zhuǎn)子水平方向轉(zhuǎn)動角度的影響
俯仰方向角度偏轉(zhuǎn)曲線形式接近具有確定周期和幅值的簡諧曲線,但其偏轉(zhuǎn)角度平均并不為零。當(dāng)偏心距在相對幾何中心相反方向時,轉(zhuǎn)子偏轉(zhuǎn)方向相反,平均偏轉(zhuǎn)角度θe約為0~0.04°,如圖6所示。
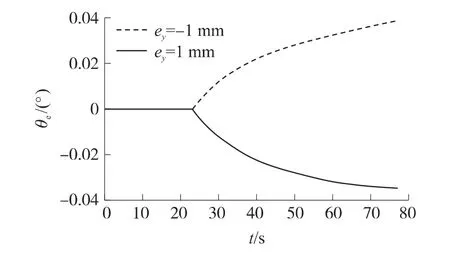
圖6 徑向偏心對轉(zhuǎn)子垂直方向角度變化的平均作用
因此,質(zhì)量偏心的轉(zhuǎn)子在重力矩的作用下可產(chǎn)生空間中的進動運動。軸向偏心對轉(zhuǎn)子進動作用明顯,進動角度與偏心距離成正比例關(guān)系。徑向偏心隨轉(zhuǎn)子旋轉(zhuǎn),所產(chǎn)生的動量矩矢量也同時隨之改變,轉(zhuǎn)子進動角速度呈周期性變化,但產(chǎn)生平均不為零的進動角度,表現(xiàn)為空間中的緩慢轉(zhuǎn)動,該結(jié)果可解釋慣導(dǎo)陀螺漂移現(xiàn)象。
該型號末制導(dǎo)炮彈零漂數(shù)據(jù)為15s時間內(nèi)水平方向漂移為-1.3°~0.4°,鉛垂方向的漂移為-0.5°~-2.3°。因此,根據(jù)數(shù)值仿真結(jié)果分析,轉(zhuǎn)子在x軸、y軸、z軸存在偏心情況下,仿真結(jié)果是可以解釋轉(zhuǎn)子漂移值的。
3 陀螺轉(zhuǎn)子質(zhì)量偏心對外框擺動角度的影響
陀螺轉(zhuǎn)子空間方位的改變,最本質(zhì)的是改變了內(nèi)、外框架的擺動角度。由于控制指令的發(fā)出取決于外框架的偏轉(zhuǎn),當(dāng)轉(zhuǎn)子質(zhì)心偏離幾何中心而導(dǎo)致轉(zhuǎn)子進動運動時,外框擺動角中則包含了轉(zhuǎn)子進動角度因素。
通過對轉(zhuǎn)子空間運動狀態(tài)的數(shù)值計算,可以確定任意時刻轉(zhuǎn)子軸的空間方位,利用式(8)求解外框擺動角。圖7為轉(zhuǎn)子存在軸向偏心與不存在軸向偏心條件下的慣導(dǎo)陀螺外框擺動角曲線(局部)。圖8為轉(zhuǎn)子存在徑向偏心與不存在徑向偏心條件下的慣導(dǎo)陀螺外框擺動角曲線(局部)。
圖7、圖8中的差異充分表明,轉(zhuǎn)子質(zhì)量偏心導(dǎo)致陀螺外框擺動角的變化,改變了慣導(dǎo)控制舵片指令生成時機,表現(xiàn)為慣導(dǎo)飛行時超前或滯后的舵面偏轉(zhuǎn)。這使得末制導(dǎo)炮彈控制力和控制力矩不再相對彈體正上方或正下方對稱,對末制導(dǎo)炮彈的彈道性能產(chǎn)生影響。

圖7 軸向偏心對外框擺動角的影響
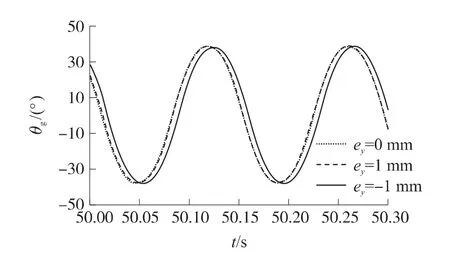
圖8 徑向偏心對外框擺動角的影響
4 陀螺轉(zhuǎn)子質(zhì)量偏心對彈道性能的影響分析
末制導(dǎo)炮彈射程、側(cè)偏、落角等參數(shù)是末制導(dǎo)炮彈在彈道設(shè)計時主要考慮的參數(shù)。初始段、無控段以及慣導(dǎo)飛行階段結(jié)束時,彈體激光制導(dǎo)陀螺啟動,進入末段導(dǎo)引段,控制系統(tǒng)導(dǎo)引彈體攻擊目標(biāo),若飛行距離過小或者側(cè)偏過大都將導(dǎo)致彈體不能按預(yù)定目標(biāo)飛抵捕獲區(qū)域,導(dǎo)致失去目標(biāo)。因此慣導(dǎo)飛行階段的精度控制對末端導(dǎo)引階段打擊精度影響很大。根據(jù)末制導(dǎo)炮彈彈道方程,結(jié)合慣導(dǎo)陀螺運動狀態(tài)方程,對末制導(dǎo)炮彈彈道特性進行數(shù)值仿真。針對轉(zhuǎn)子軸在3個方向上的偏心距導(dǎo)致彈道特性的變化分別進行仿真計算。
4.1 軸向偏心對彈道特性的影響
對轉(zhuǎn)子軸向偏心距分別取ex=2mm,1mm,0mm,-1mm,-2mm時的名義彈道進行仿真。不同條件下炮彈落點計算數(shù)據(jù)如表1所示。
從表1中數(shù)據(jù)可以發(fā)現(xiàn),轉(zhuǎn)子軸向偏心對名義彈道落點影響很大。當(dāng)軸向偏心距ex=1mm時,射程X減小49m,側(cè)偏Z變化約125.18m;當(dāng)ex=2mm時,射程X減小114m,側(cè)偏Z變化約488.38m;當(dāng)ex=-1mm時,射程X增加61m,側(cè)偏Z變化約123.18m;ex=-2mm時,射程X增加101m,側(cè)偏Z變化約500.02m。當(dāng)軸向偏心距在轉(zhuǎn)子軸正方向時射程會相應(yīng)減小,而軸向偏心距在轉(zhuǎn)子軸負(fù)方向時射程會相應(yīng)增加。在表1計算范圍內(nèi),射程X變化215m;飛行時間t、落速v、落角θ變化不大;側(cè)偏Z變化規(guī)律有所不同,只要軸向偏心距存在,不論是正、負(fù)方向,偏心距離絕對值相等時會產(chǎn)生大約一致的變化。

表1 軸向偏心對名義彈道落點諸元的影響
4.2 徑向偏心對彈道特性的影響
對轉(zhuǎn)子y軸徑向偏心距分別取ey=2mm,1mm,0mm,-1mm,-2mm時的名義彈道進行仿真。不同條件下炮彈落點計算數(shù)據(jù)如表2、表3所示。
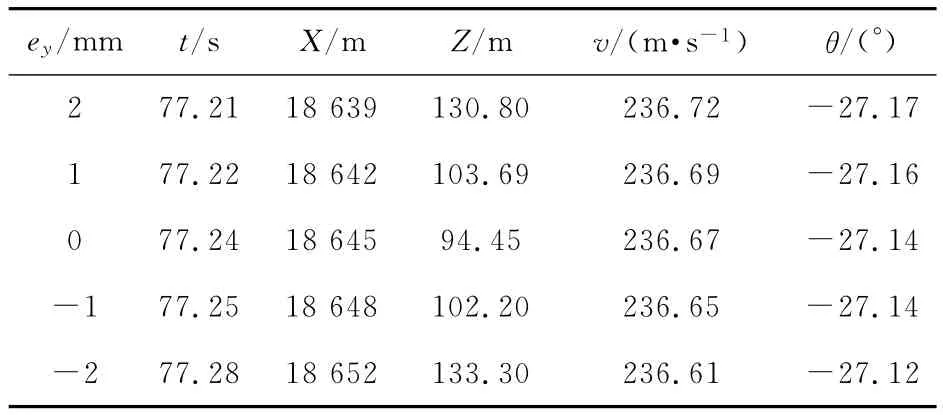
表2 y軸徑向偏心對名義彈道落點諸元的影響

表3 z軸徑向偏心對名義彈道落點諸元的影響
從表2中數(shù)據(jù)可以發(fā)現(xiàn),轉(zhuǎn)子軸y軸徑向偏心的存在對末制導(dǎo)炮彈名義彈道落點有一定的影響,且具有一定的規(guī)律性,即y軸徑向偏心由正到負(fù)變化時,射程變化趨勢為增大,射程變化約13m;對側(cè)偏變化也有一定的影響,且隨偏心距增大而增大。
從表3中數(shù)據(jù)可以發(fā)現(xiàn),轉(zhuǎn)子軸z軸徑向偏心的存在對末制導(dǎo)炮彈名義彈道落點有一定的影響,比y軸徑向偏心的影響偏大,但同樣具有一定的規(guī)律性。z軸徑向偏心ez由正到負(fù)變化時,射程變化趨勢為不斷減小,射程變化約96m;側(cè)偏變化隨偏心距增大而增大。對比表1和表2、表3,軸向偏心相比徑向偏心對彈道特性影響大,轉(zhuǎn)子軸z軸方向徑向偏心距離對彈道特性的影響比y軸徑向偏心距離對彈道特性的影響大,主要表現(xiàn)在射程變化以及側(cè)偏的變化。
因此,慣導(dǎo)陀螺轉(zhuǎn)子質(zhì)量偏心對末制導(dǎo)炮彈空間飛行的彈道諸元影響很大,為保證足夠的射擊精度,必須對轉(zhuǎn)子質(zhì)量偏心進行控制,以減少由于轉(zhuǎn)子進動帶來的影響。
本文對轉(zhuǎn)子質(zhì)心偏離幾何中心時的運動進行了數(shù)值仿真,并分析其對慣導(dǎo)飛行控制過程以及末制導(dǎo)炮彈彈道特性影響的特點,得出了以下結(jié)論:
①存在質(zhì)量偏心的轉(zhuǎn)子在重力矩的作用下失去慣性空間中的定軸特性,表現(xiàn)為陀螺漂移運動。其中軸向偏心對陀螺轉(zhuǎn)子運動的作用明顯,根本原因是重力矩不隨轉(zhuǎn)子旋轉(zhuǎn)而改變方向;而徑向偏心對陀螺漂移作用并不明顯,重力矩方向隨轉(zhuǎn)子旋轉(zhuǎn)而不斷改變,但轉(zhuǎn)子受重力矩作用的平均值不為零。
②軸對稱轉(zhuǎn)子質(zhì)量偏心使轉(zhuǎn)子發(fā)生漂移,改變了陀螺外框角度偏轉(zhuǎn)信號的變化規(guī)律,對舵片控制信號的形成造成超前或滯后的影響。
③軸向偏心對轉(zhuǎn)子水平或垂直方向偏轉(zhuǎn)角度貢獻較大,對射程和側(cè)偏改變很大。徑向偏心對轉(zhuǎn)子水平或垂直方向偏轉(zhuǎn)角度貢獻較小,對射程和側(cè)偏產(chǎn)生一定的影響。若要保證射擊精度,必須減小陀螺裝配誤差。
5 結(jié)束語
本文通過建立轉(zhuǎn)子運動狀態(tài)方程,分析了轉(zhuǎn)子定向軸變化對慣導(dǎo)飛行控制的影響,結(jié)合末制導(dǎo)炮彈外彈道模型,進行了數(shù)值仿真,并分別研究了轉(zhuǎn)子軸向偏心和徑向偏心對彈道特性的影響。為提高末制導(dǎo)炮彈射擊精度,必須減少陀螺轉(zhuǎn)子漂移角度,采取提高陀螺安裝準(zhǔn)確性的有效措施,也為研制新型末制導(dǎo)炮彈時陀螺部件的設(shè)計提供理論支持。
[1]宋衛(wèi)東,張進忠.慣導(dǎo)陀螺零漂對末制導(dǎo)炮彈彈道性能的影響[J].南京理工大學(xué)學(xué)報,2010,34(2):162-165.SONG Wei-dong,ZHANG Jin-zhong.Influence of zero drift of inertial guide gyro on trajectory characteristics of terminal guide shell[J].Journal of Nanjing University of Science and Technology,2010,34(2):162-165.(in Chinese)
[2]以光衢.陀螺理論與應(yīng)用[M].北京:北京航空航天大學(xué)出版社,1990.YI Guang-qu.The theory and applications of gyro[M].Beijing:Beijing University of Aeronautics and Astronautics Press,1990.(in Chinese)
[3]劉炳辰,宋衛(wèi)東.某型末制導(dǎo)炮彈慣導(dǎo)陀螺動力學(xué)分析與仿真[J].河北大學(xué)學(xué)報,2011,31(1):602-606.LIU Bing-chen,SONG Wei-dong.Simulation and dynamic analysis of terminal guide projectile’inertial guide gyro[J].Journal of Hebei University,2011,31(1):602-606.(in Chinese)
[4]劉延柱,薛紜.徑向質(zhì)量偏心的自由轉(zhuǎn)子陀螺的漂移運動[J].應(yīng)用數(shù)學(xué)和力學(xué),2004,25(7):718-722.LIU Yan-zhu,XUE Yun.Drift motion of free-rotor gyroscope with radial mass-unbalance[J].Applied Mathematics and Mechanics,2004,25(7):718-722.(in Chinese)

