導引頭量測誤差對落角約束最優制導律制導精度的影響

王 輝，林德福，王延東

（1.北京理工大學 宇航學院，北京100081；2.中國科學院 長春光學精密機械與物理研究所，長春130033）

隨著現代戰爭形式的變化及精確制導技術的快速發展，在實現對敵方地面高價值目標精確攻擊的同時，對末端攻擊角度也提出了約束，如對裝甲目標的掠頂攻擊、對敵方艦船的掠海－俯沖攻擊、航路點規劃等。同時，很多戰斗部的毀傷效能也與制導精度及末端攻擊角度密切相關，從頂部以近似垂直的角度進行攻擊可以達到更大的毀傷效果［1－2］。

傳統上，人們基于線性化的制導模型已經提出了僅帶落點約束、同時帶落點和落角約束的最優制導律［2－4］。在彈目視線角為小角度假設下，可以將上述制導律簡化成導彈加速度指令與彈目相對速度、彈目視線角、彈目視線角速度以及導彈剩余飛行時間的表達式，其中，彈目視線角速度為核心物理量，可以由平臺或動力陀螺導引頭直接測得［2－5］。簡化后的制導律表達形式簡單，易于工程實現。比例導引即為帶落點約束的最優制導律的工程簡化形式，在此基礎上發展了若干衍生形式，如增強型比例導引、積分比例導引、近似積分比例導引等［6－9］。而習慣上，一般將帶落點和落角約束的最優制導律簡稱為落角約束最優制導律。落角約束最優制導律是近幾年的研究熱點之一，相關的研究成果較多，如文獻［1－5，10－13］等。

本文僅研究對地攻擊的擴展落角約束最優制導律制導精度的一般性規律，根據文獻［2－6，10－13］的描述，制導精度分別用脫靶量和落角誤差表示。

1 擴展的落角約束最優制導律

傳統的對固定目標最優的落角約束制導律表達式為［2］

式中：vr為彈目相對速度；ac為導彈加速度指令；q，分別為彈目視線角和角速度；qf為彈道終端期望落角；tgo＝tf－t，為剩余飛行時間，tf為制導時間。

根據文獻［1］的研究成果，在利用最優控制理論推導制導律時，將控制權函數由1擴展為1／（n≥0），則引入參數n后的擴展落角約束最優制導律表達式為

比較式（1）、式（2）可以看出，二者的導航系數之比由4∶2擴展為2（n＋2）∶（n＋1）（n＋2）。

為了表述方便，文中將擴展的落角約束最優制導律簡寫成EOGLIAC（extended optimal guidance law with impact angle constraint）。

2 導引頭量測誤差及制導動力學

2.1 制導動力學

對一個具有實際意義的制導系統，制導動力學是必須要考慮的內容，這其中包括導引頭動力學、制導濾波器、駕駛儀動力學等。這些動力學既可能是高階的，也可能是低階的，這取決于建模的準確性及系統的需求。如對常規的兩框平臺導引頭，用二階或三階環節來描述是合適的；對過載駕駛儀，工程上常用的是經典兩回路、三回路駕駛儀或其變型，用二階或三階環節來描述也是合適的。上述導引頭和駕駛儀模型都沒有考慮慣性測量器件、濾波器、舵機等硬件動力學，一旦引入額外的硬件動力學，其階數可能達到10階、11階。

在做制導系統精度分析時，若直接引入高階的導引頭和駕駛儀動力學模型，由于可變參數較多，很難得出通用性的結論。因此，為了便于理論研究、簡化分析過程，通常將導引頭和駕駛儀動力學簡化成一階或二階環節來研究［2－8，10－13］。

2.2 導引頭量測誤差

導引頭量測誤差包括確定性誤差和不確定性誤差兩類。對EOGLIAC制導系統，導引頭不確定性量測誤差主要是指視線角速率誤差和視線角誤差Δq以及初始方向誤差（本文暫不考慮）；不確定性誤差主要是指導引頭量測噪聲，本文僅考慮導引頭探測器角噪聲，相關模型可參考文獻［2，5－6］，此處不再贅述。

3 導引頭量測誤差輸入下的EOGLIAC制導系統

3.1 EOGLIAC制導系統模型的建立

根據式（2），引入導引頭零位誤差、探測器角噪聲的EOGLIAC制導系統如圖1所示。圖中，Δq分別為導引頭彈目視線角速率零位誤差、彈目視線角零位誤差；ua表示輸入的探測器角噪聲；K2a為對應的噪聲功率譜密度，單位為rad2／（rad／s）；θ為彈道傾角；y′miss，θmiss分別為脫靶量和落角誤差；s為拉普拉斯算子；Th，Ta和Tg分別表示導引頭、駕駛儀和制導系統時間常數，其中，Tg＝Th＋Ta。

在對地攻擊時，EOGLIAC又可表示成：

由式（3）可以看出，彈道傾角θ追蹤彈目視線角q，在彈道末端θ（tf）與qf近似相等［12－13］，其中，tf為彈道的終端時刻。同時，導彈最終攻擊目標時的有效角度是終端彈道傾角而非彈目視線角，彈道傾角比彈目視線角更具工程意義。因此，落角誤差可根據θ（tf）－qf來計算［5，12］。

導引頭和駕駛儀均為一階環節，分別為1／（Ths＋1），1／（Tas＋1）。假設導引頭和駕駛儀總滯后時間常數為Tg，改變導引頭和駕駛儀動力學時間常數在總滯后時間常數中的權重，即可研究導引頭和駕駛儀動力學的快速性比值對脫靶量的影響。表1給出了總滯后時間常數為Tg，Th／Ta分別為1／5，1／2，1，2，5時的動力學分配情況。

圖1 3種誤差輸入下的落角約束最優制導律制導系統結構圖

表1 導引頭和駕駛儀動力學不同選取狀態

3.2 無量綱的EOGLIAC 伴隨系統

定義無量綱時間＝t／Tg，則＝s／Tg，＝tf／Tg－，其中，tf／Tg表示無量綱末導時間。經過無量綱和伴隨模型變換，得到圖2、圖3所示的無量綱脫靶量和無量綱落角誤差伴隨模型。圖中，k1＝分別表示彈目視線角及角速率零位誤差、探測器角噪聲引起的無量綱脫靶量；ymiss｜Δq，ymiss｜Δ，σmiss｜a為常規脫靶量；相應地｜Δq｜Δ，｜a為無量綱落角誤差；θmiss｜Δq，θmiss｜Δ，σθmiss｜a為常規落角誤差。圖2、圖3中的（）2表示對當前信號進行平方示對當前信號取平方根。

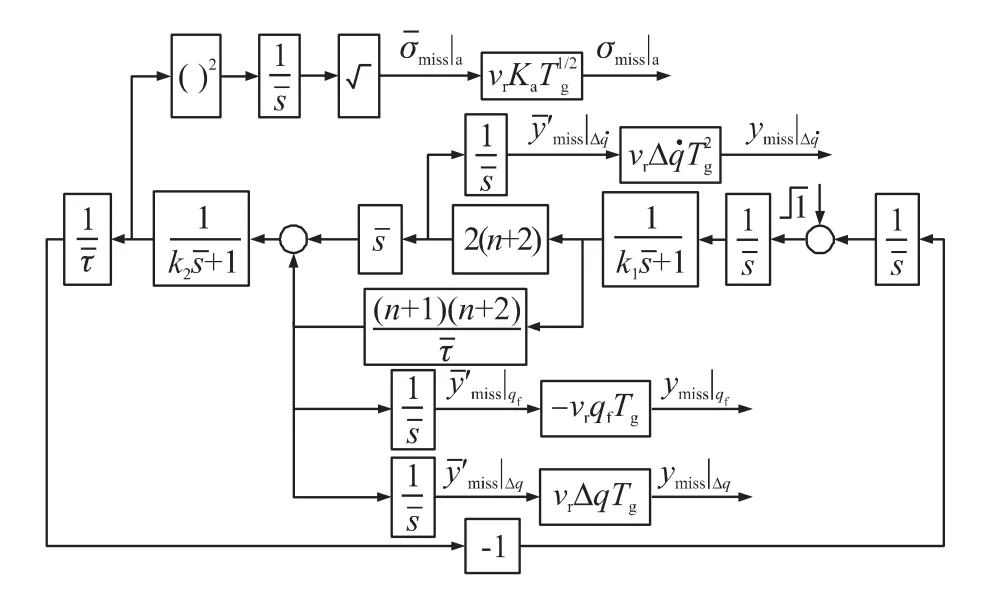
圖2 脫靶量伴隨系統結構圖

由圖2、圖3的結果可以看出，彈目視線角零位誤差引起的脫靶量與vr，Δq，Tg成正比，落角誤差與Δq成正比；彈目視線角速率零位誤差引起的脫靶量與vr，，T2g成正比，落角誤差與，Tg成正比；探測器噪聲引起的脫靶量與Ka，vr，成正比；落角誤差與Ka成正比，與成反比。

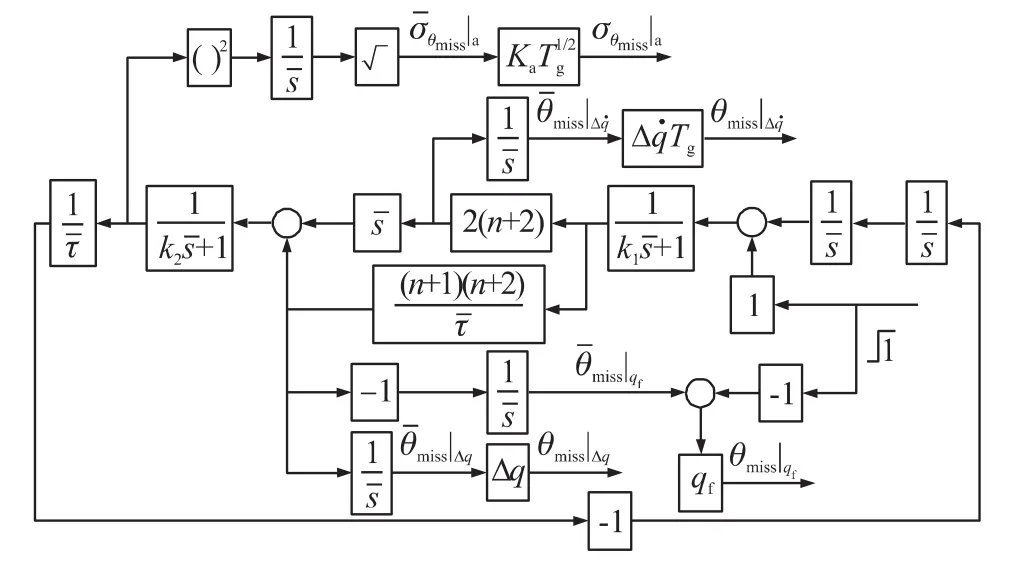
圖3 落角誤差伴隨系統結構圖

由上面的分析可知，無量綱化前制導系統的可變參數有n，vr，Δq，，，Th，Ta，tf等8個，無量綱化后只有n，Th／Ta，tf／Tg等3個，因此，通過無量綱化有效地減少了可變參數，為后續脫靶量和落角誤差的研究創造了方便。

4 EOGLIAC制導系統無量綱脫靶量和落角誤差分析

根據制導系統的常規模型（圖1）及無量綱伴隨模型（圖2、圖3），對上述導引頭量測誤差作用下的位置和落角誤差進行研究。在下面的仿真結果中，圖的縱軸為各誤差對應的無量綱脫靶量和落角誤差，虛－實線表示伴隨模型結果，離散圓點表示常規模型結果。

4.1 導引頭視線角零位誤差引起的無量綱脫靶量和落角誤差分析

Δq作用下的無量綱脫靶量和落角誤差如圖4、圖5所示。在圖4（a）、圖5（a）中，Th／Ta取為2；在圖4（b）、圖4（c）及圖5（b）、圖5（c）中，Th／Ta的取值規律如表1所示。

由仿真結果可以看出：對不同的指數n及不同的導引頭和駕駛儀權狀態，當tf／Tg≈15時，Δq引起的無量綱脫靶量收斂到零附近，無量綱落角誤差收斂到－1附近；隨著指數n的增大及導引頭動力學時間常數的增加，無量綱脫靶量和落角誤差振蕩趨勢加劇，峰值加大；與駕駛儀動力學相比，增加導引頭的快速性能更有效地減少Δq對制導精度的影響。

下面對落角誤差收斂到－1進行分析。由式（2）可知，落角約束項為（q－qf）／tgo，彈目視線角q追蹤終端約束角qf；當彈目視線角有零位誤差Δq時，落角約束項實際變為［q－（qf－Δq）］／tgo，彈目視線角q實際追蹤的是qf－Δq。若末導時間足夠長，在彈道末端，θf＝qf－Δq，則無量綱落角誤差為（θfqf）／Δq＝－Δq／Δq＝－1，即上述仿真結果與理論分析是一致的。

4.2 導引頭視線角速率零位誤差引起的無量綱脫靶量和落角誤差分析

圖4 導引頭視線角零位誤差引起的無量綱脫靶量

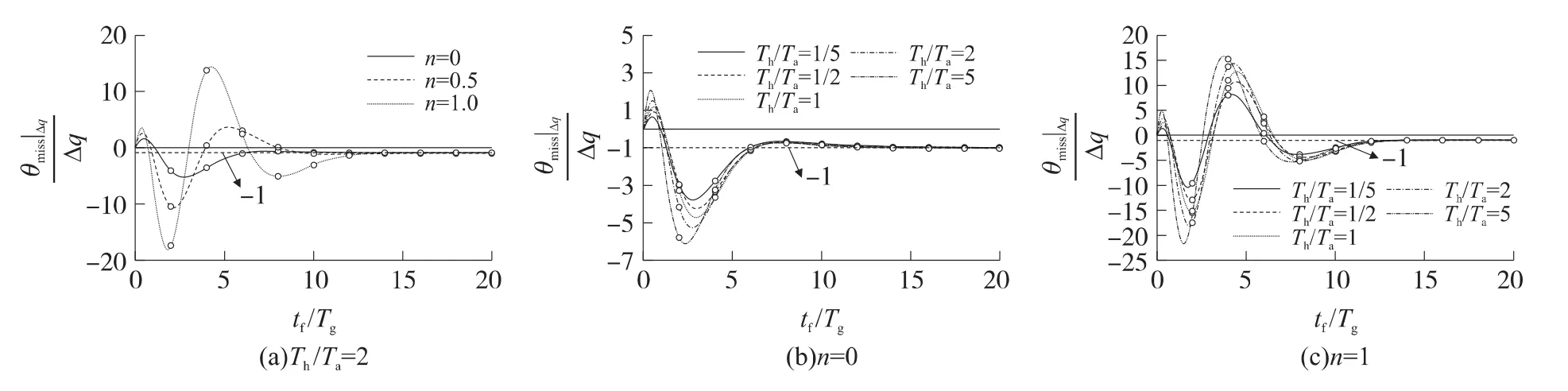
圖5 導引頭視線角零位誤差引起的無量綱落角誤差

圖6 導引頭視線角速率零位誤差引起的無量綱脫靶量

圖7 導引頭視線角速率零位誤差引起的無量綱落角誤差

4.3 探測器噪聲引起的無量綱脫靶量和落角誤差分析

圖8 、圖9分別給出了探測器角噪聲作用下的無量綱脫靶量和落角誤差隨tf／Tg和指數n（n∈［－0.5，1］）的變化曲線。由此可以看出：探測器角噪聲引起的無量綱脫靶量和落角誤差并不隨tf／Tg的增大而趨向于零；當tf大于Tg的10倍時，脫靶量和落角誤差達到穩態值，且隨著指數n的增大，該穩態值顯著增大。圖8（b）、8（c），圖9（b）、9（c）的仿真結果表明，在Tg一定及脫靶量和落角誤差達到穩態值（tf／Tg＝15）的情況下，隨著導引頭和駕駛儀時間常數比值的變化，當導引頭與駕駛儀響應速度一致時，系統無量綱脫靶量和落角誤差均達到最大值。由于探測器噪聲引起的脫靶量與T1／2g成正比，落角誤差與T1／2g成反比，因此，在制導系統滯后時間常數一定的情況下，為了盡量降低探測器角噪聲對制導精度的影響，指數n不應選得過大［2，6］。

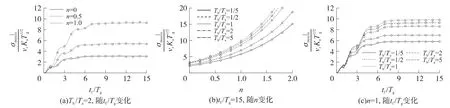
圖8 導引頭探測器噪聲引起的無量綱脫靶量

圖9 導引頭探測器噪聲引起的無量綱落角誤差

4.4 指數n的工程選取

根據式（2）中導航系數與參數n的關系式可知，指數n與導航系數一一對應，因此確定了指數n，也就確定了導航系數。指數n大時有利于消除導引頭視線角速率零位誤差引起的脫靶量，也能加快制導系統響應；但大的n會放大探測器角噪聲引起的制導誤差，也會使導引頭視線角零位誤差、落角約束、初始方向誤差等引起的制導誤差振蕩加劇，收斂時間變長，同時在彈道初始段也容易造成過載飽和［6］。因此，制導系統工程師應根據導彈過載能力、各種誤差引起的制導誤差與總體技術指標間的關系，綜合確定n的取值范圍。

若以比例導引的導航系數N的最大取值6為上界，以傳統的落角約束最優制導律的位置項導航系數4為下界，則可確定擴展的落角約束最優制導律的位置項導航系數的取值范圍，進而可確定指數n的取值范圍。根據2（n＋2）∈［4，6］，則指數n可取在0～1之間。

5 結論

本文以擴展的落角約束最優制導律為研究對象，針對地面固定目標，分別研究導引頭視線角速率零位誤差、視線角零位誤差和探測器角噪聲對制導精度的影響。研究結果表明：

①當末導時間達到制導系統滯后時間常數的15倍左右時，可以消除導引頭視線角零位誤差對脫靶量的影響。此時，導引頭視線角零位誤差引起的落角誤差收斂到穩態值－1。

②大的指數n有利于消除導引頭視線角速率零位誤差對脫靶量和落角誤差的影響。

③在導引頭視線角速率和視線角零位誤差作用下，提高導引頭的響應比提高駕駛儀的響應更有利于降低制導誤差。

④探測器角噪聲引起的制導誤差并不隨著末導時間的增大而趨向于零，而是隨著末導時間的增大收斂到穩態值，且指數n越大，穩態制導誤差越大。因此，為了盡量降低探測器角噪聲對制導精度的影響，指數n不應選得過大。

⑤參考比例導引及傳統的落角約束最優制導律有效導航比的選擇范圍，建議指數n選在在0～1之間。

本文的研究方法同樣適用于復雜的制導動力學模型，同時，文中的研究僅針對地面固定目標。若研究空中機動目標，需將目標機動補償項引入到制導律中。

［1］OHLMEYER E J，PHILLIPS C A.Generalized vector explicit guidance［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）：261－268.

［2］ZARCHAN P.Tactical and strategic missile guidance，5th edition［M］.Virginia：AIAA Inc，2007：31－50，541－569.

［3］常超，林德福，祁載康，等.帶落點和落角約束的最優末制導律研究［J］.北京理工大學學報，2009，29（3）：233－239.CHANG Chao，LIN De－fu，QI Zai－kang，et al.Study on the optimal terminal guidance law with interception and impact angle［J］.Journal of Beijing Institute of Technology，2009，29（3）：233－239.（in Chinese）

［4］WANG H，LIN D F，CHENG Z X.Time－to－go weighted optimal trajectory shaping guidance law［J］.Journal of Beijing Institute of Technology，2011，20（3）：317－323.

［5］劉大衛，夏群利，崔瑩瑩，等.具有終端位置和角度約束的廣義落角約束最優制導律［J］.北京理工大學學報，2011，31（12）：1 408－1 413.LIU Da－wei，XIA Qun－li，CUI Ying－ying，et al.Generalized trajectory shaping guidance law with both impact position and angle constrains［J］.Journal of Beijing Institute of Technology，2011，31（12）：1 408－1 413.（in Chinese）

［6］GARNELL P.Guided weapon control systems［M］.Beijing：Beijing Institute of Technology Press，2003：297－364.

［7］王輝，林德福，祁載康，等.時變最優的增強型比例導引及其脫靶量解析研究［J］.紅外與激光工程，2013，42（3）：692－698.WANG Hui，LIN De－fu，QI Zai－kang，et al.Study of time－varying optimal augmented proportional navigation and miss distance closed－form solutions［J］.Infrared and Laser Engineering，2013，42（3）：692－698.（in Chinese）

［8］張宏，夏群力，祁載康，等.基于目標機動補償的增強型比例導引性能研究［J］.紅外與激光工程，2007，36（1）：82－87.ZHANG Hong，XIA Qu－li，QI Zai－kang，et al.Augmented proportional navigation with maneuvering target compensation［J］.Infrared and Laser Engineering，2007，36（1）：82－87.（in Chinese）

［9］PRASANNA H M，GHOSE D.Retro proportional navigation：a new guidance law for interception of high speed targets［J］.Journal of Guidance，Control，and Dynamics，2012，35（2）：377－386.

［10］BEN－ASHER J Z，YAESH I.Optimal guidance with reduced sensitivity to time－to－go estimation errors［J］.Journal of Guidance，Control，and Dynamics，1997，20（1）：158－163.

［11］BEN－ASHER J Z，YAESH I.Advances in missile guidance theory［M］.Virginia：AIAA Inc.，1998：25－88.

［12］RYOO C K，CHO H，TAHK M J.Optimal guidance laws with terminal impact angle constraint［J］.Journal of Guidance，Control，and Dynamics，2005，28（4）：724－732.

［13］RYOO C K，CHO H，TAHK M J.Closed－form solutions of optimal guidance with terminal impact angle constraint［C］／／Proceeding of IEEE International Conference on Control Application.Istanbul，Turkey：IEEE，2003：504－509.