淺談不定式極限

張石鳳

（云南大學旅游文化學院 信息科學與技術系，云南 麗江674100）

limα(x)=limβ(x)=0.

對于這種類型的未定式是非常重要的一種極限，求該類型的極限，通常用到洛必達法則。

定理1.1（洛必達法則） 若函數α(x)與β(x)滿足條件：

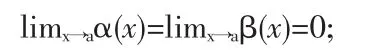
(2)在點 a的某去心領域內 α(x)與 β(x)可導，且 β'(x)≠0；

(3)limx→a存在（或為∞）

則 limx→a=limx→a

注：（1） 極限過程改為 x→a+,x→a-,x→∞,x→-∞,x→+∞ 有類似的結論。

（2）若 limx→a仍然滿足洛必達法則的條件，則可連續運用該法則，即:limx→a=limx→a

（3）若 limx→a不存在（不含∞）,不能斷言limx→a不存在。

在實際計算中，常常把該法則與等價變形、重要極限及等價無窮小代換等其他求極限的重要方法一起使用。

解：若用洛必達法則，分子分母分別求導得limx→0，該極限為振蕩不存在，故洛必達法則失效。實際上，可利用等價無窮小量代換 ln（1+x）∽x（x→0），得

limα(x)=limβ(x)=∞

定理2.1（洛必達法則） 若函數α(x)與β(x)滿足條件：

（1）limx→aα(x)=limx→aβ(x)=∞；

（2）在點 a 的某去心領域內 α(x)與 β(x)可導，且 β'(x)≠0；

（3）limx→a存在（或為 ∞）

則 limx→a=limx→a

該定理也有類似于定理1.1的注釋，定理1.1與定理1.2統稱為洛必達法則。

3 其它類型的不定式極限

不定式極限還有0·∞，∞-∞，1∞，∞0等類型。經過簡單變換，它們一般都可化為型或型的極限。

對于0·∞及∞-∞型不定式極限，經過適當的變化，即可將其化為型或的極限。

例 4 limx→0＋x ln x（0·∞）

對于該種類型的不定式極限，只要將其一除至分母，即可將其化為型或的極限。

對1∞，00，∞0等型不定式極限，可先化為以e為底的指數函數的極限，再利用指數函數的連續性，化為求指數部分的極限，而指數部分的極限，可化為型或的極限，再運用洛必達法則即可。

例 7 limx→0+χx（00）

解：limx→0+

χx=limx→0+eχlnx=e0=1.

4 總結

洛必達法則是解決不定式極限的很有效的方法。但必須注意的是，只有型和型不定式而且必須在符合洛必達法則的各項條件時才能直接使用洛必達法則。對于其他型不定式必須經過變換化為滿足條件的型和型不定式才能使用洛必達法則。有時還需要與其他求極限的方法結合使用。在求極限時，不必一一去驗證洛必達法則的各項條件，只要判斷是型和型不定式即可先用著洛必達法則，若求極限過程可進行下去，說明洛必達法則可以失效，若運用洛必達法則不能得出最后結果（極限不存在），這個時候說明洛必達法則失效，不能使用，不能說明該極限不存在，此時需要用別的辦法判斷極限是否存在。

［1］趙樹嫄．經濟應用數學基礎（一）微積分[M].3版.中國人民大學出版社.

［2］華東師范大學數學系編.數學分析:上冊[M].3版.高等教育出版社.