序列相似性網絡聚類與蛋白質家族劃分

時逢寬， 李煒疆

（1.江南大學 工業生物技術教育部重點實驗室，江蘇 無錫 214122；2.江南大學 生物工程學院，江蘇 無錫 214122）

隨著近年測序技術發展，蛋白質序列數據爆炸式增長。到目前為止，收錄信息資源最廣的蛋白質數據庫 Uniprot（http：//www.uniprot.org）中儲存了超過3 600萬條蛋白質序列。這些序列已知的蛋白質絕大部分的功能是未經實驗鑒定的，必須借助計算方法確定，而聚類方法尤其是近年引起關注的圖聚類方法，為從序列解讀蛋白質功能提供了一種高效途徑。

聚類方法實現蛋白質按功能分類是一個探索蛋白質同源關系的過程，通過序列相似性推斷具有共同祖先的蛋白質。實施蛋白質按功能聚類的第一步是獲取蛋白質之間功能聯系的描述的依據是序列間的相似性關系網絡（稱為關聯圖），兩兩比對相似性分數，這些分數通常可以利用BLAST[1]或FASTA[2]算法高效率地獲得。如果待分類蛋白質由集團特征明顯的類別組成，亦即同類蛋白質之間的序列相似性顯著高于不同類之間的相似性，則傳統的聚類法，例如層次聚類，既可方便快捷地實現分類。但是當蛋白質間的序列相似性很低，接近隨機漲落區域時，隨機成分（噪音）在相似性分數中所占比重越來越大，嚴重干擾聚類過程，一般的聚類方法就難以奏效，而圖聚類（Graph Clustering）則可以更好克服噪音干擾，揭示隱蔽的分類結構。

蛋白質相似性網絡通常表示為無向圖，圖中節點為蛋白質，節點之間的邊為序列相似性分數，從而將蛋白質相似性分類問題變換為利用圖論的圖聚類問題。例如，maximal clique方法通過尋找圖中節點之間相互完全連通的子圖尋找功能模塊[3]，但是蛋白質序列之間無法達到如此高的連接程度，因此只能找到少量的集團；MCL方法通過對相似性矩陣不斷交替使用expansion操作和inflation操作，直到矩陣不再變化為止，即為冪等矩陣，對應最后的聚類結果[4]，然而Paccanaro等人研究發現MCL算法很容易產生較很小的集團。作者采用的基于最優模塊度的圖聚類CD算法[5]，以模塊度作為衡量集團結構的強弱的指標，將聚類問題轉換為尋找模塊度最大的集團，以往的研究表明該算法能用極短時間獲得較高質量的聚類結果。本文主要研究：考察當數據關系極其復雜以及數據規模極不均勻時該算法的穩定性；通過不同方法構建鄰接矩陣對聚類結果的影響；如何在聚類起始預估最佳閾值范圍。

1 數據與方法

1.1 蛋白質序列及家族分類

由于研究內容與蛋白質功能有關，而Pfam蛋白質家族數據庫[6]是大量依據功能相關分類的集合。其中的Pfam-A的數據為專家審核維護集合，質量較好可靠性較高；Pfam-B則是利用自動算法劃分的未經過人工審核的數據集合。宗族（Clan）[6]是指根據序列相似性，功能相關或隱馬爾科夫模型（HMM）收錄于Pfam-A中的集合。蛋白質家族是指具有同源性結構域以及序列具有進化相關或者功能相似的蛋白質所形成的集群。家族內在結構上與功能上具有比較強的同源關系，而表現在序列方面則具有顯著的序列相似性。集團節點間連接的概率，家族內>家族間>宗族間。同一宗族內部家族成員之間關系與非同宗族相比較而言較為緊密，加大了數據的復雜度以及聚類難度。

蛋白質序列數據來自Pfam數據庫26.0版本中人工維護的可信度較高的Pfam-A中獲得，選擇Multiheme_cytos （CL0317）宗族[7]，包含 9 個家族成員，由于家族間具有一定的進化關系以及家族規模差異較大，該數據能較好的反應實際數據存在形式，本文使用該數據能有效的測試CD算法在家族間聯系較為緊密以及家族分歧較大時仍能表現較好的穩定性以及高效性。本宗族中其中一共包含2 210條序列，對于圖聚類算法而言，數據結構不均一將影響聚類結果的質量，作者采用的數據集家族內成員在規模上也有較大分歧極度不均一，目的以測試基于模塊度最優的CD算法表現。家族內成員的數目分布如表1所示。

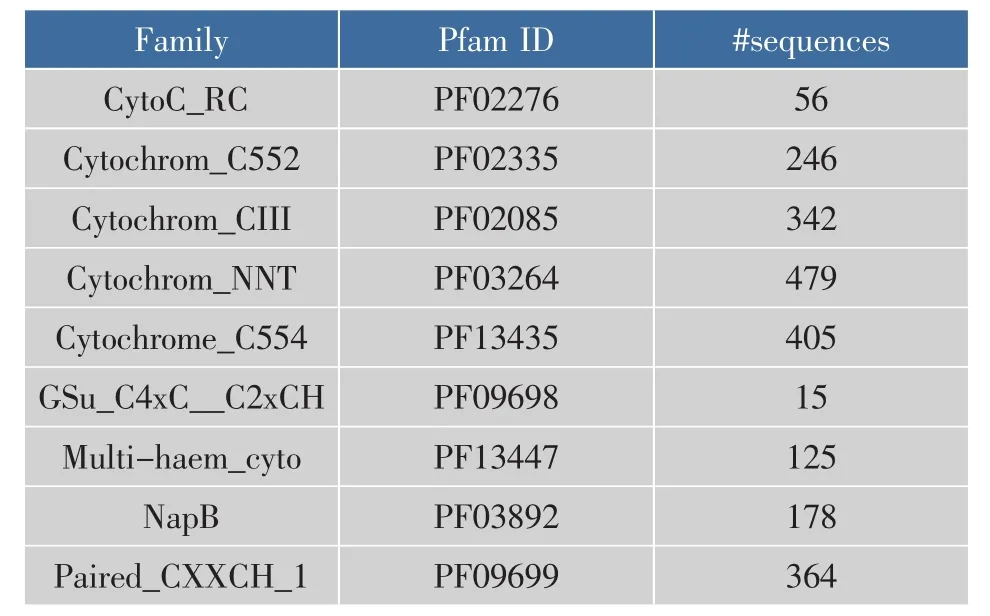
表 1 測試數據集（CL0317宗族）中的序列在各家族的分布Table 1 Distribution of sequences in each family in the tested dataset（CL0317）

其總數據、家族內與家族間的相似性分數分布情況如圖1所示。

圖1為本文采用的數據集的Score分布情況。由于采用BLAST計算相似性分數時，只報告相似性顯著的序列對（E＜10）。從數據分布情況可知家族內序列對相似性顯著比例較高序列之間連接緊密，相反家族間的結連接為稀疏，使得采用模塊度的圖聚類進行蛋白質分類成為可能。家族內相似性不顯著的序列對約占家族內總數據的30%，家族內的序列相似性分數分布的峰值處于30附近；不僅如此，來自不同家族間的序列相似性顯著的序列對約占19%，其Scores峰值也在30附近。這些不正確的序列關聯嚴重干擾聚類過程中序列的正確分類，例如簡單依據相似性距離的層次聚類。

圖1 家族內與家族間的相似性分數分布情況Fig.1 Distributions of sequence score between pairs of sequences.Note that the main parts of the distributions are in the fluctuation region with very low sequence score

圖2中的“點”為兩條序列節點之間有BLAST報告的，即序列之間相似性顯著。由于家族內成員之間相似性顯著所占比例大于家族間，從而形成圖中所示的塊狀結構，而由圖1中的家族間相似性顯著序列也占有一部分，從而導致圖2中家族之間的界限比較模糊，家族間相互聯系互相干擾使得聚類難度增大。

圖2 所有BLAST報告中序列之間相似性E-value＜10的稀疏結構圖Fig.2 Spy plot of the similarity between all sequence pairs reported by BLAST all-against-all search with E-value＜10.Each dot represents a significant match between the corresponding pair of sequences

1.2 算法簡介

圖聚類在最近幾年廣泛的應用于各個領域學科例如生物信息學、模式識別、社會社交等[8-17]，特別是采用網絡模塊度的圖聚類方法得到了更高的關注。模塊度是由Newman和Girvan[8-20]提出的用于衡量聚類結果中網絡集團結構特征強弱的指標，通過搜索使模塊度最大化的集團劃分，即可實現網絡節點的聚類，例如將蛋白質劃分為不同家族。模塊度最大化是NP困難問題，沒有快速精確求解方法，只能用近似方法尋求次優解。CD算法[5，20]是一種高效的模塊度最大化算法，在眾多實際應用問題中表現出良好性能，因而選作本文的圖聚類算法。

1.3 鄰接矩陣構造方法

蛋白質相似性網絡是基于序列之間相似性定義的，表示蛋白質之間的相似程度，通常是賦權圖，其中節點為蛋白質，邊的權重為利用BLAST獲得的序列兩兩比較的E-value（E值）或Score（S值）。當兩個序列的相似性臨近隨機漲落區域時，其BLAST報告的E或S分值就由隨機因素主導，從而逐漸失去了精確量化相似程度的意義，將這些分數直接輸入聚類算法就可能干擾聚類結果。因此在本文中，采用非賦權圖表示蛋白質相似性網絡，其中的邊僅表示存在相似關系而不包含程度信息，相應的鄰接矩陣由0和1構成。采用非賦權圖還可以顯著降低圖聚類的算法復雜度。

本文BLAST報告的E值和S值為基礎，采用閾值過濾方式構建鄰接矩陣，考察不同的閾值對聚類結果的影響，尋找最佳閾值。基于S值構建鄰接矩陣可以表示為

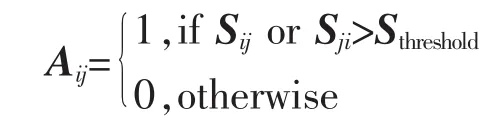
其中 i，j表示蛋白質；Aij為鄰接矩陣的 （i，j）元素，表示蛋白質i與j之間是否存在相似關系；Sij為蛋白質i與j之間的BLAST相似性分數；Sthreshold為給定的閾值。 由BLAST計算得到的相似性分數矩陣不是嚴格對稱的，亦即Sij與Sji有差異，對此我們采用取最大分數使其對稱化。

當以E值為基礎構建鄰接矩陣時，采用如下過濾方式

1.4 聚類結果與已知分類一致性的評估方法

聚類結果所對應的Q值反應了在給定聚類模型下，算法尋找最優解的能力。為了評價聚類結果與蛋白質家族分類的一致性，我們采用歸一化互信息 NMI（Normalized Mutual Information）描述聚類結果與目標分類的吻合程度，其定義為[23-24]

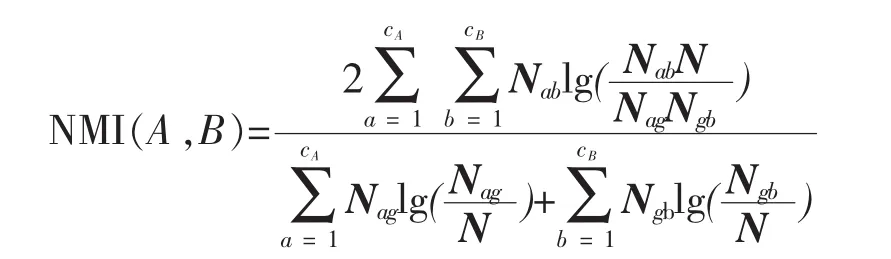
其中A表示蛋白質家族分類；B表示聚類結果；cA表示家族數；cB表示聚類結果的集團數；Nab表示家族a的成員中在聚類結果中劃分至集團b的數目；由Nab構成的矩陣稱為混淆矩陣（confusion matrix），刻畫了不同分類之間的相互關系。為家族a中蛋白質總數，為聚類結果中屬于集團b的蛋白質數目。

NMI的數值是介于0與1之間，越接近1則聚類結果與目標分類的一致性就越好，當NMI等于1時，實際分類與目標分類是完全等價的。

2 結果和討論

采用的圖聚類算法CD是隨機算法，每次運行得到的結果都略有差異，多次重復運算可以獲得更好的結果。為了獲得盡可能穩定的分類結果，在一次聚類計算中重復運行CD程序，一般說來，運算次數越多，以模塊度衡量的計算結果越好，當然需要的計算量也越大。在一定閾值下構建鄰接矩陣，測試了選取不同運算次數時算法穩定性的表現，結果見圖3。

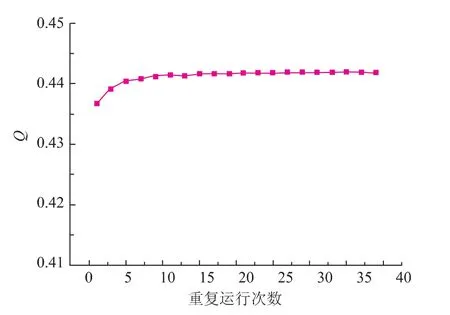
圖3 不同的重復運行次數與最優模塊度QFig.3 Best modularity （Q）values obtained in multiple runs of the CD algorithm with different replication numbers.The mean values and standard errors were calculated on 100 outputs of multiple runs

隨著運算次數的增加計算的次數大幅增加，Q值平均值增加，但是波動逐步減小，隨著運算次數的增加穩定性逐步增強，因此在合適的配置數下能減小算法隨機波動所導致的誤差，綜合考慮選擇相同情況下運算程序10次，然后取Q值最大時為最優解。

作者使用的CD算法通常不需要調整參數，只需將初始最大集團數目（nslots）設置為大于可能的最終分類數即可，CD算法在優化搜索過程中能夠自動縮減分類數至合適的數值。測試結果也表明當nslots足夠大時，聚類結果不依賴于nslots的具體取值，故固定選取nslots=100。

選取不同的閾值得到的鄰接矩陣也不同，進而影響最終聚類結果。對于數據集CL0317，采取多個閾值構建鄰接矩陣然后計算CD聚類，結果見圖4。圖中每個閾值對應的CD聚類均重復100次，考察算法的平均性能和穩定性。

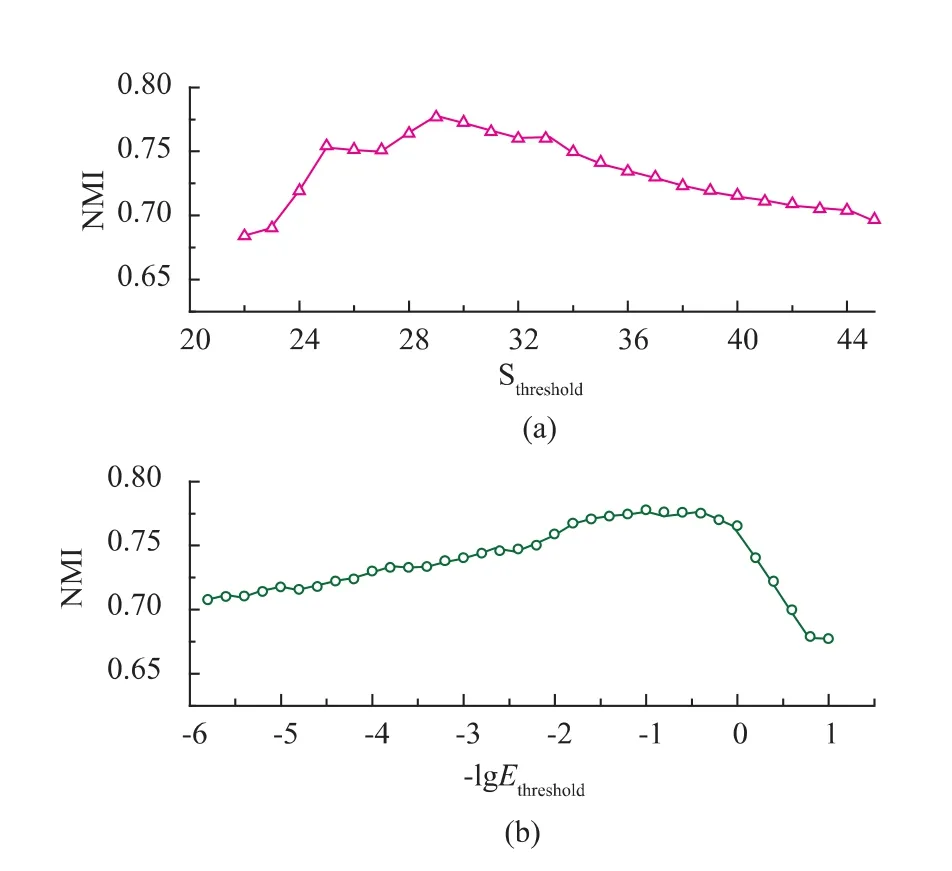
圖4 使用NMI衡量鄰接矩陣對聚類結果的影響Fig.4 Influence of the adjacency matrix on the clustering performance measured by normalized mutual information. The adjacency matrices are constructed by filtering A）similarity scores and B）E-values with varied thresholds.

由圖4可見，基于E值與基于S值得到的聚類性能沒有明顯差異。以S值構建鄰接矩陣時，最佳聚類結果在Sthreshold=29附近獲得，但是在Sthreshold=25～33這樣一個很寬的范圍內，平均NMI值起伏很小，表明聚類方法對于鄰接矩陣的適度寬容性。

當采用非常嚴格的相似性標準，即Sthreshold遠大于最佳閾值時，相似性圖中因隨機效應導致的錯誤連接大量減少，同時真實反映序列關聯的正確數據也被過濾掉，使得聚類依據不足從而性能明顯下降。相反，過于寬松的閾值（即Sthreshold很小）使得相似性圖中隨機連接大量增加進而降低聚類準確性。

當以E值為基礎構建鄰接矩陣時，結果是類似的，最佳聚類性能在lgEthreshold=-2～0較寬的范圍內達到。我們注意到，這樣的相似性標準比通常采用的BLAST 標準（E～10-5—10-2）寬松，說明此時的相似性圖中含有較多的隨機誤差數據，采用的聚類方法能夠滿意地從噪音數據中提取正確的分類信息。

采用Pfam數據庫中人工維護審核的Pfam-A數據庫中的一個宗族，由于宗族內的家族成員之間有著一定關系，與非宗族內的蛋白質數據相比聚類難度大。圖聚類中家族大小規模不均勻分或分歧度較高是聚類分析中比較難以聚類的情況，作者挑選這一宗族Paired_CXXCH_1家族有479條序列，小的GSu_C4xC__C2xCH家族只有15條序列，兩者相差數十倍，詳見表1，這樣的數據集是典型蛋白質家族關系，從而本實驗的結果更能說明利用序列相似性網絡基于模塊度的CD聚類算法的優良性能和通用性。

綜合結果可以發現，鄰接矩陣的構建方法對聚類結果有著較為密切聯系，并且使用基于模塊度的CD算法能夠有效的挖掘網絡內在的集團結構，并將有效信息從包含大量噪音的數據中提取出來。由于隨著構建鄰接矩陣采用的閾值限定的增強 （減弱）節點之間的聯系減少（增多），噪聲減少（增強），節點之間連接正確率增高（降低），導致圖聚類算法的可用信息逐步減少（增多）。閾值限定的增強導致節點之間的連接減少，形成大量的孤立點，從而算法無法判斷其所屬導致聚類結果下降；閾值限定的減弱導致節點之間的連接增多，有用信息量增加的同時引入大量的錯誤信息，正確數據淹沒在大量的噪聲中使得算法無法正確判斷分類信息。研究表明：盡管采用不同類型的相似性分數作為構建鄰接矩陣的閾值，CD算法仍能在較為寬松的閾值范圍內從包含大量噪聲的數據中識別出具有功能的集團結構，即只要輸入CD算法的鄰接矩陣包含有足夠多分類信息，該算法就可以獲得與實際結果一致性較高的聚類結果。而對于采用single-linkage層次聚類的聚類結果分析得到NMI數值為0.028，形成了巨大的一個集團與一些零散的小集團，相比采用CD算法的NMI值為0.778，結果明顯更加合理。通過分析表明CD圖聚類算法聚類結果最優閾值與圖1中總數據、家族內和家族間數據分布峰值是一致的，通過本文的研究使得聚類前對數據分布分析可以估計最佳閾值范圍。

由于家族內外的序列相似程度的高低差異，由圖1的相似性分布可知白質序列家族劃分不能簡單依據相似性進行蛋白質家族劃分。Pfam-A中的蛋白質家族為檢驗本實驗結果的準確性提供了數據支持，蛋白質之間的相似性分數可以通過BLAST進行一一比對獲得，采用不同的相似性數值構建相似性矩陣，矩陣節點之間的權重采用不同的相似分數，依據構建的相似性矩陣采用不同的閾值構建鄰接矩陣，本實驗重點研究不同的相似分數以及不同閾值構建鄰接矩陣對CD算法的結果的影響，并得出閾值只要在較寬松范圍內聚類結果都比較理想，并且該區間與數據集自己身分布有關，最佳閾值在數據分布峰值附近。當選取的閾值大于峰值時，由于較多的有用信息被去除，從而導致許多孤立節點，使得聚類算法無法判斷其分類信息，使得聚類結果質量下降；當選取閾值過小于峰值時，有用信息增多的同時噪聲大量增加，也使得無法正確劃分其分類信息；因此采用合適的閾值能去除一部分噪聲的干擾有助于聚類算法識別有用信息。利用序列相似網絡的CD圖聚類法對蛋白質家族劃分，從本實驗結果與實際的平均吻合程度上分析該方法對蛋白質序列家族劃分有較高的準確率。所以綜合考慮利用CD算法用于序列相似網絡聚類分析在蛋白質家族劃分方面是一種高質量的聚類方法。

[1]Altschul S F，Gish W，Miller W，et al.Basic local alignment search tool[J].J Mol Biol，1990，215（3）：403-410.

[2]Pearson W R.Effective protein sequence comparison[J].Meth Enzymol，1996，266：227-258.

[3]Spirin V，Mirny L A.Protein complexes and functional modules in molecular networks[J].PNAS，2003，100（21）：12123-12128.

[4]Enright A J，Van Dongen S，Ouzounis C A.An efficient algorithm for large-scale detection of protein families[J].Nucleic Acids Research，2002，30（7）：1575-1584.

[5]Mei J，He S，Shi G，et al.Revealing network communities through modularity maximization by a contraction-dilation method[J].New Journal of Physics，2009，11（4）.

[6]Punta M，Coggill P C，Eberhardt R Y，et al.The pfam protein families database[J].Nucleic Acids Research，2011，40（D1）：D290-D301.

[7]Mowat C G，Chapman S K.Multi-heme cytochromes—new structures，new chemistry[J].Dalton Transactions，2005（21）：3381-3389.

[8]Foggia P，Percannella G，Sansone C，et al.A graph-based clustering method and its applications[Springer Berlin/Heidelberg.2007：277-287.

[9]Bello-Orgaz G，Menéndez H D，Camacho D.Adaptive k-means algorithm for overlapped graph clustering[J].Int J Neural Syst，2012，22（5）.

[10]Santini G，Soldano H，Pothier J.Automatic classification of protein structures relying on similarities between alignments[J].BMC Bioinformatics，2012，13（1）.

[11]He J，L C，Y B，et al.Efficient and accurate greedy search methods for mining functional modules in protein interaction networks[J].BMC Bioinformatics，2012，13.

[12]Seah B S，Bhowmick S S，Forbes Dewey C，Jr.Facets：Multi-faceted functional decomposition of protein interaction networks[J].Bioinformatics，2012，28（20）：2624-2631.

[13]Solava R W，Michaels R P，Milenkovic T.Graphlet-based edge clustering reveals pathogen-interacting proteins[J].Bioinformatics，2012，28（18）：i480-i486.

[14]Healey C G，Dennis B M.Interest driven navigation in visualization[J].IEEE Trans Vis Comput Graph，2012，18（10）：1744-1756.

[15]Becker E，Robisson B，Chapple C E，et al.Multifunctional proteins revealed by overlapping clustering in protein interaction network[J].Bioinformatics，2012，28（1）：84-90.

[16]González A J，L L，W C H.Predicting ligand binding residues and functional sites using multipositional correlations with graph theoretic clustering and kernel cca[J].IEEE/ACM Trans Comput Biol Bioinform，2012，9（4）：992-1001.

[17]Qian P，Chung F L，Wang S，et al.Fast graph-based relaxed clustering for large data sets using minimal enclosing ball[J].IEEE transactions on systems，man，and cybernetics.Part B，Cybernetics ：a publication of the IEEE Systems，Man，and Cybernetics Society，2012，42：672-687.

[18]Newman M E J，Girvan M.Finding and evaluating community structure in networks[J].Phys Rev E Stat Nonlin Soft Matter Phys，2004，69（2 Pt 2）.

[19]Girvan M，Newman M E J.Community structure in social and biological networks[J].PNAS，2002，99（12）：7821-7826.

[20]M J，Y X，Z W.Revealing remote protein homology with sequence similarity and a modularity-based approach[J].Theor Biol Forum，2011，104（1）：57-68.