錐形永磁軸承磁力解析模型

田錄林 李 鵬

1.西安理工大學，西安，710048 2.甘肅省電力公司電力科學研究院，蘭州，730050

0 引言

要滿足國家裝備制造業對所亟需的精密機床、飛輪儲能裝置、風力發電機等重大裝備關鍵零部件、高性能軸承的巨大需求，要實現旋轉機械節能、高效高速可靠運轉，必須解決高速轉子的支承問題。機械軸承有接觸、需潤滑，限制了它的最高轉速和使用壽命，已成為傳統驅動高速化的瓶頸。磁懸浮軸承無摩擦，可以解決上述問題。但電磁懸浮軸承耗能、控制復雜［1］，超導磁懸浮軸承需要制冷設備［2－3］，這限制了它們的應用，而永磁軸承具有結構簡單、成本低、無摩擦、無能耗、無污染等特點，具有明顯的競爭優勢。永磁軸承有不同的結構形式，相對于其他形式的永磁軸承，錐形永磁軸承具有同時承受徑向和軸向載荷的優點，國內外一些學者對錐形永磁軸承進行了研究，取得了一些進展。Hamler［4］提出了錐形永磁軸承結構，并采用有限元方法對其進行了仿真研究；Compter［5］根據電流模型得出三角形和梯形永磁體磁路模型，推導出磁化方向不同時的磁路計算方程；Bassani等［6］依據等效電流方法，研究分析了錐形永磁軸承磁化方向對磁力大小的影響。但上述研究尚未涉及錐形永磁軸承磁力解析模型的研究。本文針對上述研究的不足和空隙，基于點磁荷二維磁場和虛功原理［7－8］推導出一對平行矩形截面永磁體的磁力解析模型，并結合錐形永磁軸承的結構特點，建立了具有明確參數關系、便于錐形永磁軸承設計的磁力解析模型。該模型通過分析錐形永磁軸承磁力與相關參量的關系，揭示了錐形永磁軸承的動力學特性及規律。ANSYS仿真表明本文模型正確可行，其誤差能夠滿足工程應用的要求。

1 錐形永磁軸承磁力解析模型

錐形永磁軸承結構剖面如圖1所示［9］，該軸承結構用于承載轉軸軸向和徑向載荷。

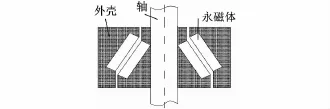
圖1 錐形永磁軸承結構示意圖

為方便建立錐形永磁軸承磁力解析模型，忽略錐形永磁軸承曲率的影響，先研究一對縱向長度為L的兩塊平行矩形截面永磁體磁力解析模型，然后再考慮錐形永磁軸承的結構特點，研究其軸向及徑向分力。

1.1 一對縱向長度為L的兩塊平行矩形截面永磁體磁力解析模型

兩長直細條形永磁體，一塊過P點與Y軸重合，一塊過M點與X軸平行，如圖2所示。基于點磁荷二維磁場和虛功原理，可得單位長度的兩長直細條形永磁體之間的磁力［10］為

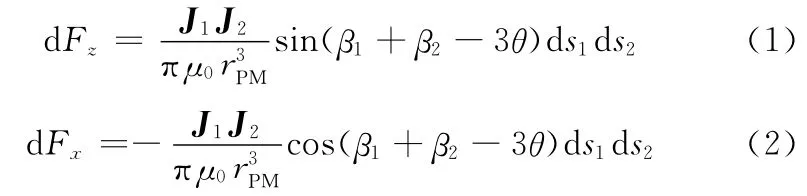
式中，J1、J2分別為永磁體磁極化強度矢量，其在Y 軸方向的分量為0，其量值分別等于永磁體剩磁感應強度Br1和Br2；μ0為空氣磁導率，μ0＝0.4πμH／m；rPM為同一橫截面內兩長條形永磁體兩微元面ds1和ds2間的距離；β1、β2分別為J1和J2與X軸方向的夾角；θ為rPM與X軸正方向的夾角。

圖2 兩長直細條形平行永磁體的參數

縱向長度為L的一對平行矩形截面永磁體如圖3所示，箭頭為磁化矢量方向［11-12］，圖中a為矩形截面長度，b、d分別為內外磁環厚度。

當β1＝π，β2＝π時，則β1＋β2＝2π，對式（1）積分可得

圖3 兩塊平行截面永磁體參數示意圖

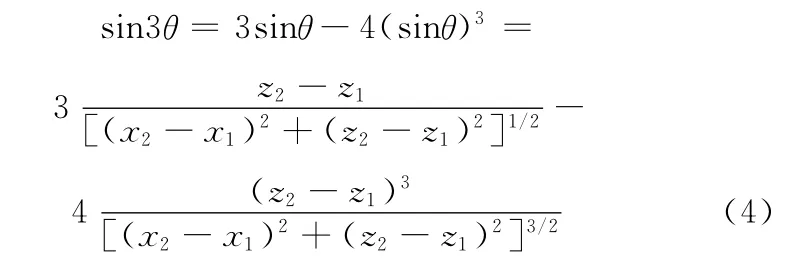
將式（4）代入式（3）化簡積分得

對式（2）積分，可得長度為L的兩塊平行矩形截面永磁體X向磁力：

將式（8）代入式（7）化簡積分可得

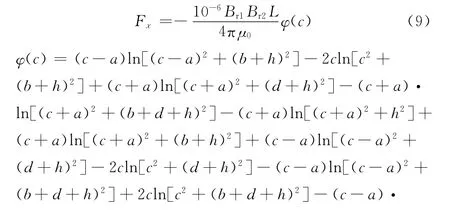
式（5）和式（9）即為一對縱向長度為L的兩塊平行矩形截面永磁體磁力解析模型，式中磁力單位為N，長度單位為mm。

1.2 錐形永磁軸承的軸向磁力和徑向磁力

錐形永磁軸承可視為由兩塊平行矩形截面永磁體以一定傾角環繞轉軸軸線而繞成，可取磁環間隙中間處周長為式（5）和式（9）的縱向近視長度，其軸向及徑向分力是式（5）和式（9）計算磁力在軸向及徑向的分力。

1.2.1軸向磁力

設錐形永磁軸承傾角為α，其剖面參數如圖4所示，點P、Q、R、S分別為錐形軸承剖面末端點，設圖中P點坐標為（w1，v1），Q點坐標為（w2，v2），R 點坐標為（w3，v3），S 點坐標為（w4，v4）。由圖4可得

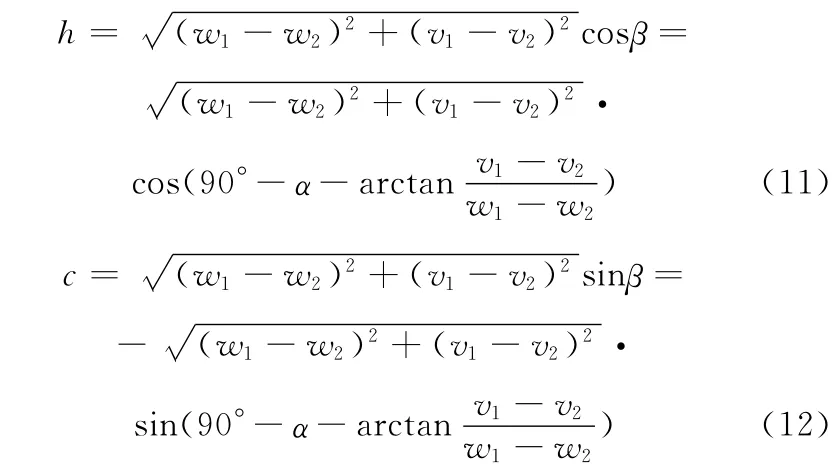
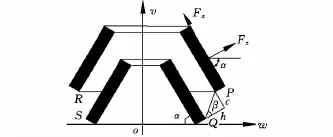
圖4 錐形永磁軸承軸向剖面圖

當錐形永磁軸承承受軸向載荷時，其軸向磁力解析表達式為

1.2.2徑向磁力

圖5為錐形永磁軸承徑向偏移e時的剖面圖，圖中的R1、R2分別表示軸承底部剖面內環外半徑和外環內半徑，且其R1＝｜0.5（w2－w4）｜，R2＝｜0.5（w1－w3）｜。為了利用式（4）、式（5）和式（9）分析圖5徑向偏移e時的錐形永磁軸承徑向磁力，將錐形永磁軸承分為對稱的N（N ＝8）段［13］，其各段徑向偏移間隙可表示為

圖5 錐形永磁軸承徑向剖面參數

設錐形永磁軸承內外磁環厚度相等，即b＝d，錐角為α，單個磁環沿錐角為α方向的長度為a（圖3～圖5），按截面等分原則確定錐形永磁軸承平均磁環周長，設磁環平均周長對應的平均半徑為Rj，則

錐形永磁軸承的近似周長為L＝2πRj。由于磁環間徑向間隙很小，在忽略錐形永磁軸承曲率的情況下，可得圖5中的每段平均弧長Lx為錐形永磁軸承近似周長L的1／N。將hx、Lx代入式（5）和式（9）中，近似計算各段中點對應的徑向磁力和切向磁力，再將以上磁力分別沿徑向（w方向）分解，最后將8段的徑向磁力疊加可得錐形永磁軸承徑向總磁力，即

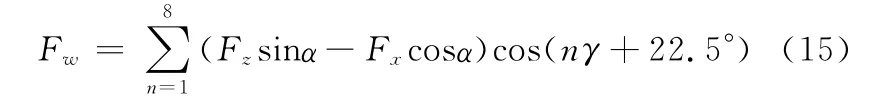
由于圖5以w軸為對稱軸，顯然m方向磁力為零。

2 磁力解析模型的ANSYS仿真驗證及參數分析［14-18］

本文計算分析選用稀土NdFeB作為永磁軸承材 料，其 性 能 參 數 為：Br＝ 1.13T，Hc＝800kA／m，μr＝Br／（μ0Hc）＝1.124。

2.1 解析模型的錐形永磁軸承軸向磁力與軸向偏移的仿真驗證及參數分析

設置的錐形永磁軸承幾何參數為：b＝d＝15mm，a＝30mm，α＝30°，嵌套軸半徑為rg＝21mm，軸承底部4點的坐標分別為：P（54.48mm，12.99mm），Q（54.98mm，13.87mm），R（－54.48mm， 12.99mm），S（－54.98mm，13.87mm）。

錐形永磁軸承僅有軸向偏移時，將相關參數代入式（5）、式（9）～ 式（13）進行計算，計算結果如表1所示，其對應的計算和仿真曲線如圖6所示，圖表中的Fvj為軸承軸向磁力解析模型計算值，Fvf為軸承軸向磁力ANSYS仿真值。計算值與仿真值的最大誤差為4%，最小誤差為0.36%，平均誤差為0.74%。由表1、圖6可以看出，錐形永磁軸承軸向磁力隨軸向偏移的增大而減小。

表1 錐形永磁軸承磁力模型計算值與仿真值

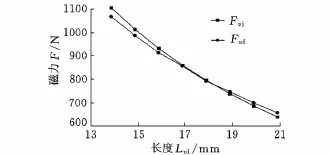
圖6 錐形永磁軸承磁力模型計算曲線與仿真曲線

在ANSYS仿真中，用PLANE53單元建立永磁軸承軸對稱模型。圖7所示為錐形永磁軸承ANSYS仿真二維磁力線。

圖7 ANSYS仿真二維磁力線圖

2.2 錐形永磁軸承軸向磁力與磁環厚度的關系

設置的錐形永磁軸承幾何參數為：a＝30mm，α＝30°，rg＝21mm。將相關參數代入式（5）和式（8）進行計算，然后將計算結果和已知參數代入式（11）～式（13）計算錐形永磁軸承的磁力。錐形永磁軸承軸向磁力解析模型計算結果和ANSYS仿真結果如表2所示，其對應的計算和仿真曲線如圖8所示。計算結果與仿真結果的最大誤差為3.59%，最小誤差為0.16%，平均誤差為1.56%。由表2和圖8可以看出：錐形永磁軸承軸向磁力隨磁環厚度b的增大而增大。

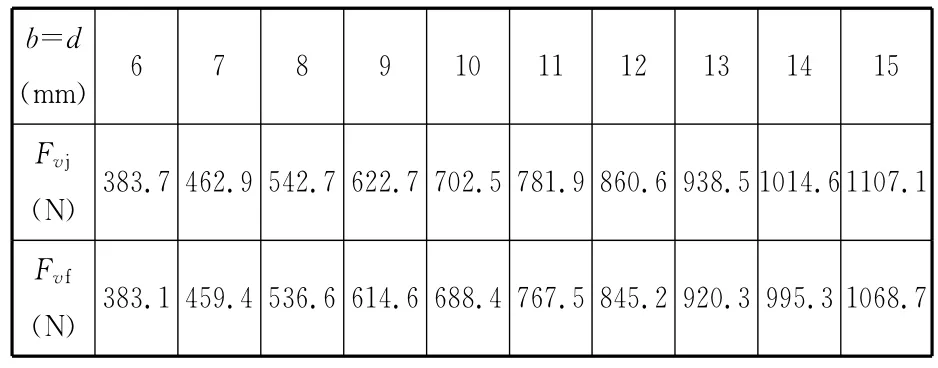
表2 錐形永磁軸承磁力模型計算值與仿真值

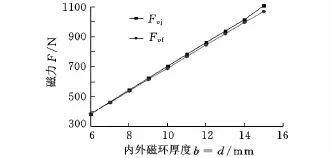
圖8 錐形永磁軸承磁力模型計算曲線與仿真曲線

2.3 錐形永磁軸承軸向磁力與磁環沿錐角為α方向的長度a的關系解析

設置的錐形永磁軸承幾何參數為：b＝d＝15mm，α＝30°。將相關參數代入式（5）和式（9）進行計算，將計算結果和已知參數代入式（11）～式（13）計算錐形永磁軸承磁力。錐形永磁軸承軸向磁力解析模型計算結果和ANSYS仿真結果如表3所示，其對應的計算和仿真曲線如圖9所示。計算結果與仿真結果的最大誤差為0.12%，平均誤差為1.54%。由表3和圖9可以看出：在小范圍內錐形永磁軸承軸向磁力隨單個磁環沿錐角為α方向的長度a的增大而增大。

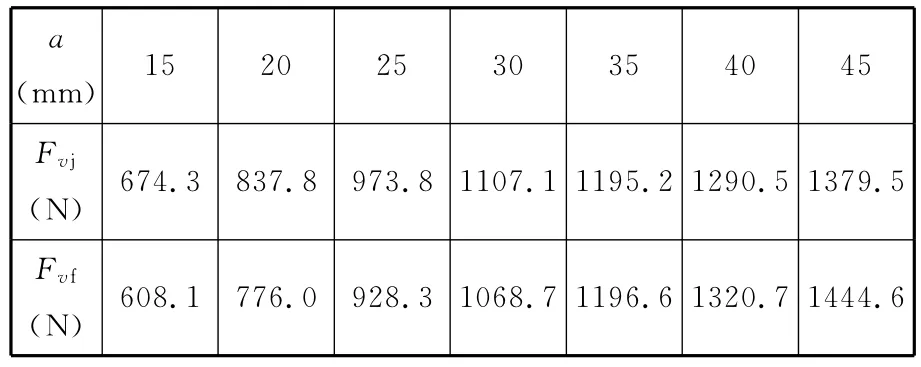
表3 錐形永磁軸承磁力模型計算值與仿真值

2.4 錐形永磁軸承軸向磁力與其錐角α的關系解析

設置的錐形永磁軸承幾何參數為：a＝30mm，b＝d＝15mm。將相關參數代入式（5）和式（9）進行計算，然后將計算所得結果和已知參數代入式（11）～式（13）計算錐形永磁軸承磁力。錐形永磁軸承軸向磁力解析模型計算結果和AN－SYS仿真結果如表4所示，其對應的計算和仿真曲線如圖10所示。計算結果與仿真結果的最大誤差為9.8%，最小誤差為1.94%，平均誤差為3.59%。由表4和圖10可以看出：錐形永磁軸承軸向磁力隨其錐角α的增大而減小。

圖9 錐形永磁軸承磁力模型計算曲線與仿真曲線

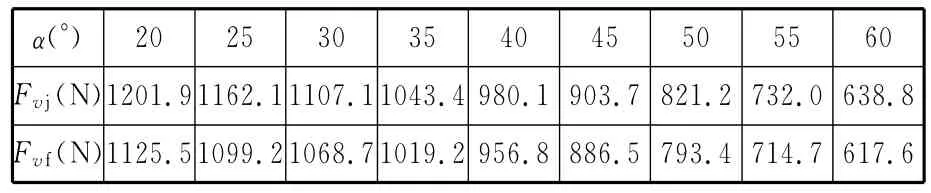
表4 錐形永磁軸承磁力模型計算值與仿真值

圖10 錐形永磁軸承磁力模型計算曲線與仿真曲線

2.5 錐形永磁軸承軸向磁力與嵌套軸半徑γg的關系解析

設置的錐形永磁軸承幾何參數為：a＝30mm，b＝d＝15mm，α＝30°。將相關參數代入式（5）和式（9），然后將計算結果和已知參數代入式（11）～式（13）計算錐形永磁軸承磁力。錐形永磁軸承軸向磁力解析模型計算結果和ANSYS仿真結果如表5所示，其對應的計算和仿真曲線如圖11所示。計算結果和仿真結果的最大誤差為6.79%，最小誤差為0.12%，平均誤差為2.27%。由表5和圖11可以看出：錐形永磁軸承軸向磁力隨嵌套軸半徑rg的增大而增大。

表5 錐形永磁軸承磁力模型計算值與仿真值

2.6 錐形永磁軸承徑向磁力與其徑向偏移量e的關系闡析

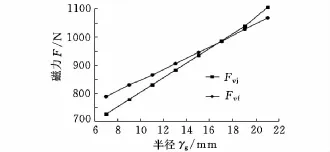
圖11 錐形永磁軸承磁力模型計算曲線與仿真曲線

設置的錐形永磁軸承幾何參數為：a＝30mm，b＝d＝15mm，α＝30°，將相關參數代入式（5）、式（9）、式（12）和式（14）進行計算，然后將計算結果和已知參數代入式（15）計算錐形永磁軸承磁力。錐形永磁軸承徑向磁力解析模型計算結果和ANSYS仿真結果如表6所示，其對應的計算和仿真曲線如圖12所示。計算結果和仿真結果的最大誤差為11.1%，最小誤差為1.7%，平均誤差為2.6%。由表6和圖12可以看出：錐形永磁軸承徑向磁力隨徑向偏移量e的增大而增大。

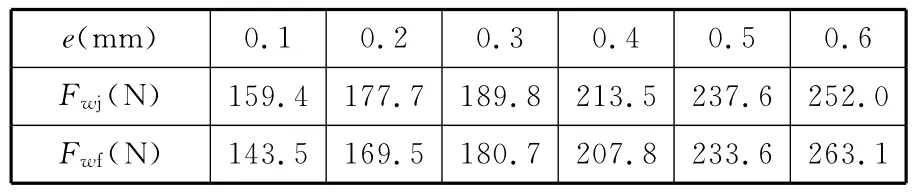
表6 錐形永磁軸承磁力模型計算值與仿真值

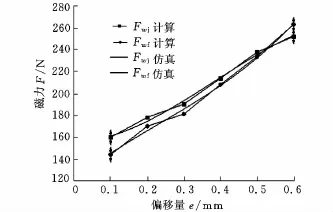
圖12 錐形永磁軸承磁力模型計算曲線與仿真曲線

本文數據誤差產生的主要原因是：計算值中，磁環平均周長對應的平均半徑Rj存在計算誤差；另外，在ANSYS仿真計算中磁體結構建模時也存在誤差。

3 結論

本文建立了錐形永磁軸承磁力解析模型，分析了圓錐形永磁軸承軸向承載力與其結構參數之間的關系。結果表明：圓錐形永磁軸承磁力與磁環的平均周長和磁環磁通密度的平方成正比，磁力隨著磁環徑向寬度的增大而增大，隨磁環截面長度的增大而增大；軸向磁力隨磁環錐角的增大而減小，隨軸向偏移的增大而減小；徑向磁力隨著徑向間隙的增大而增大。解析模型計算結果與ANSYS仿真結果基本一致，最大誤差小于11.1%。本文解析模型計算方法的成功應用，解決了長期以來錐形永磁軸承磁力計算只有復雜的數值仿真算法，而沒有便于工程設計計算的磁力解析模型問題。

［1］田擁勝，孫巖樺，虞烈.高速永磁電機電磁軸承轉子系統的動力學及實驗研究［J］.中國電機工程學報，2012，32（9）：116－123.Tian Yongshen，Sun Yanhua，Yu Lie.Dynamical and Experimental Researches of Active Magnetic Bearing Rotor Systems for High－speed PM Machines［J］.Proceedings of the CSEE，2012，32（9）：116－123.

［2］Ikeda M，Wongsatanawarid A，Seki H，et al.Interaction of Bulk Superconductors with Flywheel Rings Made of Multiple Permanent Magnets［J］.Physica C，2009，469：1270－1273.

［3］Deng Z，Lin Q，Wang J，et al.Basic Design and Characteristics Study of a Double－axial Superconducting Magnetic Bearing System［J］.Cryogenics，2009，49：259－262.

［4］Hamler A.Passive Magnetic Bearing［J］.Journal of Magnetism and Magnetic Materials，2004（272／276）：2379－2380.

［5］Compter J C.Ampere’s Circuital 3－D Model for Noncuboidal Magnets［J］.IEEE Transactions on Magnetics，2010，46（12）：4009－4015.

［6］Bassani R，Ciulli E，di Puccio F，et al.Study of Conic Permanent Magnet Bearings［J］.Meccanica，2001，36：745－754.

［7］馮慈章.電磁場［M］.北京：高等教育出版社，2004.

［8］王秀和.永磁電機［M］.北京：中國電力出版社，2007.

［9］胡業發，許開國，張錦光，等.磁懸浮風力發電機用磁力軸承的分析與設計［J］.軸承，2008（9）：6－10.Hu Yefa，Xu Kaiguo，Zhang Jinguang，et al.Analysis and Design of Magnetic Bearings Used in Magnetic Suspending Wind Power Generator［J］.Bearing，2008（9）：6－10.

［10］田錄林，李言，安源，等.軸向放置軸向磁化的雙環永磁軸承徑向磁力研究［J］.中國機械工程，2007，18（24）：2926－2929.Tian Lulin，Li Yan，An Yuan，et al.Research on the Radial Magnetic Force of Axial Placement and Axial Magnetization Bi－annular－shaped PMB［J］.China Mechanical Engineering，2007，18（24）：2926－2929.

［11］田錄林，張靠社，楊曉萍，等.永磁導軌懸浮和導向磁力研究［J］.中國電機工程學報，2008，28（21）：135－139.Tian Lulin，Zhang Kaoshe，Yang Xiaopin，et al.Research on the Axial Magnetic Force of Axially Magnetized Bi－annular－shaped Permanent Magnetic Bearings［J］.Proceedings of the CSEE，2008，28（21）：135－139.

［12］田錄林，賈嶸，楊國清，等.永磁鐵切合體的磁場及磁力［J］.電工技術學報，2008，23（6）：7－13.Tian Lulin，Jia Rong，Yang Guoqing，et al.Research on the Magnetic Field and Magnetic Force of a Permanent Magnet Affixed to a Plane Magnetizer［J］.Transactions of China Electrotechnical Society，2008，23（6）：7－13.

［13］田錄林，李言，田琦，等.軸向放置的軸向磁化多環永磁軸承徑向磁力研究［J］.中國機械工程，2008，19（10）：1163－1166.Tian Lullin，Li Yan，Tian Qi，et al.Research on the Radial Magnetic Force of Axial Placement and Axial Magnetization Multiannual－shaped Permanent Magnetic Bearings［J］.China Mechanical Engineering，2008，19（10）：1163－1166.

［14］唐輝.被動磁懸浮軸承及電渦流傳感器的研究［D］.西安：西安交通大學，2003.

［15］崔鵬，張錕，李杰.基于許－克變換的懸浮電磁鐵力與轉矩解析計算［J］.中國電機工程學報，2010，30（24）：129－134.Cui Peng，Zhang Kun，Li Jie.Calculation of Electromagnetic Force and Torque of Suspension Electromagnet Based on Schwarz－christoffel Transform［J］.Proceedings of the CSEE，2010，30（24）：129－134.

［16］Bassani R.Dynamic Stability of Passive Magnetic Bearings［J］.Nonlinear Dyn，2007，50：161－168.

［17］李麗君，房建成，韓邦成，等.磁懸浮風力發電機用錐形被動磁軸承分析與設計［J］.軸承，2010（1）：10－14.Li Lijun，Fang Jiancheng，Han Bangcheng，et al.Analysis and Design of Conic Passive Magnetic Bearing for Magnetic Suspension Wind Turbine［J］.Bearing，2010（1）：10－14.

［18］Azukizawa T，Yamamoto S，Matsuo N.Feasibility Study of a Passive Magnetic Bearing Using the Ring Shaped Permanent Magnets［J］.IEEE Transactions on Magnetics，2008，44（11）：4277－4280.