柔性轉子滾動軸承系統混沌行為研究

崔 立 鄭建榮

1.上海第二工業大學，上海，201209 2.華東理工大學，上海，200237

0 引言

滾動軸承支承的轉子系統由于軸承非線性剛度而出現復雜的非線性動力學特性。近年來，剛性轉子滾動軸承系統的分叉及混沌特性研究得到了廣泛的重視。

Jang等［1］考慮滾動軸承的5個自由度以及表面波紋度建立了剛性轉子滾動軸承系統的非線性動力學方程，發現套圈的波紋會導致徑向位移和角位移響應峰值附近出現邊頻帶。Harsha［2－3］考慮軸承間隙、不平衡力研究了轉子系統的動力學響應，發現系統的動力學行為與滾動體的通過頻率有關，且當通過頻率及其諧波與固有頻率相等、外圈波紋度階數與滾動體數目相等時振動幅值將變得極大。Bai等［4］研究了主軸－滾動軸承系統非線性動力學行為，發現軸承間隙的減小有利于提高主軸軸承系統的穩定性。高尚晗等［5］研究了主軸－滾動軸承在負游隙情況下的機床主軸－滾動軸承系統的非線性動力學特性，揭示了主軸系統的混沌演化過程。崔立等［6］研究了圓柱滾子軸承剛性轉子系統周期運動分岔特性，發現隨著徑向間隙、阻尼和力矩的變化，周期運動將產生倍周期或Hopf分岔，分岔轉速隨參數變化而改變。

以上的研究對象均為剛性轉子，模型涉及轉軸的彎曲變形和陀螺力矩等參數。隨著旋轉機械轉速的提高，柔性轉子系統的設計與分析變得越來越重要。近年也有一些研究柔性轉子軸承系統的文章發表，如：Laha等［7］研究了油膜軸承支承的柔性轉子系統的分叉行為，分析了轉軸的材料、剛度和質量等參數對轉子系統分叉行為的影響。Villa等［8］、Sinou［9］研究了球軸承支承的柔性轉子系統的非線性動力學行為，發現系統響應中存在跳躍現象和超諧波，但其研究僅考慮了4個自由度的轉軸節點和2個軸承自由度，難以滿足實際工況的需求。

本文采用12自由度Euler－Bernoulli桿單元建立柔性轉子滾子軸承系統的非線性動力學模型，研究系統的混沌行為，分析軸承結構參數與轉軸結構參數對轉子系統混沌行為的影響規律。

1 計算模型

圖1所示為柔性轉子軸承系統模型，采用12自由度的Euler－Bernoulli桿單元，圓盤簡化為質點并考慮其質量與轉動慣量，轉子由兩個滾動軸承支承。

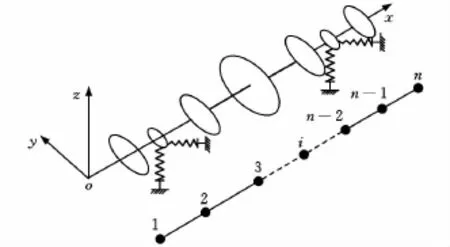
圖1 柔性轉子滾動軸承系統模型

1.1 柔性轉子軸承系統動力學模型

柔性轉子系統的動力學方程為

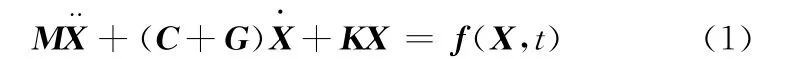
式中，M為包含轉軸、圓盤和軸承的總質量矩陣；C為總阻尼矩陣；G為總陀螺矩陣；K為總剛度矩陣；X為轉子各節點的位移向量；f（X，t）為包括轉子各節點軸承力、重力、轉子不平衡力和外載荷的矩陣。

先對轉子系統進行軸段與節點劃分，然后進行轉子系統的質量矩陣、剛度矩陣、阻尼矩陣、陀螺矩陣、載荷矩陣求解，并按照節點的順序對各矩陣進行組裝，具體過程如下：首先計算桿單元的質量矩陣、陀螺矩陣、剛度矩陣、載荷矩陣并組裝；然后將剛性圓盤的質量矩陣、陀螺矩陣、不平衡力矩陣疊加到所在節點的相應矩陣中；之后將支承軸承的質量矩陣、非線性軸承力疊加到所在節點的相應矩陣中；最后計算系統的結構阻尼、軸承阻尼矩陣并組裝。

1.2 桿單元

圖2所示為針對空間桿單元分析獲得的空間桿單元兩端節點位移。

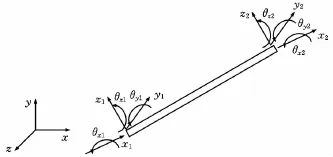
圖2 二節點空間桿單元

針對圖2中12自由度Euler－Bernoulli桿單元，若每個節點考慮6個自由度，則共有6個廣義位移和6個廣義力，其表達式為

式中，xi、yi、zi分別為節點i沿x、y、z方向的線位移；θxi、θyi、θzi分別為節點i處截面繞x、y、z軸的轉角位移；Fxi、Fyi、Fzi分別為節點i在x、y、z方向受到的軸向力和剪切力；Mxi、Myi、Mzi分別為節點i在x、y、z方向所受的扭矩和彎矩。

假設已知桿單元橫截面面積、截面慣性矩、單元的扭轉慣性矩、長度、材料彈性模量和剪切模量，則可根據有限元理論［10］求出桿單元的質量矩陣Ms、剛度矩陣Ks、阻尼矩陣Cs、陀螺矩陣Gs。

1.3 剛性圓盤模型

當軸上安裝有圓盤時，將其視為剛性圓盤，并將其質量矩陣、陀螺矩陣、不平衡力矩陣疊加到所在節點的相應矩陣中。

假設已知圓盤的質量、半徑、不平衡質徑積，則可建立剛性圓盤的質量矩陣Md、陀螺矩陣Gd、不平衡力矩陣Fd，其中Fd為

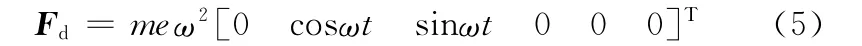
式中，me為圓盤的不平衡質徑積；ω為轉速。

1.4 滾子軸承模型

考慮普遍受載的圓柱滾子軸承，其模型如圖3所示，圖中，Dr為滾子直徑，D1、D2分別為外圈外徑和內圈內徑，δ0為徑向間隙，le為帶凸度滾子的長度，ls為帶凸度滾子直線部分的長度。

假設滾子數目為N，使用切片法將滾子分成nr個圓片。對第j個滾子進行受力分析，假設第j個滾子方位角為φj，根據赫茲接觸理論，并使用擬動力學方法建立滾子軸承的非線性平衡方程組，使用Newton－Raphson法可求出滾子與套圈的接觸力［11］。將各滾子的接觸力分解，即可求出圓柱滾子軸承的非線性軸承力矩陣：

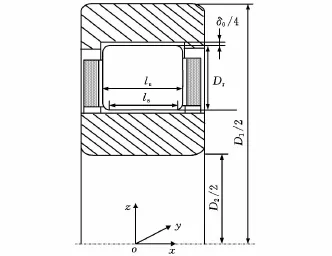
圖3 圓柱滾子軸承結構簡圖

式中，F2jk為第j個滾子的第k個切片與滾子軸承內圈的作用力。

1.5 結構阻尼求解

Rayleigh提出的結構阻尼模型計算表達式為

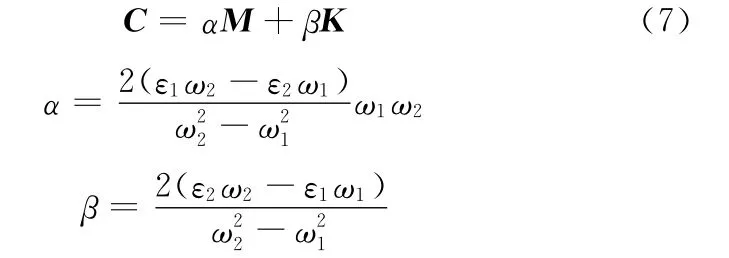
式中，ε1、ε2為兩個振型的阻尼比，根據經驗取ε1＝0.005，ε2＝0.01；ω1、ω2為轉子系統的二階固有頻率。

式（7）中轉子系統的固有頻率ω1、ω2可根據計算得到的質量矩陣、剛度矩陣解｜K－Mω2｜＝0得到。

2 計算方法

采用Runge－Kutta法、Newton－Raphson法進行非線性動力學方程組求解，根據FPA修正法確定求解周期，然后求解最大Lyapunov指數，判斷系統的動力學行為。

2.1 求解周期的確定

轉子軸承系統中存在軸承變剛度激勵，還可能存在不平衡力激勵。不平衡力產生的激勵周期為軸轉動周期的整數倍，但軸承的變剛度激勵周期往往不是軸轉動周期的整數倍，所以在判斷和求解時，采用修正的FPA法建立統一的求解周期［12］，其表達式定義為

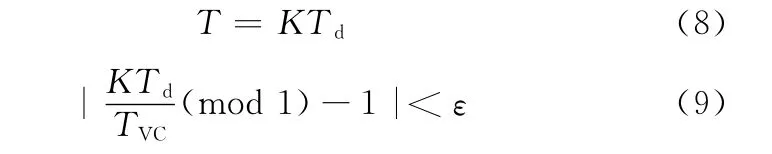
式中，T為求解周期；Td為不平衡力激勵周期；TVC為軸承變剛度激勵周期；ε為常數，取ε＝0.01；K為比例系數，K ＝1，2，…，nk。

根據式（9）進行循環計算，直至找到滿足其要求的K值，代入式（8）即得求解周期。

2.2 Lyapunov指數計算

Lyapunov指數表示在相平面中2條相鄰軌線間的距離隨時間的平均指數發散率，它明確地區分了確定性運動和混沌運動［13］。

對于連續系統有

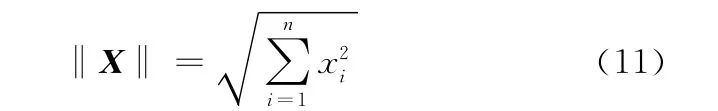
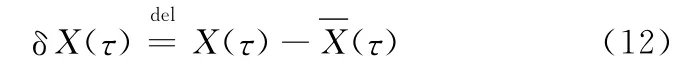
設在τ0時刻‖δX（τ0）‖充分小，于是1維的Lyapunov指數可定義為

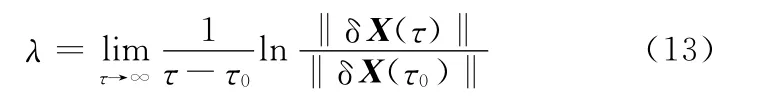
在n維連續系統中，δX（τ）在每個基底上有分量，每一個分量均可按上式求出一個λ，因此共存在n個Lyapunov指數λi，稱為Lyapunov指數譜。當任意選取矩陣δX（τ）時，Lyapunov指數以概率1可能取得最大值，如果其中最大的Lyapunov指數λmax＞0，則該系統一定存在混沌運動。因此，只要計算出系統的最大Lyapunov指數，就可以判斷系統是否處于混沌狀態。

3 計算與分析

圖4為柔性轉子系統簡圖，轉軸由兩個型號相同的滾子軸承支承，轉軸中有剛性圓盤，該圓盤可施加不平衡力。

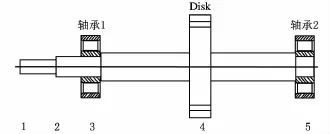
圖4 柔性轉子系統簡圖

表1所示為滾子軸承的結構參數，其中，軸承的彈性模量為204GPa，泊松比為0.3，阻尼為200N·s／m，軸承載荷為｛0，2000N，2000N，0，0｝。

表1 滾子軸承的結構參數

柔性轉子系統的結構參數如表2所示，轉軸被劃分為4個軸段，轉子系統劃分為5個節點。轉軸的彈性模量為204GPa，泊松比為0.3。

表2 柔性轉子系統結構參數

對圖4所示的柔性轉子系統進行計算，判斷圓盤節點處的混沌行為，并分析軸承徑向間隙、圓盤不平衡力、轉軸剛度比等參數對系統混沌行為的影響規律。

3.1 徑向間隙影響分析

假設系統不平衡力為0，則軸承徑向間隙對系統混沌特性的影響如圖5所示。分別取40μm、60μm和80μm的徑向間隙計算系統的最大Lyapunov指數。

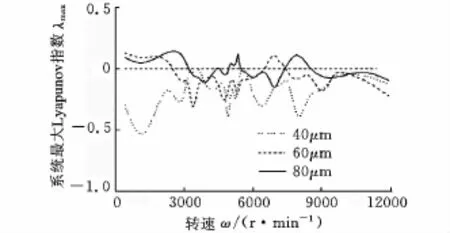
圖5 不同節點處的最大Lyapunov指數

系統最大Lyapunov指數小于0，表明系統運動是穩定的；當最大Lyapunov指數等于0時，系統為倍周期或擬周期分叉運動；當最大Lyapunov指數大于0時，系統為混沌運動。

為了驗證計算的準確性，使用Runge－Kutta法進行非線性動力學方程組求解，得到轉子系統響應的頻譜圖和Poincaré截面。從圖5可知，當徑向間隙為80μm、轉速為4200r／min時，系統的最大Lyapunov指數等于0（圖中fVC為滾子軸承的變剛度振動頻率）。圖6所示為圖5工況下圓盤節點處的頻譜圖和Poincaré截面，圖形表明系統為擬周期振動。

圖6 轉速為4200r／min、徑向間隙為80μm時的響應

圖5表明，徑向間隙為80μm、轉速為8000 r／min時，系統的最大Lyapunov指數大于0，圖7所示為對應該工況的圓盤節點處的頻譜圖和Poincaré截面，其表明系統為混沌運動。

圖5還表明，當徑向間隙為40μm時，系統的最大Lyapunov指數小于0，未出現混沌行為；當徑向間隙為60μm 時，在0～2500r／min、6600～7200r／min轉速下的最大Lyapunov指數大于0，系統出現混沌行為；當徑向間隙為80μm時，在0～3100r／min、5000～5400r／min、7500～8500 r／min轉速下出現混沌行為。

3.2 不平衡力影響分析

圖8所示為在其他條件不變前提下的不平衡力對系統混沌特性的影響。分別取圓盤的不平衡質徑積為5×10－6kg·m、1×10－5kg·m、2×10－5kg·m，計算系統的最大Lyapunov指數。

從圖8可知，當不平衡質徑積為5×10－6kg·m時，在0～2000r／min，系統出現混沌行為；當不平衡質徑積為1×10－5kg·m時，在0～3700r／min，系統出現混沌行為；當不平衡質徑積為2×10－5kg·m時，在0～4400r／min，系統出現混沌行為。可以看出，不平衡力的存在會改變系統的混沌行為，系統出現混沌的轉速及范圍隨著不平衡力的增大逐漸增大。

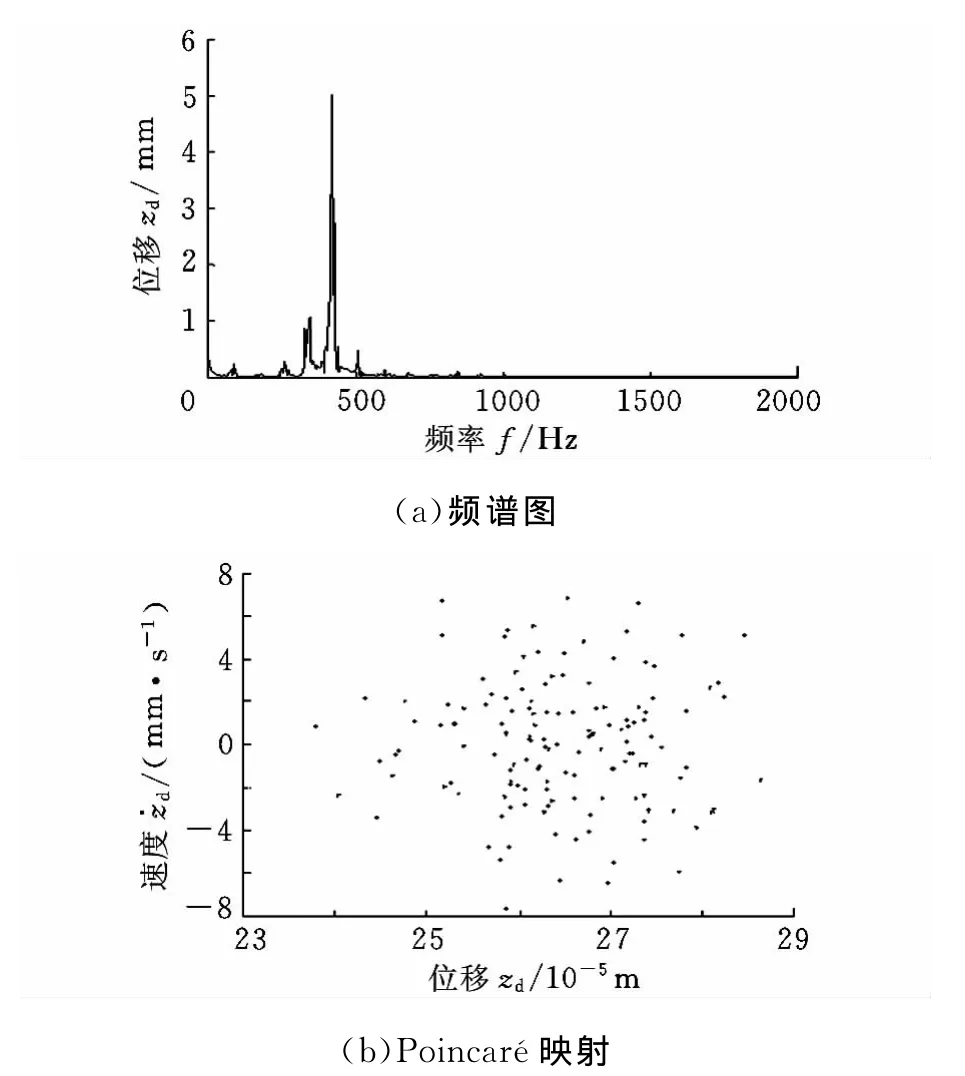
圖7 轉速為8000r／min、徑向間隙為80μm時的響應

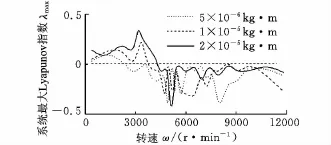
圖8 不同不平衡力時的系統最大Lyapunov指數

3.3 剛度比影響分析

定義柔性轉子系統的剛度比為

式中，Kshaft為柔性轉軸的剛度；Kbearing為支承軸承剛度。

在其他參數不變的情況下，分別取長度為500mm、400mm、300mm的轉軸進行剛度比計算，其對應所得的剛度比分別為7.38×10－3、1.43×10－2、3.31×10－2，據此，可得出剛度對于柔性轉子系統動力學特性的影響。

圖9所示為不同剛度比時圓盤節點處的振幅隨轉速變化曲線，可以看出，隨著剛度比的增大，振幅峰值對應的轉速逐漸增大，即臨界轉速增大；振幅峰值也隨著剛度比增大而增大，且臨界轉速附近的峰值逐漸變多，可以看出隨著轉軸剛度增大，軸承非線性振動對轉子系統的影響增大，導致系統響應復雜。

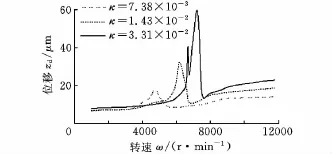
圖9 不同剛度比時的圓盤節點振幅

圖10所示為不同剛度比時最大Lyapunov指數隨轉速的變化曲線。當剛度比為7.38×10－3時，在0～800r／min出現混沌行為。當剛度比為1.43×10－2時，在0～1200r／min、5200～5400r／min出現混沌行為。當剛度比為3.31×10－2時，在0～3200r／min、4800～5900r／min出現混沌行為。

圖10 不同轉軸剛度比時的系統最大Lyapunov指數

可見，隨著轉軸剛度增大即剛度比增大，混沌運動的區間發生改變。隨著剛度比的增大，系統的混沌區間增大，軸承引起的轉子系統非線性行為明顯。對比柔性轉子和剛性轉子的混沌特性，發現軸承的非線性接觸力對剛性轉子系統的混沌特性影響大于柔性轉子。

4 實驗

為驗證本文方法對柔性轉子系統動力學行為預測的準確性，使用圖11所示的高速滾子軸承柔性轉子實驗器進行測試。動力裝置的高速電主軸，最高轉速可達24 000r／min，實驗滾子軸承參數如表1所示，實驗過程中滾子軸承承受的徑向載荷為2000N。采用非接觸式的電渦流傳感器測量滾子軸承及圓盤處的徑向振動位移。

圖12所示為轉子圓盤處振動位移幅值計算結果與實驗結果對比，可以看出，計算得到的一階臨界轉速為4900r／min，實驗得到的一階臨界轉速為4700r／min，與計算結果較為接近；實驗測試振幅與計算結果也較為接近，證明了本文方法的準確性。

圖11 滾動軸承轉子系統實驗器

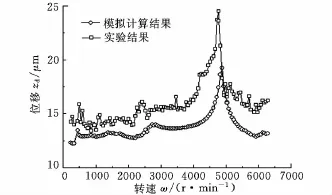
圖12 幅值計算結果與實驗結果對比

5 結論

（1）軸承徑向間隙是影響轉子系統非線性振動特性的重要參數。隨著軸承徑向間隙的增大，系統的混沌區間逐漸增大、變多。

（2）不平衡力的存在對系統混沌行為也有較大的影響。系統出現混沌的轉速及范圍隨著不平衡力的增大逐漸增大。

（3）隨著轉軸剛度比增大，轉子振幅峰值以及對應的轉速均逐漸增大。共振轉速附近產生混沌運動對應的轉速增大時，系統混沌區間也增多，軸承非線性對系統響應影響明顯。

［1］Jang G H，Jeong S W.Nonlinear Excitation Model of Ball Bearing Waviness in a Rigid Rotor Supported by Two or More Ball Bearings Considering Five Degrees of Freedom［J］.Transactions of the ASME，2002，124：82－90.

［2］Harsha S P.Non－linear Dynamic Analysis of an Unbalanced Rotor Supported by Roller Bearing［J］.Chaos，Solitons and Fractals，2005，26：47－66.

［3］Harsha S P.Non－linear Dynamic Response of a Balanced Rotor Supported by Rolling Element Bearings Due to Radial Internal Clearance Effect［J］.Mechanism and Machine Theory，2006，41：688－706.

［4］Bai Changqing，Xu Qingyu.Dynamic Model of Ball Bearings with Internal Clearance and Waviness［J］.Journal of Sound and Vibration，2006，294：23－48.

［5］高尚晗，龍新華，孟光.主軸－滾動軸承系統三種分岔形式［J］.振動與沖擊，2009，28（4）：59－64.Gao Shanghan，Long Xinhua，Meng Guang.Three Bifurcation Types in the Spindle－ball Bearing System［J］.Journal of Vibration and Shock，2009，28（4）：59－64.

［6］崔立，劉長利，鄭建榮.圓柱滾子軸承剛性轉子系統周期運動分岔研究［J］.振動、測試與診斷，2011，31（5）：637－641.Cui Li，Liu Changli，Zheng Jianrong.Periodic Motion Bifurcation of Rigid Rotor System in Cylinder Roller Bearing［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31（5）：637－641.

［7］Laha S K，Kakoty S K.Non－linear Dynamic Analysis of a Flexible Rotor Supported on Porous Oil Journal Bearings［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16：1617－1631.

［8］Villa C，Sinou J J，Thouverez F.Stability and Vibration Analysis of a Complex Flexible Rotor Bearing System［J］.Communications in Non－linear Science and Numerical Simulation，2008，13：804－821.

［9］Sinou J J.Non－linear Dynamics and Contacts of an Unbalanced Flexible Rotor Supported on Ball Bearings［J］.Mechanism and Machine Theory，2009，44：1713－1732.

［10］Wang Maocheng.Finite Element Method［M］.Beijing：Tsinghua University Press，2008.

［11］Harris T A.Rolling Bearing Analysis［M］.New York，USA：John Wiley ＆Sons，2001.

［12］Choi S K，Noah S T.Response and Stability Analysis of Piecewise Linear Oscillations under Multi－forcing Frequencies［J］.Nonlinear Dynamics，1992，3：105－121

［13］Wolf A，Swift J B，Swinney H L.Determining Lyapunov Exponents from a Time Series［J］.Physica D.，1985，16：285－317.