基于相對距離尺度TOPSIS法的機床結構優選設計研究

陳永亮 韓 瑤 龐錦平 劉 譜 潘高星

1.天津大學，天津，300072 2.天津第二機床有限公司，天津，300409

0 引言

機床的大件結構是數控機床的重要部件，其結構性能極大程度地影響加工精度。機床的大件結構的拓撲結構、筋板厚度、高度、出砂孔尺寸等又直接影響大件結構的動靜熱態特性。通過有限元分析方法得到方案各個性能評價指標值，在結構方案的確定過程中，往往采用綜合評價的方法對多種方案進行評價，因此評價方法的選擇至關重要。文獻［1］基于結構配置與性能改進的綜合定量評價方法，得出某大型內齒輪銑齒機的床身最優改進方案；文獻［2］根據可適應原則建立結構性能指標的綜合評價函數，并通過內齒輪銑齒機床立柱元結構的參數優化驗證了其有效性。文獻［3］通過對床身進行APDL參數化建模和模態分析，經簡單的數據比較得出最優參數方案。文獻［4］通過橫梁結構優化有效減小了主要熱源的生熱速率和熱傳導系數。文獻［5］以層次分析法確定對象各屬性權重，然后用基于歐幾里德距離（簡稱歐氏距離）的TOPSIS方法對各商家競爭力進行排序，根據各方案相對理想解的接近程度初步評估選擇較佳方案。文獻［6］采用灰關聯分析和基于歐氏距離的TOPSIS方法進行各游戲廠商的經營績效評估，并通過三種方法的評價對比，總結其各自方法的優缺點。文獻［7］通過采用目標規劃的優化模型和高等數學的方法計算各評價指標的權重，弱化了傳統TOPSIS方法確定權重的主觀程度。文獻［8］利用灰色系統理論，整合不同的評價理論，提出了灰關聯評價方法，并將該方法應用于具體事例，從基于不同基礎功能和可適應功能的設計方案中優選出最佳方案。

本文根據可適應設計原則，通過有限元分析得到各個方案的評價指標值，采用不同距離尺度的TOPSIS方法對機床橫梁結構進行優選，并對不同距離尺度評價結果進行比較和分析。

1 機床結構的可適應設計

機床結構修改的一般過程如圖1所示。首先根據功能要求創新或者根據經驗進行初步總體方案設計；然后在此基礎上進行功能分解，將機床結構劃分為子模塊，再通過參數驅動獲得各個設計方案，對各個方案進行有限元分析，從而對產品性能進行綜合評價對比以確定最優方案。

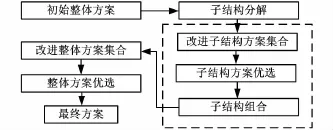
圖1 機床結構可適應設計過程

對于機床橫梁結構，評價其性能的指標有質量、固有頻率、靜剛度和熱特性等多項。因此，建立一個能全面反映機床性能的評價模型，通過對機床結構的不同性能方案進行綜合度量來評價各個方案的性能優劣尤其重要。

2 評價指標和權重的確定

假設S＝｛S0，S1，…，Sm｝是橫梁結構的m種變型，對每個評價目標進行質量測量、動態分析、靜力分析及熱分析，得出其質量m、三向靜力變形（dx，dy，dz）、三向熱變形（δx，δy，δz），以及約束模態的前三階固有頻率（f1，f2，f3）和自由模態的前三階固有頻率（f′1，f′2，f′3）等n個評價指標，進而可得綜合評價因素集中的5個一級指標，其表達式為

式中，X1為質量指標；X2為靜變形指標；X3為熱變形指標；X4為約束模態固有頻率指標；X5為自由模態固有頻率指標。

每個一級指標所包含的若干個二級指標可表示為

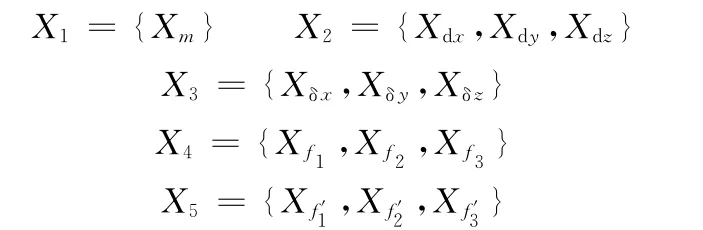
于是，總因素指標集共有n＝13個評價指標，規定J1＝ ｛X1，X2，X3｝為 成 本 型 指 標 集，J1＝｛X4，X5｝為收益型指標集。收益型指標越大，對評估結果越有利；成本型指標越小，對評估結果越有利。反之，則對評估結果不利。

對于本文采取的評價方法，首先確定各指標的權重系數。一級評價指標對應的各指標權重系數可表示為

二級評價指標對應的各指標權重系數可表示為

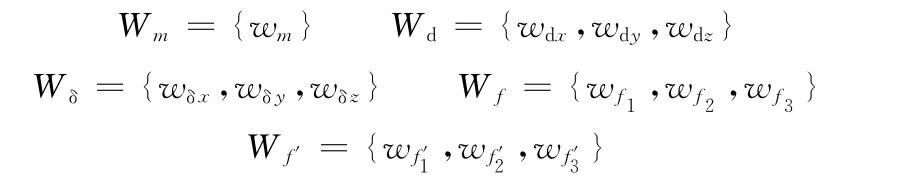
將權重系數W 合成可得

且∑W ＝1。

3 TOPSIS評價方法的數學模型

逼近理想解的排序方法（technique for order preference by similarity to ideal solution，TOPSIS）是 Hwang等［9］于1981年首次提出的，它借助多屬性問題的理想解和負理想解給方案集中各方案排序。

3.1 計算規范化矩陣

首先，根據每個評價目標的n個定量指標值建立特征矩陣：

然后，根據特征矩陣計算規范化矩陣，得到規范化表達式：

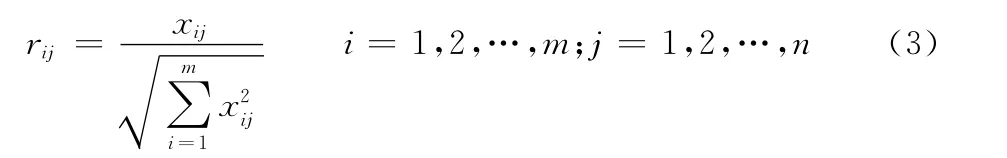
3.2 構造評價指標權重規范化矩陣

通過計算評價指標權重規格化值vij，建立的評價指標權重規范化矩陣為

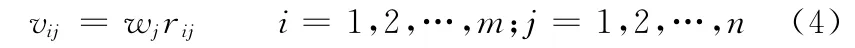
式中，vij為第j個目標的第i個評價指標的權重規格化值。

3.3 確定理想解和反理想解

根據權重規格化值vij所確定的理想解A＊和反理想解A－的表達式為

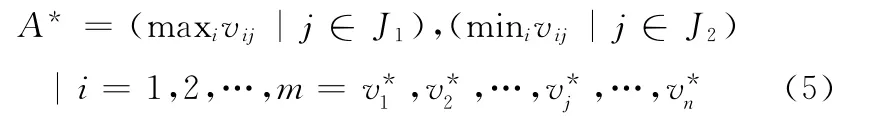
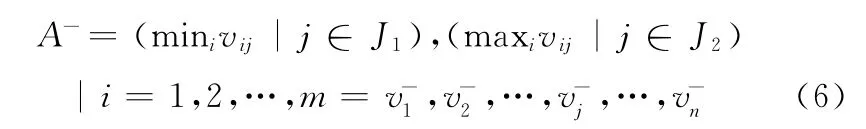
3.4 計算距離尺度

計算距離尺度即計算每個目標到理想解和反理想解的距離，目標到理想解A＊的距離為S＊，到反理想解A—的距離為S—。

S＊為各評價目標與最優目標的接近程度，S＊值越小，評價目標距離理想目標越近，方案越優。

3.5 計算理想解的貼近度

理想解的貼近度表達式為

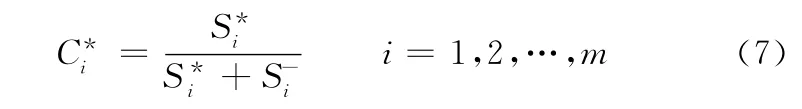
根據C＊值的大小可判斷評價目標的優劣，該值越大，表明評價方案越優。

4 距離尺度的計算

用理想解求解多屬性決策問題的概念簡單，只要在屬性空間定義適當的距離測度就能計算備選方案的理想解。在TOPSIS方法中，距離尺度的計算通常采用明考斯基距離，常用的歐式距離是明考斯基距離的特殊情況。由于明考斯基距離是一種絕對距離，研究表明，它會因固有頻率、變形等評價指標的單位不同而難以明顯區分不同方案的優劣，因此，本文引入了蘭氏距離、基于相似性的差異性距離等相對距離法，以減小數據測量對單位的敏感性。

4.1 歐氏距離

歐氏距離尺度通過n維歐幾里德距離尺度進行計算，其目標到理想解A＊的距離為S＊，到反理想解A—的距離為S，其表達式為

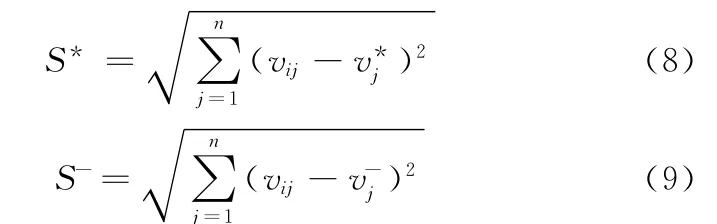
式中，v＊j與分別為第j個目標到最優目標及最劣目標的距離。

4.2 蘭氏距離

蘭氏距離［10］是定義在歐氏空間上的一種度量，蘭氏距離與各變量的單位無關。由于蘭氏距離對大的異常值不敏感，故適用于高度偏斜的數據。根據蘭氏距離的定義［11］，目標到理想解A＊的蘭氏距離為，到反理想解A—的蘭氏距離為，其表達式為

4.3 相似距離

20世紀90年代，周美立［12］提出了用于計算系統相似度的新理論，其理論針對明考斯基距離尺度域值［0，∞］的局限性，采用以相似性為基礎的差異性度量［13-14］計算目標到理想解A＊的差異性距離和到反理想解的差異性距離。其表達式為

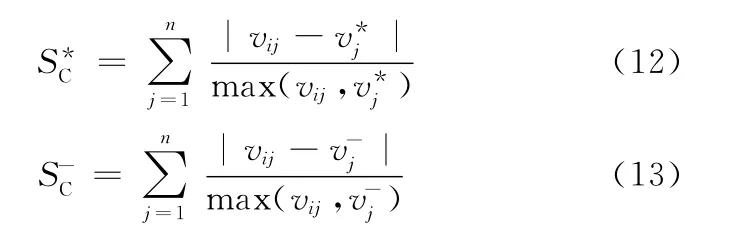
5 立式磨床橫梁結構優選

5.1 立式磨床橫梁結構動靜熱態特性有限元分析

三種立式磨床橫梁基礎結構方案如圖2所示。圖2a為橫梁立柱分離式結構，其固定約束加于底部地腳螺釘處及與床身相連接處；圖2b為橫梁一體式結構，其固定約束加于底部地腳螺釘處；圖2c為在圖2b基礎上將導軌以下部分截掉而成的結構，其底部約束加于底部地腳螺釘處。

圖2 橫梁初始結構選型

橫梁的改進思路為：①拓撲結構改進提高靜剛度；②減小重量；③提高固有頻率；④減少熱變形。改進方案如表1所示。對三種橫梁結構進行動靜及熱態分析；采用ANSYSWorkbench軟件對12種橫梁結構進行自動網格劃分，建立有限元模型；然后定義材料屬性，材料特性數據如表2所示。

表1 橫梁各修改方案

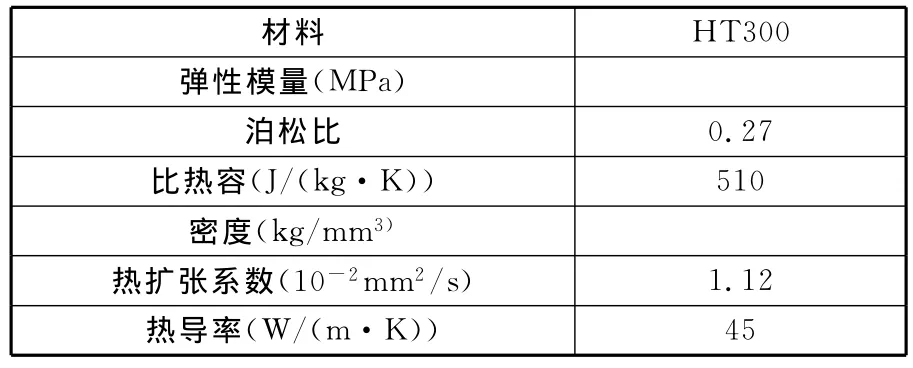
表2 材料特性數據

在進行約束模態分析時，對每種方案加固定約束；在自由模態分析中不加任何約束。在進行靜力分析時，滑塊安裝面除了受床鞍傳來的磨削力外，還受床鞍及主軸部件的重力作用，其受力情況如表3所示。

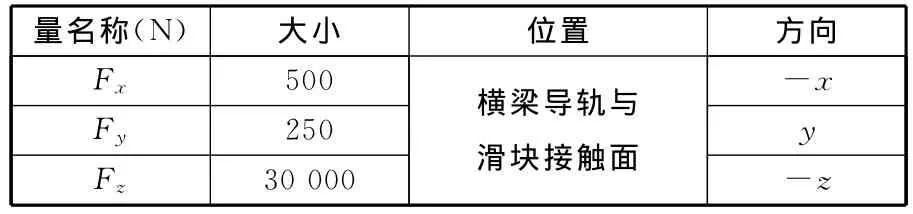
表3 橫梁受力情況

在進行熱分析時，由于滾珠絲杠軸承發熱，在軸承安裝面上加150W的熱流量，其余面上的空氣對流系數設置為5W／（m2·K）。橫梁受力分析結果如表4所示。

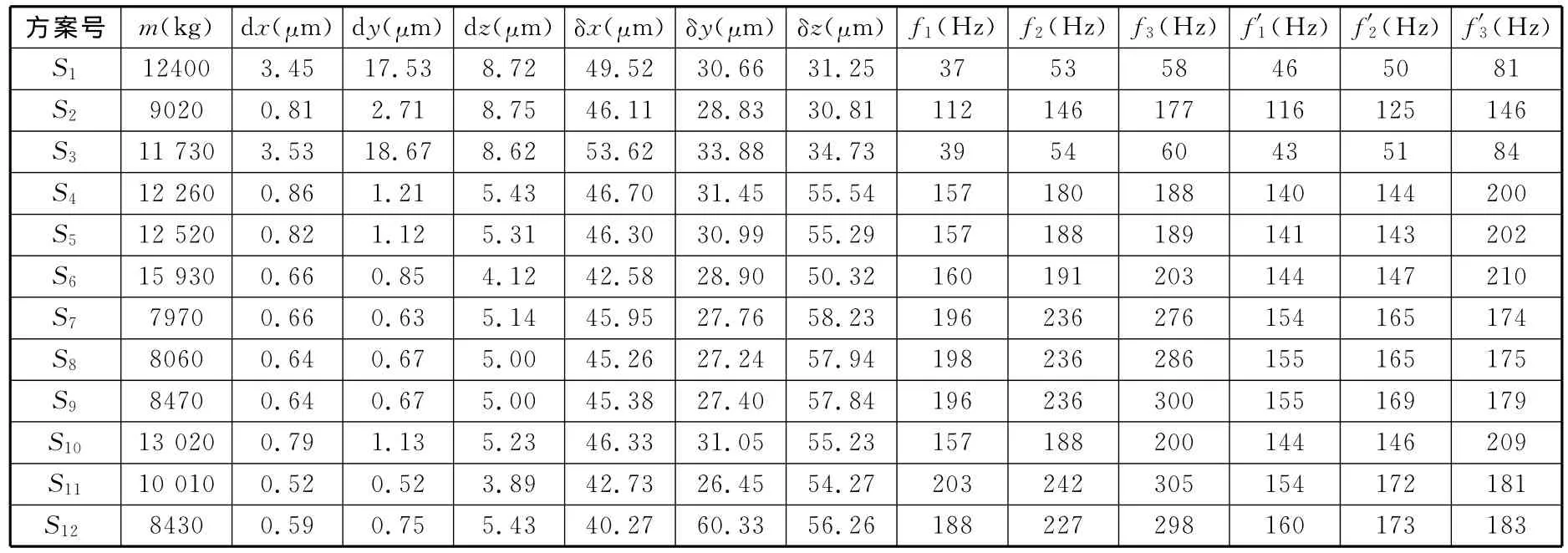
表4 橫梁受力評價指標

5.2 橫梁評價指標權重系數分配

根據綜合評價因素集確定的各個評價指標的權重系數如表5所示。

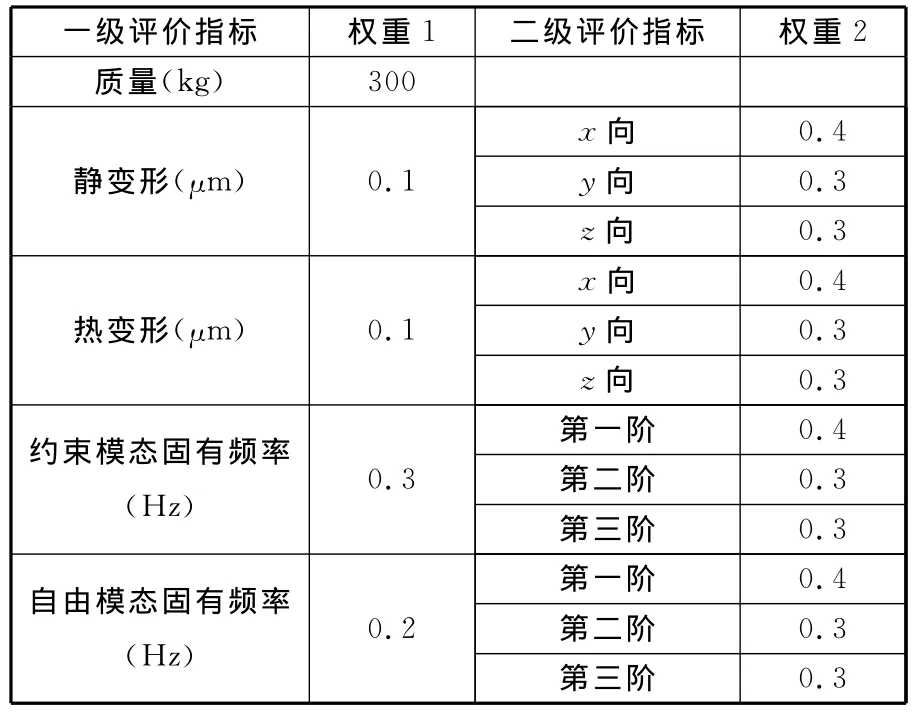
表5 橫梁各評價指標權重系數分配

算得 W＝｛0.3，0.04，0.03，0.03，0.04，0.03，0.03，0.12，0.09，0.09，0.08，0.06，0.06｝，然后分別根據前述三種綜合評價方法進行計算。

5.3 TOPSIS評價

首先根據表4列出特征矩陣，然后根據特征矩陣計算得出規范化矩陣R（由于矩陣尺寸過大，在此不予列出）。

由式（7）及式（8）計算理想解和反理想解：

根據式（8）及式（9）計算歐幾里德距離：

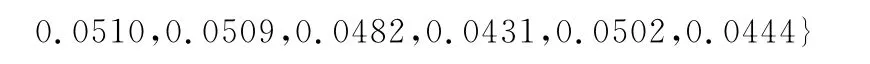
最后由式（7）算出每種方案指標距離理想解的貼近度：

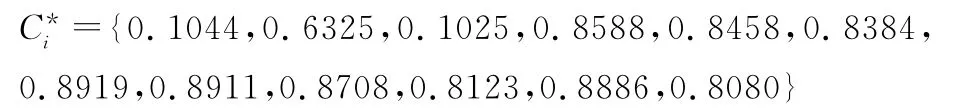
同理，利用式（10）、式（11）和式（7）可得到各方案的基于蘭氏距離的貼近度：

利用式（12）、式（13）和式（7）可得到各方案基于相似距離的貼近度：

5.4 TOPSIS評價法中不同距離尺度的比較

本文采用三種方法對12種橫梁結構方案進行評價。TOPSIS法強調在距離理想解近的同時要遠離負理想解，值越大表示離正理想解越近而離負理想解越遠，其最大的優點是簡單、直接，缺點主要是結果不具確切含義僅表示一種相對水平。

三種評價方法評價的結果如表6所示，分別用大于0.85，0.80，0.75的區分度值截取三種方案的選擇結果，得出的滿足條件的子集合為

其子集的交集為

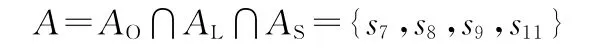
表6 三種距離尺度的TOPSIS評價方法比較

三種方法評價結果的區分度曲線如圖3所示。對于TOPSIS法，區分度值表示貼近度值。

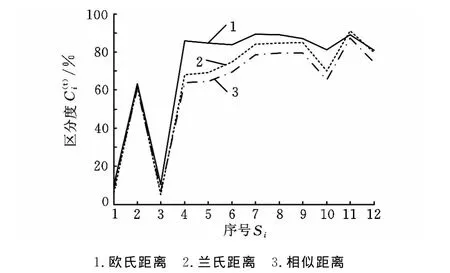
圖3 三種方法評價結果的區分度曲線

從交集結果及圖3中的三條曲線可以看出，對于不同的評價方法，最終方案排序結果總體一致，尤其是蘭氏距離法和相似距離法完全一致，均能得到滿意結果。但三種方法對各個方案區分的明顯程度不同，歐氏距離尺度法最差，蘭氏距離尺度和相似距離尺度均較為理想。因此，基于相對距離的蘭氏尺度和相似尺度法要優于基于絕對距離的歐氏尺度法。

6 結語

本文通過實驗和仿真驗證發現，歐氏距離尺度法、蘭氏距離尺度法和相似距離尺度法都能區分方案的優劣，但由于數據處理方法和區分度的定義不同，每種方法所選擇的最優結果仍有細微差別。三種方法所選的最優方案之間的改進度不大，其值在1%～5%之間。從各種方法對各個方案區分的明顯程度看，蘭氏距離尺度法和相似距離尺度法都優于歐氏距離尺度法。在實際設計生產中，采用蘭氏距離尺度法和相似距離尺度法的TOPSIS法都能快速合理地進行方案優選。

［1］陳永亮，耿文軒，滿佳，等.基于結構配置與性能改進綜合評價的機床結構適應性設計［J］.中國機械工程，2009，20（9）：1029－1033.Chen Yongliang，Geng Wenxuan，Man Jia，et al.Adaptable Design of Machine Tool Structure Based on Quantification of Structural Configuration and Performance Improvement［J］.China Mechanical Engineering，2009，20（9）：1029－1033.

［2］滿佳，張連洪，陳永亮.基于元結構的機床結構可適應優化設計方法［J］.中國機械工程，2010，21（1）：51－66.Man Jia，Zhang Lianhong，Chen Yongliang.An Adaptable Optimization Design Method of Machine Tool Structures Based on Unit Structure［J］.China Mechanical Engineering，2010，21（1）：51－66.

［3］王艷輝，伍建國，繆建成.精密機床床身的模態分析與結構優選［J］.機械設計與制造，2005（3）：76－77.Wang Yanhui，Wu Jianguo，Miao Jiancheng.Modal Analysis and Structure Optimization for Precision Machine Tool Bed［J］.Mechanical Design and Manufacture，2005（3）：76－77.

［4］尹紅.基于FEA的高速龍門加工中心橫梁部件的熱態特性分析與優化［J］.制造技術與機床，2011（9）：65－71.Yin Hong.Thermal Analysis and Optimization of High Speed Machining Center Beam Component Based on FEA［J］.Manufacturing Technology ＆Machine Tool，2011（9）：65－71.

［5］畢威寧.結合AHP與TOPSIS法于供應商績效評估之研究［J］.科學與工程技術，2005，1（1）：75－83.Bi Weining.The Research of the Evaluation Performance of the Combination of AHP and TOP－SIS Method for the Supplier［J］.The Journal of Science and Engineering Technology，2005，1（1）：75－83.

［6］吳有龍，楊倍箕，林瑞源.應用灰關聯分析與TOPSIS方法于游戲廠商財務績效評估模式［J］.管理科學研究，2009，5（2）：23－24.Wu Youlong，Yang Beiji，Lin Ruiyuan.The Model of Applying Application of Grey Relational Analysis and TOPSIS Method to the Game Makers Financial Performance Assessment［J］.Research on Management Science，2009，5（2）：23－24.

［7］付巧峰.關于TOPSIS法的研究［J］.西安科技大學學報，2008，28（1）：190－193.Fu Qiaofeng.The Research of the TOPSIS［J］.Journal of Xi’an University of Science and Technology，2008，28（1）：190－193.

［8］Li Y，Xue D，Gu P.Prioritizing Design Candidates in Adaptable Design Using the Grey Relational Analysis Approach［C］／／Proceedings of the Third CDEN／RCCI International Design Conference.Toronto，Ontario，Canada，2006：93－101.

［9］Hwang C L，Yoon K.Multiple Attribute Decision Making［M］.Roca Raton，FL，United States of America：CRC press，2011.

［10］Johnson R A，Wichern D W.Applied Multivariate Statistical Analysis［M］.Pearon，United States of America：Pearson Education，2007.

［11］Gan Guojun，Ma Chaoqun，Wu Jianhong.Data clustering［M］.Philadelphia，PA，United States of America：SIAM，Society for Industrial and Applied Mathematics，2007.

［12］Zhou Meili.Principles and Practice of Similarity System Theory［J］.International Journal of General Systems，1994，23（1）：39－48.

［13］Zhou Meili.Analysis Method of Similarity and Differentiablity for Complex Systems［J］.Journal of System Science and Information，2005，3（2）：399－409.

［14］周美立.復雜機械產品系統差異性分析度量方法［J］.農業機械學報，2006，37（7）：129－132，137.Zhou Meili.Analysis and Measure Methods of Diversity for Complexity Mechanical Products Systems［J］.Transaction of the Chinese Society for Agriculture Machinery，2006，37（7）：129－132，137.