無刷直流電機單神經元自適應智能調速系統

魏巍WEI Wei

（大慶煉化公司電子商務部，大慶 163310）

（Daqing Refining &Chemical Company E-commerce Department，Daqing 163310，China）

0 引言

目前無刷直流電機（BLDCM）被廣泛應用，是因為它有許多優點，像：本身體積較小、功率密度較其他電機高、相對控制要簡單、動態性能較好。由于它的控制系統特點是非線性且多變量的，所以利用傳統的PID 控制算法達不到電機的高精度要求和運行；而對于像滑膜變結構、神經網絡及模糊控制等先進的控制算法實現起來更復雜。

本文在建立無刷直流電機雙環調速系統時采用單神經元自適應控制方法，在調節神經網絡參數上應用Hebb學習規則，同時此電機的反電勢應用分段線性法模擬其變化趨勢。由此搭建了雙閉環BLDCM 智能調速系統，仿真結果得出了此系統較其他系統抗干擾能力更強，有較強的隨動性。

1 無刷直流電機建模策略

全控橋式三相星型無刷直流電動機結構如圖1 所示[1][2]。每相的定子繞組與其相對應的電子開關線路中的功率開關器件相連。此結構類似一個“電動機系統”，其系統相當于是由電子開關線路、永磁式同步電機和位置傳感器構成的。

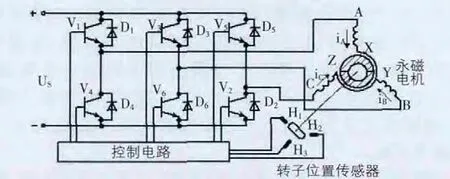
圖1 三相星型全控橋式BLDCM 結構圖

根據BLDCM 三相繞組的電壓平衡方程、運動方程和狀態方程，建立BLDCM 電機本體仿真模型如圖2 所示。

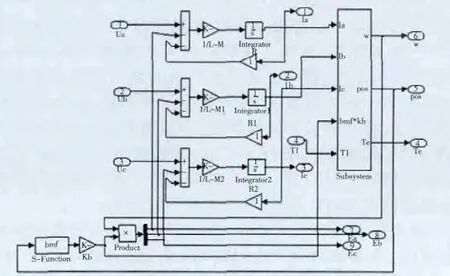
圖2 BLDCM 本體結構建模

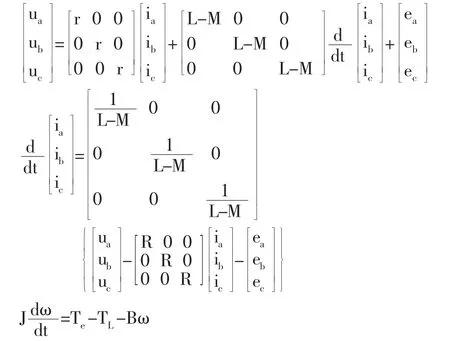
本文采用工作方式是每一瞬間有兩個功率管導通的梯形波電樞驅動電流。再應用分段線性法模擬梯形波的反電勢波形趨勢，通過將轉子的位置信號作為劃分運行周期的依據，把周期化為6 個階段，見圖3，以第一階段（0～π/3）為例：A 相反電勢為正向最大值Em，B 相為反向最大值-Em，而C 相則在換相階段。通過兩個信號變量分別是轉子位置和轉速信號來列出每一相反電勢變化趨勢的軌跡方程。

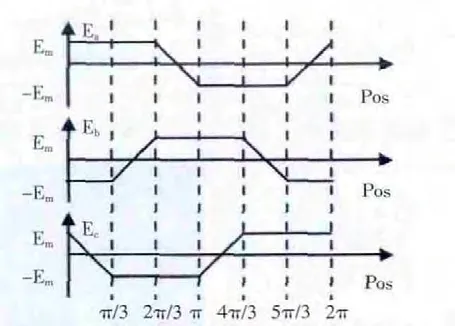
圖3 星形兩相導通六狀態BLDCM 反電動勢波形

表1 列出了轉子位置和反電動勢兩者之間的線性關系，k 為反電動勢系數；pos 為電角度信號；w 為轉速信號。

表1 轉子位置和反電動勢之間的關系表

2 控制策略與控制方法

利用滯環控制調節系統內環的電流，如圖4 所示，當系統反饋的瞬時電流值與設定的電流值做減法運算得到的數值等于滯環環寬的正向邊界時，VT1導通，VT4關斷，此時電動機與直流母線的正端接通，電流升高，相反的電流下降。為了實現實際電流跟蹤參考電流波形形成閉環控制，滯環的寬度選擇很重要。

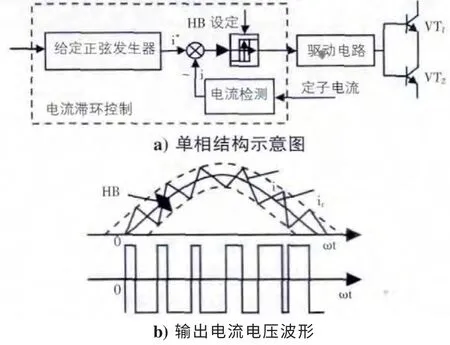
這里用單神經元自適應PID 控制系統外環[3][4]，圖5 為其結構圖，系統誤差、一級差分以及誤差累積做為單神經元的輸入量。

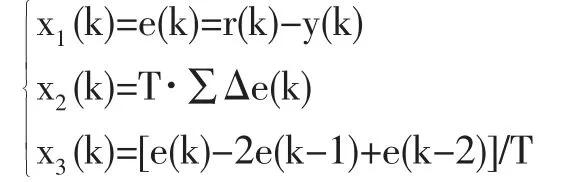
神經元通過關聯搜索，計算產生輸出信號u(k)為

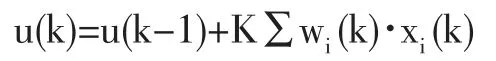
K 為調節環節放大系數，K 值過大會威脅系統的穩定性，而K 值過小，又會使降低系統的快速性，可見，K 值的選擇非常重要。本系統K 取值為2。

wi(k)為權系數，用Hebb 學習規則調整權系數，在線實時整定PID 控制的三個參數。

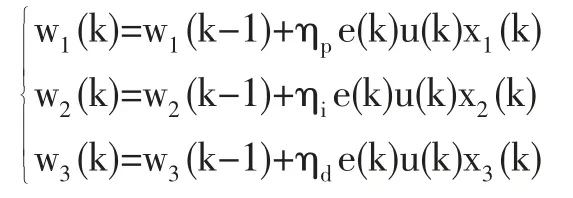
如果要分別調整不同的權系數就要用不同的學習速率，比例、積分、微分的學習速率分別用ηi、ηp、ηd表示。在每次采樣的同時都要依據反饋的誤差來對神經元的權值進行重新調整，本文ηi、ηp、ηd取為0.35，0.50，0.35；三個初始權值取0～1 之間的隨機數。

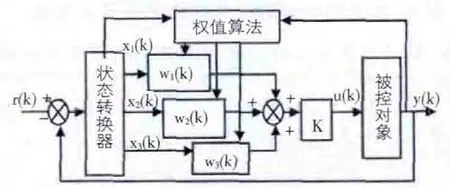
圖5 單神經元控制結構圖

由于e(k)和Δe(k)決定PID 參數的在線學習修正結果，所以想到了把xi(k)改為e(k)+Δe(k) 代入原來的PID 控制算法中的加權系數的學習修正部分，改進結果如下：

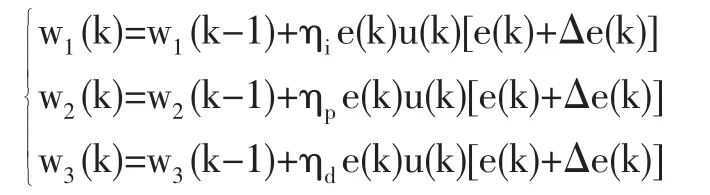
式中，Δe(k)=e(k)-e(k-1)。

3 系統建模

綜上所述，BLDCM 的控制系統框圖如圖6 所示。采用雙閉環控制方案，其中PI 調節器構成轉速環，電流滯環調節器構成電流環。

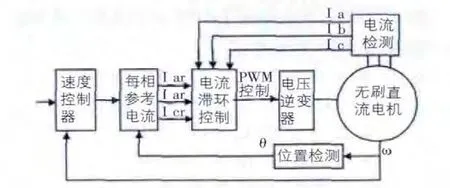
圖6 BLDCM 控制系統設計框圖

圖7 為系統總體仿真模型圖，由BLDCM 本體模塊、速度控制模塊、參考電流模塊、電流滯環控制模塊、轉矩計算模塊和電壓逆變器模塊構成。

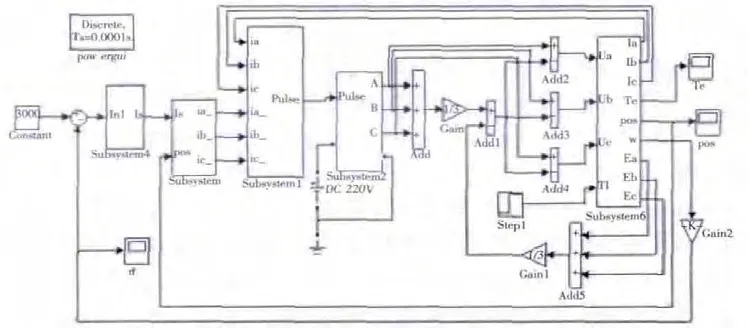
圖7 BLDCM 控制系統建模

圖8 為滯環控制模塊，三相的參考電流和實際電流作為輸入量，PWM 逆變器控制信號作為輸出量。從參考電流模塊那輸出三相的參考電流，表2 列出了轉子位置和三相參考電流之間的對應關系。

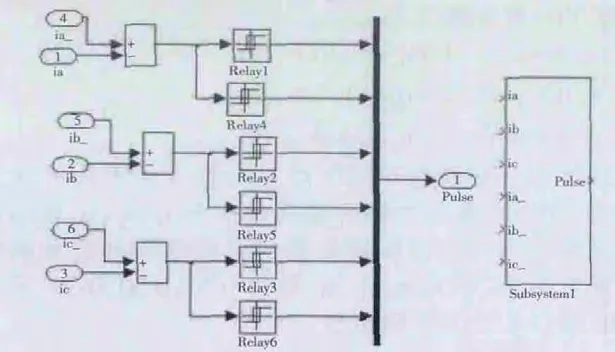
圖8 電流滯環控制模塊結構框圖及其封裝

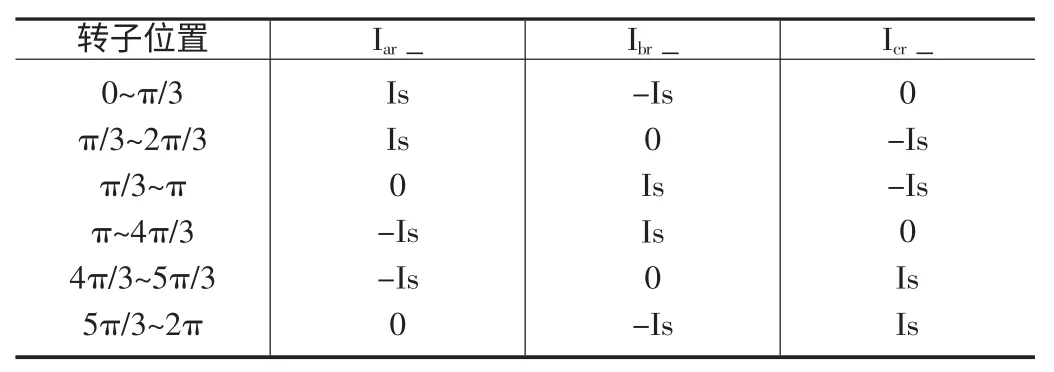
表2 轉子位置和三相參考電流之間的對應關系表

本系統采用常規PID 和單神經元自適應PID 兩者分別作為速度環控制器構成速度環控制模塊。單神經元自適應PID 控制器模型如圖9 示。

圖9 單神經元自適應PID 控制器模塊及其封裝

4 系統仿真及實驗驗證

選擇BLDCM 電機參數為：定子相繞組電阻R＝1Ω，定子相繞組自感L＝0.02H，互感M＝-0.061H，轉動慣量J=0.005kg·m2，反電勢常數Ke=0.185V·s/rad，阻尼系數B=0.0002N·m·s/rad，額定轉速n=1000r/min，極對數p ＝1，220V 直流電源供電，峰值電流35A。

系統進行空載啟動，達到穩態后，負載TL＝2.5N·m 在t＝0.7s 時加進系統，又在t＝1.4s 時從系統中撤去負載，最后得到三相電流、三相反電動勢、轉子位置信號和PWM 脈寬調制信號的仿真波形如圖10 所示。

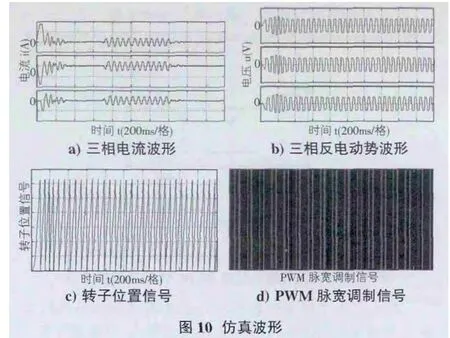
結果分析，空載運行時電流為零，電流在加上負載后迅速增加接近穩態，還可以看出方波電流波形的平頂部分因為換向而引起脈動。三相反電勢波形平頂部分約為120°。

采用常規PID 和單神經元自適應PID 兩者分別作為速度環控制器構成速度環控制模塊，轉速設定為1000rpm，系統同樣空載啟動，負載轉矩TL＝2.5N·m 在t=1s時加入系統，對比兩種不同算法的速度響應仿真曲線波形如圖11 所示。從圖可知，系統在常規離散PID 控制下，大約用了0.45s 的時間從系統啟動到進入穩態，而且有較大的超調量，約為40%；轉速在t＝1s 時發生突降，經過控制器的調節作用，大約經過0.35s 后，系統再次恢復到平衡狀態。相比之下，應用單神經元自適應PID 控制，系統在很短的時間內就進入到了穩態，超調量遠遠小于前者，僅為1.5%；轉速在t＝1s 時加入負載時只出現了很小的波動，就迅速恢復到平衡狀態。

圖11 1000rpm 下轉速響應曲線

圖12 為系統在常規離散PID 和單神經元自適應PID控制下的轉矩輸出響應曲線。和常規PID 控制相比，單神經元自適應PID 控制下的轉矩波動較小。

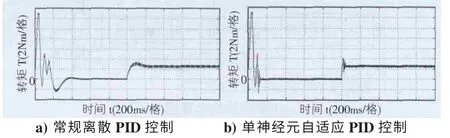
圖12 轉矩響應曲線

5 結論

本文基于BLDCM 電機建立的單神經元自適應PID智能調速系統具有較強的跟隨性、抗擾性和魯棒性，這些方面都遠遠優越于常規PID 控制器，單神經元自適應PID控制器之所以具有很強的參數適應性和魯棒性，動態響應快等優點，是因為它不受系統參數變化的影響，只需要考慮系統的輸入和輸出的變化就可以。可見，該系統還可以控制一些高性能的調速系統，具有廣泛的應用前景。

[1]張琛.直流無刷電動機原理及應用[M].北京:機械工業出版社，2004.

[2]卿啟新,葉漢民,楊曉武,時曉霞.基于模糊RBF 神經網絡的無刷直流電機調速控制[J].化工自動化及儀表,2010,37（7）：84-86.

[3]付華，馮愛偉，徐耀松等.基于單神經元控制器的異步電動機矢量控制[J].中國電機工程學報，2006，26(1):127-131.

[4]代睿,曹龍漢,何俊強,唐超,劉小麗.基于微粒群算法的無刷直流電機單神經元自適應控制[J].電工技術學報,2011,26(4):57-63,70.