應用于天線座的并聯機構構型設計*

□ 段艷賓 □ 賈彥輝 □ 李建軍 □ 陸海坤

1.中國電子科技集團公司 第五十四研究所 石家莊 050081

2.河北遠東通信系統工程有限公司 石家莊 050081

隨著射電天文技術的發展，對射電天文望遠鏡天線的精度、速度等要求越來越高。由于傳統方位俯仰天線座和XY型天線座存在如結構復雜、體積質量大、在天線連續轉動時必須要有匯流環和關節、且存在跟蹤盲區等缺點［1、2］，精度和速度越來越成為制約射電天文技術發展的主要因素，因此迫切需要在天線座架結構和控制上進行創新。在這些方面并聯機構天線座有其自身的優點［3-5］，主要體現在：機械零部件主要由滾珠絲杠、虎克鉸、球鉸、伺服電機等標準通用元器件組成，其數目較串聯機構大幅減少，因此結構簡單，可靠性高；結構剛度大，承載能力強，靜態誤差小，剛度重量比遠高于傳統的方位俯仰天線座；各可伸縮桿桿長均能單獨對動平臺的位置和姿態起作用，不存在傳統天線座的幾何誤差累積和放大的現象，甚至還有平均化效果，加之結構的對稱性，故運動精度高；六桿天線座在天線連續轉動時不需要匯流環和關節，且不存在跟蹤盲區。

基于并聯機構的種種優點，國內外學者開始研究將并聯機構應用于天線座架［6］，以提高射電天文望遠鏡天線的運動速度和精度。

國內如華為實［7］研究了Stewart并聯機構作為天線支撐的分析，鄧先榮［8］在Stewart并聯機構對雷達領域的應用進行了探討，關貴注［9］等將并聯機構應用于跟蹤天線座進行了系統設計。但他們僅僅是將并聯機構作為天線、雷達支撐的可行性進行了分析，并未對并聯機構應用于天線支撐所存在的問題進行深入探討。

筆者從實際設計角度出發，分析了影響Stewart并聯機構作為天線座架的因素，提出了切實可行的設計方法，對并聯機構應用于天線系統有重要參考意義。

1 構型設計影響因素

1.1 結構簡介

如圖1所示，Stewart并聯機構由上下平臺以及6條可伸縮支鏈組成，支鏈一端通過虎克鉸與上平臺連接，另一端通過球鉸與下平臺連接，影響其構型參數的主要有 R、r、H、θ1、φ1和 θ2、φ2。 其中 R 為固定平臺上各鉸點所在圓周半徑；r為運動平臺上各鉸點所在圓周半徑；H為動定平臺鉸點中心之間的距離；θ1、φ1為固定平臺相鄰兩鉸點間夾角；θ2、φ2為運動平臺相鄰兩鉸點間夾角。

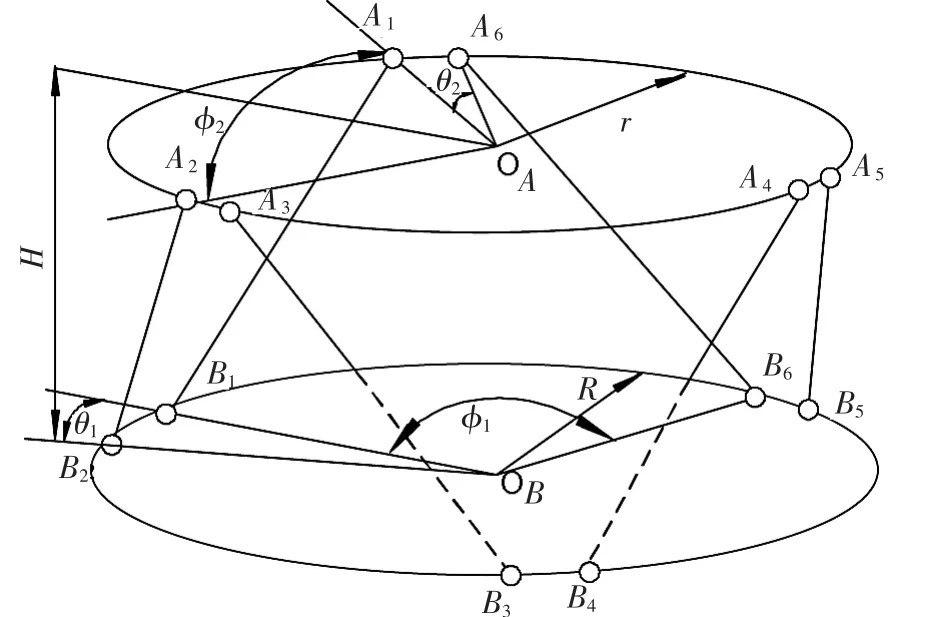
▲圖1 Stewart并聯機構結構示意圖

1.2 影響Stewart并聯機構功能工作空間的因素

1.2.1 桿長的限制

定義動平臺的3個歐拉角為α、β、γ，則從動平臺到定平臺的姿態變化矩陣為：

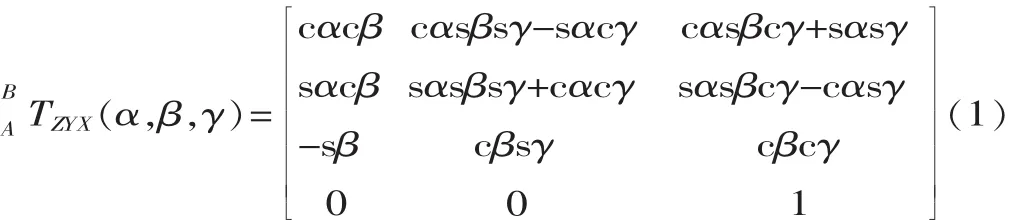
式中：cα=cosα，cβ＝cosβ，cγ=cosγ，sα=sinα，sβ＝sinβ，sγ=sinγ。

定平臺上各虎克鉸中心在定坐標系中的坐標為：

動平臺上各球鉸中心在動坐標系中的坐標為：

將動平臺上各球鉸中心在動坐標系中的坐標轉化為在定坐標系中表示：

根據6個驅動桿的球鉸中心點坐標和虎克鉸中心點坐標，即可求得各驅動桿長度li：

式中：li為各驅動桿長度。

式（5）為并聯機構給定運動平臺的位置和姿態后各分支桿所需要的桿長，但是桿長的長度變化范圍是有限的，這里用lmin和lmax來表示第i個分支桿運動范圍的最小值和最大值，則桿長的約束可以用，lmin≤li≤lmax表示，當某一桿長長度達到其極限時，運動平臺上給定的參考點也就到達了工作空間的邊界。

1.2.2 運動副轉角的限制

機構上平臺與各分支桿相連的關節為球面副，而下平臺與各分支桿相連的關節是虎克鉸，球面副和虎克鉸的轉角范圍實際上是有限制的。

如圖2所示，球面副的轉角θ由球面副基座的坐標系Z軸和球面副的向量u確定，可以看出，球面副和虎克鉸的最大轉角θmax與運動副的具體結構有關。若第i個球面副的基座在坐標系｛A｝中的姿態用向量nAi來表示，則球面副的轉角約束：

▲圖2 球面副結構示意圖

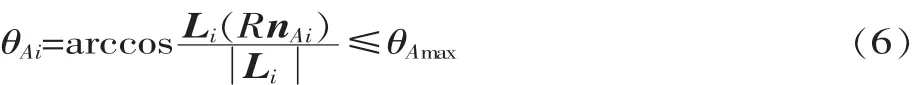
同樣，虎克鉸的轉角約束：

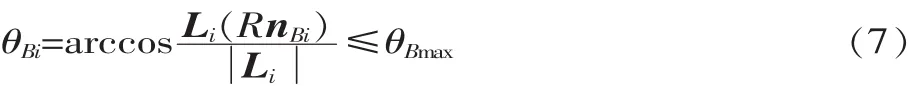
對于Stewart機構而言，影響其工作空間的主要因素為鉸鏈的轉動范圍和桿長的限制，除此之外還有連桿之間的干涉、連桿與上平臺之間的干涉等，這些需要在機械設計時加以注意。

2 構型優化

2.1 優化原則

由于六桿機構所涉及的參數較多，需要根據不同的應用場合制定合適的構型優化原則。

六桿機構應用于天線座，主要關心的是天線的方位、俯仰角度，天線需要方位360°旋轉，俯仰角度為0～90°。因此六桿機構的優化原則首先是方位、俯仰角度都能到達指標要求。在指標達到要求的前提下，虎克鉸、球鉸所需的轉動范圍越小越好，且分支桿行程合適，在此基礎上，分支桿的受力越小越好。故提出以下優化原則。

（1）方位、俯仰范圍分別為 0～360°和 0～90°。

（2）在機構工作空間內，虎克鉸、球鉸運動范圍在鉸鏈設計范圍之內。

（3）分支桿所需行程在安裝范圍內。

（4）在全工作空間內，分支桿所受力較小。

2.2 天線方位俯仰轉角與鉸鏈擺角及桿長關系

在轉動方面，六桿機構有其獨特的優勢，如圖3所示，圖中，OA為動平臺中心，OB為定平臺中心，天線轉動中心可以任意指定，即天線可以繞OA轉動，也可以繞OAOB之間的任意點轉動，如圖3所示的O點。

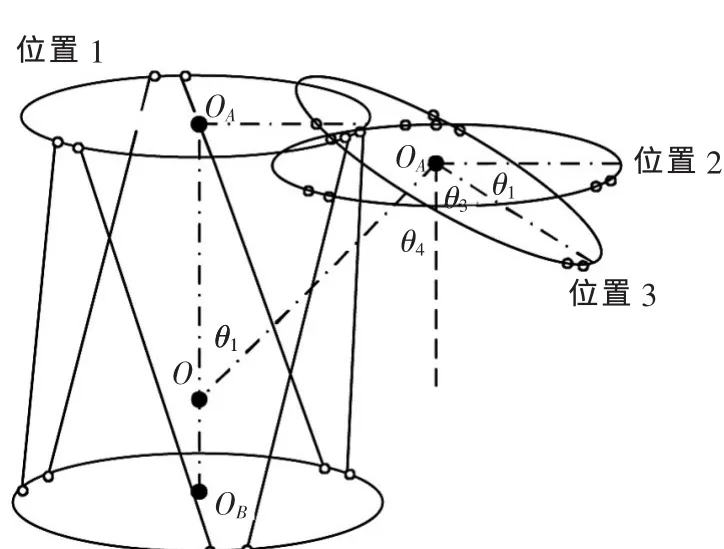
▲圖3 運動平臺轉動示意圖

從圖3可得出，動平臺繞O轉動θ1可以看作動平臺先從位置1平移到位置2，再繞OA轉動θ1，也就是說動平臺繞O轉動θ1時，與動平臺直接繞OA轉動θ1指向一致，只是動平臺中心點OA發生了變化。

因此，在俯仰控制時，控制思路為：上平臺先繞中心點O轉動θ1，再繞動平臺中心點OA轉動到90°。

根據以上分析，當機構構型確定后，影響機構轉動能力的因素主要為虎克鉸、球鉸轉動范圍以及桿長行程。三者主要與以下兩個參數有關。

（1）轉動中心位置O。

（2）繞轉動中心O轉動角度θ1。

給定 R=725 mm、r=450 mm、H=2 900 mm，θ1=θ2=20°、φ1=φ2=100°。

根據結構構型以及桿長和鉸鏈公式，按照上述控制思路，編程求取機構在全工作空間內運動過程中桿長最大行程及鉸鏈的轉動角度。

圖4～圖6中，橫坐標為轉動中心O距動平臺距離，即OOA值；縱坐標分別為分支桿行程、鉸鏈擺角等；不同直線表示不同θ1時分支桿行程、鉸鏈擺角與OOA關系。

從圖4中可以看出，當θ1一定時，分支最大行程隨OOA增大而增大；從圖5中可以看出，當θ1一定時，球鉸所需最大擺角隨OOA增大而減小；從圖6中可以看出，當θ1一定時，虎克鉸所需最大擺角隨OOA增大而增大。θ1的值只是影響直線的斜率。

從圖5中可以看出，在OOA和θ1均為0時，球鉸最大擺角最大，已超過90°，而與之對應的虎克鉸最大擺角較小，一般情況下，所設計的鉸鏈最大擺角不超過90°，因此需要選擇合適的OOA和θ1，使鉸鏈最大擺角在所設計的范圍內。

從圖4、圖5可知，OOA的值選擇在H（動定平臺之間距離）一半左右比較合適，因為此時分支桿行程增加較小，而所需球鉸最大擺角下降較大。

▲圖4 分支桿行程與轉動中心及轉動角度關系

▲圖5 球鉸最大擺角與轉動中心及轉動角度關系

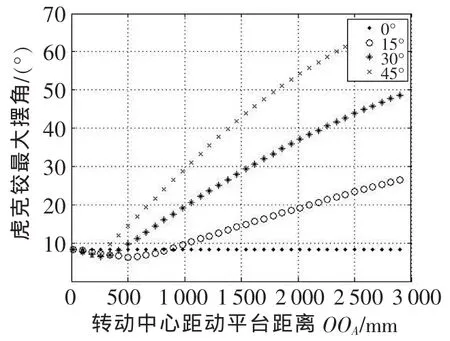
▲圖6 虎克鉸最大擺角與轉動中心及轉動角度關系

▲圖7 優化過程流程圖

綜合分析，暫定OOA=0.5H、θ1=30°進行Stewart并聯機構的結構優化設計。優化流程圖如圖7所示。

約束條件包括分支桿行程及安裝空間、鉸鏈擺角＜85°、鉸鏈安裝空間等。搜索范圍為：R=300 mm～700 mm，r=200 mm～400 mm，H=1 200 mm～2 500 mm，鉸鏈夾角范圍 4～20°。

經編程計算，得到合適的構型，見表1。

表1 優化所得機構參數表

根據表1中的參數，利用MATLAB編程計算機構在負載5 000 N、方位 360°、俯仰90°工作空間內運動以及末端速度 10°/s、加速度 20°/s2時，分支桿上鉸鏈轉動范圍、分支桿運動范圍、受力及速度加速度情況見表2。

從表2可以看出，所設計的機構鉸鏈運動范圍、分支桿運動范圍及分支桿速度、加速度、受力等均在可承受的合理范圍內，說明通過以上優化算法能夠優化出符合要求的并聯機構天線座架。

表2 運動過程中分支桿參數表

3 結論

本文以應用于天線座架的Stewart并聯機構為對象，研究了影響應用于天線座架的Stewart并聯機構的構型的主要因素，建立了構型的優化原則，得到了并聯天線座架方位俯仰轉角與機構鉸鏈擺角及桿長的關系，最后通過計算實例驗證了構型優化原則的正確性。本文緊密結合實際要求，研究內容對于Stewart并聯機構，真正應用于天線座架具有重要的理論指導意義。

［1］ 張燕.過頂跟蹤的天線座設計方法 ［J］.無線電工程，1997，27（4）:37-39.

［2］ 吳風高.天線座結構設計［M］.西安：西北電汛工程學院出版社，1975.

［3］ Stewart D.A Platform with 6-DOF ［C］.Proceeding of the Institution of Mechanical Engineering，London，1965.

［4］ 黃真,趙永生，趙鐵石.高等空間機構學［M］.北京：高等教育出版社,2005.

［5］ 韓秀英，劉延斌，賈現召.6-SPS型并聯機構的混合坐標動力學建模［J］.機械設計與制造，2008（1）:4-5.

［6］ 華為實.基于3—RSR并聯機器人機構的天線支撐 ［J］.機械，2000，27（5）:10-14.

［7］ 華為實.Stewart機器人用作天線支撐的分析 ［J］.電子科技大學學報，1999，28（4）:443-446.

［8］ 鄧先榮.Stewart平臺機構在雷達領域中的應用探討［J］.電子機械工程，2009,25（2）：41-43.

［9］ 關貴注，李涼海，張雪峰，等.六自由度自跟蹤天線座的系統設計［J］.遙測遙控，2007,28（11）：209-211.