結構因素對離心通風器性能影響的數值研究

徐讓書，邵長浩，牛 玲，常柱宇，簡 欣，李 駿

（沈陽航空航天大學 航空航天工程學部，沈陽，110136）

0 引言

離心通風器是航空發動機滑油系統的重要部件，其功用是回收滑油，一般回收率可達99%。離心通風器內部2相流動較為復雜，滑油以油滴、油霧和油膜3種形式存在[1]。氣相繞過油滴，在其表面形成附面層，顆粒后面會產生尾流。且油滴與油滴之間還會發生碰撞、聚合和破碎等現象，因此數值模擬要作適當簡化。與其他作用力相比，作用于連續相和分散相的重力影響均可忽略[2-3]。在離心力場中，大尺寸顆粒運動受自身慣性力作用，對氣流跟隨性較差[4]。文獻[5]介紹了2相流中液滴碰撞，沖擊和飛濺的數值模擬方法。蔣永松等運用數值方法對高壓風扇轉子進行研究，,指出葉尖附面層和泄漏渦對葉輪機械的影響[6]。離心通風器內切向速度在徑向上呈駝峰狀分布，即切向速度隨著半徑的減小而逐漸增大，到達一定程度后又會逐漸減小。通風器內靠近軸心某一半徑處存在1個邊界，這個特點與旋風分離器極為相似[7-8]。相關研究表明漩渦邊界有顆粒聚集的現象[9-10]。除了離心力和慣性分離對分離效果影響較大外，湍流彌散對提高分離效率也有重要作用，合理地提高湍流強度可以減少滑油消耗量[11]。分離器出口的速度分布均勻有利于上游的油氣分離[12]。Glahn[13-16]通過CFD方法預測滑油系統部件中的油氣2相流流動。

離心通風器輻板頂圓半徑的大小影響分離腔內氣流的切向速度分布，采用偏心式通風孔可以減小流道的流通阻力，改善下游速度場分布。本文以輻板頂圓半徑和通風孔偏心距為優化因素，應用計算流體力學軟件模擬二者對離心通風器分離效率和通風阻力的影響。

1 數值計算

1.1 結構及網格

離心通風器流道結構如圖1所示。通風器旋轉空心軸上的6個通風孔和12個輻板沿周向均布，計算結構具有良好的旋轉周期性，實際計算中取1/6圓柱區域進行網格劃分。通風孔上、下截面均采用interface，保證整體計算域內均為六面體網格。不同疏密度網格的計算結果表明，網格總數在約為90萬時，具有網格無關性。由于旋轉輻板毗鄰區、通風孔及其上下游區域壓力和速度梯度大，所以網格較為密實。通風器內腔采用沿徑向尺寸逐漸加大的漸變網格，以減小總體網格數量。壁面作邊界層處理，保證壁面在合理范圍內。

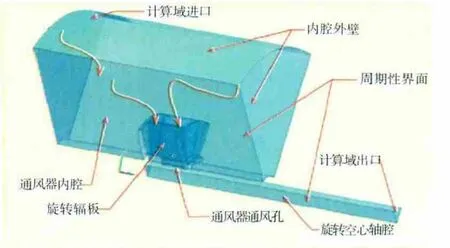
圖1 離心通風器流道結構

1.2 計算方法

采用耦合隱式求解器求解單旋轉坐標系下的3維N-S雷諾時均湍流方程。湍流模型采用雷諾應力（RSM）模型，采用相間耦合的DPM模型對離散相進行計算，采用隨機軌道（StochasticTracking）模型對湍流影響下離散相的運動軌跡進行追蹤。采用油滴顆粒碰壁機制，用壁面液膜模型（WallFilm）模擬油滴碰壁后的運動形式。空間離散格式為：壓力的離散采用PRESTO!格式；動量、湍流耗散率和雷諾應力采用QUICK格式；算法采用壓力與速度耦合。

1.3 參數的定義

離心通風器轉子某截面剖面如圖2所示。通風孔偏心距e 定義為通風孔中心線與空心旋轉軸中心線的空間距離；輻板頂圓半徑r定義為旋轉輻板頂圓跡線到空心旋轉軸中心線的空間距離。

離心通風器內部空氣溫度變化不大：馬赫數小于0.3；密度變化率很小，所以連續相按不可壓縮流動處理。空氣和滑油的物性參數見表1。

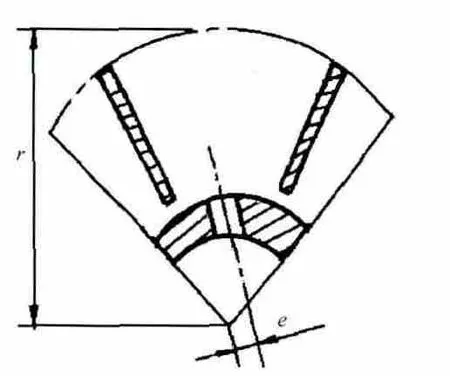
圖2 離心通風器轉子某截面剖面

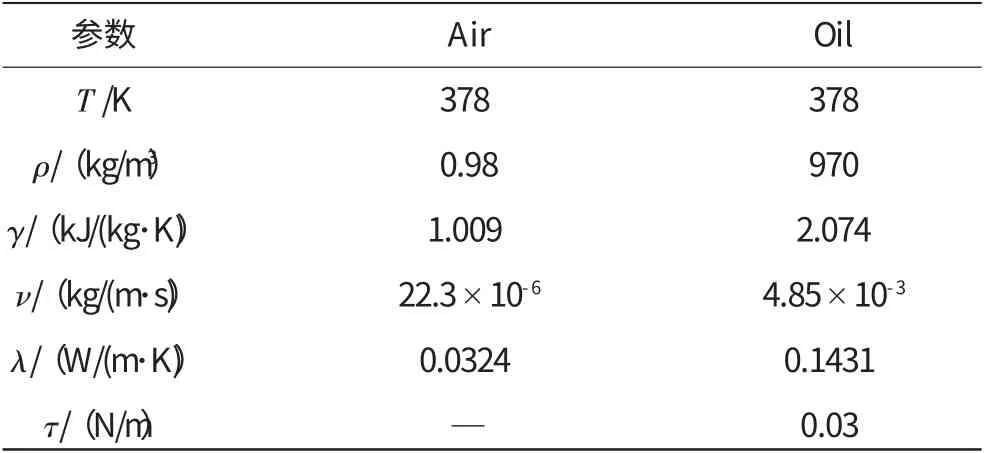
表1 空氣和潤滑油的物性參數

分離效率是評價通風器油氣分離性能的重要指標，表征通風器從流體中捕集油滴顆粒的能力。分離器的分離效率為2相流體通過通風器時所捕集的顆粒量占進入通風器的顆粒總量的百分數，以η 表示。

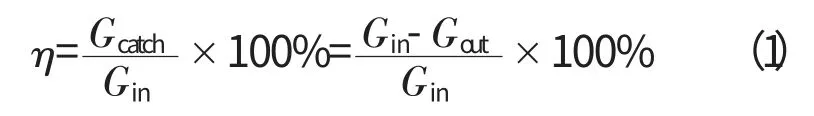
式中：Gin為進入通風器的顆粒量；Gout為從通風器排出的顆粒量；Gcatch為通風器所捕集的顆粒量。

除油氣分離外，離心通風器的另1個重要性能是其流動阻力，是影響發動機傳動腔內壓力的關鍵因素之一。阻力過大將嚴重影響通風能力，造成發動機傳動腔內壓力增高；阻力過小又會使傳動腔內壓力太低，造成封嚴裝置前后壓差加大，漏氣量增加。通風阻力定義為入口總壓Pin與出口總壓Pout的差值

1.4 邊界條件

計算域進口給定質量流率為0.005kg/s。通風器內腔和空心軸腔側壁按周期性邊界條件處理。內腔外壁面定義為固定壁面，其余壁面邊界定義為移動壁面（movingwall），運動方式定義為與相鄰單元區域相對旋轉速度為零，所有壁面剪切條件均為無滑移條件。壁面的DPM邊界條件采用壁面液膜（WallFilm）模型，模擬離心通風器內油滴顆粒與油膜的相互作用。取標準大氣壓力（101325Pa）為參考壓力。出口為壓力出口，靜壓（表壓力）Pgout=0Pa。入口與出口的DPM邊界條件為逃逸（escape）類型。單旋轉坐標系旋轉軸轉速為22727r/min。

1.5 離散相噴射源

DPM模型顆粒軌跡追蹤的初始條件定義了顆粒類型和顆粒群進入計算域時的初始位置、速度、尺寸、流量和溫度等。采用實心錐形噴射（solid-cone injection）模擬來自上游進入通風器的油滴顆粒群。噴射源的顆粒初始位置和速度的方向在一定的錐角范圍內隨機分布，即初始顆粒流的空間位置和速度分布是隨機的。入口油滴顆粒的尺寸分布如圖3所示。油滴顆粒群尺寸采用對數Rosin-Rammler分布函數，顆粒類型為惰性剛性顆粒，應用電子表格以數據庫的形式生成顆粒包文件。

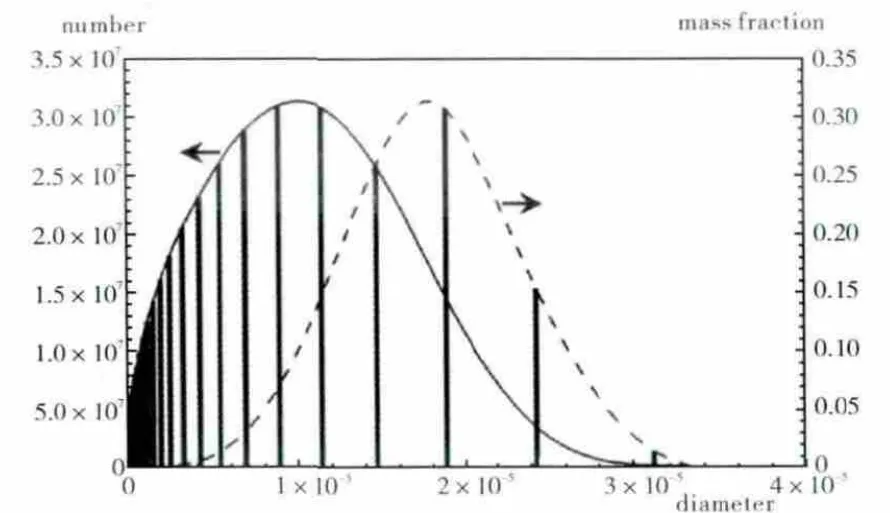
圖3 入口油滴顆粒的尺寸分布

2 結果分析

2.1 離心通風器內腔流體的渦結構分析

離心通風器內腔中的切向速度u 是油滴顆粒離心力的提供者，對油滴的分離起主導作用，表征氣流承載油滴顆粒運動的能力和對油滴顆粒形成離心效應的能力。u 在徑向上的變化非常顯著，但在運動半徑相同的圓周上切向速度數值變化很小。通風孔中心線上u 的計算值分布如圖4所示，離心通風器內腔中u 在徑向上呈駝峰狀分布，即切向速度隨著半徑的增加逐漸增大，到達某半徑處后又逐漸減小。離心通風器內腔的流場存在2個區域，如圖5所示。其中圖5（a）為似剛體旋轉區（強制渦），圖5（b）為勢流旋轉區（自由渦）。

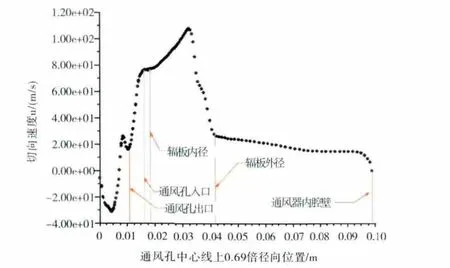
圖4 通風孔中心線上的切向速度u 的計算值分布

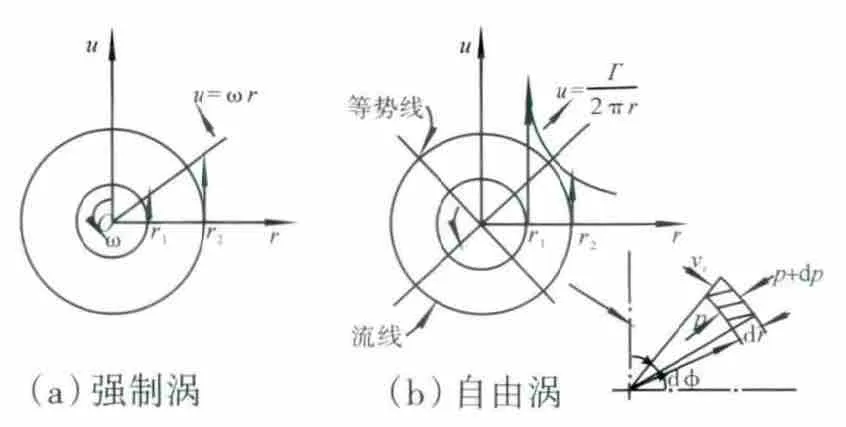
圖5 強制渦與自由渦

實際上，在通風器內氣流攜帶油滴顆粒運動過程中，流體具有黏性作用，與器壁之間存在摩擦力。因此，自由渦流體微團存在一定旋轉，故外渦流區稱為準自由渦區，這種旋轉對通風器內腔流場有一定影響。同樣，似剛體旋轉區的運動也受到黏性等因素的影響，因其速度分布與強制渦不同，稱為準強制渦。通風器內腔的組合渦如圖6中區域3所示，但是切向速度變化規律不符合組合渦的切向速度表達式（3），n值并不等于1或-1，也不符合動量矩守恒原則。

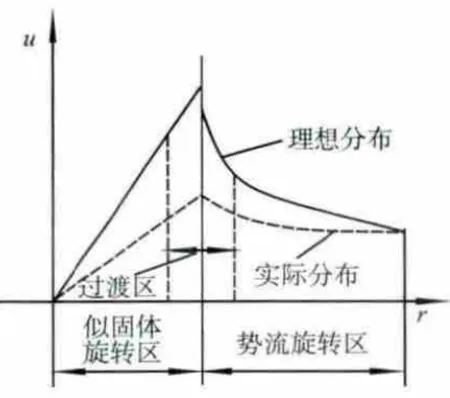
圖6 組合渦的結構

式中：n 和c 為與離心通風器工況、回轉半徑大小以及所在軸向位置相關的常數。

理想情況下勢流旋轉區n=1，似固體旋轉區n=-1。

2.2 分段分離效率

離心通風器的分段分離效率見表2、3。從表中可見，通風器內腔是主要的分離區域，分離效率一般為98%~99%。通風孔與空心轉軸段的分離效率很低，其分離效率不到總分離效率的1%。在分離過程中，較小顆粒隨氣流一起運動，一部分向下游遷移，一部分彌散于通風器內腔。較大顆粒受自身慣性力作用，可以脫離流線與壁面發生碰壁分離。在通風器內腔中，轉子帶動輻板高速旋轉，輻板頂圓半徑增加，使腔內油氣混合氣獲得更大的切向速度。因此，油氣混合氣的離心力更大，更有利于油滴的分離。

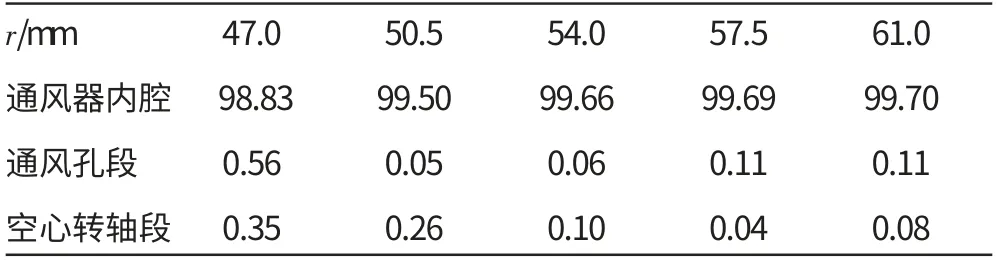
表2 不同輻板半徑下各段分離效率計算值 %

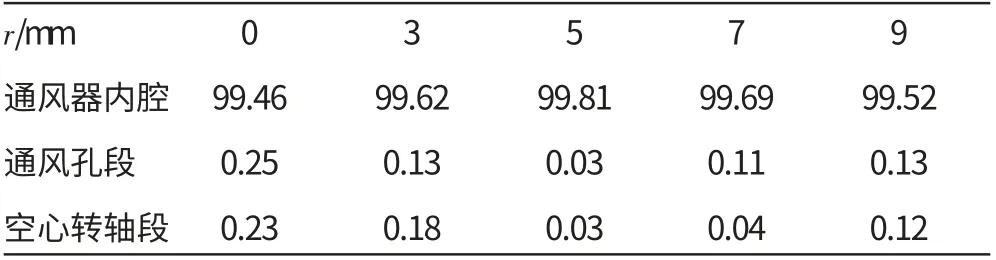
表3 不同通風孔偏心距下各段分離效率計算值 %

從表3中可見，通風孔偏心設計降低了通風孔段與空心轉軸段的分離效率。無偏心設計的2段分離效率之和為0.48%；偏心距為5mm時2段分離效率最低僅為0.06%。偏心通風孔設計降低了分離效率，明顯降低了流通阻力。

2.3 輻板頂圓半徑的影響分析

不同輻板頂圓半徑下的切向速度u的分布如圖7所示。增大輻板頂圓半徑r 可使通風器內腔流體與顆粒獲得更大的切向速度，流體的離心力也隨之增大，內腔中準自由渦區域空間體積沿徑向擴大，使油滴顆粒向壁面遷移的幾率增加，因此可提高分離效率η。

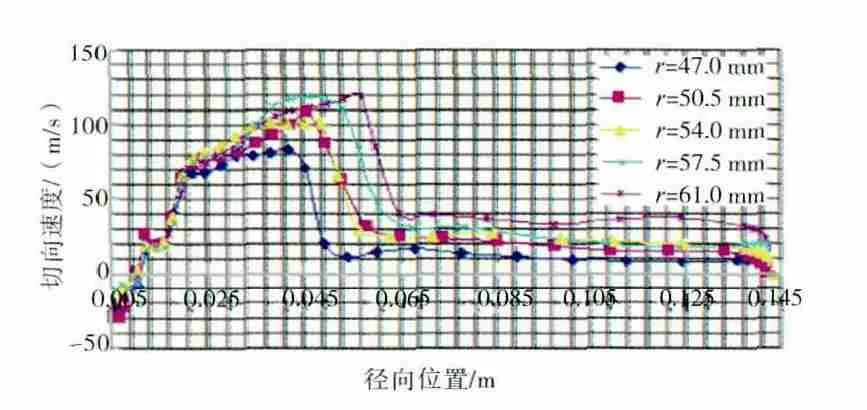
圖7 不同輻板頂圓半徑下的切向速度u 分布

不同輻板頂圓半徑下相關參數計算值見表4。從表中可見，η值在r=61mm時較r=47mm時高出0.15%，即增大輻板頂圓半徑可以提高離心通風器的分離效率。

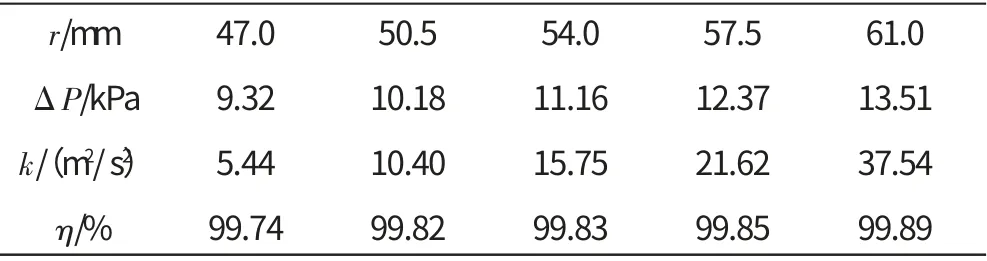
表4 e=7mm，不同輻板頂圓半徑下相關參數計算值

對表4的數據進行回歸分析，所得結果如圖8所示。其中Cal為計算值，Reg為回歸分析所得曲線。從圖8中可見，擬合曲線與計算值吻合較好；k 和η 均隨r 的增大而增加。說明湍流對油氣分離過程有較大影響，因此應加強通風器內腔的湍流強度。通風器內腔的湍流來源于高速旋轉的輻板對腔內氣體的攪動，旋轉空心軸腔中的湍流來源于從通風孔高速流入氣流的強烈擾動。改變旋轉輻板頂圓半徑會影響通風器內腔的湍流強度，但對其下游的旋轉空心軸腔內幾乎無影響。此外，通風阻力值隨r 的增大而增大。

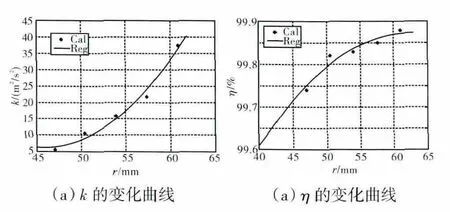
圖8 不同輻板頂圓半徑r 時k 與η 計算值的回歸分析

式（4）為k 與r 的擬合函數，函數的最大誤差為14.5%；式（5）為η 與r 的擬合函數，函數的最大誤差為0.3%。式（4）、（5）中r=47~61mm。

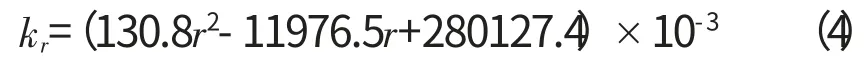
式中：kr為不同r 情況下的湍流動能擬合值。

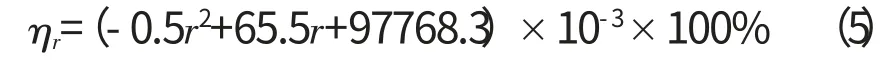
式中：ηr為不同r 情況下的油氣分離效率擬合值。

2.4 通風孔偏心距的影響分析

各種尺寸的滑油液滴顆粒隨氣流從通風孔進入旋轉空心軸腔內，首先沖向旋轉軸腔中心區。旋轉空心軸的高速旋轉帶來的切向速度使流體呈螺旋氣流向下游遷移，部分較大直徑的顆粒碰壁后黏附于壁面形成液膜；少數碰壁能量較大的顆粒發生散布或飛濺；其余主要集中在旋轉空心軸內表面附近。較小的顆粒隨空氣運動彌漫于空心軸腔內，較大顆粒與空氣的相對速度也較大，這反映在油滴顆粒雷諾數Rep分布上。不同e值時通風阻力、湍流強度和分離效率的計算值見表5。從表中可見，總分離效率η 隨e 的增加而降低，但幅度不明顯。其中，η值在無偏心距結構下要比e=9mm時多0.17個百分點。通風孔的偏心設計使氣流切向進入旋轉空心軸腔內，而不是直接沖向中心區，削弱了氣流的對心碰撞，使氣流的速度和壓力在徑向上均勻分布。這樣就減小了氣流的湍流強度，e=9mm相較于無偏心距時的湍動能減小3.91 m2/s2。此外，偏心通風孔減小了流道的通風阻力，保證了轉動腔內壓力。在e=0~7mm時，通風阻力隨e值增大逐漸減小，此后繼續增加e值，通風阻力基本不變。

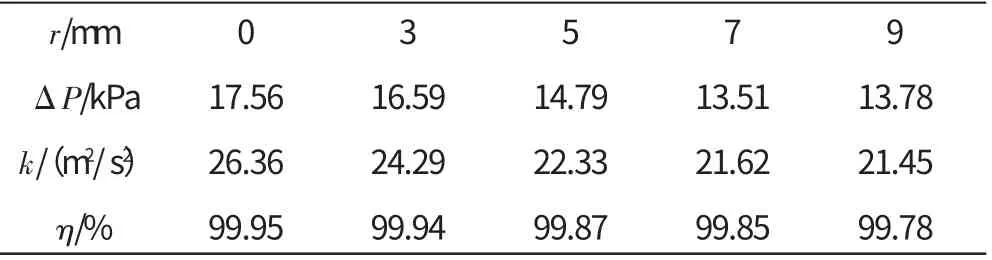
表5 r=57.5mm，不同通風孔偏心距下相關參數計算值

對表5的數據進行2次回歸分析，所得結果如圖9所示。從圖中可見擬合曲線與計算值吻合較好，完全符合計算值的趨勢。

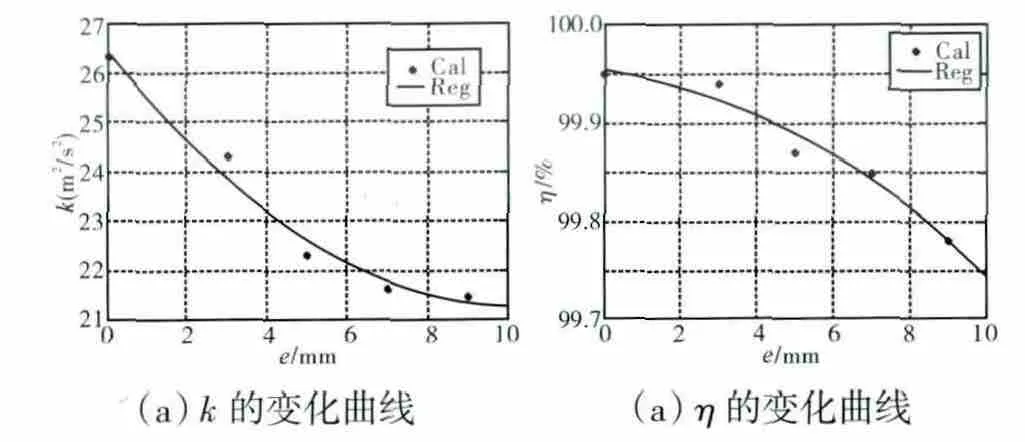
圖9 不同通風孔偏心距e 時k 與η 計算值的回歸分析

式（6）為k 與e 的擬合函數，其最大誤差為1.7%；式（7）為不同e 時的 擬合函數，其最大誤差為0.2%。式（6）、（7）中，e=0~9mm。

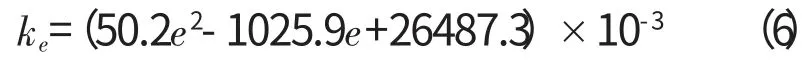
式中：ke為不同e值情況下的湍流動能擬合值。

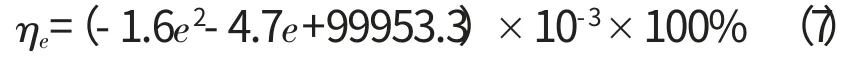
式中：ηe為不同e值情況下的油氣分離效率擬合值。

3 結論

本文應用DPM模型模擬通風器內油滴的運動軌跡，計算得到不同結構下離心通風器的腔內湍流強度、通風阻力與分離效率。所得主要結論如下：

（1）離心通風器內腔的切向速度u 在徑向上呈駝峰分布，與旋風分離器的很相似。

（2）分離效率受通風器內流體湍流影響明顯，并隨湍流強度增加而增大。

（3）在結構上增大輻板頂圓半徑，可以提高分離效率，但增加了流道結構的通風阻力。

（4）通風孔偏心設計可以減小通風器的通風阻力，并使出口的壓力和速度分布均勻，從而改善了出口流動狀態，但是降低了分離效率。

[1]Eastwick C N，Simmons K，Wang Y，et al.Study of aeroengine oil-air separators[J].Journal of Power and Energy，2006，220：707-717.

[2]Farrall M.Numerical modelling of two phase flow in a simplified bearing chamber[D].Nottingham,University of Nottingham，2000.

[3]馮健美，暢云峰，張勇，等.噴油壓縮機臥式油氣分離器特性的數值模擬及實驗研究[J].西安交通大學學報，2008，42（5）：561-577．FENG Jianmei，CHANG Yunfeng，ZHANG Yong，et al.Theoretical experimental research on oil-gas separator in compressor system [J].Journal of Xi’an Jiaotong University，2008，42（5）：561-577.(in Chinese)

[4]邵長浩，徐讓書.工況因素對離心通風器穿透率影響的數值研究[J].沈陽航空航天大學學報，2013，30（6）：8-10．SHAO Changhao,XU Rangshu.Numerical study on the effects of condition factors on centrfugal breather’s penetration[J].Journal of Shenyang Aerospace University,2013，30（6）：8-10.(in Chinese)

[5]Melbourne，Madrid，Cape T.Direct numerical simulations of gas liquip multiphase flows[M].NewYork：Cambredge University Press，2011：228-235.

[6]蔣永松，王詠梅，陳葆實.葉尖間隙對高負荷風扇轉子性能影響的數值研究[J].航空發動機，2006，32（4）：6-9.JIANG Yongsong，WANG Yongmei，CHEN Baoshi.Numerical investigation of tip clearance effects on the performance of high load fanrotor[J].Aeroengine，2006，32（4）：6-9.（in Chinese）

[7]柳吉祥.旋風分離器旋轉氣流特性分析[J].山東礦業學院學報，1988，7（3）：26-33．LIU Jixiang.Analysis on characteristic of the rotary flow in the cyclone separate[J].Journal of Shandong Mining Institute，1988，7（3）：26-33.(in Chinese)

[8]徐繼潤，羅茜.強制渦與水力旋流器[J].礦冶工程，1989，9（2）：29-33．XU Jirun，LUO Xi.Forced vortex and hydro cyclone[J].Mining and Metallurgical Engineering，1989，9（2）：29-33.(in Chinese)

[9]王兵，張會強，王希麟.顆粒在大渦結構中的彌散[J]．力學學報，2003，37（1）：105-109.WANG Bing，ZHANG Huiqiang，WANG Xilin. Particle dispersion in large eddy structures[J].ACTA Mechanica Sinica，2003，37（1）：105-109.(in Chinese)

[10]王兵，張會強，王希麟，等.湍流分離流動中的顆粒彌散機制[J].清華大學學報（自然科學版），2003，43（11）：18-36．WANG Bing，ZHANG Huiqiang，WANG Xilin，et al.Particle dispersion mechanism in turbulent separated flow[J].Journal of Tsinghua University（Science and Technology），2003，43（11）：18-36．(in Chinese)

[11]徐讓書，宗慶賀，劉立博，等.湍流彌散對軸心通風器油氣分離的影響[J]．航空發動機，2011，37（4）：5-9．XU Rangshu，ZONG Qinghe，LIU Libo，et al.Effect of turbulent dispersion on oil/gas separation process in axial ventilator[J].Aeroengine，2011，37（4）：5-9.(in Chinese)

[12]周華，夏南.油氣分離器內氣液兩相流的數值模擬[J].計算力學學報，2006，23（6）：767-771．ZHOU Hua，XIA Nan.Numerical simulation on the gas-liquid flows inside the oil-gas separators[J].Chinese Journal of Computational Mechanics，2006，23（6）：767-771．(in Chinese)

[13]Glahn A，Busam S，Blair M F，et al.Droplet generation by disintegration of oil films at the rim of a rotating disk[J].Journal of Engineering for Gas Turbines and Power，2002，124：117-124.

[14]Glahn A，Blair M F，Allard K L，et al.Disintegration of oil jets emerging from axial passages at the face of a rotating cylinder[J].Journal of Engineering for Gas Turbines and Power，2003，125：1003-1110.

[15]Glahn A，Blair M F，Allard K L，et al.Disintegration of oil films emerging from radial holes in a rotating cylinder[J].Journal of Engineering for Gas Turbines and Power，2003，125：1011-1120.

[16]Glahn A，Kurreck M，Willmann M，et al.Feasibility study on oil droplet flow investigations inside aeroengine bearing chambers-PDPA techniques in combination with numerical approaches[J].Journal of Engineering for Gas Turbines and Power，1996，118：749-755.