基于轉靜子耦合的組合壓氣機動力特性分析

漆文凱，王向輝

（南京航空航天大學能源與動力學院，南京210016）

0 引言

隨著航空技術的不斷發展，現代航空發動機的設計轉速越來越高，相應地機匣壁則設計得越來越薄，從而使發動機轉子、支承以及機匣之間的相互耦合日益加強，形成了復雜的結構動力特性。目前研究旋轉機械動力特性的方法主要有2大類，即傳遞矩陣法和有限元法。傳遞矩陣法因為編程簡單、計算速度快且有效而被廣泛應用[1-5]。隨著計算機技術的跨越式發展，大型商用有限元軟件的開發和不斷完善，有限元法以其計算精度高、數值穩定的特點，被越來越多的研究者所采用[6-9]。國內外已有很多學者對航空發動機轉子系統的動力特性進行了深入研究[1-9]，但考慮機匣與轉子耦合的研究還相對較少。文獻[10]基于NASTRAN中實體單元編制的轉子動力特性計算程序，對發動機整機進行了動力特性計算，并研究了考慮機匣振動耦合時轉子系統臨界轉速的確定方法；文獻[11]分別運用靜剛度、動剛度和整機有限元模型對某型發動機進行了轉子動力特性計算，并指出運用整機模型能夠充分考慮支承動剛度和各種機匣的局部振動對整機振動的影響；文獻[12]建立了1種新型的轉子-滾動軸承-機匣耦合動力學模型，利用數值積分方法獲取了系統響應，并研究了航空發動機的整機振動規律；文獻[13]針對實際的雙轉子航空發動機，建立了發動機雙轉子-支承-機匣耦合動力學模型，運用數值積分方法獲取系統非線性振動響應，研究耦合系統的動力特性。

本文以組合壓氣機為研究對象，考慮了轉子-支承-機匣系統的耦合效應，采用3維實體單元建模，利用有限元分析軟件ANSYS，對組合壓氣機進行動力特性分析。

1 組合壓氣機建模

由轉子動力學[14]可知，1個旋轉機械系統的運動微分方程式為

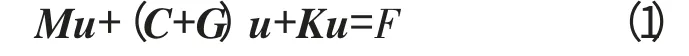
式中：M 為系統質量矩陣；C 為系統阻尼矩陣；G 為系統陀螺矩陣；K 為系統的剛度矩陣；u 為系統的位移響應矢量；F 為系統所受載荷；C，G 和u 分別為轉速的函數。

該方程的特征解和特征向量對應系統的固有頻率和振型，當轉速與系統的固有頻率相等時，該轉速即為系統的臨界轉速。

利用3維實體建模軟件UG建立機匣厚度為5、3和2mm的組合壓氣機模實體型，機匣厚度為3mm的組合壓氣機轉子模型和部件模型分別如圖1、2所示。

圖1 組合壓氣機轉子模型

圖2 組合壓氣機模型

該壓氣機由2級軸流式葉輪和1級離心式葉輪組成。在實體模型的基礎上，可以建立組合壓氣機轉子-支承系統(RBS)和轉子-支承-機匣系統(RBCS)的有限元模型，分別如圖3、4所示。其中，實體單元采用SOLID185單元，而支承部分則采用CONBINE14單元模擬，模型詳細參數見表1。

圖3 轉子-支承系統的有限元模型

圖4 轉子-支承-機匣系統有限元模型

2 轉子-支承系統動力特性分析

旋轉機械有1種特有的現象，即在轉速增大到某些特定轉速時，轉子的撓度會迅速增大，而當轉速超過該轉速時，撓度又迅速減小，這些特定的轉速稱為其臨界轉速。利用有限元分析軟件ANSYS對建立的組合壓氣機轉子-支承系統進行動力特性分析，繪制了該系統的Campbell圖，如圖5所示，并得到其前3階臨界轉速，見表2。由于同階正、反進動的振型一致，這里僅列出前3階正進動時的振型，分別如圖6~8所示。

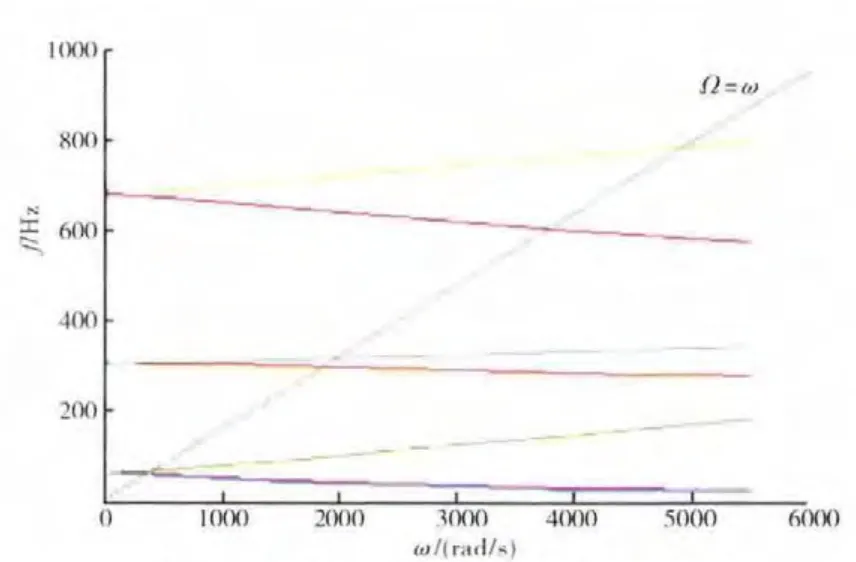
圖5 轉子-支承系統的Campbell

表2 轉子-支承系統的臨界轉速 rad/s

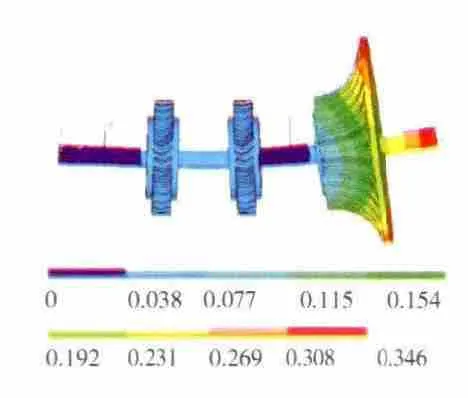
圖6 轉子-支承系統第1階正進動振型

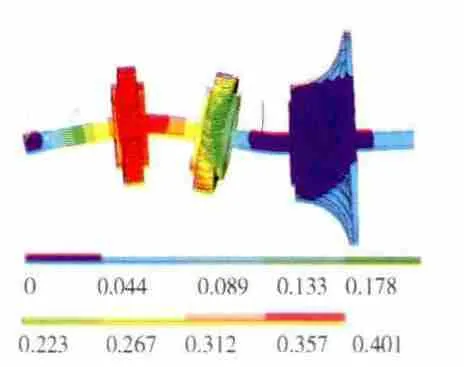
圖7 轉子-支承系統第2階正進動振型

3 機匣部件模態分析

航空發動機機匣作為發動機的承力機構，發揮著傳遞轉子載荷、包容轉子的重要作用，隨著機匣部件的日趨薄壁化，其振動特性也越來越復雜。現對厚度分別為5、3和2mm的組合壓氣機機匣部件進行模態分析，通過ANSYS軟件計算機匣部件前5階固有模態，得到其固有頻率及固有振型，其頻率見表3，由于3個模型的振型相同，限于篇幅，僅列出厚3mm的機匣部件的前5階固有振型，分別如圖9~13所示。

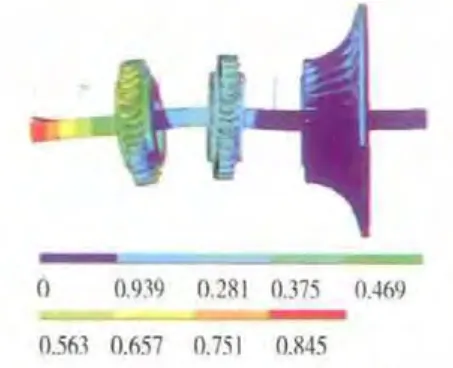
圖8 轉子-支承系統第3階正進動振型

表3 組合壓氣機機匣前5階固有頻率 Hz

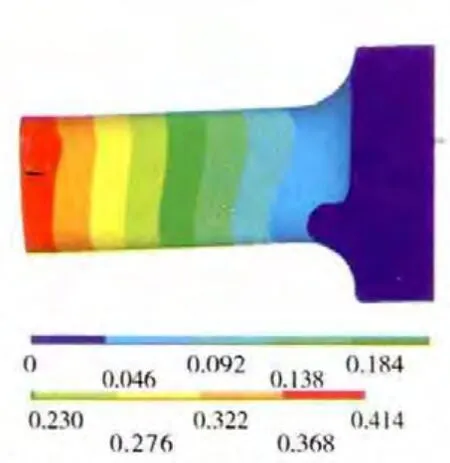
圖9 組合壓氣機機匣第1階振型

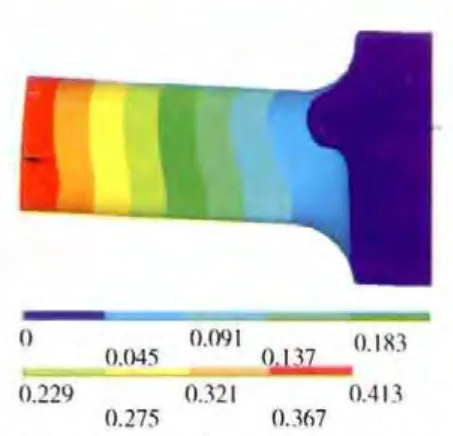
圖10 組合壓氣機機匣第2階振型

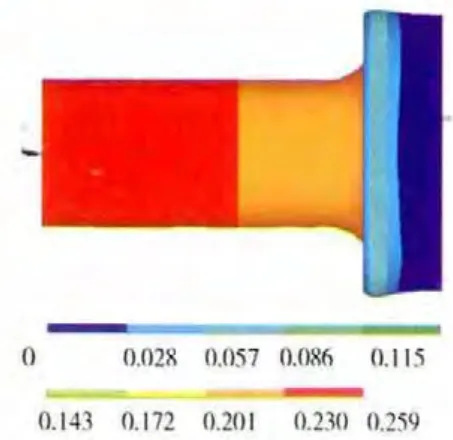
圖11 組合壓氣機機匣第3階振型

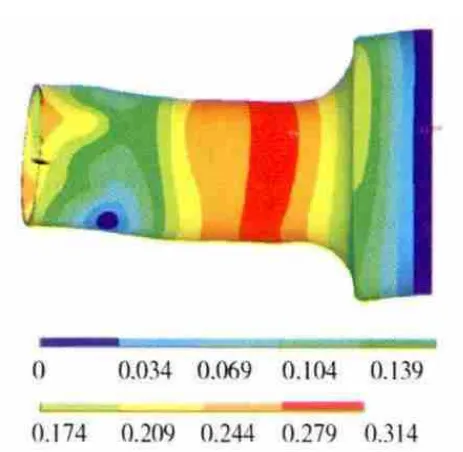
圖12 組合壓氣機機匣第4階振型

結合表3以及對應頻率的振型圖可見，第1、2階模態是機匣部件Z、Y 方向振動的第1階彎曲振動，第4、5階模態是機匣部件的第2階彎曲振動，而第3階模態則是機匣軸向伸縮振動。同時，從表3中可見，機匣部件的各階固有頻率隨著機匣厚度的減小而降低。

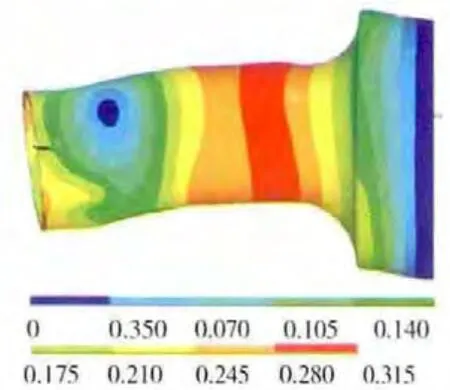
圖13 組合壓氣機機匣第5階振型

4 轉子-支承-機匣系統動力特性分析

機匣厚度的減小，其抗彎剛度也隨之降低，這對轉子系統的動力特性將產生很大影響。本文利用ANSYS軟件分別計算了機匣厚度為5、3、和2mm的組合壓氣機系統的前4階臨界轉速，并將其與轉子-支承系統的臨界轉速（同一轉子振型）對比，見表4，同時得到了對應轉速下的振型。限于篇幅，在此僅列出機匣厚度為3mm的組合壓氣機系統的正進動振型，分別如圖14~17所示。轉子-機匣系統也應給出Campbell，轉子-支承-機匣（3mm）系統Campbell如圖18所示。

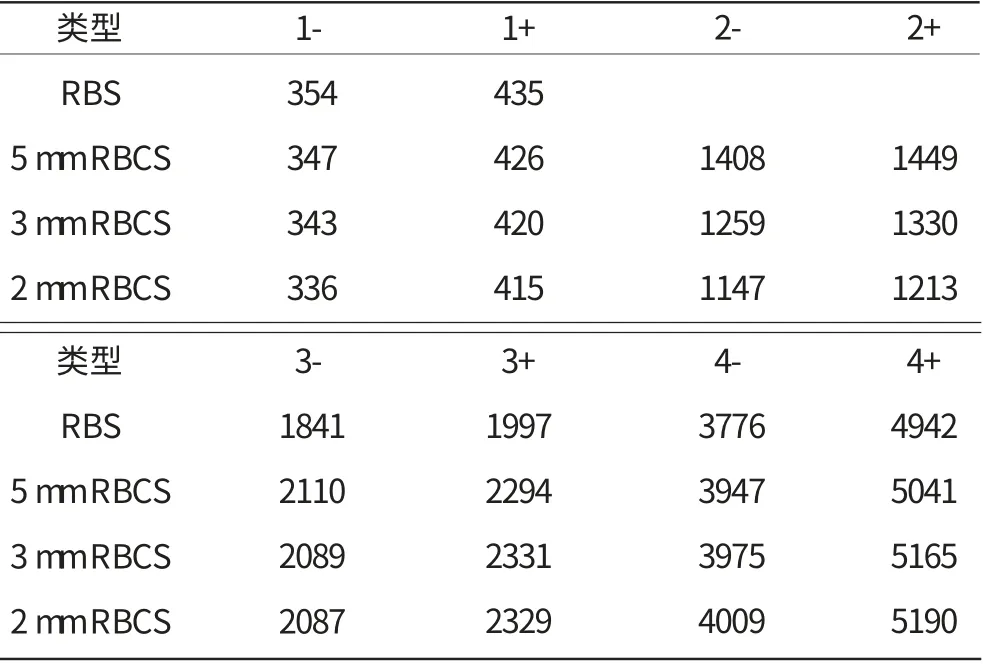
表4 轉子-支承系統(RBS)與轉子-支承-機匣系統(RBCS)前4階臨界轉速 rad/s

圖14 轉子-支承-機匣系統第1階振型

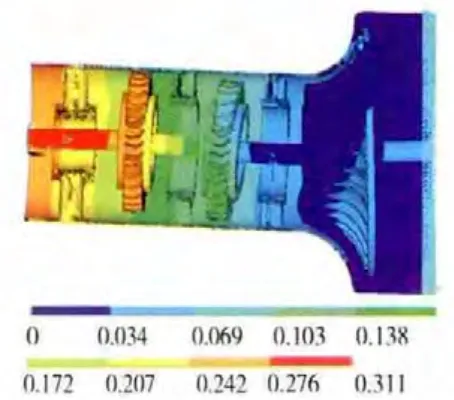
圖15 轉子-支承-機匣系統第2階振型

圖16 轉子-支承-機匣系統第3階振型

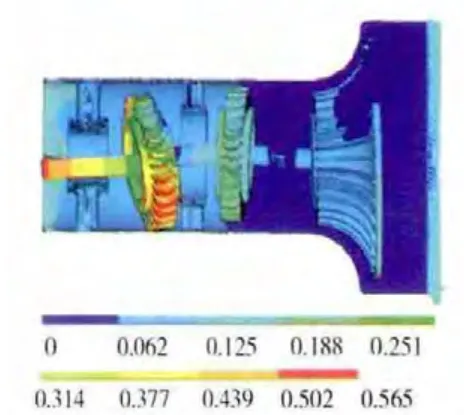
圖17 轉子-支承-機匣系統第4階振型

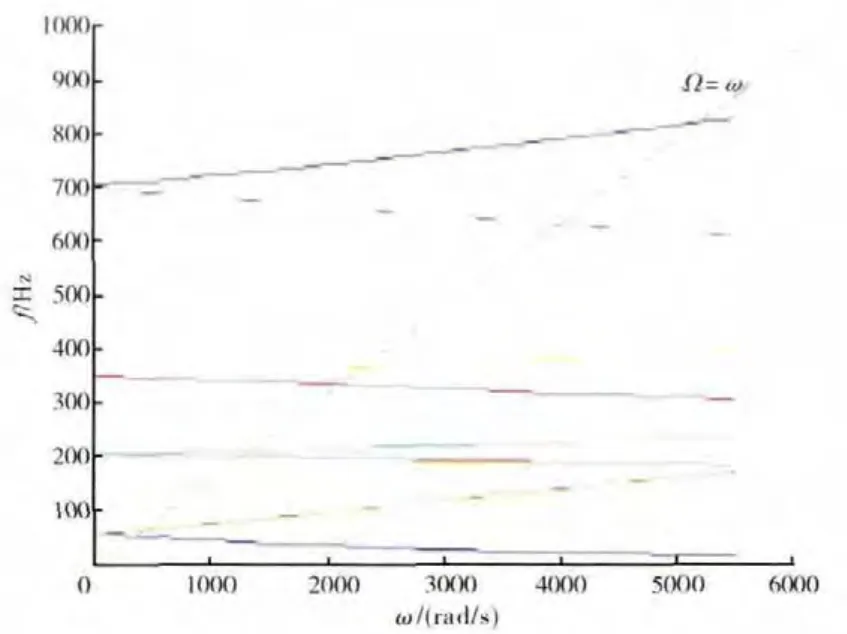
圖18 3mmRBCScampbell

從表4中可見，各組合壓氣機系統的第2階臨界轉速和機匣第1階固有頻率均隨機匣厚度的減小而降低，且其臨界轉速也比對應的機匣第1階固有頻率有所下降。

5 不平衡響應分析

不平衡響應分析是旋轉機械系統動力特性分析的重要部分，可以預測轉子系統在某些工況下的振動情況，還可確定轉子在計及阻尼影響時的臨界轉速[15]。本文利用ANSYS軟件對機匣厚度為3mm的組合壓氣機模型進行不平衡響應分析，從而驗證計算所得臨界轉速正確與否。在第1級軸流式輪盤施加5g·mm的不平衡量，阻尼比為0.01，在轉子轉速為600~60000r/min范圍內，計算位于靜子部件上的前、后支承點處的振動響應，在對數變換下，其響應值隨轉速變化的曲線如圖19所示。

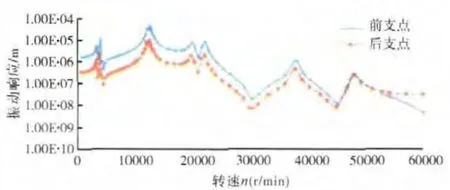
圖19 機匣前、后支點振動響應隨轉速變化曲線

從圖19中可見，其響應值在8個轉速值處達到峰值，將該峰值轉速與上文計算所得臨界轉速進行對比，其結果見表5。

從表5中可見，機匣前、后支點的振動響應峰值轉速與計算所得系統臨界轉速誤差很小，驗證了計算所得臨界轉速值的正確性。

6 結論

（1）組合壓氣機轉子-支承-機匣系統的各階臨界轉速低于對應的轉子-支承系統的臨界轉速，且出現了以機匣彎曲振動為主振型的臨界轉速。

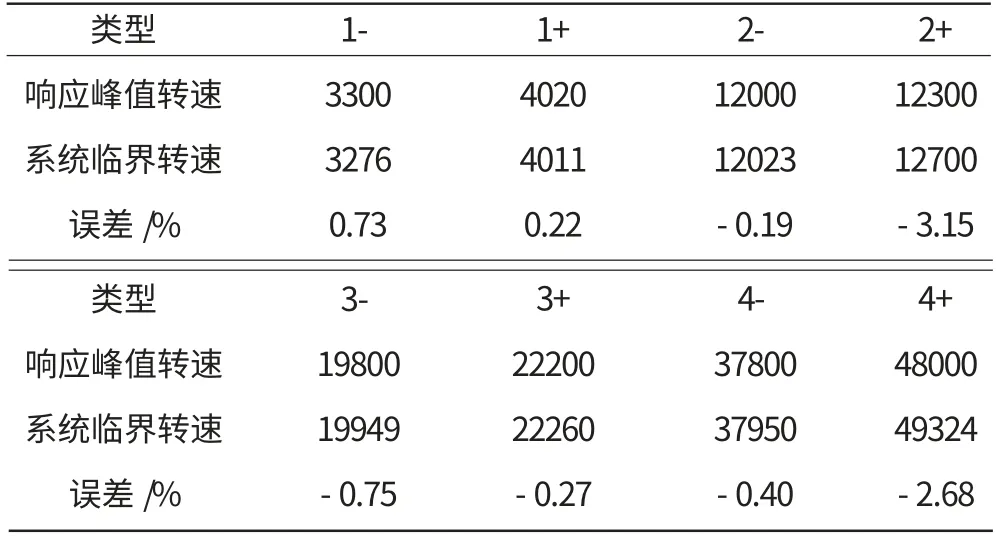
表5 支點振動響應峰值轉速與系統臨界轉速對比 r/min

（2）隨著機匣厚度的減小，組合壓氣機機匣部件的固有頻率隨之下降，而其轉子-支承-機匣系統的第1、2階臨界轉速也隨之下降，第4階臨界轉速則隨之升高。

（3）組合壓氣機機匣前后支點的振動響應峰值轉速與系統臨界轉速值相吻合，驗證了臨界轉速的正確性。

[1]Prohl M A.A general method of calculating critical speeds of flexible rotors[J].ASME,1945（67）：142-146.

[2]Gunter E J.Unbalance response of a two spool gas turbine engine with squeeze film bearings[R].ASME 81-GT-219.

[3]Gunter E J.Design of nonlinear squeeze-film dampers for aircraft engines[J].Journal of Lubrication Technology，1999（1）：57-64.

[4]Kazao Y，Gunter E J.Dynamics of multi-spool gas turbines using the matrix transfer method applications[J].International Journal of Turbo and Jet Engines,1990（6）：143-152.

[5]趙明，魏德明，任平珍，等.模態綜合法計算雙轉子臨界轉速研究[J].燃氣渦輪試驗與研究，2003，16（3）：38-41.ZHAO Ming，WEI Deming，REN Pingzhen，et al.Study of twin-rotor critical speed by mode synthesis[J].Gas Turbine Experiment and Research，2003，16（3）：38-41.(in Chinese)

[6]張謙，曹磊.基于ANSYS的臨界轉速計算[J].振動工程學報，2004，17（Sl）：234-237.ZHANG Qian，CAO Lei.Critical speed analysis based on ANSYS[J].Journal of Vibration Engineering，2004，17（S1）：234-237.(in Chinese)

[7]Chiang H W,Hsu C N,Tu S H.Rotor-bearing analysis for turbomachinery single and dual rotor systems[J].Journal of Propulsion and Power，2004，20（6）：1096-1104.

[8]Wei H,Chiang D，Hsu CN.Turbomachinery dual rotor bearing system analysis[R].ASME 2002-GT-30315.

[9]陳萌，洪杰，朱彬，等.基于實體單元的轉子動力特性計算方法[J].北京航空航天大學學報，2007，33（1）：10-13.CHEN Meng，HONG Jie，ZHU Bin，et al.Rotor dynamic anal ysis based on solid element[J].Journal of Beihang University，2007，33（1）：10-13.(in Chinese)

[10]陳萌，馬艷紅，劉書國，等.航空發動機整機有限元模型轉子動力學分析[J].北京航空航天大學學報，2007，33（9）：1013-1016.CHEN Meng，MA Yanhong，LIU Shuguo，et al.Rotor dynamic analysis of whole aero engine models based on finite flement method[J].Journal of Beihang University，2007，33（9）：1013-1016.(in Chinese)

[11]洪杰，王華，肖大為，等.轉子支承動剛度對轉子動力特性的影響分析[J].航空發動機，2008，34（1）：23-27.HONG Jie，WANG Hua，XIAO Dawei，et al.Effects of dynamic stiffness of rotor bearing on rotor dynamic characteristics[J].Aeroengine，2008，34（1）：23-27.(in Chinese)

[12]Chen G.A new rotor ball bearing stator coupling dynamic model for whole aeroengine vibration[J].Journal of Vibration and Acoustics，2009，131（6）：061009-1-061009-9.

[13]陳果.雙轉子航空發動機整機振動建模與分析[J].振動工程學報，2011，24（6）：619-632.CHEN Guo.Vibration modeling and analysis for dual rotor aeroengine[J].Journal of Vibration Engineering，2011，24（6）：619-632.(in Chinese)

[14]鐘一鄂，何衍宗，王正.轉子動力學[M].北京：清華大學出版社，1987：143-194.ZONG Yi’e,HE Yanzong,WANG Zheng.Rotor dynamics[M].Beijing:Tsinghua University Press,1987,143-194.(in Chinese)

[15]顧家柳，丁奎元，劉啟洲，等.轉子動力學[M].北京：國防工業出版社，1985：59-94.GU Jialiu,DING Kuiyuan,LIU Qizhou,et al.Rotor dynamics[M].Beijing:National Defence Industry Press,1985:59-94.(in Chinese)