高考中的傳送帶問(wèn)題
馬志偉
(衡水中學(xué) 河北 衡水 053000)
傳送帶模型是高中物理中比較成熟的模型,在高中物理中占有十分重要的地位,而高考中又經(jīng)常涉及到此類(lèi)問(wèn)題.為此,筆者對(duì)傳送帶問(wèn)題的求解方法進(jìn)行了總結(jié),現(xiàn)歸納如下.
1 水平傳送帶
【例1】水平傳送裝置如圖1所示,在載物臺(tái)左端給物塊一個(gè)初速度v0,當(dāng)它通過(guò)如圖示方向轉(zhuǎn)動(dòng)的傳送帶所用時(shí)間為t1.當(dāng)皮帶輪改為與圖示相反的方向傳送時(shí),通過(guò)傳送帶的時(shí)間為t2.當(dāng)皮帶輪不轉(zhuǎn)動(dòng)時(shí),通過(guò)傳送帶的時(shí)間為t3,則
A.t1一定小于t2B.t2>t3>t1
C.可能有t3=t2=t1D.一定有t1=t2<t3
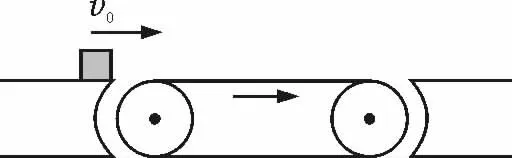
圖1
解析:傳送帶不動(dòng)時(shí),物塊做勻減速直線運(yùn)動(dòng),傳到右端時(shí)間為t3,若傳送帶順時(shí)針轉(zhuǎn),但物塊速度大于帶速時(shí),物塊仍可能一直減速,則t1=t3,同理傳送帶逆時(shí)轉(zhuǎn),物塊傳到右端速度未減為零時(shí)t2=t3,故應(yīng)選C.
12成.兩輪軸心相距L=8.0m,輪與傳送帶不打滑.現(xiàn)用此裝置運(yùn)送一袋面粉,已知面粉袋與傳送帶間的動(dòng)摩擦因數(shù)為μ=0.4.面粉可不斷地從袋中滲出.(g=10m/s2)
(1)當(dāng)傳送帶以v0=4.0m/s的速度勻速運(yùn)動(dòng)時(shí),將這袋面粉由左端O2正上方的A點(diǎn)輕放在傳送帶上后,這袋面粉由A端運(yùn)送到O1正上方的B端所用時(shí)間為多少?
(2)要想盡快將這袋面粉由A端送到B端(設(shè)袋的初速度仍為零),傳送帶的速度至少應(yīng)為多大?
(3)由于面粉的滲漏,在運(yùn)送這袋面粉的過(guò)程中會(huì)在深色傳送帶上留下白色的面粉的痕跡.這袋面粉在傳送帶上留下的痕跡最長(zhǎng)能有多長(zhǎng)(設(shè)袋的初速度仍為零)?此時(shí)傳送帶的速度至少應(yīng)為多大?
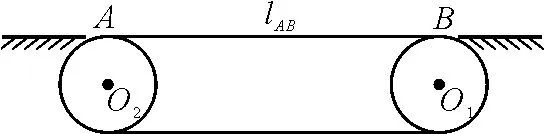
圖2
解析:(1)設(shè)面粉袋的質(zhì)量為m,其在與傳送帶產(chǎn)生相對(duì)滑動(dòng)的過(guò)程中所受的摩擦力f=μmg.
故而其加速度為
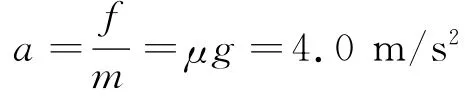
若傳送速帶的速度v帶=4.0m/s,則面粉袋加速運(yùn)動(dòng)的時(shí)間為
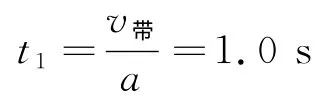
在t1時(shí)間內(nèi)的位移為
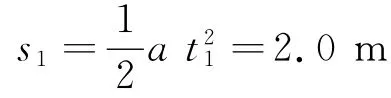
其后以v=4.0m/s的速度做勻速運(yùn)動(dòng)

解得t2=1.5s,運(yùn)動(dòng)的總時(shí)間為
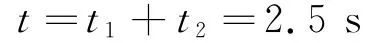
(2)要想時(shí)間最短,m 應(yīng)一直向B端做加速運(yùn)動(dòng),由
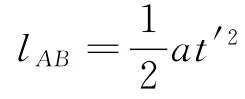
可得
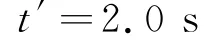
此時(shí)傳送帶的運(yùn)轉(zhuǎn)速度為
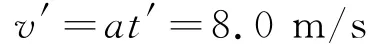
(3)傳送帶的速度越大,“痕跡”越長(zhǎng).當(dāng)面粉的痕跡布滿整條傳送帶時(shí),痕跡達(dá)到最長(zhǎng).即痕跡長(zhǎng)為
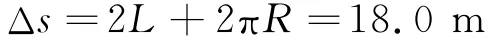
在面粉袋由A端運(yùn)動(dòng)到B端的時(shí)間內(nèi),傳送帶運(yùn)轉(zhuǎn)的距離
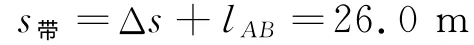
又由第(2)問(wèn)中已知
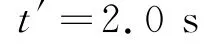
此時(shí)傳送帶的運(yùn)轉(zhuǎn)速度為
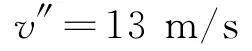
2 傾斜傳送帶
【例3】如圖3所示,物塊M 在靜止的傳送帶上以速度v勻速下滑時(shí),傳送帶突然啟動(dòng),方向如圖箭頭所示,若傳送帶的速度大小也為v,則傳送帶啟動(dòng)后
A.M 靜止在傳送帶上
B.M 可能沿斜面向上運(yùn)動(dòng)
C.M 受到的摩擦力不變
D.M 下滑的速度不變
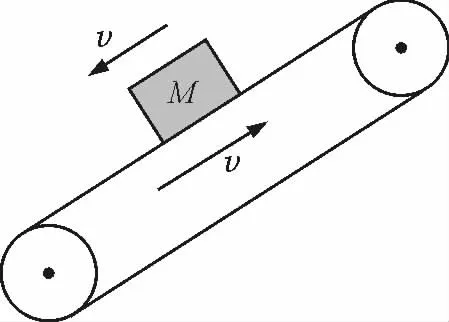
圖3
解析:物塊M 在靜止的傳送帶上勻速下滑,則Ff=mgsinθ.當(dāng)傳送帶突然啟動(dòng)向上運(yùn)動(dòng)時(shí)物塊M 受到方向沿傳送帶向上的滑動(dòng)摩擦力、重力和支持力.由前面條件可知著3個(gè)力的合力為零,所以物塊M的運(yùn)動(dòng)狀態(tài)不變,繼續(xù)以速度v勻速下滑.答案為選項(xiàng)C,D.
【例4】如圖4所示,傳送帶與地面成夾角θ=30°,以10m/s的速度逆時(shí)針轉(zhuǎn)動(dòng),在傳送帶上端輕輕地放一個(gè)質(zhì)量m=0.5kg的物體,它與傳送帶間的動(dòng)摩擦因數(shù)μ=0.6,已知傳送帶從A到B的長(zhǎng)度L=16m,則物體從A到B需要的時(shí)間為多少?(g=9.8m/s2)
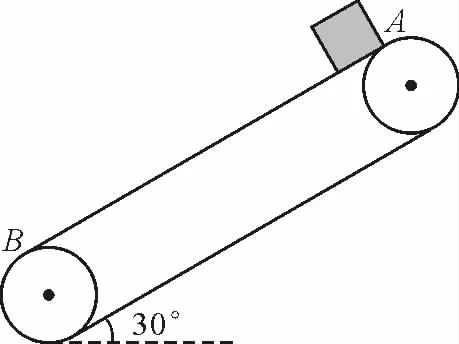
圖4
解析:該題目的關(guān)鍵就是要分析好各階段物體所受摩擦力的大小和方向,μ>tanθ=,第二階段物體將和傳送帶相對(duì)靜止一起向下勻速運(yùn)動(dòng).
物體放上傳送帶以后,開(kāi)始一段時(shí)間,其運(yùn)動(dòng)加速度
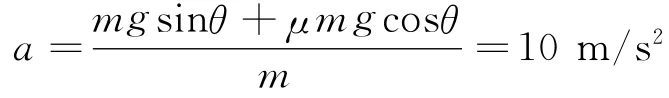
這樣的加速度只能維持到物體的速度達(dá)到10 m/s為止,其對(duì)應(yīng)的時(shí)間和位移分別為
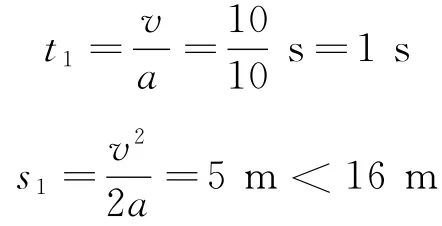
以后物體受到的摩擦力變?yōu)檠貍魉蛶蛏希浼铀俣却笮榱悖ㄒ驗(yàn)閙gsinθ<μmgcosθ).
設(shè)物體完成剩余的位移s2所用的時(shí)間為t2,則
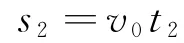
解得
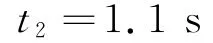
所以
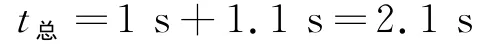
3 涉及能量的問(wèn)題
求傳送帶對(duì)物體所做的功、物體和傳送帶由于相對(duì)滑動(dòng)而產(chǎn)生的熱量、因放上物體而使電動(dòng)機(jī)多消耗的電能等,常依據(jù)功能關(guān)系或能量守恒定律求解.
【例5】如圖5所示,繃緊的傳送帶與水平面的夾角θ=30°,皮帶在電動(dòng)機(jī)的帶動(dòng)下,始終保持v0=2m/s的速率運(yùn)行.將一質(zhì)量m=10kg的工件(可看為質(zhì)點(diǎn))輕輕放在皮帶的底端A點(diǎn),工件能被傳送到頂端B點(diǎn).已知工件與皮帶間的動(dòng)摩擦因數(shù)μ,A點(diǎn)與B點(diǎn)的高度差h=2m,取g=10m/s2.
求:因運(yùn)送此工件,電動(dòng)機(jī)需多消耗的電能E.
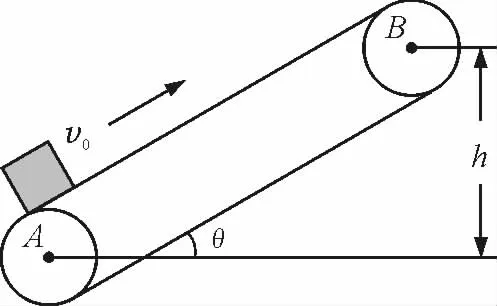
圖5
解析:
工件運(yùn)動(dòng)的加速度為
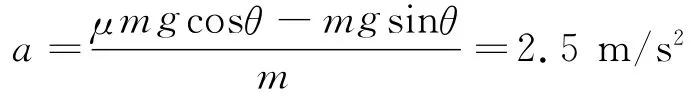
工件上升長(zhǎng)度
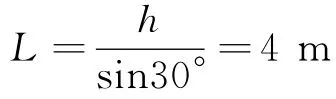
工件能加速上升的總長(zhǎng)度為
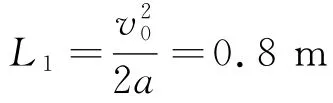
加速總時(shí)間為
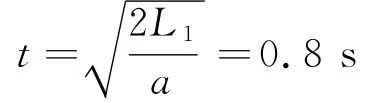
加速時(shí)間為傳送帶移動(dòng)距離為
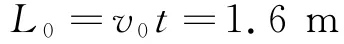
工件摩擦產(chǎn)生的熱量為
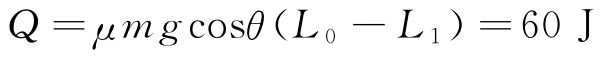
電動(dòng)機(jī)額外做的功為
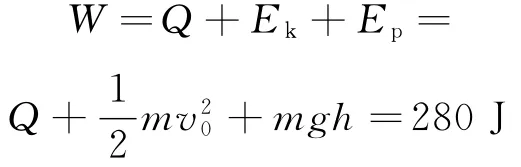
【例6】如圖6所示,以A,B和C,D為斷點(diǎn)的兩半圓形光滑軌道固定于豎直平面內(nèi),一滑板靜止在光滑的地面上,左端緊靠B點(diǎn),上表面所在平面與兩半圓分別相切于B,C兩點(diǎn),一物塊(視為質(zhì)點(diǎn))被輕放在水平勻速運(yùn)動(dòng)的傳送帶上E點(diǎn),運(yùn)動(dòng)到A點(diǎn)時(shí)剛好與傳送帶速度相同,然后經(jīng)A點(diǎn)沿半圓軌道滑下,再經(jīng)B點(diǎn)滑上滑板,滑板運(yùn)動(dòng)到C點(diǎn)時(shí)被牢固粘連.物塊可視為質(zhì)點(diǎn),質(zhì)量為m,滑板質(zhì)量為M=2m,兩半圓半徑均為R,板長(zhǎng)l=6.5R,板右端到C點(diǎn)的距離L在R<L<5R范圍內(nèi)取值,E點(diǎn)距A點(diǎn)的距離s=5R,物塊與傳送帶、物塊與滑板間的動(dòng)摩擦因數(shù)均為μ=0.5,重力加速度g已知.
(1)求物塊滑到B點(diǎn)的速度大小;
(2)求物塊滑到B點(diǎn)時(shí)所受半圓軌道的支持力的大小;
(3)物塊在滑板上滑動(dòng)過(guò)程中,當(dāng)物塊與滑板達(dá)到共同速度時(shí),測(cè)得它們的共同速度為v=試討論物塊從滑上滑板到離開(kāi)右端的過(guò)程中,克服摩擦力做的功Wf與L的關(guān)系;并判斷物塊能否滑到CD軌道的中點(diǎn).

圖6
解析:(1)設(shè)物塊滑到B點(diǎn)的速度大小為vB,對(duì)物體從E到B過(guò)程,根據(jù)動(dòng)能定理,得
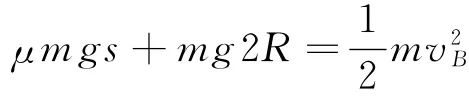
解得
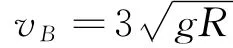
(2)物塊在B點(diǎn)時(shí),根據(jù)牛頓第二定律,得
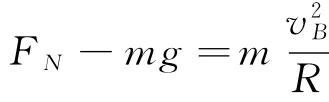
解得
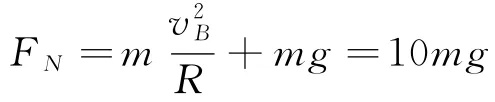
(3)物塊從B滑上滑板后開(kāi)始做勻速運(yùn)動(dòng),此時(shí)滑板開(kāi)始做勻速直線運(yùn)動(dòng),當(dāng)物塊與滑板達(dá)共同速度時(shí),二者開(kāi)始做勻速運(yùn)動(dòng).由題意知它們的共同速度為
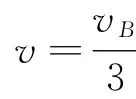
此過(guò)程,對(duì)物塊根據(jù)動(dòng)能定理,得
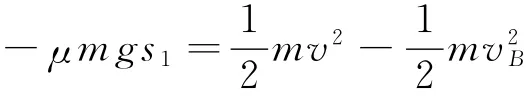
解得 s1=8R
此過(guò)程,對(duì)滑板根據(jù)動(dòng)能定理,得
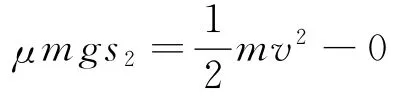
解得
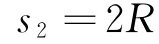
由此可知物塊在滑板上滑過(guò)s1-s2=6R時(shí),二者就具有共同速度了.因?yàn)?R<6.5R,所以物塊并沒(méi)有從滑板上滑下去.
討論:
(1)當(dāng)R<L<2R時(shí),物塊在滑板上一直做勻減速運(yùn)動(dòng)至右端,運(yùn)動(dòng)的位移為6.5R+L,克服摩擦力做的功
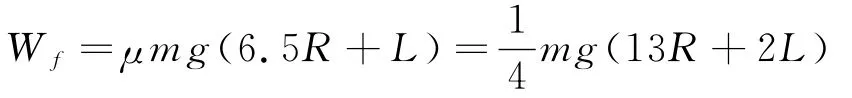
設(shè)滑上C點(diǎn)的速度為vC,對(duì)物塊根據(jù)動(dòng)能定理得
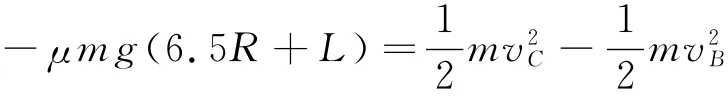
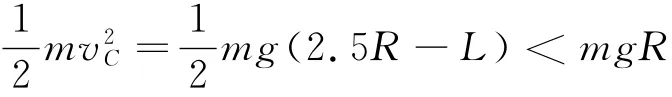
解得所以物塊不可能滑到CD軌道的中點(diǎn).
(2)當(dāng)2R≤L<5R時(shí),物塊的運(yùn)動(dòng)的勻減速運(yùn)動(dòng)8R,勻速運(yùn)動(dòng)L-2R,再勻減速運(yùn)動(dòng)0.5R,克服摩擦力做的功
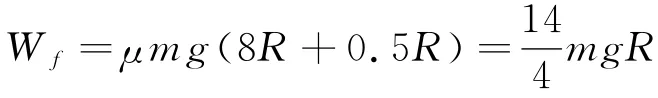
解得
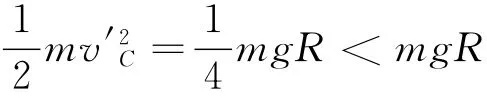
所以物塊不能滑到CD軌道的中點(diǎn).
在求解傳送帶問(wèn)題時(shí),一定要看清題目給定的條件,具體問(wèn)題具體分析,選擇恰當(dāng)?shù)姆椒ㄟM(jìn)行解題,千萬(wàn)不要盲目地亂套公式.

