無刷直流電機網絡伺服控制技術研究
祁樹勝,祁 特
(1.西安航空學院 電氣學院,陜西 西安 710077;2.天津大學 材料科學與工程學院,天津 300072)
1 簡介
近些年來,電機網絡控制已成為運動控制技術領域的研究熱點之一。網絡的應用為系統帶來了諸多的優勢,同時也給系統的控制帶來了一些難題,如傳輸延時,數據包丟失等。這些問題不但會影響系統的動態特性,還有可能使系統變得不穩定。因此,網絡的引入還使系統的分析變得更加復雜,系統的控制也變得困難。
本文提出了一種無刷直流電機網絡伺服控制系統的設計方案。考慮了網絡系統前向及反饋通道均存在延時的情況,網絡伺服控制器采用基于模糊自適應調節的廣義預測控制算法。在假設網絡延時有界的前提下,考慮了雙向延時對系統控制特性的影響,采用預測控制算法計算控制律以改善系統的魯棒性,以模糊自適應調節算法來克服系統參數不確定對系統控制特性的影響。
2 系統分析
系統結構如圖1所示。系統包括:網絡控制器,網絡延時補償器,電機本體,傳感器和執行器。傳感器和執行器為時間驅動。控制器為事件-時間驅動。執行器端設置延時補償器以補償前向通道延時。反饋通道延時補償由網絡控制器完成。
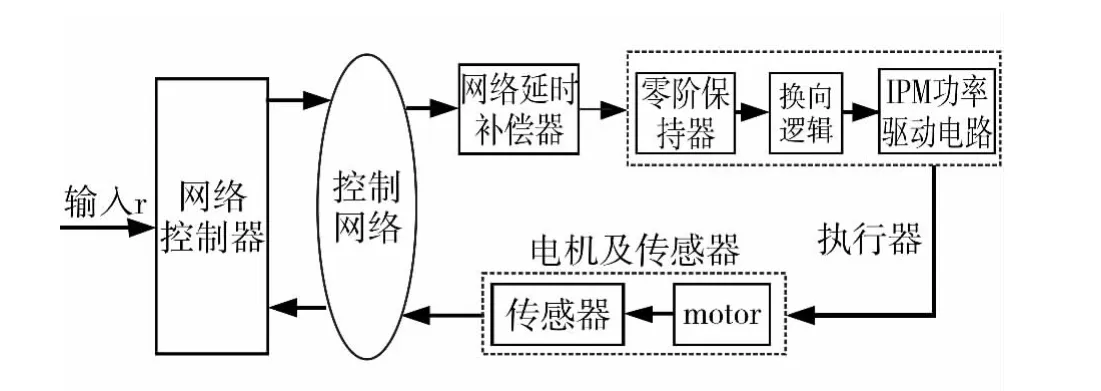
圖1 系統結構圖
2.1 電機模型
無刷直流電動機工作在兩相導通星形三相6狀態方式下,電磁轉矩方程為:
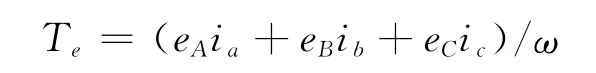
式中:Te為電磁轉矩,N·m;ω為電動機轉子機械角速度,rad/s。電機機械運動方程:
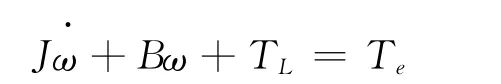
式中:TL為負載轉矩,Nom;J為電機轉動慣量,kg/m2。
由于無刷直流電動機工作在兩相導通星形三相6狀態方式下,則有:
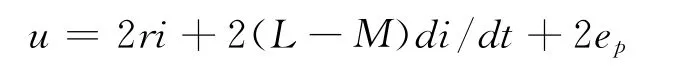
式中:u為導通兩相的支路電壓,V;i為導通兩相的支路電流,A;ep為導通相的相反電動勢,V。
由電磁轉矩方程可得:
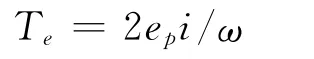
由于反電動勢波形的平頂寬度為120°電角度的梯形波,則有:ep=Keω
式中Ke為電動勢系數,V/(rad/s)。
將以上各式進行拉氏變換可得:
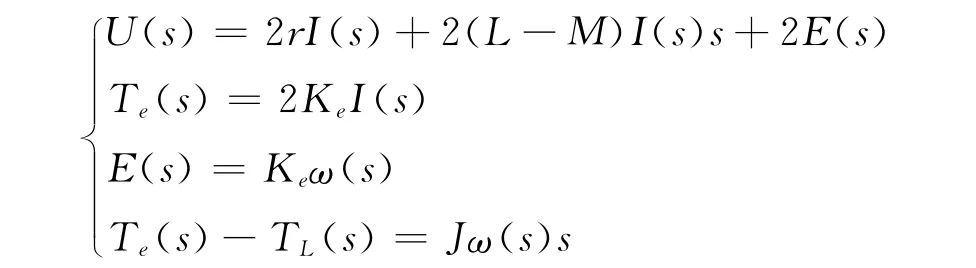
可把負載轉矩TL看成一種干擾,考慮空載情況,可得:
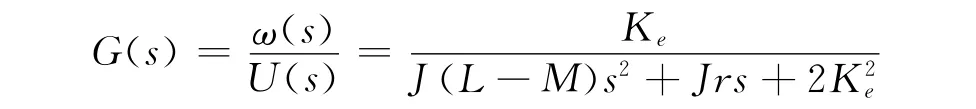
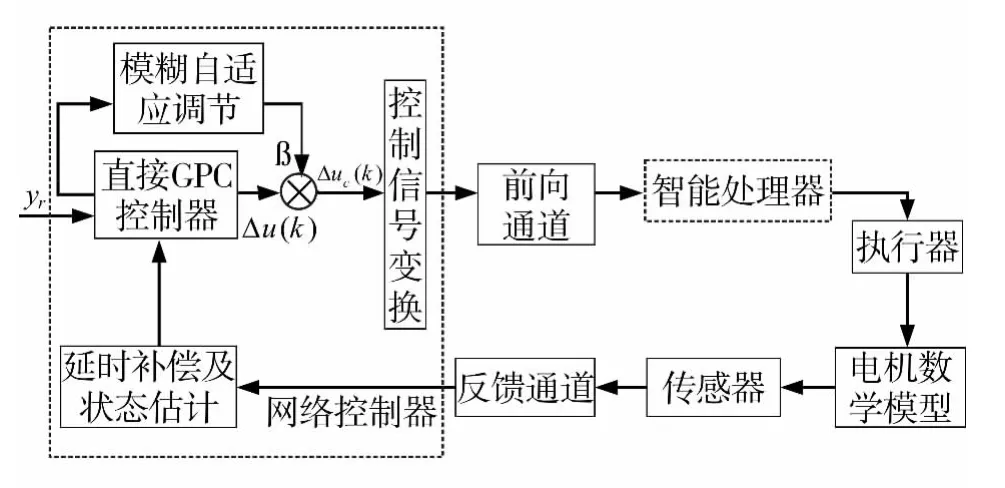
圖2 控制系統原理圖
2.2 基于模糊自適應調節的廣義預測控制器的設計
網絡控制系統原理圖如圖2所示。圖中采用智能處理器作為執行器的延時補償器。網絡控制器由GPC控制器、延時補償及狀態估計、模糊自適應調節器及控制信號變換器組成。被控對象數學模型可表示為:

根據Diophantine方程,可以得到被控對象前向預測方程:
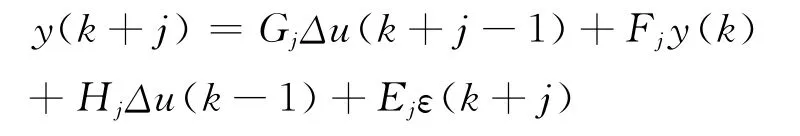
定義:
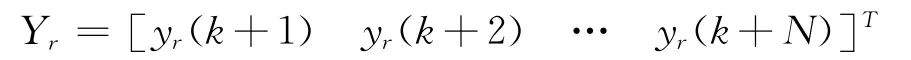
則性能指標函數可表示為:
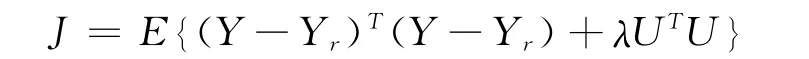
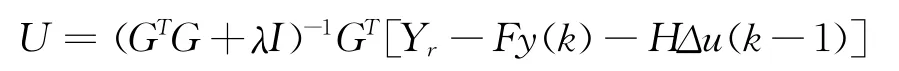
取(GTG+λI)-1GT的第一行記為:
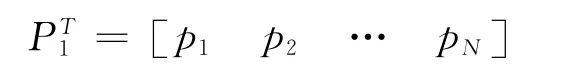
根據滾動優化和反饋校正的原理,控制律增量可表示如下:
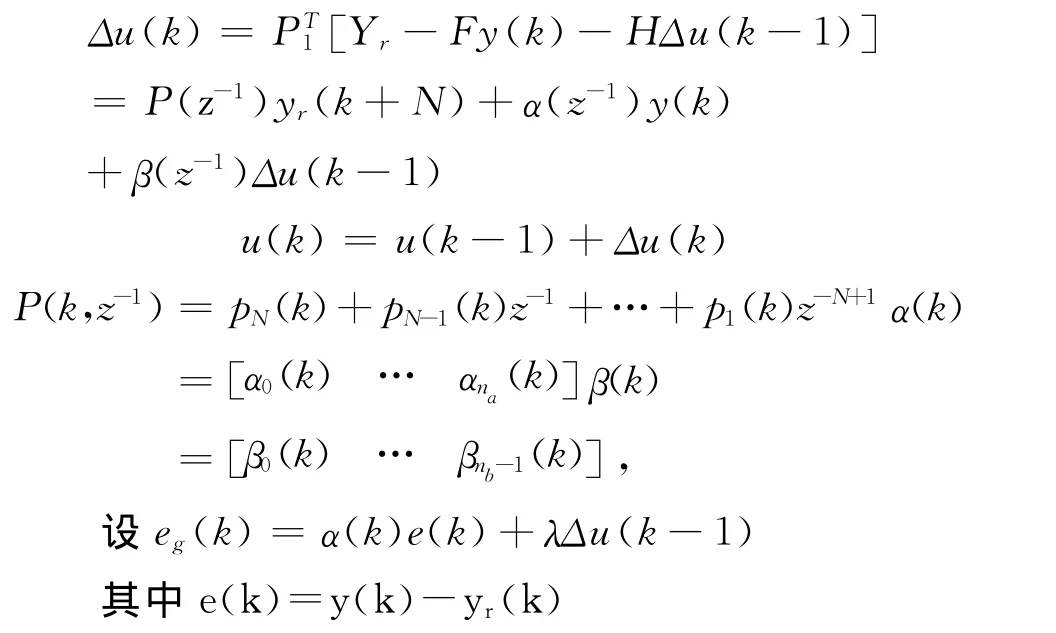
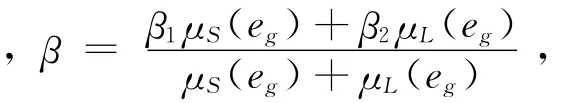
網絡控制器的輸出為:
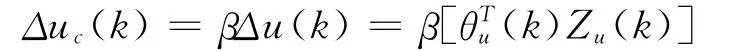
采用如下模糊控制規則:

βi是和β對應的跟隨參數,β1和β2的模糊自適應調節算法采用在線調整的方法。
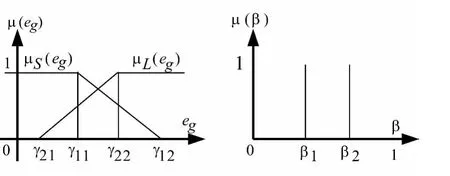
圖3 輸入eg,輸出β的隸屬度函數
隸屬度函數參數μS(eg),μL(eg)定義如下:
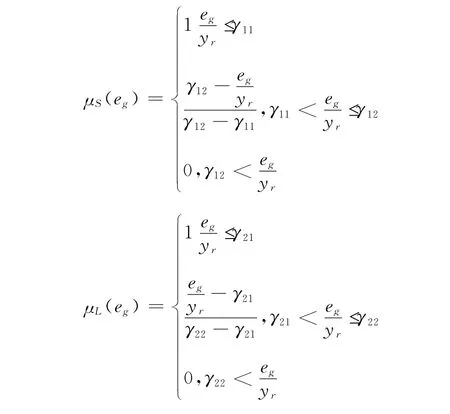
其中,yr為參考輸入,其中0<γ21<γ11<γ22<γ12<1,0<β1<β2<1.則瞬態性能指標J(k)定義為:
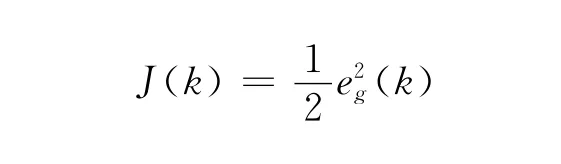
由最速下降法可有:
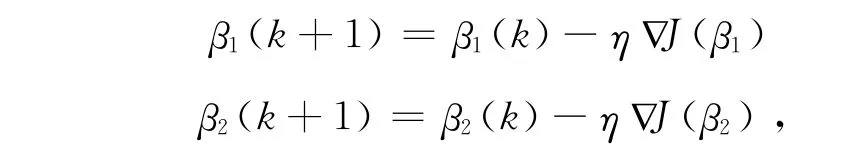
其中為下降速率,且:
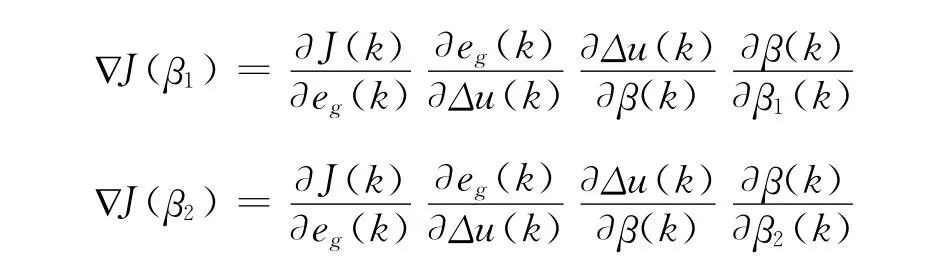
由于控制器選擇為直接GPC控制,則:綜合整理后,設
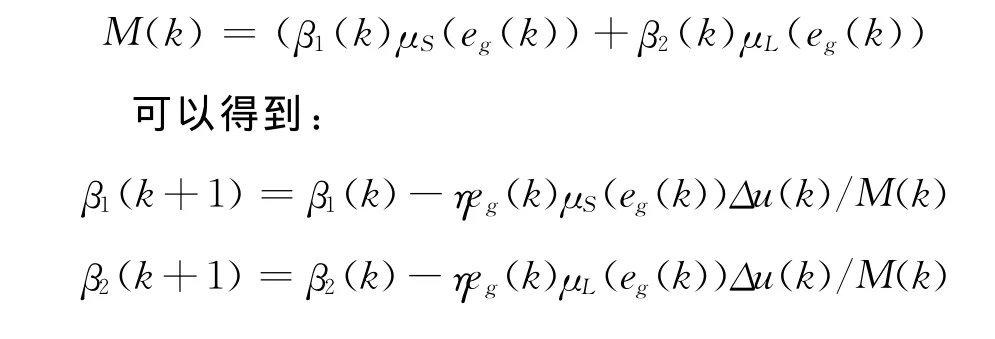
3 仿真實例
本文基于MATLAB2008/SIMULINK,建立無刷直流電機控制系統模型。電機參數設置為:定子相繞組電阻R=0.5Ω;定子相繞組自感L=0.04H;互感 M=-0.0055H;轉動慣量J=0.02kg·m2;阻尼系數B=0.0002N·m·s/rad;極對數P=2;每相反電動勢系數k=0.03;150V直流電源供電。
情況1:GPC本地控制。此時,控制環內無網絡。GPC控制的仿真結果如圖4所示。
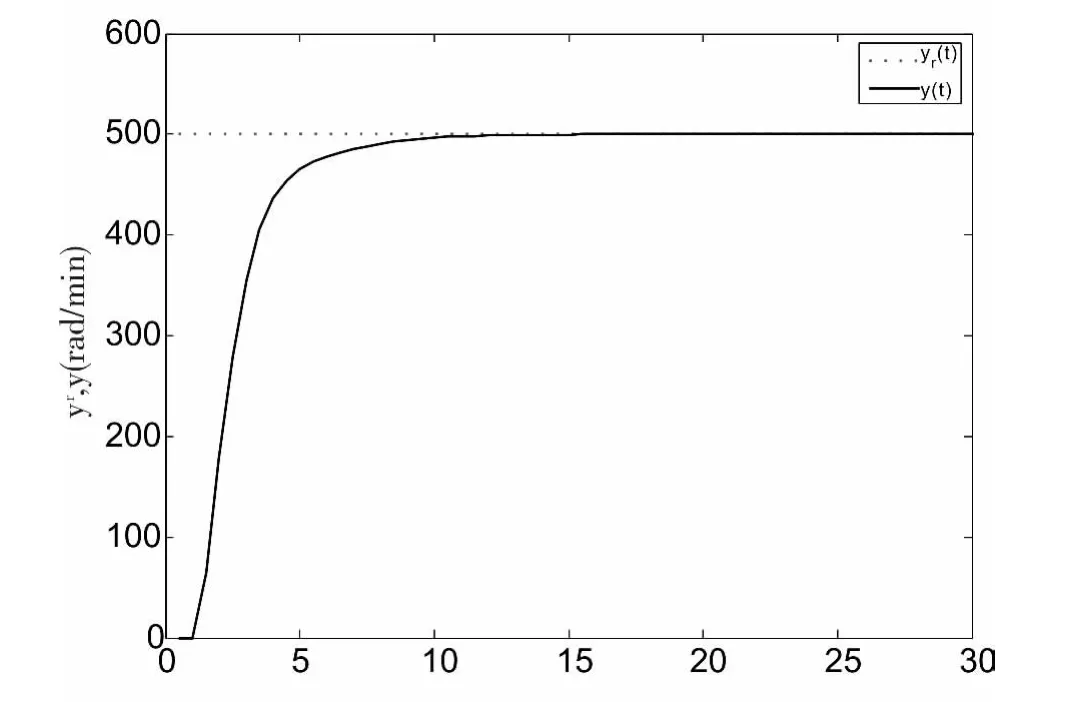
圖4 本地控制波形
情況2:無模糊自適應調節的GPC網絡控制
GPC控制可以補償網絡延時。網絡總延時不超過3個采樣周期。仿真結果如圖5所示。
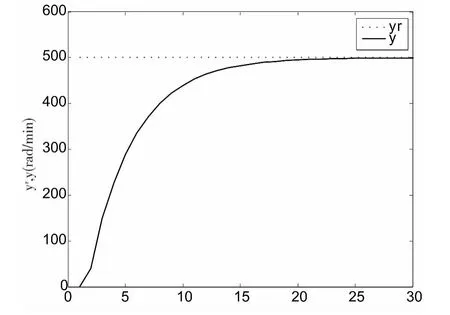
圖5 GPC控制波形
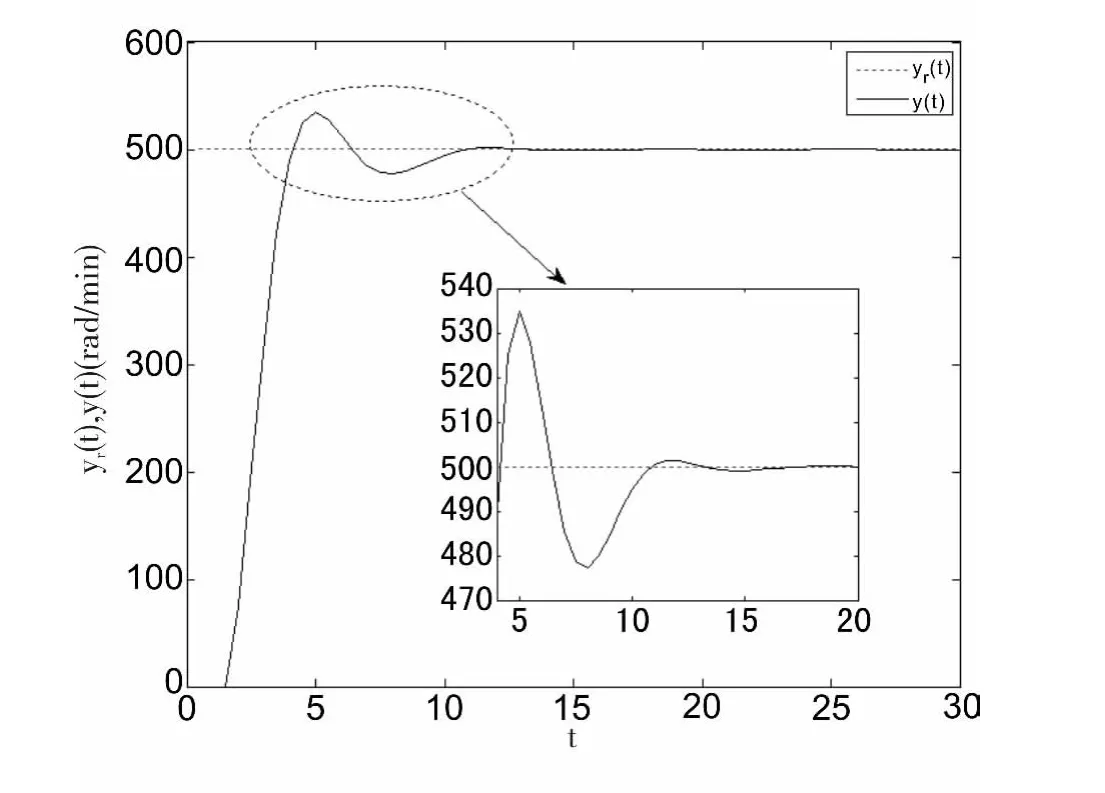
圖6 具有模糊自適應調節的GPC控制
情況3:具有模糊自適應調節的GPC控制。此時網絡總延時不超過3個采樣周期。速度響應如圖6所示。相比常規的GPC控制,調節時間減小,經過一次振蕩,系統快速進入穩態。仿真結果表明了該控制系統良好的快速性。
4 結語
本文提出針對具有雙向有界延時,即具有前向及反饋通道延時的直流電機網絡控制設計方案。設計了基于模糊自適應調節的廣義預測控制算法的網絡控制器。采用預測控制算法計算控制律以減小網絡延時對系統控制特性的影響,同時能改善系統的魯棒性。模糊自適應調節用于進一步提高系統的快速性。仿真結果證明了該法的有效性。
[1]Y.Xia,G.-P.Liu,M.Fu,et al.Predictive control of Networked systems with random network delays and data dropout[J].IET Theory and Application,2009,11(3):1476-1486.
[2]LI H,CHOW M,SUN Z.Optimal stabilizing gain selection for networked control systems with time delays and packet losses[J].IEEE Transactions on Control Systems Technology,2009,17(5):154-162.
[3]N.B.Almutairi,Mo-Yuen Chow.Adaptive fuzzy modulation(AFM)for IP networked PI control systems-part Ι:Partial adaptation [J].IECON,2002(6):3152-3157.
[4]Liu G.p,Mu J.Design and stability analysis of networked control systems with random communication time delay using the modified MPC [J].Int.J.Control,2006,79(4):288-297.
[5]G.P.Liu,D.Rees,S.C.Chai,et al.Simulation and implementation of networked predictive control systems[J]Meas.Control,2005,38(1):17-21.

