復合射孔槍爆壓數值分析與動態塑性設計準則

霍一飛，舒淑寧，劉蔭忠，田 毅

（1.西北工業大學 航空學院，陜西 西安 710072；2.西安通源石油公司，陜西 西安 710065）

1 引言

復合射孔的結構設計離不開工況載荷，也離不開設計準則。否則該設計只是經驗之談，無法成為科學技術加以傳承。在復合射孔過程中，爆燃壓力除了與炸藥本身所具有的化學能相關外，火藥的裝藥量也對爆壓的峰值以及脈寬有密切的影響。長期以來工程結構設計一直沿用的強度理論，無論是靜強度還是動強度，都無法移植應用到射孔槍結構設計體系之中。這是因為射孔槍的結構設計既需要完成動態設計，又需要進行塑性設計分析。而目前現有設計理論體系中缺乏這類動態塑性設計準則，因此，這種動態塑性流變設計準則將會成為射孔槍結構設計的主要依據，建立該準則的意義就顯得十分重要。

爆燃壓力載荷實驗的研究文獻很多，主要探討載荷與裝藥關系的道理；這里應用LS－DYNA爆炸沖擊軟件分析復合射孔的爆燃載荷也是一種數值試驗方法，能夠大量節約復合射孔器的設計成本。LS－DYNA是美國為武器設計提供的分析軟件，它以Lagrange算法為主，兼有Euler算法；以顯式求解為主，兼有隱式求解功能；以結構分析為主，兼有熱分析、流體－結構耦合功能；以非線性動力分析為主，兼有靜力分析功能。LS－DYNA還具有很廣泛的分析功能，可模擬許多二、三維結構的物理特性。射孔槍設計的文獻也不少，但是除了實驗摸索、驗證和說明之外，沒有任何設計準則可以直接應用在結構設計中。雖然射孔槍的行業標準已經完成，并且規定了射孔后槍身脹形量的標準，但是如何做到這一標準卻是一個不斷實踐和理論升華的過程，也是本文拋磚引玉的目的之一。

通過LS－DYNA軟件對不同裝藥量所產生的壓力進行了數值模擬，以得到不同裝藥量下復合射孔的載荷規律。通過現有的強度設計準則比較和分析，探索一種全新的動態塑性流變的設計方法，期望能夠真正用于的射孔槍結構設計之中。

2 理論基礎

2.1 火炸藥的狀態方程

爆轟產物狀態方程式炸藥爆轟C－J狀態之后的爆轟產物系統中各物理量（壓力、體積、溫度）之間的關系，JWL狀態方程能夠比較精確的滿足描述爆轟產物的膨脹驅動過程。從狀態方程中可以看到，炸藥爆炸產生的壓力除了與炸藥本身所含有的化學能有關之外，火炸藥所處環境的體積也是影響爆壓的原因之一。因此有理由推斷，火藥除了能夠提供與炸藥耦合時候的壓力外，其在炸藥爆炸時候擠占的體積也會增加炸藥爆炸產生的壓力。

JWL狀態方程：

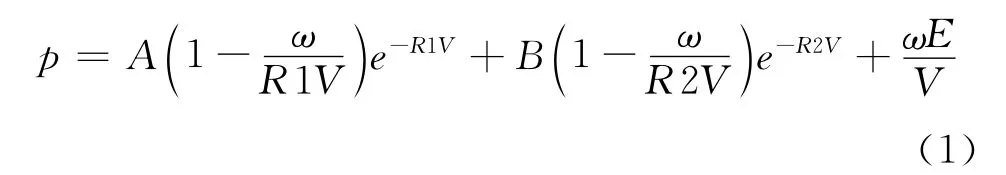
式中A，B，R1，R2，ω —材料常數；E—初始內能；V—相對體積。其中RDX炸藥的參數如下表1所示：

表1 RDX炸藥材料參數

2.2 材料動態本構模型

Johnson－Cook模型是一個基于經驗的材料本構關系式。此模型是大應變、高應變率和高溫狀態下的金屬本構方程。射孔槍32CrMo4材料采用Johnson－Cook熱粘性本構方程：

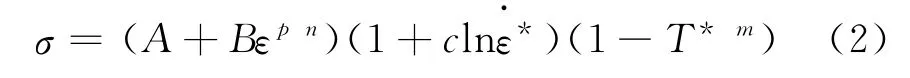
式中εp—等效塑性應變；等效塑性應變率；T＊—相對溫度。

由試驗研究確定的射孔槍材料32CrMo4的五個參數如下表2所示。據此，得到32CrMo4動態塑性流變特性的Johnson－Cook材料本構模型，能夠用于LS－DYNA爆燃數值仿真中。

表2 射孔槍身材料動態本構方程的相關參數

3 數值模擬及結果分析

3.1 復合射孔爆壓數值分析

用LS－DYNA軟件進行建立有限元模型進行數值模擬。其中圖1為復合射孔的槍身內部幾何結構（a）以及網格剖分（b），采用軸對稱模型計算。對幾何模型進行單元剖分，單元類型為六面體網格。火藥單元、炸藥單元、藥形罩單元、射孔彈殼體單元、空氣單元用任意拉格朗日歐拉網格（ALE）劃分，射孔槍身單元用拉格朗日網格劃分。其中火藥單元、炸藥單元、藥形罩單元、射孔彈殼體單元與空氣單元共節點，空氣單元網格覆蓋射孔槍單元網格。

圖1 射孔槍槍身結構和網格剖分

如圖2所示射流密度云圖，射孔時槍內形成射流杵體，并且該射流穿透了射孔槍壁。

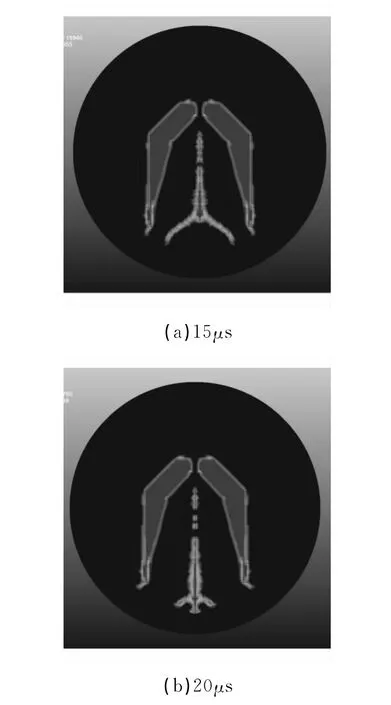
圖2 射流過程的射流密度云圖

為了研究復合射孔爆燃的空間體積對爆壓的影響，分別將火藥裝藥量調整為0g（火藥將不占體積）和15g計算，得到的對比曲線如圖3所示，該曲線為射流前端區域（非射流區）的壓力曲線。圖3中橫坐標單位是毫秒ms，縱坐標單位為GPa。

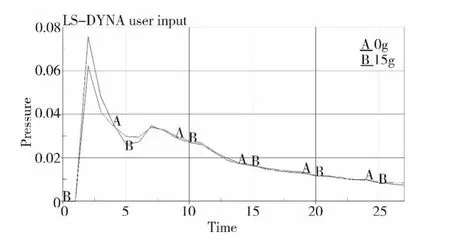
圖3 不同裝藥體積的射流前端區域爆壓曲線

由于火藥在射孔后3ms開始燃燒，從圖3可以看出在1ms到3ms之間出現壓力峰值，火藥裝藥量為15g的爆壓峰值大于0裝火藥的爆壓峰值，這說明復合射孔爆燃壓力峰值的影響因素不僅是炸藥以及火藥的化學能，還與復合射孔爆燃空間有關。下面分別計算了裝藥量為15g、25g、35g、40g、50g時槍身內壁與射流軸垂直區的壓力，計算結果得到如圖4所示的壓力曲線。圖中的橫坐標單位是毫秒ms，縱坐標單位為GPa。

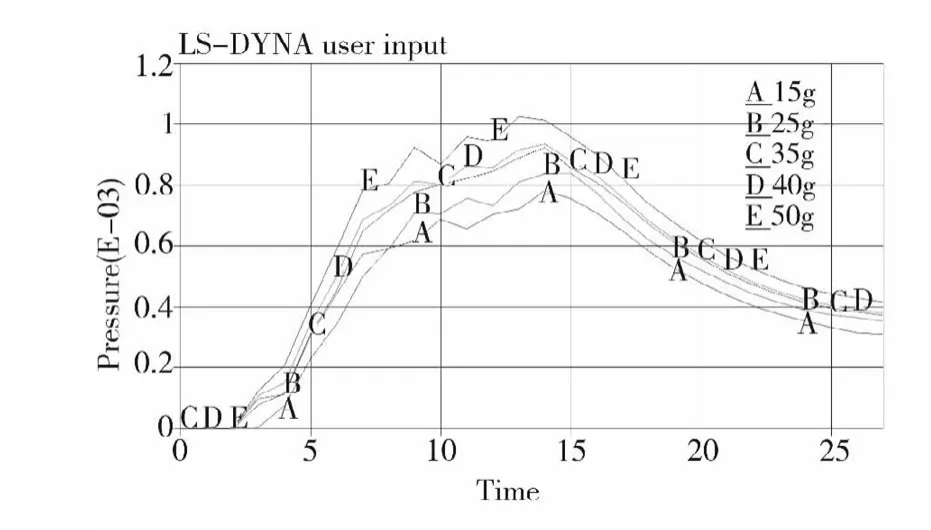
圖4 不同裝藥量壓力曲線

通過觀察圖4的曲線，火藥裝藥量除了對壓力峰值有影響（如圖5（a）所示的壓力峰值與裝藥量的遞增關系曲線）之外，對峰值區的脈寬也有影響，這是由于火藥燃燒是產生的高溫高壓對外膨脹做功，火藥越多，做功就越大，反映到P－T曲線上就是壓力峰值的脈寬與火藥裝藥量成正比，綜合考慮不同裝藥量下火藥的比沖能，將P－T曲線壓力對時間積分，如式（3），得到如圖5（b）所示的裝藥量的比沖能曲線。可以看到隨著火藥裝藥量與爆炸比沖成正比關系。

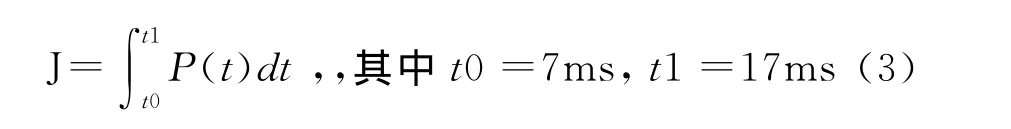
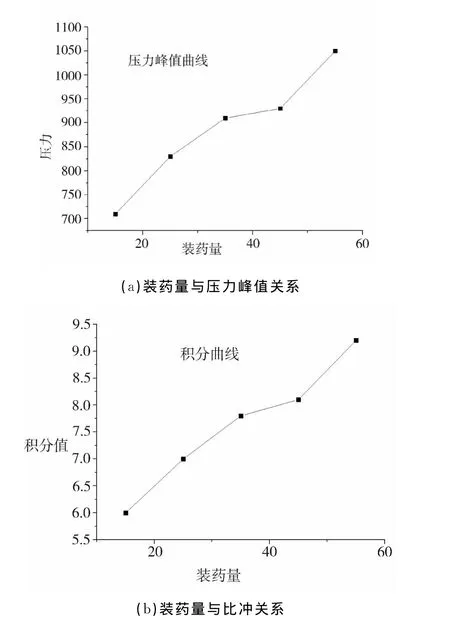
圖5 復合射孔裝藥量與壓力和比沖關系

3.2 塑性數值模擬及結果分析

根據射孔槍塑性變形以及復合射孔爆壓的數值模擬結果，射孔彈爆炸以及火藥燃燒產生的爆壓大于彈性極限載荷，小于極限塑性載荷，因此射孔槍必然存在塑性變形。隨著槍身內壓力的不斷增加，射孔槍從彈性變形狀態進入到塑性狀態，在槍身內壁形成塑性區，并且塑性區在卸載后出現了殘余變形。

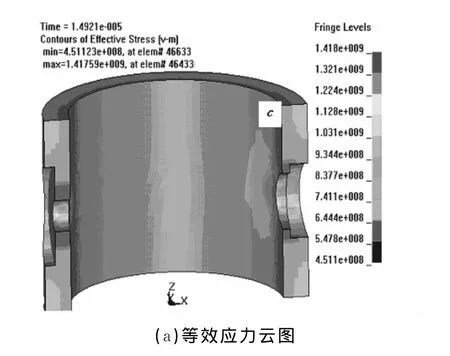
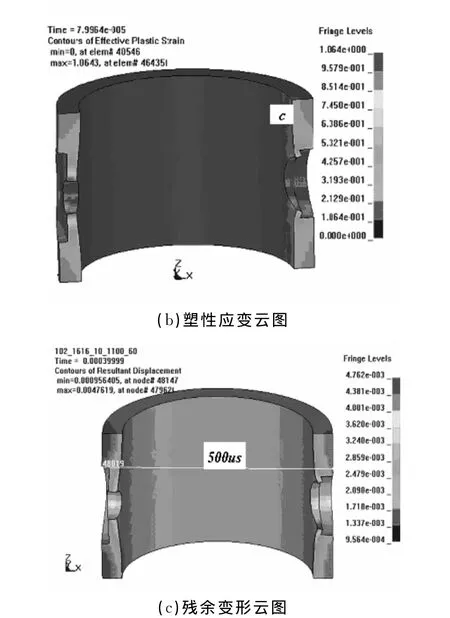
圖6 射孔槍身的應力、塑性應變與殘余變形

圖6（a）為槍身的等效應力云圖，射孔槍結構大部分的應力水平進入塑性應力狀態。從圖6（b）中可以看出最大塑性應變值出現在射流孔和泄壓孔的邊界。當壓力超過彈性極限載荷時，射流孔和泄壓孔從彈性狀態進入塑性狀態，即在內壁出現塑性區。圖6（c）是射孔槍的殘余變形量，可以看到孔口邊界存在的最大變形量為4.8mm。

復合射孔不同裝藥量的爆壓存在差異，這種差異傳導到結構上也對應產生應力、應變和變形的差異。圖7分別繪制了不同裝藥量下的槍身應力、應變曲線，表明在不同的裝藥量下，復合射孔器最大的應力和應變響應關系。

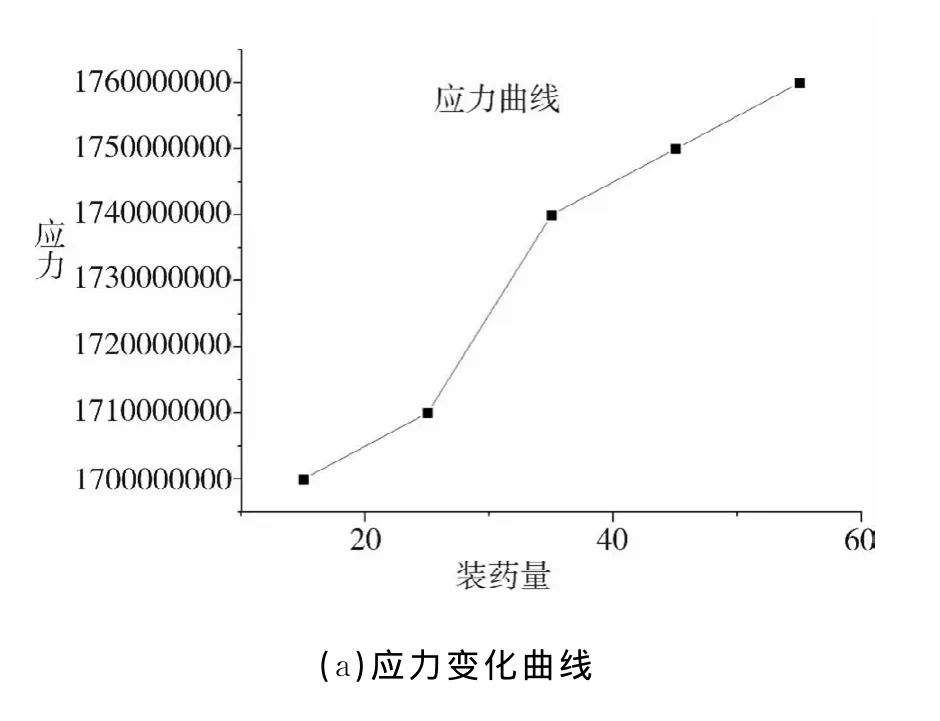
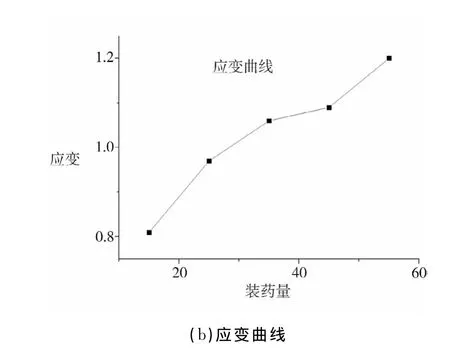
圖7 復合射孔槍結構對裝藥量的影響

4 彈塑性設計準則

4.1 靜態強度設計準則

基于Tresca屈服準則，在不考慮槍身外壁壓力情況下的槍身結構準靜態彈性載荷為：

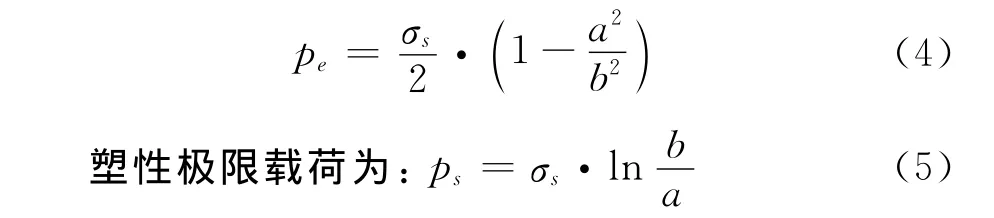
式中a，b為槍身內外徑。槍身材料靜態屈服強度為835MPa的32CrMo4鋼，選用壁厚為10mm的102槍計算，得到在準靜態下射孔槍彈性極限載荷為：Pe＝158MPa，塑性極限載荷為：Ps＝230MPa；槍身材料動態屈服強度為1215MPa的32CrMo4鋼，同樣得到在動態下射孔槍彈性極限載荷為：Pe＝291MPa。Tresca強度理論計算結果比對見表3，從表3可以看出在準靜態載荷條件下對槍身強度設計的最大承載載荷遠遠小于數值模擬得到的載荷，因此用靜強度和動強度準則設計塑性變形的射孔槍，缺乏實際應用意義。

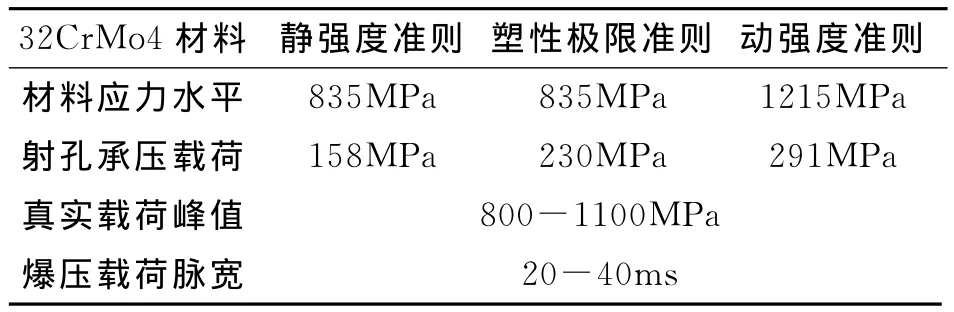
表3 靜強度、動強度、塑性流變設計的極限載荷

4.2 動態塑性設計準則

強度校核結果與數值結果的比較，說明靜強度彈塑設計準則無法應用到復合射孔器的設計之中：靜強度和塑性極限差異大，動強度屈服也不對，因為這里還存在一個時間的因素沒有考慮，因此，需要一個與時間相關的動態塑性流變設計準則。基于沖量守恒定律，射孔槍爆燃所產生的載荷P（t）隨著時間變化，射孔槍身材料動態塑性應變 也隨時間變化。如此，射孔槍身的動態塑性流變設計就應該滿足式（6）的不等式，也就是動態塑性流變設計的新方法。動態塑性設計新方法既然已經提出來，就需要大量的理論細節完善和實驗驗證，最終才能夠成為復合射孔器的動態塑性流變設計準則，也是復合射孔器基礎研究的一個發展方向。

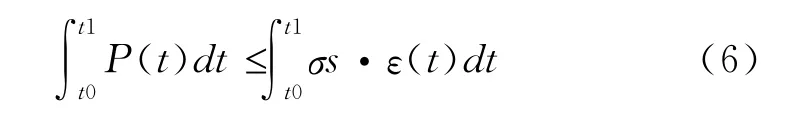
式中，t0、t1為內壓峰值區間的時間區間，σs為槍身材料動態屈服極限；ε（t）為塑性應變。

動態塑性設計新方法既然已經提出來，就需要大量的理論細節完善和實驗驗證，最終才能夠成為復合射孔器的動態塑性流變設計準則，也是復合射孔器基礎研究的一個發展方向。以一個一維塑性變形設計問題為例，則式（6）可以改寫為式（7），具體設計過程仍然離不開結構沖擊變形的數值仿真，需要確定其中應變收斂的時差參數Δt。

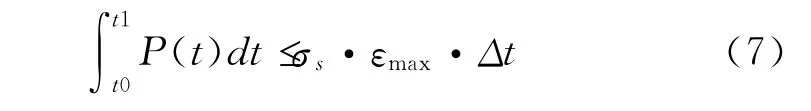
式中的εmax為工程設計許用的最大塑性應變。

5 結語

通過上述的數值研究，得到如下幾點結論：

（1）數值模擬的結果，解釋了裝藥量與爆燃載荷之間正相關的關系，爆壓的峰值和脈寬都隨著裝藥量的增加而增加；其后，火藥持續燃燒的爆燃載荷加大了爆燃載荷峰值的脈寬；

（2）射孔槍在爆燃載荷作用下，應力、塑性應變、變形量主要集中在孔口的縱軸向邊界部位，在射流孔口邊界處應力、應變的變化更為劇烈，槍身從這一點開始發生塑性變形，并隨著壓力的增加塑性區不斷擴大；

（3）靜態載荷與動態載荷對槍身的作用有明顯差異，傳統設計準則不適用于動載荷的強度設計，需要建立新的結構動態塑性流變設計準則。

（4）提出新的設計方法源于沖量守恒理論，細節仍然需要進一步發展，以方便動態塑性設計的應用。

［1］趙莉，趙開良，申梅英，等.不同類型復合射孔器火藥燃燒特征研究［J］.測井技術，2006，30（1）：44－46.

［2］劉會娟，劉蔭忠，田毅，等.復合射孔爆炸與燃燒機理數值模擬分析［J］.測井技術，2012，36（1）：78－83.

［3］趙錚，陶鋼，杜長星.爆轟產物JWL狀態方程應用研究［J］.高壓物理學報，2009，24（3）：277－282.

［4］朱公志，張建為，朱敏捷.石油射孔槍墻體結構優化設計［J］.科學技術與工程，2011，11（25）：6049－6053.

［5］陶亮.射孔槍幾個結構設計問題的數值分析［J］.測井技術，2006，30（1）：25－28.

［6］張昭，劉亞麗，胡海飛，等.射孔槍射孔過程數值模擬及參數控制［J］.塑性工程學報，2008，15（6）：151－156.

［7］王培禹，劉蔭忠，徐波.準靜態下射孔槍的槍身彈塑性理論分析［J］.西部探礦工程，2011，7：70－72.