放慢腳步，聽聽孩子想說什么

吳錫娟

我作為一名中學數學教師，至今有5年多的時間了。我經歷了課堂教學改革的熱潮，參加過課堂變革優質課的競賽，也深深體驗了“今天的新課堂教學改革”。從某種程度來說，的確打破了傳統的課堂教學，讓學生更多地參與到課堂中，但并沒有讓學生真正成為課堂的主人。我也經常會感到很困惑：究竟如何做才能讓學生在課堂上的學習效率更高？為何我認為很簡單的問題，學生卻用疑惑的眼神告訴我：“老師，我聽不懂！”

在一次外出學習中，偶然間看到了一段視頻——“牽一只蝸牛去旅行”，看完之后，深深地觸動了我。在課堂教學不斷改革、不斷創新的今天，雖然大力倡導和推行讓學生成為課堂的主人，試問有多少課堂真正“交給”了學生，讓學生成為真正的主人？是在大型的觀摩課、示范課，還是在優質課的競賽中？教師應該放慢腳步，聽聽孩子想說什么，讓他們成為課堂真正的主人……

于是，我開始讓孩子用自己的思維方式來思考、講解，讓孩子自己站在講臺上，自己解決問題。這讓我看到了他們身上所散發出來的無窮智慧……

在我所教的兩個班級中，有一個班級的學生整體情況較好些，他們的思維很靈活，但是學生的膽子很小，站起來回答問題時都會臉紅，并且語言表達也有問題。所以從一開始我就先訓練他們的語言表達能力和回答問題的膽量。在課堂上，我不在乎講了多少，而是注重聽孩子能說多少、能明白多少。過了一學期，情況好多了：在課堂上，大多數孩子在遇到與別人有不同看法時，能大膽地站起來，流暢地表達自己的想法，也可以在課堂上和我大膽地爭論。每當這時候，看到激情洋溢的孩子，真的覺得他們很棒！在初一下學期的時候，開始接觸簡單的幾何證明題了。對于他們來說，就像無頭的蒼蠅到處亂撞，出現了很多的問題：拿到一個幾何證明題，沒有方向，盲目求證；或者幾何證明過程混亂，更不用說去想多種證明方法。所以一般情況下就是我自己先講，講過之后讓孩子跟著我的思考方向在學生之間相互講解，直到明白為止。同時，在孩子相互講解的過程中，引導他們從不同的角度思考、尋求另外的方法。另外，讓孩子把自己做好的幾何題像改作文那樣相互評改。幫同學改錯，改證明過程，在修改的過程中，能發現別人的問題，也就是糾正了自己的問題。

訓練了一段時間后，在一次數學習題課上，有一個孩子的表現讓我覺得他們智慧無窮。當時我們正在探討一個關于平行線的性質和判定的幾何證明題。題目是這樣的：

■

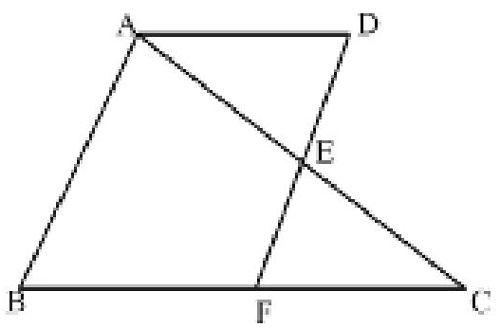
如圖：∠C=∠DAE，∠B=∠D，求證：AB//DF.

對于大多數學生來說，都能想到一種方法進行證明。這時有一個孩子站了起來：“老師，我還有其他方法”。我停了下來，示意讓他說說看，他一說，就說出了5種證明方法，這5種方法如下：

方法一：

∵∠C=∠DAE（已知）

∴AD//CF（內錯角相等，兩直線平行）

∴∠D=∠DFC（兩直線平行，內錯角相等）

又∵∠B=∠D（已知）

∴∠B=∠DFC（等量代換）

∴AB//DF（同位角相等，兩直線平行）

方法二：

∵∠C=∠DAE（已知）

∴AD//BC（內錯角相等，兩直線平行）

∴∠D+∠BFD=180°（兩直線平行，同旁內角互補）

又∵∠B=∠D（已知）

∴∠B+∠BFD=180°（等量代換）

∴AB//DF（同旁內角互補，兩直線平行）

方法三：

∵∠C=∠DAE（已知）

∴AD//BC（內錯角相等，兩直線平行）

∴∠B+∠BAD=180°（兩直線平行，同旁內角互補）

又∵∠B=∠D（已知）

∴∠D+∠BAD=180°（等量代換）

∴AB//DF（同旁內角互補，兩直線平行）

方法四：

在△ADE中，∠AED+∠DAE+∠D=180°（三角形內角和為180°）

∴∠AED=180°-∠DAE-∠D（等式的性質）

又∵∠B=∠D，∠DAE=∠C（已知）

∴∠AED=180°-∠C-∠B（等量代換）

∴∠AED=∠BAC（等量代換）

∴AB//DF（內錯角相等，兩直線平行）

方法五：

∵∠C=∠DAE（已知）

∴AD//BF（內錯角相等，兩直線平行）

∴∠D+∠BAD=180°，∠B+∠BFD=180°（兩直線平行，同旁內角互補）

又∵∠B=∠D（已知）

∴∠BAD=∠BFD（等式的性質）

∴四邊形ABED為平行四邊形

（兩組對角分別相等的四邊形是平行四邊形）

∴AB//DF（平行四邊形對邊分別平行）

當他說完這5種方法時，已經下課了，雖然這節課只講了這么一個題，我卻被這個孩子身上所散發的智慧和能力所折服。特別是第5種方法，他能夠想到利用平行四邊來求證，要知道平行四邊形的性質和判定是八年級才學的，也就是說他能夠利用小學講的有限知識結合現在所學來解決問題！這一節課讓我受到了強烈的震撼：給他們一點時間，聽聽他們想說什么，就會發現孩子真的很棒！

編輯 王夢玉