基于混合博弈的擴展審計抽樣研究

朱佳俊，李金兵，唐紅珍

（1.江南大學 商學院，江蘇無錫 214122；2.北京大學 國家發展研究院，北京 100871）

0 引言

作為審計實施階段中最重要的工作，實質性測試是在符合性測試的基礎上，為取得直接證據而運用檢查、監盤、計算、分析性復核等方法，對被審計單位會計報表的真實性和財務收支的合法性進行審查，以得出審計結論的過程。統計抽樣是實質性測試的基本方式，為審計結論和證據提供技術支持。實質性測試的技術與應用一直是審計研究的重點。GODFREY[1]等從有限和無限總體兩種貝葉斯模型，通過先驗分布確定最佳審計樣本量中的錯誤比率，建立了審計損失與費用的線性效用函數。FELLINGHAM[2]指出在實質性測試中，被審計單位會根據審計師的決策行為選擇相應的策略。NEWMAN[3]分析審計成本和錯誤率的變化對策略的影響，并基于外生方差的正態分布值給出了均衡策略。PATTERSON[4]擴展了隱蔽信息博弈模型，認為審計證據來自正態分布，其參數取決于受審核方提交的資產價值報告及審計師抽檢樣本大小。DIONNE[5]提出了基于隨機抽樣和評分技術的最佳審計策略模型，分析了最佳審計策略與欺詐總成本最小化的關系。GEORGETA[6]提出帕累托審計抽樣法，降低了高估或低估風險導致的審計成本或審計質量的變化。郝玉貴等[7]通過圖解“激勵悖論”，建立了審計收益與成本的博弈模型，闡述了審計監督在實質性測試中的重要性。

變量抽樣是實質性測試中運用的主要抽樣技術。傳統審計變量抽樣多憑主觀經驗估計風險及接受程度，在一定程度上影響了審計抽樣的可靠性及準確性。其原因主要包括：首先，可信賴程度和系數都是主觀經驗估計，與實際審計風險沒有聯系，直接影響抽樣數目和抽樣誤差；其次，由于可信賴程度和系數是根據正態分布查表提取，對于某些特殊或連續的風險接受程度則無法體現；第三，傳統的可容忍誤差率是主觀判斷和設置的，從而在一定程度上影響了計劃、實際及總體抽樣誤差的判斷效果。因此，只有改進變量抽樣的技術和方法，才能真正發揮統計抽樣的效率。

擴展審計博弈是基于貝葉斯理論的延伸審計和判斷的過程,體現了主觀經驗與客觀信息相結合的優點，具有較強的針對性與可行性。本文從混合審計博弈策略和不完全信息出發，構建了基于不完全信息的擴展審計博弈模型，研究擴展審計期望收益與策略矩陣、審計風險類型及關系。將審計風險分析與抽樣技術結合起來，研究基于擴展審計成本和風險的抽樣估計與分析流程，豐富了審計博弈和抽樣技術，對于分析不完全信息下審計風險與成本、可信賴度與抽樣誤差、審計策略與可信區間具有一定的意義。

1 擴展審計博弈策略與風險

在審計博弈中，被審計對象在提供帳目的時候，有選擇“無重大違規”和“重大違規”兩種策略，是否違規反映了被審計對象遵守會計法規與準則的情況，但受審核方總是聲稱提供的帳目沒有違規[8]。審計博弈中，在審計師主要審計完成后作為接受或拒絕后，還可以作出擴展審計的決定。這種擴展博弈其實質就是隱藏行為與不完全信息分析模型，是基于局部沖突和不完全信息的變量總和博弈。

1.1 擴展審計博弈的混合策略

定義1：設審計師接受的概率αc，拒絕的概率為zc，擴展審計的概率為hc，αc+zc+hc=1，擴展審計接受的概率為wc，被審計對象無重大違規的概率為 βc。設0＜C≤E1＜E2＜E3＜E4表示審計師的初始回報，0≤L1＜L2＜L3＜L4表示被審計對象的初始回報。擴展審計時，審計師的額外成本為C，被審計對象不需花費額外成本[9]。審計師和被審計對象的行動構成普通和擴展博弈策略矩陣（見表1），則審計師策略為 Ac=(μc,νc)，其中，μc=αc+hcwc表示審計師擴展接受概率總和，νc=zc+hc(1-wc))表示審計師擴展拒絕接受概率總和。被審計對象策略為Oc=(βc,1-βc)，構成混合策略納什均衡。其中，α,β,z,h,w∈(0，1)。

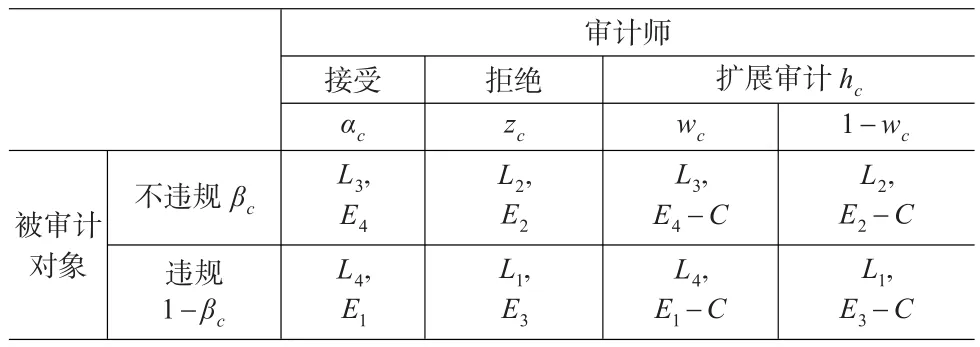
表1 擴展的混合審計博弈策略矩陣

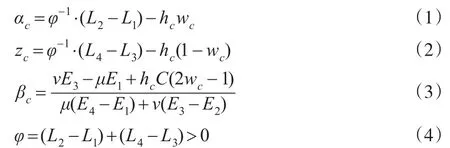
在擴展審計時，被審計對象的回報是不變，而審計師則是有成本C，這樣就會影響雙方博弈策略的變化。特別的，不考慮擴展審計及擴展審計成本時，即當 hc=0且C=0時，有 αc=φ-1·(L2-L1)，zc=1-αc，則：

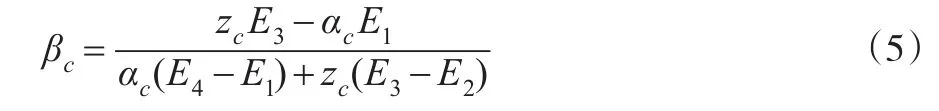
特別的，當α=z=0.5，這時定義1就變成了傳統審計博弈模型[10]。同時，當 βc∈(0，1)時，被審計對象的違規傾向受擴展審計成本的影響，即審計成本越高，被審計對象的違規傾向1-βc就越低。

1.2 擴展審計博弈的審計風險變化

推論1：混合擴展策略納什均衡下，審計師Ⅰ類風險（依賴不足或誤拒風險）為Rc，Ⅱ類風險（過度依賴或誤受風險）為Sc。推論2：混合擴展審計策略納什均衡下，當αc+hcwc=βc時，必然存在Ⅰ類與Ⅱ類風險相同，即Rc=Sc。

同時，當 Rc=Sc，且w≠0.5時，有：

其中，σ=μE4-νE2，τ=νE3-μE1，由于審計師擴展審計成本C＞0，則(L2-L1)σ＞(L4-L3)τ。

擴展審計成本C隨擴展審計接受概率wc的變化而發揮不同的作用。這種成本不僅包含了物質、費用上額外花費，還包括時間、精力上的耗費等；不僅體現了對被審計對象控制測試結果的判斷，也體現了多階段實質性測試的需要。

2 基于擴展審計風險的統計抽樣

傳統的審計抽樣是基于審計風險主觀判斷進行抽樣分析與估計，由于判斷的基礎和條件的不同，以及誤受與誤拒風險雙重設置的需要，很大程度上影響了抽樣結果的真實、有效性。引入擴展審計博弈，可以將動態、量化的審計風險與策略融合到抽樣過程中，為審計抽樣提供系統的風險分析，以擴大審計抽樣的應用范圍。

2.1 可信賴函數與系數

合擴展策略納什均衡下，審計師Ⅰ類風險（依賴不足或誤拒風險）為Rc，根據：

得到可信賴程度RD，查表或直接通過近似插值法求出近似的可信賴系數RFr。近似插值法是根據已有的RD和RFr構建可信賴程度函數，實現對任意插值點RD求RFr。

定義2:設Pk表示所有次數不超過k的多項式的集合。設x0,…xk是一組互異的可信賴程度插值節點，yi=f(xi)為k次多項式插值，使可信賴程度插值多項式Pk(x)∈P滿足：

其中，Pk(x)是可信賴程度插值多項式，f(x)是可信賴程度函數，構成可信賴程度系數插值區間，r(x)是插值余項，(xi,yi)稱為型值點，i=0,1,2,…,k。

定理1:設k次多項式Pk(x)滿足定義2，

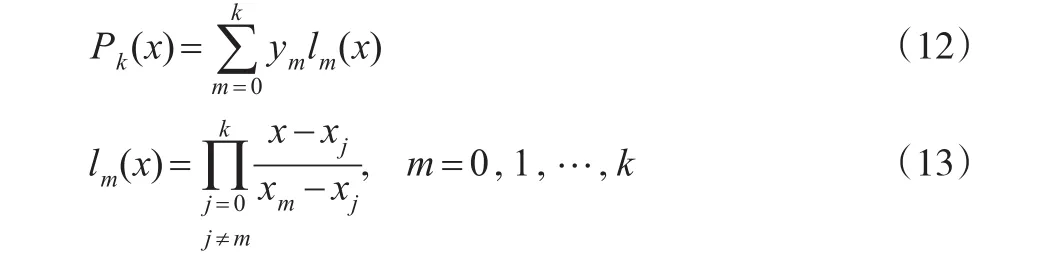
稱Pk(x)式為Lagrange插值公式，lm(x)為插值基函數。

推論3:若可信賴程度函數 f(x)是次數不超過k次的多項式，f(x)的k次Lagrange插值多項式為Pk(x)，則Pk(x)≡f(x)。

基于可信賴程度插值多項式Pk(x)，就可以根據可信賴程度，分別求出可信賴系數RFr和SFa，實現誤拒風險Rc和誤受風險Sc與統計抽樣的連接。

2.2 計劃抽樣誤差與樣本量

計劃抽樣誤差是可容忍誤差與預期總體誤差的差異，是判斷實際抽樣誤差和總體誤差的基礎。傳統的計劃抽樣誤差是根據主觀經驗確定一個誤差比率，誤差比率的優劣直接關系到抽樣的結果。通過引入誤受與誤拒風險的關系變量，以提高誤差比率的有效性。

定義3：設混合擴展策略納什均衡下，審計師Ⅰ類風險（依賴不足或誤拒風險）Rc的可信賴系數RFr，Ⅱ類風險（過度依賴或誤受風險）Sc的可信賴系數SFa，Rc，Sc∈(0,1)，誤拒風險比率（可容忍誤差率）為：

基于審計風險的可容忍誤差率能夠真實反映審計風險的區間，減少主觀估計的差錯，這也是國際上比較公認的方式[11]。通過可容忍誤差率δ與可容忍誤差TM相乘得到計劃抽樣誤差PSR。

按照抽樣的方式，可以得到重復抽樣樣本規模n。n表示樣本量，N表示總體，由于審計抽樣一般采用不重復抽樣的方式，則當時，有修正系數，可以得到不重復抽樣樣本規模n′。

2.3 抽樣區間分析

根據重復與不重復抽樣的要求和實際抽取樣本n′的集中和離散趨勢，可以得到重復與不重復抽樣的實際抽樣誤差 RSR 和 RSR′[12]。

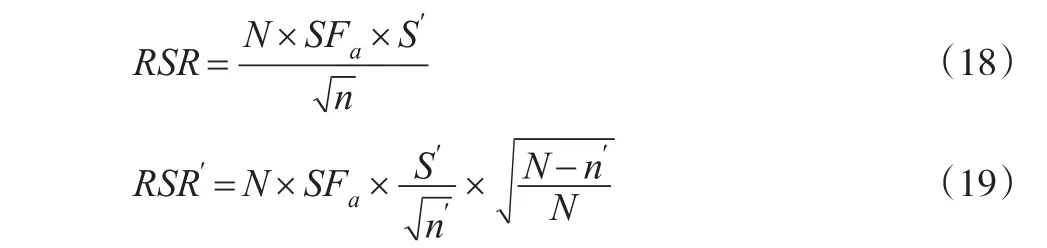
其中，S′表示實際樣本審計價值的標準差，MV表示樣本均值，BV表示總體帳面金額，ETV表示推斷總體金額，可以得到推斷總體誤差PM和總體誤差率PMR。

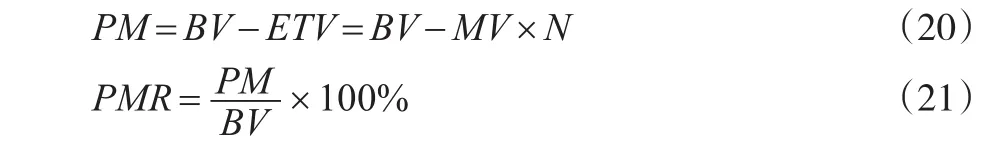
根據推斷總體金額ETV與實際抽樣誤差RSR′，得到抽樣誤差率SER和總體估值區間AI。

當BV∈AI，滿足可信賴度要求，表明被審計項目金額沒有重大錯報。由于誤拒風險Rc是一個動態值，因此，得到估值區間AI也是一個動態區間，可以用來觀察Rc對AI的影響及博弈均衡時的估值區間。抽樣誤差率SER反應了計劃與實際抽樣的差異的程度，總體估值區間AI反映了基于可信賴程度的允許抽樣誤差的絕對值范圍，滿足了從絕對與相對數分析的需求。

3 結論

基于審計風險導向的變量抽樣是通過分析審計師與被審計對象博弈策略與審計風險，對被審計總體進行定量和動態估計，取得總體的數量特征，從而形成對總體的系統判斷，大大提高了應收賬款余額、存貨數量和金額、工資費用、交易活動等項目審計抽樣的效率和效果。該模型的主要作用在于：首先，基于誤拒風險與誤受風險，研究審計抽樣方式與效果，實現了擴展審計博弈的風險分析與統計抽樣相結合，將擴展審計的動態博弈優勢融入到抽樣過程中，為提高審計抽樣的可靠性提供依據；其次，建立可信賴函數，通過Lagrange插值公式，研究可信賴程度與系數，滿足離散和連續插值的需要，擴大了可信賴程度的應用范圍；第三，基于擴展審計博弈，觀察誤拒與誤受風險的變化范圍與均衡條件，建立可容忍誤差率，實現了動態博弈條件下的樣本選擇與誤差估計；第四，通過擴展審計的成本C的變化，觀察統計抽樣的效果與變化情況，掌握擴展審計成本與統計推斷關系，基于擴展審計概率，觀察審計策略的變化區間及其對抽樣方式和樣本規模的影響。

因此，基于混合博弈的擴展審計抽樣是一種理性的判斷和分析方法，審計師通過主要審計狀況決定擴展審計的需求，結合統計數據和先驗概率，確定合理的擴展審計概率wc和擴展審計成本C，能夠有效調節不完全信息下的審計風險與成本，準確設定可信賴程度與風險策略，合理控制抽樣規模與誤差。

[1]Godfrey JT,Andrews R W.A Finite Population Bayesian Model for Compliance Testing[J].Journal of Accounting Research,1982,20(2).

[2]Fellingham J C,Newman D P,Patterson E R.Sampling Information in Strategic Audit Settings[J].Auditing:A Journal of Practice and Theory,1989,8(2).

[3]Newman D P,Noel J.Error Rates,Detection Rates,and Payoff Functions in Auditing[J].Auditing:A Journal of Practice and Theory,1989,(8).

[4]Patterson E R.Strategic Sample Size Choice in Auditing[J].Journal of Accounting Research,1993,31(2).

[5]Dionne G,Giuliano E.Picard P.Optimal Auditing With Scoring:Theory and Application to Insurance Fraud[J].Management Science,2009,55(1).

[6]Georgeta A S,Irimie E P.Mathematical Optimum of the Audit Sample[J].American Journal of Applied Sciences,2012,9(8).

[7]郝玉貴,路云峰.我國國家審計的博弈分析[J].審計研究,2006,(2).

[8]楊羽馨,徐宏毅.政府投資項目代建制下的審計博弈分析[J].武漢理工大學學報,2010,32(18).

[9]Ashutosh D.The Role of Audit Technology and Extension of Audit Procedures in Strategic Auditing[J].International Journal of Applied Quality Management,1999,2(2).

[10]耿修林.決策規則下符合性階段審計抽樣時取樣規模的確定[J].統計與決策,2011,(2).

[11]Baiman S,Evans J,Noel J.Optimal Contracts with A Utility-maximizing Auditor[J].Journal of Accounting Research,1987,25(2).

[12]范麗.淺析審計中的特別風險與審計抽樣[J].財會研究,2012,(9).