波羅的海干散貨運價指數的馬爾可夫鏈分析

畢艷芳

(上海海事大學經濟管理學院，上海201306)

一、引言

波羅的海干散貨指數(BDI)是投資者研究航運股的重要工具，干散貨航運上市公司的股價走勢與BDI緊密相關。波羅的海干散貨市場運價指數即BDI，一直被認為是反映國際干散貨運輸市場變化的晴雨表，同時是初級商品市場價格走勢的風向標。研究BDI的波動規律，對其發展趨勢進行預測得到人們廣泛的關注。呂靖(2002)通過對波羅的海國際干散貨運價指數分別提取長期趨勢項、周期波動項和季節波動項以后，建立ARMA模型，對 BFI(BDI的前身)進行了短期預測［1];徐萍(2005)采用小波分析和神經網絡對BFI進行了預測研究［2];劉晶，盧春霞(2008)結合FFA市場，建立了波羅的海干散貨運價指數ARMA預測模型［3];聶金龍，李序穎(2009)引入ARFIMA模型，來改進傳統的ARMA預測模型［4];靳廉潔(2010)針對巴拿馬型干散貨船舶，進行基于支持向量機(SVM)模型的波羅的海運價指數預測研究［5];魏文臻杰，李序穎(2011)通過引入波羅的海原油運價指數BDTI這一外生變量，提出了一種ARMAX模型的短期 BDI預測方法［6]。

本文將引入馬爾可夫鏈理論，建立BDI的馬爾可夫預測模型，并據此分析BDI的短期波動變化趨勢可能性［7]。

二、數學理論

1.馬爾可夫鏈的定義

將具有“過去只影響現在，而不影響將來”特點的隨機過程成為馬爾可夫過程。狀態離散的馬爾可夫過程稱為馬爾可夫鏈。符合馬氏性的隨機數列可用馬爾可夫鏈進行狀態預測。

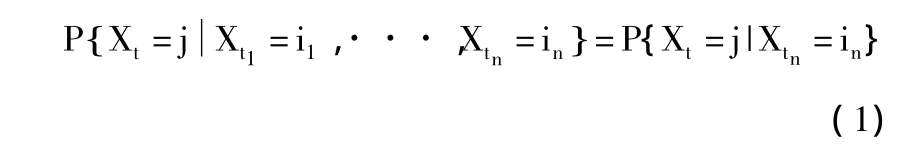
則稱{Xn:n≥0}為馬爾可夫鏈，簡稱馬氏鏈。

隨機過程Xn:n≥{}0是馬氏鏈的充要條件是，對于任意的 n≥1，及任意的 i1，i2，···，in，j∈S，有

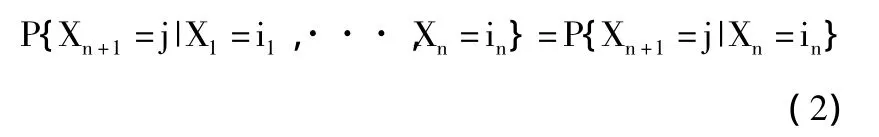
2.轉移概率

對于 馬 氏 鏈{Xn:n≥0}，稱P(ijn)(m)=PS為系統在時刻m時處于狀態i的條件下，經過n步轉移到狀態j的n步轉移概率。P(ijn)(m)具有以下性質:

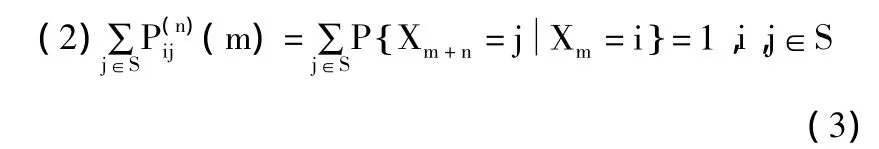
對于齊次的馬氏鏈Xn:n≥{}0，有

轉移概率矩陣形式為

P滿足:(1)所有元素非負，(2)各行元素之和為1。

3.馬氏性的檢驗

檢驗隨機過程是否具有馬氏性，是應用馬爾可夫鏈模型進行數據分析的首要前提。通常對于離散型的馬爾可夫鏈是用χ2統計量來檢驗:

為了說明我們引入頻數矩陣(nij)n×n，nij是系統從狀態i轉移到j狀態的次數。

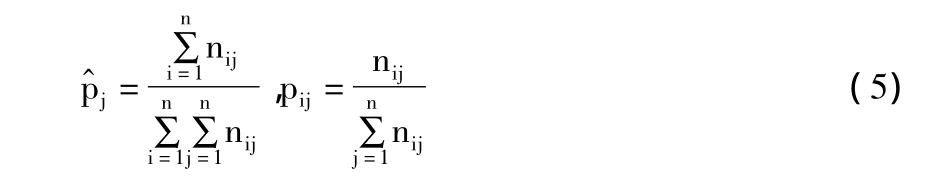
則統計量

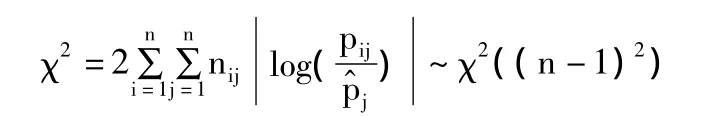
4.C－K方程

對于齊次馬氏鏈{Xn:n≥0}的n步轉移概率，有

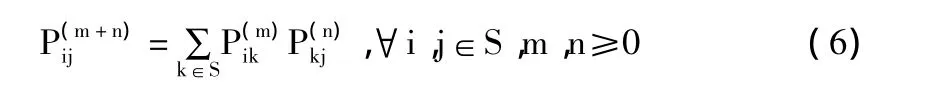
即為C－K方程，在馬爾可夫鏈轉移概率計算中起著重要作用。寫成矩陣形式即:P(m+n)=P(m)P(n)，且P(n)=Pn。所以對齊次馬爾可夫鏈來說，一步轉移概率Pij就可以確定所有的n步轉移概率，即

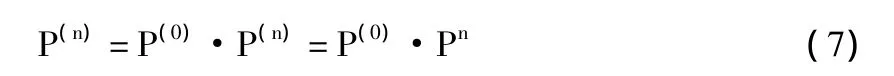
這對于應用馬爾可夫鏈來進行預測有關鍵意義。

二、馬爾可夫鏈分析模型的建立

1.數據選取與狀態劃分

波羅的海干散貨運價指數BDI隨著時間而不斷變化，形成時間序列數據。這里選取2013年12月2日至2014年3月5日的BDI數據(來源Clarkson SIN數據)。

因為BDI一直被認為是反映國際干散貨運輸市場變化的晴雨表，也為簡化分析，將狀態劃分為“上漲”“持平”“下跌”三種狀態［8]，具體劃分法如下:

(1)將BDI數據進行差分處理;

(2)狀態劃分標準:指數上漲超過20點，為狀態1，稱為“上漲”;指數上漲或者下跌在20點范圍內，為狀態2，稱為“持平”;指數下跌超過20點，為狀態3，稱之為“下跌”。故狀態空間S=1，2，{}3。

(3)據上述標準進行狀態劃分，得到如下結果(見表1).

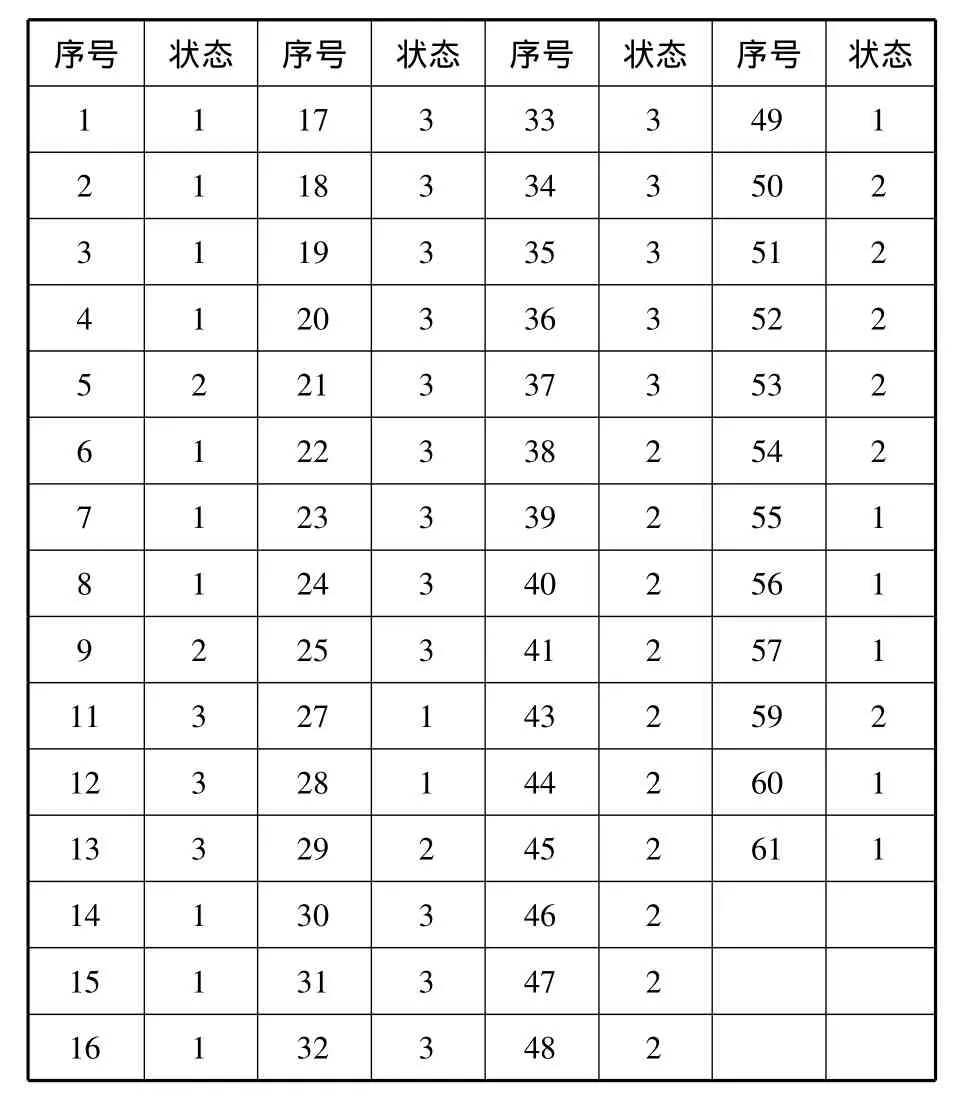
表1 2013年12月2日至2014年3月5日的BDI情況

2.檢驗馬爾科夫性

用nij表示BDI從狀態i轉移到j狀態的次數，通過計算得到頻數矩陣(nij)n×n:

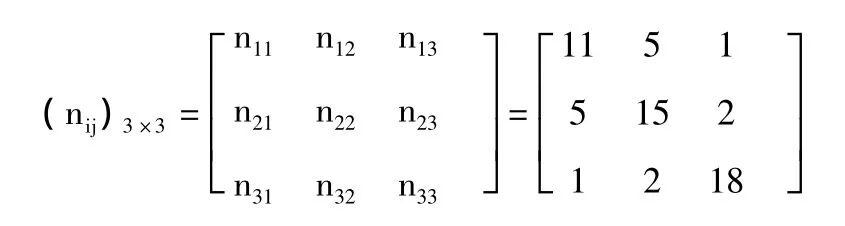
將頻數矩陣的第j列之和除以各行各列的總和，由公式(5)得到，并計算得到

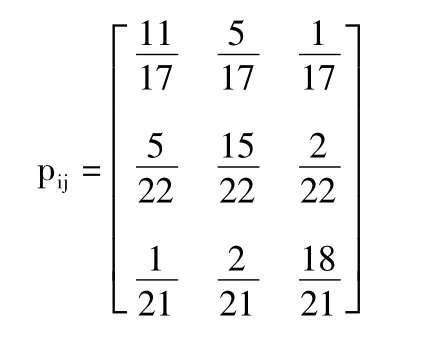
由公式計算得到χ2=60.44257，取α=0.05，查表得χ2(3－1)=5.991，所以此過程是馬氏鏈過程，具有馬氏性［9]。

3.轉移概率矩陣計算

由表1可知，最后一天的狀態為1，而沒有出現狀態轉移，故出現狀態1的次數為18－1=17次，其中由狀態1轉1的次數為11次，即轉移概率;狀態1轉2的次數為5次，即轉移概率;狀態1轉3的次數為1次，即轉移概率同理可計算得到

由此可得，該BDI狀態的一步轉移概率矩陣:

因此利用表1資料預測以后交易日的情況，由于馬氏性和齊次性，我們用第61個交易日的狀態為初始狀態，由表1可知，2014年3月5日的數據落在狀態1區間內，即初始分布為P(0)=(1 0 0 )，利用模型(7)式，可計算得第62個交易日的BDI狀態概率情況:

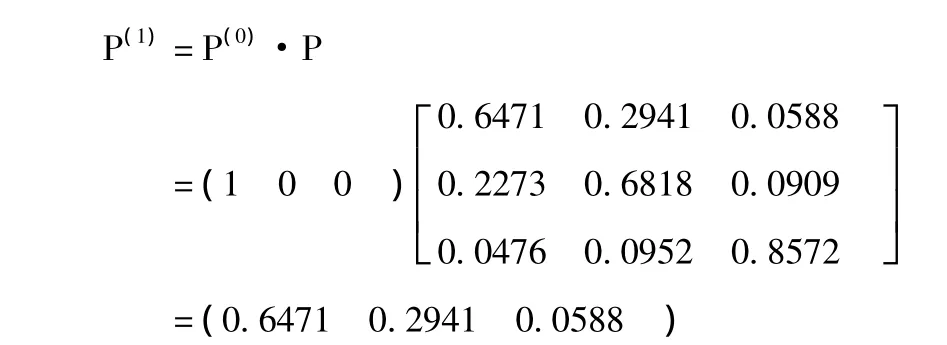
經計算表明，第62個交易日的BDI指數上漲超過20個點的概率為64.71%，指數變動在－20到20范圍內的概率為29.41%，指數下降超過20個點的概率為5.88%。

第59個交易日的BDI狀態概率情況:

第60個交易日的BDI狀態概率情況:

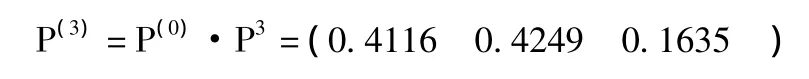
第60個交易日的BDI狀態概率情況:

這樣，只要穩定條件不變，即一步轉移概率不變，以后各個交易日的狀態都可預測分析［10]。

三、馬爾可夫鏈分析結果說明

據以上分析可知，隨著交易日的增加，BDI指數上漲超過20點的可能性在不斷下降，其他兩個狀態出現的可能性在上升，這與現實情況一致。越遠期越是難預測，出現三種狀態的可能性將會差不多。同時，需要說明的是，BDI指數除了受市場因素影響之外，還會受到其他很多外界因素的影響，不能保證轉移概率矩陣不變，因此本方法適宜于對BDI進行短期預測分析，為波羅的海干散貨運價指數的科學預測提供新的思路。

［1] 呂靖.海運價格指數的波動規律［J] .大連海事大學學報，2003(2).

［2] 徐萍.基于小波分析和神經網絡的BFI預測研究［D] .大連海事大學，2005.

［3] 劉晶，盧春霞.波羅的海干散貨運價指數預測模型分析［J] .航海技術，2008(5).

［4] 聶金龍，李序穎.波羅的海干散貨運價指數的ARFIMA模型研究［J] .中國水運，2009(4).

［5] 靳廉潔.基于支持向量機的干散貨運價指數預測研究［D] .大連海事大學，2010(6).

［6] 魏文臻杰，李序穎.基于ARMAX模型的短期BDI預測［J] .物流工程與管理，2012(1).

［7] 李龍鎖 .隨機過程［M] .北京;科學出版社，2011.

［8] 韋丁源.股市大盤指數的馬爾科夫鏈預測法［J] .廣西廣播電視大學學報，2008(9).

［9] 葉宗文.股票價格的馬氏鏈預測法［J] .重慶師范大學學報，2006(3).

［10] 孟銀鳳，李榮華.股票價格的馬氏鏈預測模型［J] .數學理論與應用，2010(9).