潛器在沖擊載荷下的運(yùn)動(dòng)和控制研究

程嘉歡，連 璉，劉可峰

(上海交通大學(xué)海洋工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，上海 200240)

低速潛器往往會(huì)受到?jīng)_擊載荷的作用，從而產(chǎn)生比較復(fù)雜的運(yùn)動(dòng)響應(yīng)，影響任務(wù)執(zhí)行和航行安全。因此，對(duì)其進(jìn)行研究在潛器運(yùn)動(dòng)和操縱性領(lǐng)域有比較重要的意義。

擬研究潛器在水下受到?jīng)_擊載荷時(shí)的運(yùn)動(dòng)響應(yīng)與控制。潛器水下發(fā)射火箭是一個(gè)兩相流動(dòng)和箭體運(yùn)動(dòng)耦合的復(fù)雜問(wèn)題。火箭出筒過(guò)程中，燃?xì)馍淞鲿?huì)對(duì)發(fā)射筒底產(chǎn)生顯著沖擊。火箭出筒后，發(fā)射筒內(nèi)的高溫高壓混氣溢出，由于慣性使筒內(nèi)壓強(qiáng)低于筒外靜水壓強(qiáng)，導(dǎo)致海水倒灌形成“水錘”沖擊筒底。之后在發(fā)射筒內(nèi)形成一系列壓縮波與膨脹波在筒底與筒口之間來(lái)回振蕩，造成潛器受到周期性脈動(dòng)壓力，即水錘效應(yīng)。水錘效應(yīng)會(huì)在火箭出筒后的一段時(shí)間內(nèi)仍對(duì)潛器的姿態(tài)產(chǎn)生持續(xù)影響。

這一課題國(guó)內(nèi)研究與公開(kāi)資料較少。在水下發(fā)射火箭領(lǐng)域，魯傳敬等［1］提出了火箭水下發(fā)射時(shí)箭體與水、燃?xì)獾鸟詈嫌?jì)算方法。李杰等［2］用Rayleih-Plesset方程對(duì)火箭尾部燃?xì)馀葸M(jìn)行建模和模擬。傅德彬等［3-4］利用動(dòng)網(wǎng)格和VOF模型求解燃?xì)狻⑺退魵庵g的耦合，計(jì)算了燃?xì)夂秃Ｋ构鄬?duì)筒底的沖擊壓強(qiáng)。倪火才［5］通過(guò)實(shí)驗(yàn)數(shù)據(jù)定性地分析了水錘效應(yīng)的機(jī)理和規(guī)律。徐新琦等［6］用四元數(shù)方法建立了火箭的水下運(yùn)動(dòng)軌跡模型。在潛器的運(yùn)動(dòng)響應(yīng)與控制方面，陳建軍［7］根據(jù)水錘壓力實(shí)驗(yàn)數(shù)據(jù)簡(jiǎn)單分析了潛器在水錘效應(yīng)下的升沉運(yùn)動(dòng)。李文龍等［8］用Gertier六自由度方程，對(duì)潛器受到發(fā)射沖量后的運(yùn)動(dòng)控制進(jìn)行了仿真。由文立等［9］利用DDAM方法計(jì)算了潛器在沖擊載荷中的響應(yīng)。劉正元等［10］對(duì)低速大攻角運(yùn)動(dòng)的潛水器建立了非解析式數(shù)學(xué)模型。這些研究著重把載荷描述為沖量，忽略了水錘效應(yīng)的后續(xù)影響。至今還尚未發(fā)現(xiàn)有論文系統(tǒng)分析計(jì)算完整發(fā)射沖擊載荷下潛器的運(yùn)動(dòng)規(guī)律與控制。

通過(guò)建立模型潛器在水下的六自由度非線(xiàn)性運(yùn)動(dòng)方程，對(duì)潛器基本運(yùn)動(dòng)進(jìn)行仿真，并通過(guò)仿真結(jié)果和實(shí)驗(yàn)數(shù)據(jù)的比較，驗(yàn)證了數(shù)學(xué)模型的準(zhǔn)確性和有效性。根據(jù)這一模型，系統(tǒng)計(jì)算潛器在水下發(fā)射火箭時(shí)在完整沖擊載荷下的運(yùn)動(dòng)響應(yīng)和控制，并分析機(jī)理和規(guī)律。

1 數(shù)學(xué)模型的建立

1.1 潛器六自由度非線(xiàn)性運(yùn)動(dòng)模型

采用ITTC推薦和SNAME術(shù)語(yǔ)公報(bào)的坐標(biāo)體系［11］，在格特勒潛器標(biāo)準(zhǔn)運(yùn)動(dòng)方程［12］的基礎(chǔ)上，建立潛器六自由度非線(xiàn)性運(yùn)動(dòng)方程組，具體如下。

軸向力方程:

側(cè)向力方程:

垂向力方程:

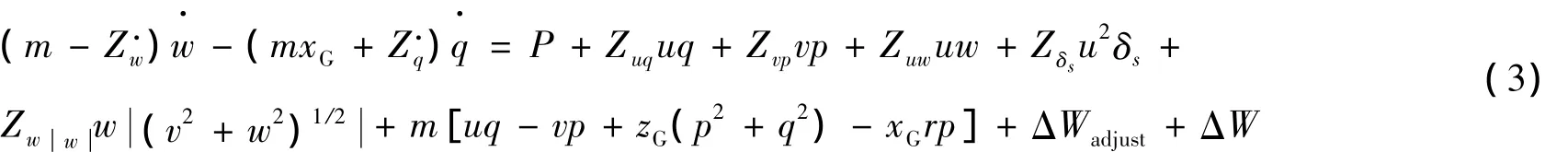
橫搖力矩方程:

縱傾力矩方程:

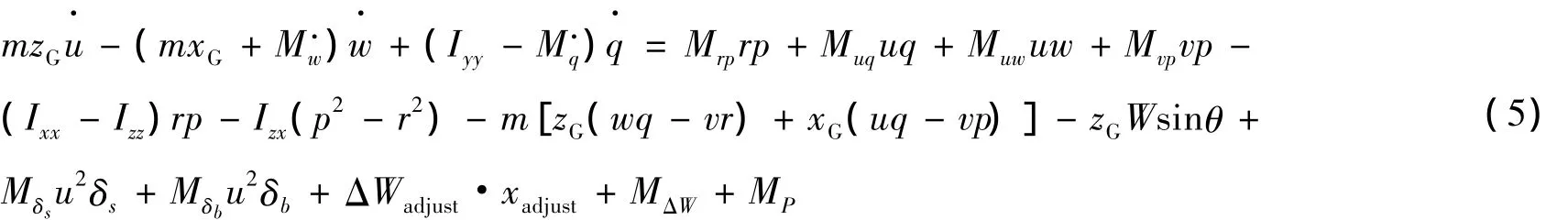
偏航力矩方程:

以上各式中:m為潛器的質(zhì)量，W=mg為潛器在空氣中的重量，B為所受浮力;(xG，yG，zG)為質(zhì)心坐標(biāo)，(xB，yB，zB)為浮心坐標(biāo);u，v，w 為縱向、橫向、垂向速度，p，q，r為橫搖、縱傾、回轉(zhuǎn)角速度;φ，θ，ψ 為橫搖角、縱傾角和首向角，δr，δb，δs分別為方向舵、首水平舵和尾水平舵的舵角，Ixx，Iyy，Izz為潛器在動(dòng)坐標(biāo)中的慣性矩;T為螺旋槳推力，ΔWadjust為潛器浮力調(diào)整水艙的注排水量，xadjust為潛器浮力調(diào)整水艙的縱向坐標(biāo)，ΔW為發(fā)射火箭時(shí)產(chǎn)生的靜載差，MΔW為靜載差引起的縱傾力矩，P為潛器所受發(fā)射載荷力，MP為潛器受到的發(fā)射載荷力矩;其余為潛器的水動(dòng)力系數(shù)，為潛器自身固有屬性。

螺旋槳推力T由螺旋槳的水動(dòng)力性能和轉(zhuǎn)速計(jì)算得到，對(duì)應(yīng)下文2.2中的推力模塊，有:

式中:ρ為水的密度，D為螺旋槳直徑，Ct為螺旋槳推力系數(shù)，n為轉(zhuǎn)速。方向舵與首、尾水平舵舵角δr，δb，δs由下文2.2中的方向舵與水平舵兩個(gè)模塊計(jì)算得出，它們滿(mǎn)足:

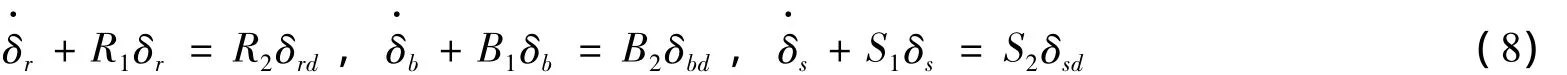
式中:δrd，δbd，δsd為期望舵角，R1，R2，B1，B2，S1，S2為操舵系統(tǒng)固有屬性。由于火箭自重往往與發(fā)射筒進(jìn)水后的重量不同，因此產(chǎn)生靜載差ΔW。

式中:k為發(fā)射火箭總數(shù)，Pwi為發(fā)射第i枚火箭后的進(jìn)水量，Pmi為第i枚火箭自重。潛器通過(guò)浮力調(diào)整水艙的注排水來(lái)平衡靜載差，注排水量ΔWadjust滿(mǎn)足時(shí)間t的線(xiàn)性關(guān)系:

式中:vadjust為注排水速度，TP為火箭發(fā)射的時(shí)間點(diǎn)。

1.2 潛器的受力分析

在發(fā)射火箭的過(guò)程中，潛器的受力主要包括靜力、艇體水動(dòng)力和發(fā)射載荷。前兩者在文獻(xiàn)［13］中有詳細(xì)描述;這里描述發(fā)射載荷，包括發(fā)射反沖力，燃?xì)庳?fù)壓區(qū)和水錘壓力。

1.2.1 發(fā)射反沖力

火箭點(diǎn)火之后，高溫高壓燃?xì)庥蓢娍谶M(jìn)入發(fā)射筒，產(chǎn)生發(fā)射反沖力。發(fā)射反沖力作用于發(fā)射筒底，時(shí)間短，一般僅為數(shù)百毫秒;壓強(qiáng)大，達(dá)到4～8 MPa;隨著火箭出筒迅速衰減。

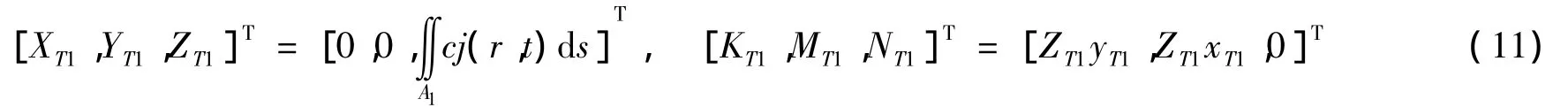
式中:XT1，YT1，ZT1和 KT1，MT1，NT1分別是反射沖擊力和力矩在 x，y，z軸上的分量;沖擊力 cj(r，t)是離發(fā)射筒中心的距離r和時(shí)間t的函數(shù);A1是沖擊力在發(fā)射筒底的作用范圍;xT1，yT1分別是ZT1在x和y方向上的作用力臂。

1.2.2 高壓燃?xì)庠斐傻呢?fù)壓區(qū)

火箭出筒以后，由于慣性，筒內(nèi)的高溫高壓混氣(燃?xì)夂退魵?迅速向外擴(kuò)散，使得發(fā)射筒口附近出現(xiàn)一個(gè)低于周?chē)o壓的負(fù)壓區(qū)。該負(fù)壓區(qū)隨著遠(yuǎn)離筒口而逐漸衰減。

式中:XT2，YT2，ZT2和 KT2，MT2，NT2分別是負(fù)壓區(qū)壓力和力矩在 x，y，z軸上的分量;負(fù)壓區(qū)壓力 fy(r，t)是離發(fā)射筒中心的距離r和時(shí)間t的函數(shù);A2是沖擊力在發(fā)射筒底的作用范圍;xT2，yT2分別是ZT2在x和y方向上的作用力臂。

1.2.3 水錘壓力

在發(fā)射筒口形成負(fù)壓區(qū)之后，在重力和發(fā)射筒內(nèi)外壓力差的共同作用下，海水倒灌入發(fā)射筒，并形成“水錘”沖向筒底，形成水錘壓力。之后形成壓縮波與膨脹波在筒底與筒口來(lái)回振蕩，使?jié)撈魇艿矫}動(dòng)壓力，如圖1所示［5］。水錘壓力曲線(xiàn)是脈動(dòng)的。海水倒灌入發(fā)射筒后的第一個(gè)壓力峰值最大，甚至超過(guò)了火箭發(fā)射時(shí)燃?xì)馍淞鲗?duì)發(fā)射筒的沖擊壓力。隨后壓力峰值明顯衰減，第二個(gè)峰值壓力相當(dāng)于第一個(gè)峰值壓力的一半，之后壓力峰值的衰減減慢，并最終趨向于當(dāng)?shù)氐钠胶鈮毫ΑＣ總€(gè)壓力峰值之間的時(shí)間間隔大體相等，稱(chēng)之為壓力脈動(dòng)周期。

2 實(shí)驗(yàn)?zāi)Ｐ团c仿真模型

采用模型實(shí)驗(yàn)的方式驗(yàn)證數(shù)學(xué)模型的有效性。導(dǎo)入實(shí)驗(yàn)?zāi)Ｐ偷乃畡?dòng)力參數(shù)，建立實(shí)驗(yàn)潛器的運(yùn)動(dòng)仿真模型。通過(guò)對(duì)潛器基本運(yùn)動(dòng)的仿真結(jié)果和實(shí)驗(yàn)數(shù)據(jù)進(jìn)行比較，驗(yàn)證仿真模型的有效性。在此基礎(chǔ)上進(jìn)一步研究發(fā)射火箭時(shí)潛器的運(yùn)動(dòng)響應(yīng)與控制。

2.1 實(shí)驗(yàn)?zāi)Ｐ徒榻B

采用的實(shí)驗(yàn)驗(yàn)證模型利用Thunder Tiger公司的潛器模型改裝而成，參見(jiàn)圖2。

圖1 水錘壓力實(shí)驗(yàn)曲線(xiàn)Fig.1 Test data of water hammer pressure

圖2 實(shí)驗(yàn)?zāi)Ｐ褪疽釬ig.2 Perspective view of the test model

該模型采用電機(jī)推進(jìn)，單槳，安裝有艏舵和十字形艉舵，分別各有一臺(tái)伺服電機(jī)控制尾方向舵和首尾水平舵，安裝電羅盤(pán)和深度計(jì)用于測(cè)量航向和深度。模型的主要數(shù)據(jù)參見(jiàn)表1。

表1 實(shí)驗(yàn)?zāi)Ｐ偷闹饕獏?shù)Tab.1 Principal parameters of test model

該模型潛器的推進(jìn)器是直流電機(jī)，螺旋槳轉(zhuǎn)速n由電機(jī)的Md和螺旋槳扭矩Q決定的:

方向舵和水平舵均視為一階線(xiàn)性時(shí)不變系統(tǒng)，且首尾水平舵同步操作，R1=11.53，R2=10.377，B1=S1=7.69，B2=S2=6.921，根據(jù)式(8)，其傳遞函數(shù)計(jì)算如下:

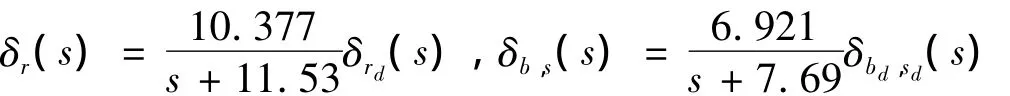
2.2 仿真模型的建立與驗(yàn)證

水動(dòng)力系數(shù)是仿真模型中的關(guān)鍵參數(shù)。根據(jù)文獻(xiàn)［12］第六章的近似計(jì)算方法和文獻(xiàn)［14］的數(shù)據(jù)，測(cè)繪并導(dǎo)入實(shí)驗(yàn)?zāi)Ｐ偷南嚓P(guān)參數(shù)，估算其水動(dòng)力系數(shù)，主要結(jié)果參見(jiàn)表2。

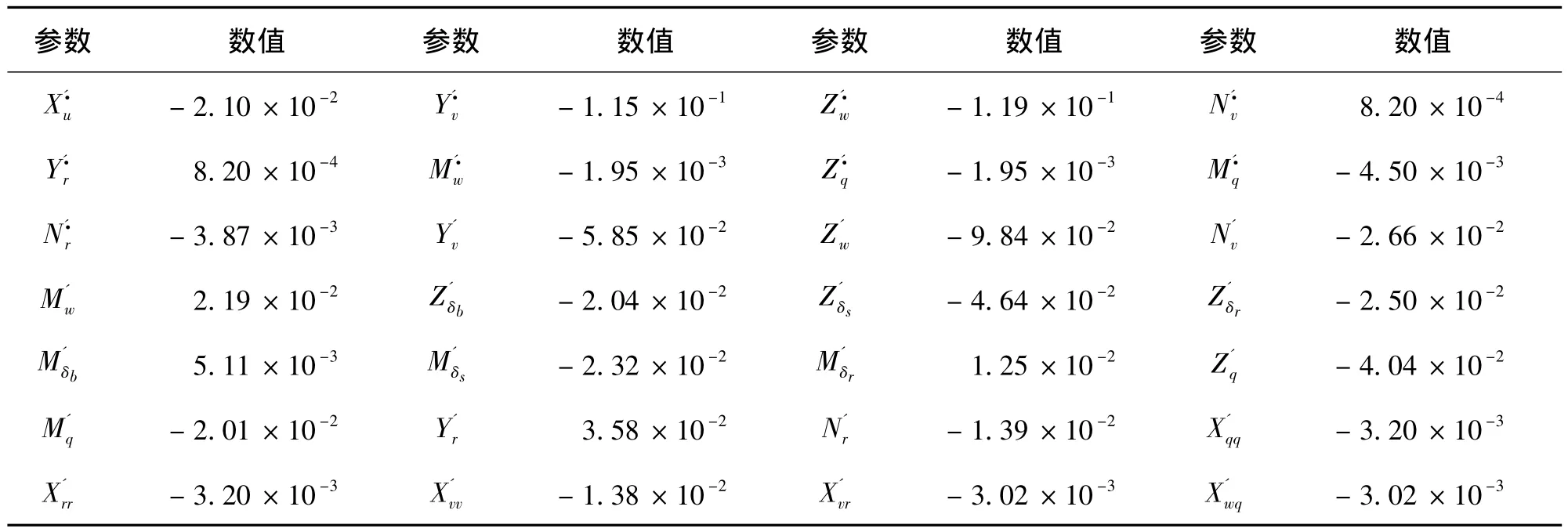
表2 實(shí)驗(yàn)?zāi)Ｐ偷闹饕畡?dòng)力系數(shù)Tab.2 Key hydrodynamic coefficient of the test model

利用Simulink軟件，建立了潛器的運(yùn)動(dòng)仿真模型，如圖3所示。仿真模型中，推進(jìn)模塊輸出推力T，水平舵和方向舵模塊分別輸出控制舵角δb，δs，δr。首尾水平舵同步操作，由于實(shí)驗(yàn)?zāi)Ｐ蜕隙娴霓D(zhuǎn)動(dòng)速度較快，因此其初始操作簡(jiǎn)化為階躍操舵形式，飽和舵角為30°。推進(jìn)系統(tǒng)、方向舵和首尾水平舵均采用PID控制方式。因此控制舵角的響應(yīng)方程滿(mǎn)足:

式中:δb，δs，δr是輸出的控制舵角;ψd，θd是目標(biāo)姿態(tài)角;ψ，θ是目前的姿態(tài)角;KD1，KP1，KI1，KD2，KP3，KI2為PID控制器的參數(shù)。

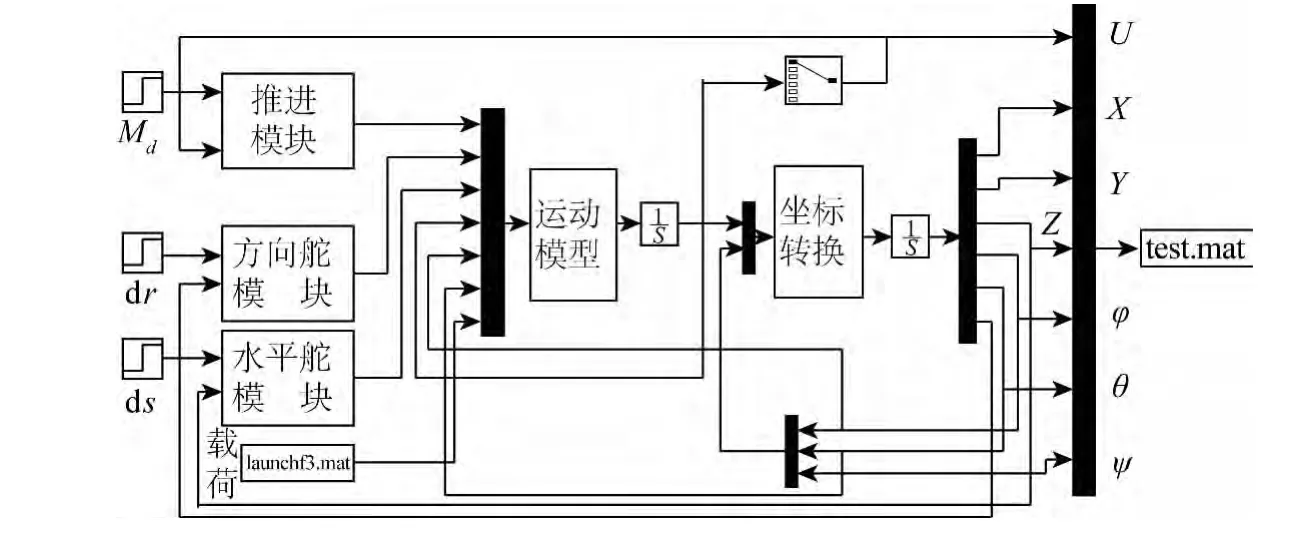
圖3 潛器仿真模型Fig.3 Perspective view of the simulation model of the vehicle

為了驗(yàn)證仿真模型的有效性，對(duì)六自由度基本運(yùn)動(dòng)進(jìn)行了運(yùn)動(dòng)仿真和模型實(shí)驗(yàn)。經(jīng)過(guò)大量實(shí)驗(yàn)確定該實(shí)驗(yàn)?zāi)Ｐ涂刂葡到y(tǒng)的最佳PID參數(shù)，參見(jiàn)表3。在同樣的PID參數(shù)下，用仿真模型對(duì)相應(yīng)運(yùn)動(dòng)進(jìn)行模擬，并將兩組結(jié)果進(jìn)行對(duì)比。

表3 PID控制器參數(shù)Tab.3 Parameters of the PID controller

第一組為水平面運(yùn)動(dòng):定向航行實(shí)驗(yàn)。取目標(biāo)航向?yàn)?60°，航速3 kn，仿真結(jié)果和實(shí)驗(yàn)數(shù)據(jù)如圖4所示。由圖可見(jiàn)，從40 s開(kāi)始，兩者結(jié)果中潛器首向角均在目標(biāo)航向160°附近作小幅振蕩。仿真結(jié)果與實(shí)驗(yàn)數(shù)據(jù)匹配較好，該仿真模型的水平面運(yùn)動(dòng)與真實(shí)情況較為接近。

圖4 潛器定向航行下的時(shí)間—首向角曲線(xiàn)Fig.4 Time-heading angle curve of the submarine under constant-bearing course

第二組為垂直面運(yùn)動(dòng):定深航行實(shí)驗(yàn)。取航速為3 kn，目標(biāo)深度為1 m，仿真結(jié)果和實(shí)驗(yàn)數(shù)據(jù)如圖5所示。如圖，兩者均在60 s左右初次達(dá)到目標(biāo)深度，超調(diào)量在0.1 m左右，仿真結(jié)果收斂速度較快，但兩者的匹配仍然較好。因此仿真模型在垂直面上的運(yùn)動(dòng)也較有效。

圖5 潛器定深航行下的時(shí)間—深度曲線(xiàn)Fig.5 Time-depth curve of the submarine under fixed-depth-way

3 潛器在沖擊載荷下的運(yùn)動(dòng)響應(yīng)與控制研究

假設(shè)模型潛器在水下熱發(fā)射一枚火箭，發(fā)動(dòng)機(jī)噴口總壓8 MPa，燃?xì)鉁囟? 200 K，點(diǎn)火時(shí)發(fā)射筒內(nèi)充滿(mǎn)與外界靜水壓平衡的空氣，火箭在TP=200 s時(shí)從直徑0.55 cm的發(fā)射筒中點(diǎn)火發(fā)射，發(fā)射筒形心位于中縱剖面上，在動(dòng)坐標(biāo)系原點(diǎn)艇艏方向0.1 m處。發(fā)射靜載差ΔW=0.4 kg。參照文獻(xiàn)［4-5］中的受力規(guī)律，發(fā)射單枚火箭時(shí)的載荷曲線(xiàn)如圖6所示。第一個(gè)壓力峰值表示點(diǎn)火時(shí)燃?xì)馍淞鲗?duì)潛器的沖擊壓力，第二壓力峰值為水錘效應(yīng)產(chǎn)生的第一個(gè)水錘壓力峰值，其大小與發(fā)射時(shí)燃?xì)鉀_擊壓力值近似，隨后的波動(dòng)是水錘壓力在發(fā)射筒內(nèi)形成的壓縮波與膨脹波來(lái)回傳播振蕩引起的周期性脈動(dòng)壓力。

3.1 潛器的運(yùn)動(dòng)響應(yīng)

潛器在受到如圖6的沖擊載荷之后，將產(chǎn)生運(yùn)動(dòng)響應(yīng)，包括速度損失、深度變化和縱傾角變化。分別設(shè)定潛器的初始速度為2 kn到4 kn，分別計(jì)算其運(yùn)動(dòng)響應(yīng)和姿態(tài)變化。

圖7所示為潛器的速度損失情況。在火箭點(diǎn)火發(fā)射之后，潛器的速度會(huì)有損失，但在水錘效應(yīng)第一個(gè)壓力峰值之后開(kāi)始恢復(fù)。潛器原有的航速越大，速度損失越小，恢復(fù)速度越快。

圖8所示為潛器的深度變化情況。火箭點(diǎn)火時(shí)潛器受到巨大的發(fā)射反沖力，產(chǎn)生較大的升沉速度，下潛深度迅速增加;之后由于艇體上方負(fù)壓區(qū)的產(chǎn)生和隨之而來(lái)的海水倒灌，深度變化曲線(xiàn)產(chǎn)生較大振蕩;隨著水錘壓力峰值的衰減，深度曲線(xiàn)振蕩幅度減小，最后潛器在一個(gè)新的深度穩(wěn)定下來(lái)。由圖可知，潛器原有的航速越高，深度變化越小，穩(wěn)定深度需要的時(shí)間越少，對(duì)深度保持越有利。

圖9所示為潛器縱傾角變化曲線(xiàn)。在火箭點(diǎn)火時(shí)，巨大的燃?xì)馍淞鳑_擊使得潛器迅速產(chǎn)生較大的首傾角，水錘壓力的第一、第二個(gè)壓力峰值更進(jìn)一步加劇了這一現(xiàn)象。迅速產(chǎn)生的首傾角使?jié)撈魇艿捷^大的反向水動(dòng)力矩的作用，其回復(fù)作用在載荷較大時(shí)并不明顯。在水錘壓力第二個(gè)峰值之后，載荷迅速衰減，潛器的首傾角便在水動(dòng)力的作用下迅速變小，并由于慣性產(chǎn)生尾傾。隨后，在艇體水動(dòng)力和殘存的水錘壓力的共同作用下，縱傾角的振蕩幅度逐漸衰退。潛器的初始航速越高，首尾傾的幅度越小，艇體姿態(tài)保持越好。

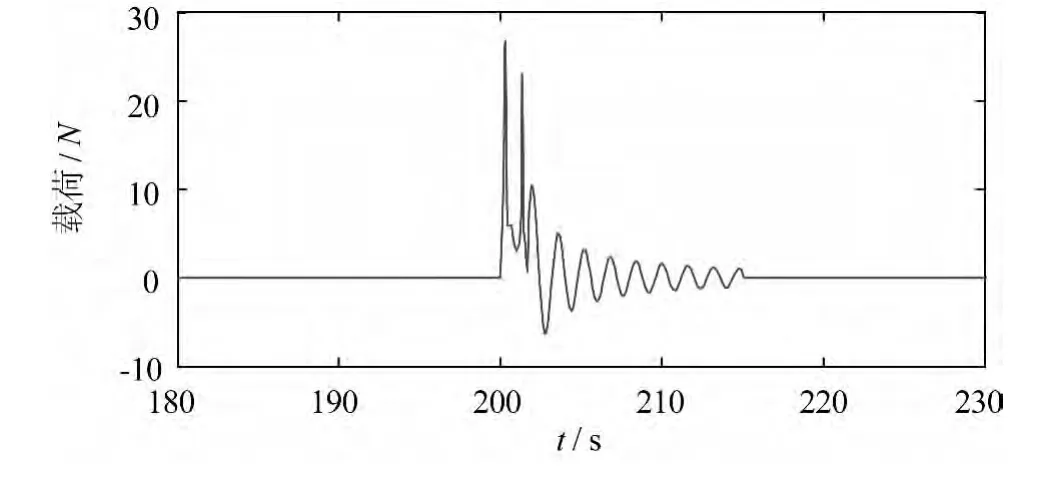
圖6 發(fā)射火箭時(shí)潛器受到的沖擊載荷曲線(xiàn)Fig.6 Impact load curve of the vehicle during the process of rocket launching

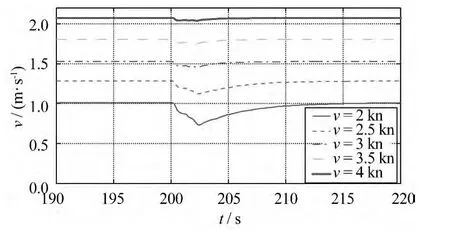
圖7 潛器在水錘效應(yīng)下的速度變化曲線(xiàn)Fig.7 Velocity curve of the vehicle under water hammer pressure

綜上所述，潛器的航速越高，發(fā)射載荷對(duì)潛器運(yùn)動(dòng)的影響越小，這符合現(xiàn)有對(duì)潛器水下發(fā)射火箭的認(rèn)識(shí)和規(guī)律總結(jié)［12］。但是，潛器航速越高，對(duì)火箭水下運(yùn)動(dòng)軌跡和出水姿態(tài)的影響越大，所以潛器在發(fā)射火箭時(shí)的航速選擇是一個(gè)需要平衡的問(wèn)題。

圖8 潛器在水錘效應(yīng)下的深度變化曲線(xiàn)Fig.8 Depth curve of the vehicle under water hammer pressure

圖9 潛器在水錘效應(yīng)下的縱傾角變化曲線(xiàn)Fig.9 Pitch curve of the vehicle under water hammer pressure

3.2 潛器的運(yùn)動(dòng)控制

潛器在受到如圖6的載荷之后，使用舵和浮力調(diào)整水艙對(duì)運(yùn)動(dòng)和姿態(tài)進(jìn)行控制，水艙注排水速度vadjust=2.96×10-2m3/s。設(shè)定潛器的速度為2 kn到4 kn，分別進(jìn)行仿真分析。

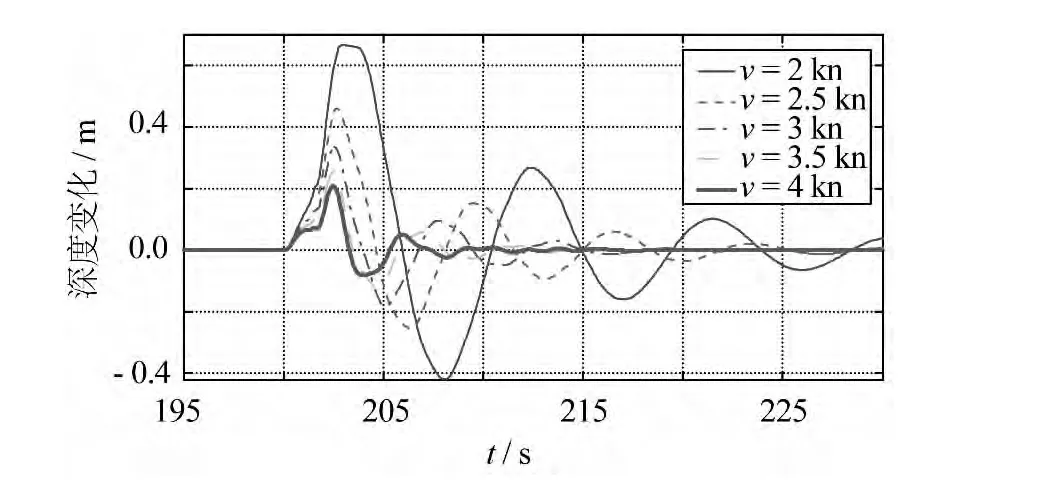
圖10 潛器在控制下的深度變化曲線(xiàn)Fig.10 Depth curve of the vehicle under control

圖10所示為潛器深度變化曲線(xiàn)。由圖可見(jiàn)，在受到發(fā)射沖擊載荷的擾動(dòng)之后，通過(guò)及時(shí)的操控，相比無(wú)控制時(shí)深度變化值明顯減少，在50 s左右的時(shí)間基本恢復(fù)了原來(lái)的深度，控制方式比較有效。潛器的航速越低，控制效果越差，恢復(fù)深度需要的時(shí)間越長(zhǎng)，反向上浮的深度越大。

圖11所示為縱傾角變化曲線(xiàn)。由圖可見(jiàn)，在進(jìn)行控制以后，縱傾角的變化值縮小，能較快恢復(fù)水平狀態(tài)。由于水下火箭發(fā)射對(duì)潛器縱傾角有很高的要求，因此有利于迅速進(jìn)行下一輪發(fā)射。與深度控制類(lèi)似，潛器原有的航速越低，控制效果越差，恢復(fù)水平所需時(shí)間越長(zhǎng)。

圖12為水平舵舵角的變化曲線(xiàn)。由圖可見(jiàn)，為了達(dá)到較好的控制效果，需要舵角作頻率較快的操作。這在模型潛器上比較容易實(shí)現(xiàn)，但是對(duì)于真實(shí)潛器，實(shí)現(xiàn)難度較高。因此，需要輔助動(dòng)力幫助潛器更好的進(jìn)行控制，比如槽道螺旋槳。

綜上所述，可以通過(guò)操作水平舵和浮力調(diào)整水艙對(duì)潛器的運(yùn)動(dòng)進(jìn)行較為滿(mǎn)意的控制。在低速狀態(tài)下，控制效果隨著航速遞增。

圖11 潛器在控制下的縱傾角變化曲線(xiàn)Fig.11 Pitch curve of the vehicle under control

圖12 潛器水平舵的變化曲線(xiàn)Fig.12 Diving plane curve of the vehicle

4 結(jié)語(yǔ)

通過(guò)建立模型潛器在水下的六自由度非線(xiàn)性運(yùn)動(dòng)模型，對(duì)潛器的六自由度基本運(yùn)動(dòng)進(jìn)行仿真，通過(guò)仿真結(jié)果和水池實(shí)驗(yàn)數(shù)據(jù)的對(duì)比，驗(yàn)證了模型的準(zhǔn)確性和有效性。根據(jù)這一數(shù)學(xué)模型，計(jì)算分析了潛器在完整火箭發(fā)射后效(發(fā)射沖擊與完整的水錘效應(yīng))作用下的運(yùn)動(dòng)響應(yīng)和運(yùn)動(dòng)控制。結(jié)果表明，發(fā)射載荷對(duì)潛器的運(yùn)動(dòng)有較長(zhǎng)時(shí)間的顯著影響，潛器的初始速度越大，影響程度越小，影響時(shí)間越短。通過(guò)操舵和壓載水艙的調(diào)節(jié)，可以對(duì)潛器的運(yùn)動(dòng)進(jìn)行較滿(mǎn)意的控制，在一定范圍內(nèi)控制效果隨著初始航速遞增。對(duì)于真實(shí)的潛器，則建議需要加裝輔助動(dòng)力幫助潛器更好的進(jìn)行控制。

［1］ 魯傳敬，陳 芳，樊 泓，等.導(dǎo)彈水下點(diǎn)火的流體動(dòng)力研究［J］.航空學(xué)報(bào)，1992，13(4):B124-B130.(LU Chuan-jing，CHEN Fang，F(xiàn)AN Hong，et al.The fluid dynamic research on the under-water ignition of missile［J］.Acta Aeronauticaet Astronautica Sinica，1992，13(4):B124-B130.(in Chinese))

［2］ 李 杰，魯傳敬.潛射導(dǎo)彈尾部燃?xì)夂笮Ы＜皵?shù)值模擬［J］.彈道學(xué)報(bào)，2009，12(4):6-8.(LI Jie，LU Chuan-jing.The model of combustion gas bubble of submarine-launched missile and numerical simulation［J］.Journal of Ballastics，2009，12(4):6-8.(in Chinese))

［3］ 傅德彬，于殿君，張志勇.氣密條件下水下熱發(fā)射流場(chǎng)數(shù)值研究［J］.固體火箭技術(shù)，2011，34(2):135-160.(FU De-bin，YU Dian-jun，ZHANG Zhi-yong.Numerical simulation of complex flow field for missile launched under-water under gas proof conditions［J］.Journal of Solid Rocket Technology ，2011，34(2):135-160.(in Chinese))

［4］ 傅德彬，于殿君，張志勇.潛射導(dǎo)彈離筒后海水倒灌效應(yīng)數(shù)值分析［J］.固體火箭技術(shù)，2012，35(2):157-160.(FU De-bin，YU Dian-jun，ZHANG Zhi-yong.Numerical simulation of hydrodynamic impact effect after submarine launched missile leaves the launcher［J］.Journal of Solid Rocket Technology，2012，35(2):157-160.(in Chinese))

［5］ 倪火才.潛載導(dǎo)彈水下垂直發(fā)射時(shí)的“水錘”壓力研究［J］.艦船科學(xué)技術(shù)，2000(5):46-49.(NI Huo-cai.Research on water-hammer pressure of under-water missile launching［J］.Ship Science and Technology，2000(5):46-49.(in Chinese))

［6］ 徐新琦，田 兵，李兵尚.潛地導(dǎo)彈水下彈道建模與仿真［J］.彈箭與制導(dǎo)學(xué)報(bào)，2010，30(5):149-152.(XU Xin-qi，TIAN Bin，LI Bing-shang.The model and simulation of submarine to surface missile underwater trajectory［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(5):149-152.(in Chinese))

［7］ 陳建軍.潛載導(dǎo)彈垂直發(fā)射對(duì)耐壓殼體結(jié)構(gòu)的沖擊響應(yīng)分析［D］.哈爾濱:哈爾濱工程大學(xué)，2008.(CHEN Jian-jun.The dynamic response of submarine structure acting by missile impact loads in vertical launch［D］.Harbin:Harbin Engineering University，2008.(in Chinese))

［8］ 李文龍，徐亦凡，李 博.水下連續(xù)發(fā)射導(dǎo)彈時(shí)潛艇與姿態(tài)控制仿真［C］//中國(guó)控制與決策學(xué)術(shù)年會(huì).2004.(LI Wen-long，XU Yi-fan，LI Bo.Simulation of controlling the gesture and depth of ssbn while project in series［C］//Proceeding of 2004 Chinese Control and Decision Conference.2004.(in Chinese))

［9］ 由文立，周方毅，詹發(fā)民，等.艦艇導(dǎo)彈發(fā)射裝置沖擊仿真［J］.艦船科學(xué)技術(shù)，2010，32(9):107-110.(YOU Wen-li，ZHOU Fang-yi，ZHAN Fa-min，et al.Simulation of resistant shock capability of missile launcher［J］.Ship Science and Technology，2010，32(9):107-110.(in Chinese))

［10］劉正元，沈明學(xué)，劉 濤.深水潛器運(yùn)動(dòng)的非解析式數(shù)學(xué)模型［J］.中國(guó)造船，2010，51(2):92-98.(LIU Zheng-yuan，SHEN Ming-xue，LIU Tao.A non-analytic mathematical model of deep-sea submersible［J］.Shipbuilding of China，2010，51(2):92-98.(in Chinese))

［11］ Nomenclature for Treating the Motion of a Submerged Body Through a Fluid［R］.SNAME Technical and Research Bulletin 1-5，1952.

［12］施生達(dá).潛艇操縱性［M］.北京:國(guó)防工業(yè)出版社，1995.(SHI Sheng-da.Submarine Maneuverability［M］.Beijing:National Defence Industry Press，1995.(in Chinese))

［13］劉 鷹，趙 琳.潛艇仿真數(shù)學(xué)模型的推導(dǎo)求解［J］.哈爾濱工程大學(xué)學(xué)報(bào)，1999，20(2):26-33.(LIU Ying，ZHAO Lin.The derivation of submarine simulation math model［J］.Journal of Harbin Engineering University，1999，20(2):26-33.(in Chinese))

［14］尚桂楊.移動(dòng)式水下觀(guān)測(cè)網(wǎng)驗(yàn)證平臺(tái)［D］.上海:上海交通大學(xué)，2011.(SHANG Gui-yang.Development of a testbed of underwater moblie sensing network［D］.Shanghai:Shanghai Jiao Tong University，2011.(in Chinese))