艦船氣泡尾流分布的BPBE表征方法研究

王桂軍，閆雪飛，金良安，苑志江

(海軍大連艦艇學院 航海系，遼寧 大連 116018)

水面艦船在航行過程中會在其尾部一定區域內留下一條長達數千米的具有特殊性質的尾流，其中的氣泡尾流由于可以被尾流自導魚雷探測到，具有重要的軍事和民用價值，是國內外相關領域的一個研究熱點［1］。氣泡尾流可以按離艦船尾部的距離長短劃分為近程尾流和遠程尾流，其中關于遠程靜尾流中氣泡動力學特性的研究屢見不鮮［1］，而專門針對近程湍流尾流的研究報道卻很少見諸文獻。

目前對艦船尾流的氣泡特性研究還主要考慮氣體的傳質因素，而很少有系統考慮聚并影響的。Stewart采用大渦模擬技術(LES)和拉格朗日粒子跟蹤方法(LPD)對尾流環境下的氣泡動力學進行了研究，重點分析了氣體傳質與擴散對氣泡群尺寸演變的影響［2］。陳圣濤采用氣液兩相流模型分別對近程和遠程氣泡尾流含氣量的時間分布特征做了比較全面的數值模擬和實驗研究，指出進程氣泡尾流含氣量以乘冪形式衰減，而遠程尾流基本以指數形式衰減，然而陳的方法過于復雜，體現在占有大量運算內存和時間，一個算例需要在集成計算機上運算3 400個CPU小時［3］。朱東華［4］曾以MINER［5］的初始值生成方法為依據，對尾流的氣泡數密度分布進行了三維數值模擬，基于波爾茲曼型氣泡輸運方程和雷諾平均方程計算出了尾流中不同尺寸的氣泡數密度分布特征，結果表明氣泡尾流主要位于10～200 um之間。劉慧開建立了海洋表層氣泡運動和半徑變化的數學模型，發現小于臨界半徑(74.1 um)的氣泡會迅速溶解，而大于臨界半徑的氣泡會上升到水面破裂，由此得出海水中的氣泡主要以50～74 um之間居多［6］。Carrica采用氣液兩相流技術對艦船尾流中不同位置處的氣含量及氣泡數密度分布進行了數值模擬［7］，但沒有對聚并這一重要因素進行必要的深入分析，而且Carrica的算法同樣要占大量存儲和運算時間(200CPU h)，普通電腦上根本無法實現，難以達到實時應用的要求。

綜上可知，當前關于氣泡尾流的特征研究還存在很多缺陷，對氣泡聚并因素的認識不足。1946年，美國國防研究委員會第六局用聲吶測量了以航速15 kn航行的驅逐艦產生的尾流氣泡分布規律，發現尾流中氣泡直徑為0.08～1.07 mm的氣泡數密度高達5.98×106/m3，如此高的數密度會不可避免導致聚并的發生［8］。此外，Smirnov在對對非動力船只的近程尾流的研究中，也著重分析了氣泡聚并在近程尾流中發生的可能性，提出了氣泡聚并的重要作用，但并未對此進行深入研究［9］。這里在對BPBE方程修正的基礎上，首次將其運用于對氣泡尾流數密度和氣含量的研究上，重點探究了聚并因素的作用，且模型具有簡單，可操作性強的特點，還可節省大量的計算時間(完整模型對3 000 m長度尾流的推演時間不超過4 s)。

1 模型的構建過程

1.1 模型構建的思想與基礎

1.1.1 基本思想

傳統對氣泡尾流的數值模擬將尾流速度與氣泡運動耦合在一起進行求解，大大的增加了模型求解的復雜性和難度，無法滿足軍事應用的實時性要求。鑒于此，采用BPBE方程進行相關求解，可將尾流速度的求解和氣泡特性的計算分開而來，只要有一組準確的速度場，即可模擬其中的氣泡動力學特性，實踐表明，這種思想是可行的，并且可大大的節省時空復雜度。

1.1.2 基礎模型

氣泡群模型是尾流流場的氣泡群聚并模型構建的重要基礎，一個典型的波爾茲曼型氣泡群平衡方程［10］:

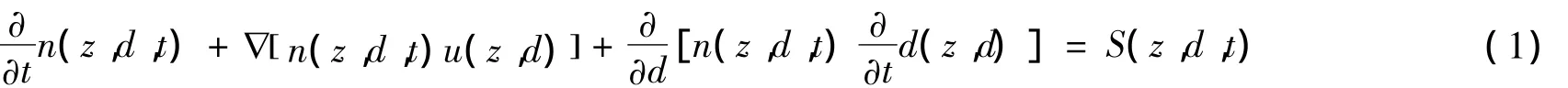
式中:n(z，d，t)為與空間(z)、氣泡尺寸(d)、時間(t)有關的單位體積氣泡數密度函數;u是對應的(z)方向的氣泡速度;d(z，d)為與空間(z)、尺寸(d)有關的表示氣泡尺寸因氣體傳質而引起變化的函數;與氣泡聚并和破裂有關的源項S(z，d，t)可以如下表示:

其中，

分別表示體積小于Vi的氣泡與體積為(Vi-Vj)的氣泡聚并為體積為Vi的氣泡速率，氣泡Vi與其它氣泡聚并而導致氣泡Vi消失的速率，體積為2Vi的氣泡分裂產生兩個氣泡Vi的速率，氣泡Vi本身分裂消失的速率。

與普通的波爾茲曼型輸運方程［4］相比，氣泡群平衡方程的優勢在于不僅包含傳質與擴散項，還包括聚并與分裂項，因此對于氣泡群尺寸的分布與變化描述將更加精確，考慮到實際情況，尾流氣泡尺寸太小幾乎不會分裂，因此文中將忽略分裂的影響。下面將基于氣泡尾流模型對方程(1)進行適當的化簡和離散處理，使其可以用于對艦船尾流的數值模擬。

1.2 模型建立的相關求解

1.2.1 模型的化簡和離散

首先建立尾流場二維坐標系，與航向平行的方向為x，垂直水面向下的方向為y。僅考慮氣泡數密度在軸向x和豎直方向y的變化，空間項可以表示:

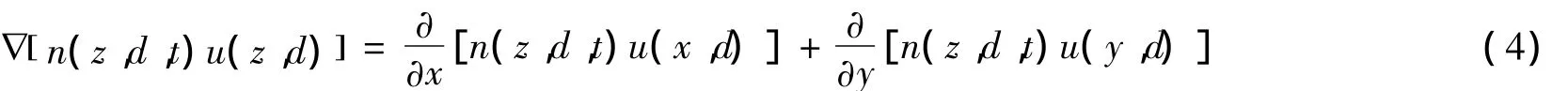
注意到以下兩個關系式:

則有:

對于方程(1)中的擴散與傳質，有:

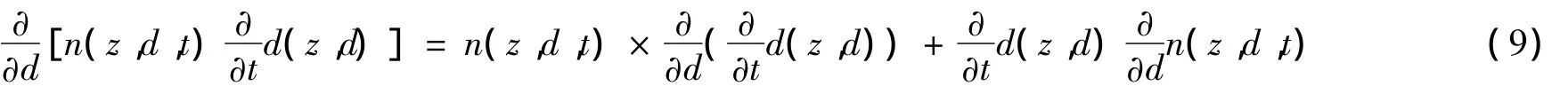
由式(7)可知，時間項可以被消去，因此式(9)可以化簡為:

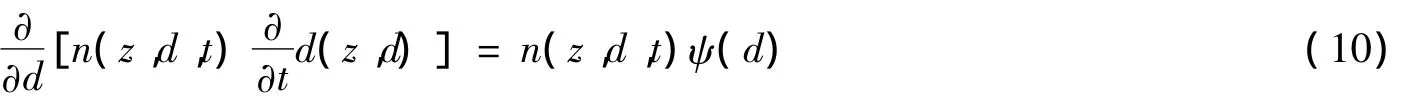
其中，ψ(d)表征擴散與傳質，是關于直徑d的一元函數。

聯立式(1)、(4)、(7)、(8)、(10)，且考慮到氣泡尺寸小到可以忽略分裂項，最終得到如下模型:

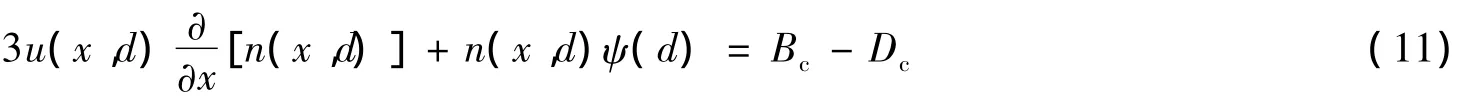
氣泡群平衡方程最終化為只與坐標x和氣泡尺寸d有關的二維偏微分方程，在求解前需要對軸坐標x和氣泡尺寸d進行離散化處理，采用差分法離散后的數值模型:

其中，n(i，j)表示x=iΔx處尺寸為d=jΔd的單位體積氣泡數密度;u(i，j)表示x方向尺寸為d=jΔd的氣泡速度。下面分別給出聚并模型Ω與傳質模型ψ的求解。

1.2.2 聚并模型及其修正

體積分別為Vi和Vj的氣泡集合聚并速率Ωc等于各自密度乘以碰撞概率乘以聚并概率］11］:

其中，碰撞概率θij等于湍流誘導的碰撞概率θijT加上浮力誘導的碰撞概率θijB。上述模型只適用于氣泡數密度小的實驗室水箱或鼓泡塔，而對氣泡數密度巨大的尾流則無能為力，因為ninj后其結果之大完全可以超乎想象，導致碰撞的發生會遠遠大于實際存在的氣泡數，這是與實際明顯相悖的，為此，將其修改為:

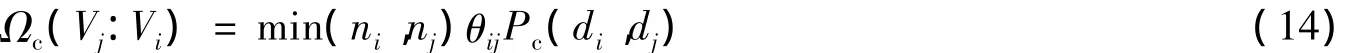
湍流誘導的碰撞概率:

浮力誘導的碰撞概率:

聚并概率:

其中接觸時間［11］:

聚并時間［11］:

上式思想來源于液膜排水模型，其中初始膜厚度h0=5×10-4，破裂液膜厚度hf=1×10-8。兩氣泡的特征尺寸dij:

1.2.3 傳質模型

應用田恒斗［1］建立的艦船尾流氣泡上浮傳質模型:

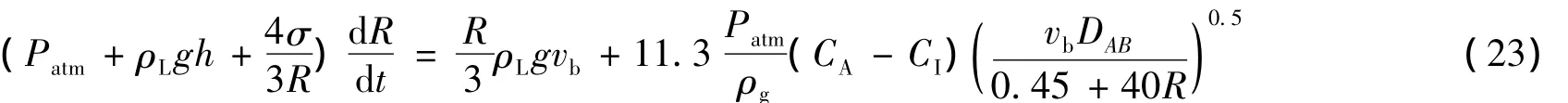
其中，CA為海水中的氣體質量濃度，CI為氣液界面處的氣體質量濃度。

當深度h固定時，對式(23)化簡并對d求偏導即可得到ψ(d)的一元函數表達式。

2 計算與討論

求解尾流場的流動參量的方法可采用MINER［5］提出的方法，在給定船型參數和附件參數(如船長、船寬、吃水、船速、螺旋槳盤面尺寸、槳軸位置等)的情況下，可近似得到尾流空間各點的初始速度、湍動能、湍動能耗散率。根據理論分析和測量經驗，湍流尾流的速度發展變化可以用以下乘冪曲線近似表達［13］:

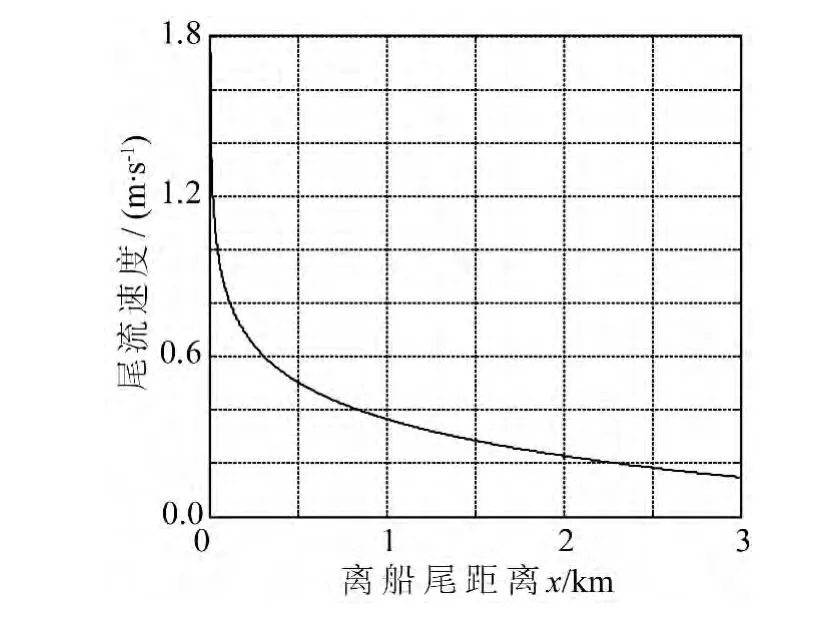
圖1 模擬的尾流速度沿x方向的變化Fig.1 The change of simulated wake speed along x

其中，u0為初始尾流速度，k為待定系數(文中設為5.0)。使用上述方程擬合的尾流速度如圖1所示。由圖可知擬合曲線光滑、連續、穩定，與實際情形較為接近。

計算實例取文獻［3］給出的美國某實船模型，其中各參數具體:船長為86.9 m，船寬為14.6 m，吃水3.6 m，船速為12節，螺旋槳直徑2.44 m。為了進行數值計算，氣泡尺寸需要按照大小進行分組，采用文獻［7］的分組方法，如表1所示。

這樣共得到15個相互耦合的差分方程組。由于要求解氣泡群尺寸沿x方向的分布，又由于氣泡的速度可以用流場速度U近似，因此有u(x，d)=U。模型將在普通臺式機上運行，完整模型的運行時間不超過4 s，相對以往文獻的數值模擬方法大大提高了計算效率，可以達到實時監測的要求。

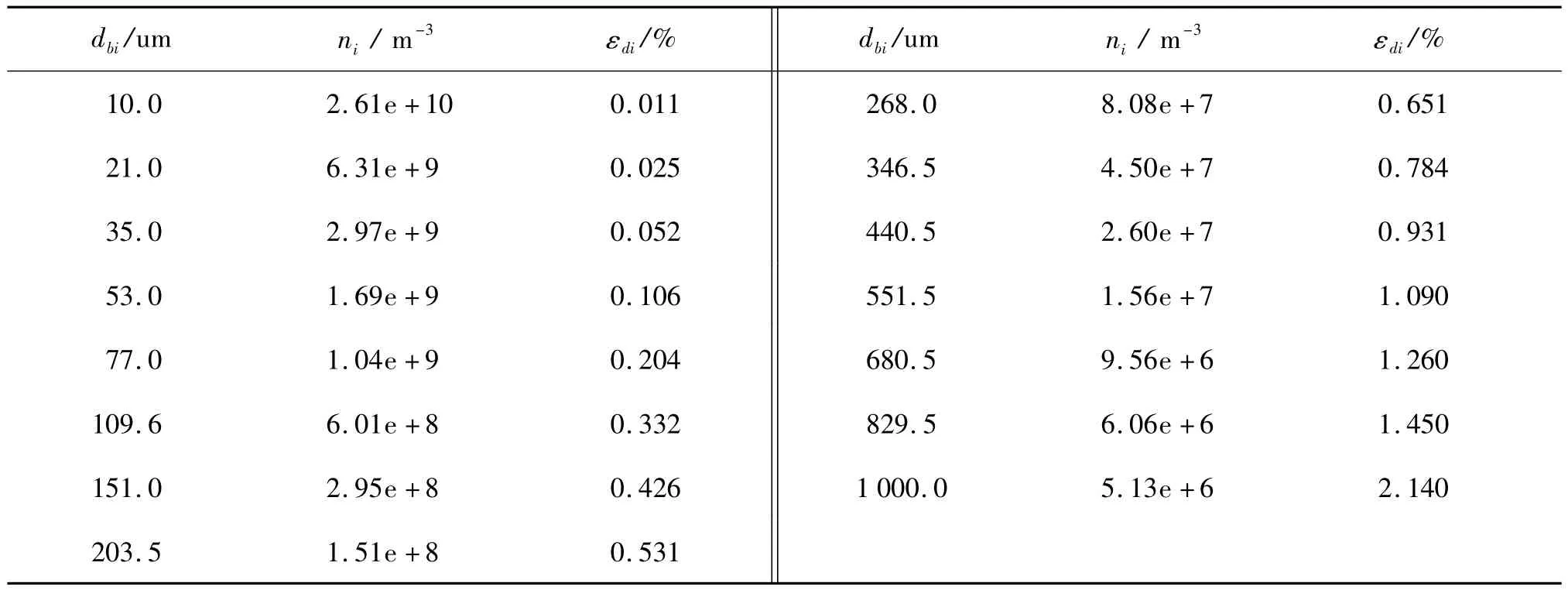
表1 各組分氣泡數密度的初始化Tab.1 Initialization of the bubble-group BND

2.1 沿尾流流向的氣含量分布

首先對沿尾流流向的氣含量分布特征進行求解分析。用于計算氣含量的公式:

這里，由于差分步長Δx設為1 m，因此單位體積VL=1 m3，尾流中總的氣含量表達式:

圖2為只考慮傳質、聚并及二者綜合情形下的尾流中氣含量沿尾流流向的分布。可以看出三種情形下的氣含量總體分布均以乘冪形式進行衰減。相對于傳質因素，聚并作用在近尾流區(小于1 800 m)更加明顯，這是由于近尾流區的船殼、螺旋槳攪動、湍流等因素作用非常強烈，大大增加了氣泡碰撞的幾率，促進了聚并的發生，在聚并的影響下，氣含量衰減曲線更顯陡峭。當進入遠程趨于靜止的尾流區(大于1 800 m)后，氣泡間的影響減弱，聚并作用不再明顯，這時傳質因素開始發揮主要影響，使得氣泡含量繼續以直線方式緩慢減少。

將完整模型的計算結果與文獻［3］的實驗數據進行對比，在比較前，需要將長度單位換算為時間(min)，近似為:

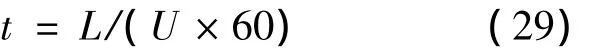
其中，L為尾流長度，U為船速。

此外，由于初始值不同，文中的結果大小會與文獻［3］有所不同(相差約0.1)，因此，為了在同一幅圖中比較，還需各自進行歸一化，歸一化后將文中計算結果與文獻［3］進行對比，如圖3所示。由于文獻［3］的研究分為近程尾流(小于1 800 m)和遠場尾流(大于1 800 m)，因此測量曲線沒有連續，但仍可將其結果與文中氣含量計算值的相應區間進行比較。由圖可知文中計算結果與文獻［3］中氣含量實驗結果曲線的走向吻合較好。

圖4為文中計算的BND沿尾流流向分布與文獻［4］的計算結果的對比。可以看出，雖然增加了考慮聚并因素，仍與文獻［4］吻合較好，進一步表明了文中計算模型的有效性，同時說明聚并對BND的變化影響不大。

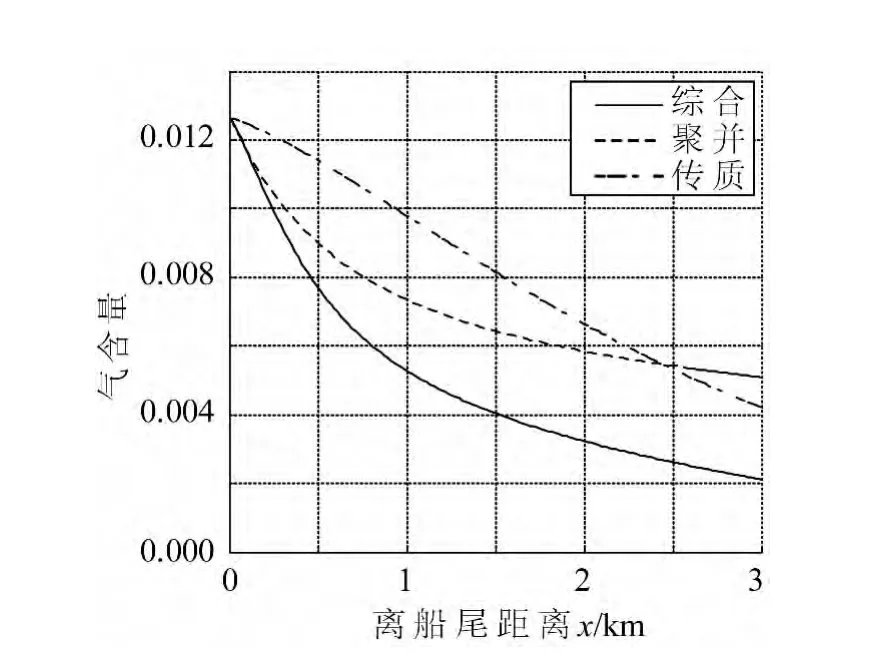
圖2 氣含量沿x方向的變化Fig.2 The change of air content with x

圖3 氣含量隨時間的變化Fig.3 The change of air content with time

圖4 氣泡數密度沿x方向的變化Fig.4 The change of bubble BND with x

2.2 氣泡尾流尺寸的相對分布

下面對氣泡尾流不同尺寸的相對氣含量及BND分布特征進行計算分析。圖5是在分別考慮傳質因素、聚并因素及二者綜合情形下，位于尾流充分發展的遠場尾流區(x=3 000 m)的不同尺寸氣泡BND的相對值分布。由圖可知只在聚并作用下的氣泡數密度值與氣泡尺寸成反比，這主要是由于大氣泡在湍流誘導下的碰撞概率更高，因此聚并消失的速率更大，密度下降也最快。而在傳質作用下，小氣泡由于迅速溶解而消失，大氣泡由于迅速上浮至水面破裂而消失，致使尺寸約為70～80 um的氣泡數密度最大。根據以上結論，綜合情形下的相對BND分布與只有傳質影響下的相對BND分布區別不大。

圖6是位于尾流充分發展的遠場尾流區(x=3 000 m)的不同尺寸氣泡氣含量的相對值分布。由圖可知尺寸200 um的氣泡氣含量最大，這與文獻［7］針對氣泡氣含量相對分布的研究結論是基本一致的。與圖5相比，可知對于只有聚并因素的情形，雖然小氣泡的密度較大，但是由于體積較小，因此氣含量就會相對變小(由表1也可明顯看出)。同時可以看出雖然只在傳質作用與綜合情形下的氣泡相對BND分布比較接近，但是二者氣含量的相對分布卻有較大差異，這說明聚并在氣泡尾流的氣含量分布與變化中發揮著主要作用，不能忽視。

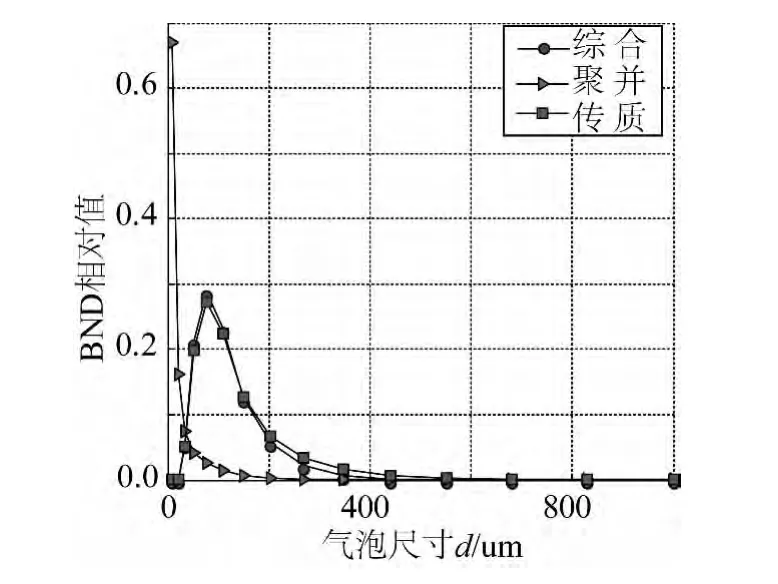
圖5 不同尺寸氣泡相對數密度Fig.5 Relative BND of bubble with different dimensions

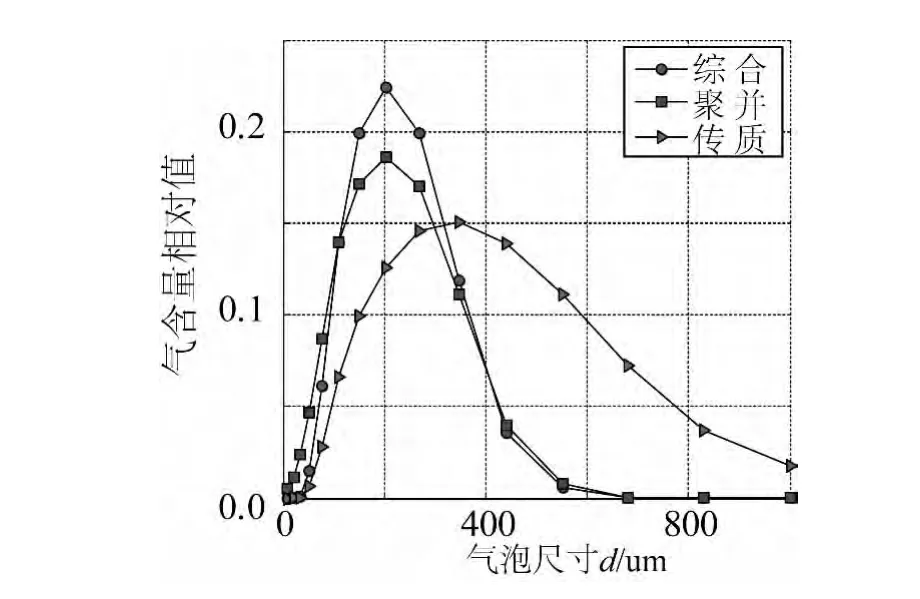
圖6 不同尺寸氣泡相對氣含量Fig.6 Relative air content of bubble with different dimensions

3 結語

氣泡尾流以其強大的制導作用而一直被各國軍界作為研究的重點來對待，鑒于以往對氣泡尾流特征參數的分布研究方面存在的不足，基于BPBE方程提出了可以同時將傳質與聚并作用包含在內的用于氣泡尾流特征分布研究的新思想，并使用數值方法對模型進行了仿真求解，分別對傳質因素、聚并因素以及二者綜合因素情形下氣泡氣含量以及BND的特征進行了分析研究，結果表明聚并在近尾流區作用強烈，而在遠程尾流區傳質起主要作用。聚并對BND的分布變化影響不大，但對氣含量的影響則作用明顯，不可忽視。模型大大提高了計算效率，達到了軍事應用的實時性需求，且結果與相關文獻及實驗數據吻合較好，表明了該模型的有效性。

符合說明:ξ為湍動能耗散率;g為引力常數，10 m/s2;σ為表面張力，0.074 N/m;ρL為海水密度，1 200 kg/m3;Patm為標準大氣壓，105Pa;R為氣泡半徑，m;ρg為氣體密度，1 kg/m3;vb為氣泡上浮速度，m/s;DAB為氣體擴散系數，1.8×10-9m2/s;v為流體粘度，0.001 kg/ms。

［1］ 田恒斗，金良安，遲衛.船舶遠程尾流場中氣泡上浮運動模型［J］.船舶力學，2010，14(11):1195-1201.(TIAN Heng-dou，JIN Liang-an，CHI Wei.Rising process model of bubble in the far wake of ship［J］.Journal of Ship Mechanics，2010，14(11):1195-1201.(in Chinese))

［2］ Stewart M B，Miner E W.Bubble Dynamics in a Turbulent Ship Wake［R］.NRL Memorandmm Report，6055，1987.

［3］ 陳圣濤，王慧麗，王運鷹，等.艦船氣泡尾流特性的數值模擬和實驗研究［J］.船舶力學，2012，16(4):342-349.(CHEN Sheng-tao，WANG Hui-li，WANG Yun-ying，et al.Numerical simulation and experimental study of a ship's bubble wake［J］.Journal of Ship Mechanics，2012，16(4):342-349.(in Chinese))

［4］ 朱東華，張曉暉，顧建農，等.艦船尾流及其氣泡數密度分布的數值計算［J］.兵工學報，2011，32(3):315-320.(ZHU Dong-hua，ZHANG Xiao-hui，GU Jian-nong，et al.Numerical calculation of ship wake and its bubble number density distribution［J］.Acta Armamentarii，2011，32(3):315-320.(in Chinese))

［5］ Miner E W，Ramberg S E.Method for Approximating the Initial Data Plane for Surface Wake Simulation［R］.US:RL-MR-6376，1988.

［6］ 劉慧開，張勸華，楊 立.海洋表層氣泡運動規律的研究［J］.海洋科學，2009，33(1):34-38.(LIU Hui-kai，ZHANG Quan-hua，YANG Li.The study on the motion of bubbles near the ocean surface［J］.Marine Sciences，2009，33(1):34-38.(in Chinese))

［7］ Carrica P M，Drew D，Bonetto F，et al.A poly disperse model for bubbly two-phase flow around a surface ship［J］.International Journal of Multiphase Flow，1999，25(2):257-305.

［8］ 高 江，張靜遠，楊 力.艦船氣泡尾流特性研究現狀［J］.艦船科學技術，2008，30(4):27-32.(GAO Jiang，ZHANG Jing-yuan，YANG Li.The present situation of research on shipwake characteristic［J］.Ship Science And Technology，2008，30(4):27-32.(in Chinese))

［9］ Smimov A，Celik I，Shi S.LES of bubble dynamics in wake flows［J］.Computers＆ Fluids，2005(34):351-373.

［10］Ryszard P W，Moniuk W l，Bielski P，et al.Modelling of the coalescence/redispersion processes in bubble columns［J］.Chemical Engineering Science，2001，56:6157-6164.

［11］Prince M J，Blanch H W.Bubble coalescence and break-up in air-sparged bubble columns［J］.A.I.Ch.E.Journal，1990，36(10):1485-1499.

［12］徐麥容，劉成云.水中浮升氣泡的半徑和速度變化［J］.大學物理，2008，27(11):14-17.(XU Mai-rong，LIU Cheng-yun.The change of radius and velocity of the rising bubble in water［J］.College Physics，2008，27(11):14-17.(in Chinese))

［13］James K E，John R D，Brian A M.The radar image of the turbulent wake generated by a moving ship［J］.London Research and Development，1993，755:343-346.