基于凝集質量法的海洋纜索動力學建模與仿真技術

朱艷杰，朱克強，楊冰卡，王志博，秦道武，曾 峰，章浩燕，夏 峰

(1.寧波大學，浙江寧波 315211;2.寧波市東方電纜股份有限公司，浙江寧波 315211)

纜索目前使用非常廣泛，在世界各處海洋中，有不同形式的海洋纜索。如用于水下電力輸送的水下電纜;用于海洋油氣資源運輸的水下管線;以及用于控制水下潛器或機器人的臍帶纜。其中水下拖曳纜索在海洋工程中是經常使用的設備，在海上作業項目中，占有非常重要的地位。有效的纜索動力分析在很大程度上保證了海上作業的安全。這些纜索的動力分析方法主要可分為三類:有限元法，有限差分法，凝集質量法。

由于纜索動力問題本質上包含大變形和水動力非線性問題，有限元方法的適用性受限:受到方程組的性質影響與邊界條件不能靈活選擇的限制。非線性變系數的控制方程組，最早是使用有限差分法來離散求解的。這一算法經歷了從Sanders［1］忽略了慣性力的纜形三維算法，到Albow和Schechter［2］等人包含慣性力的三維算法，在時空上有限差分離散了該方程組，再到Milinazzo［3］等人改進Albow等人提出的方法，使用Newton-Jacobin法求解形成的非線性方程組，并處理了零張力自由端的問題，一定程度上提高了求解效率，后來Howell［4］和 Tjavaras［5］通過推導纜元受力與變形關系消除了方程的奇異特性，將方程組變成了雙曲型，Grosenbaugh［6-7］采用自適應時間、空間網格步長算法，以及通用α時間積分算法對此方程組進行了改進，進一步提高了差分格式的求解穩定性，使有限差分法更加完善。

與有限差分法從微元的角度出發求解控制方程不同，凝集參數法直接從牛頓第二定律出發，將纜索近似為一系列的節點，節點由無質量的線彈性單元連結，并將連續纜索受到的分布力如重力、流體動力等看作作用在纜的分布節點上，這種簡化的好處是纜索上懸掛浮球或分段連接的纜較容易處理。不同的研究者推導了不同形式的凝集參數法表達式。

采用凝集質量法來分析拖曳纜索回轉形態特征，經和其他研究者用有限差分法給出的拖纜回轉形態以及升沉進行對比，得出凝集質量法也是非常有效的，并且在計算多線列陣時，凝集質量法比有限差分法要靈活很多，所以使用凝集質量法來計算水下纜索動態響應問題，目前看來是一個非常經濟有效的方法。

1 考慮纜索拉壓、彎曲、扭轉變形的通用彈性動力學方程

考慮纜索拉壓、彎曲、扭轉變形y以及附加質量的通用彈性動力學方程［8］為

式中:m1是拉伸后纜索的單位長度質量包括附加質量;s1是拉伸后纜索長度;v=(u，v，w)是纜索的絕對速度;T= (T1，T2，T3)是纜索張力及剪力，下標1、2、3分別表示纜索局部坐標下切向、主法向、副法向三個方向分量，下文同;G是單位長度纜索濕重;D表示流體力。

將變形關系ds1=ds( 1 +e)和質量守恒m1ds1=mds代入上式得:

式中:m是未拉伸纜索的單位長度質量;e是應變。在局部坐標(τ，n，b)下對向量求導滿足下面的法則:局部坐標下對向量 f=(fι，fn，fb)關于 s，t求導分別為:

考慮纜索附加質量，在局部坐標中展開:

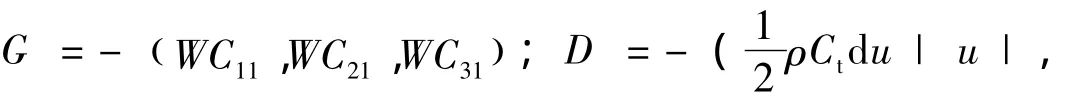
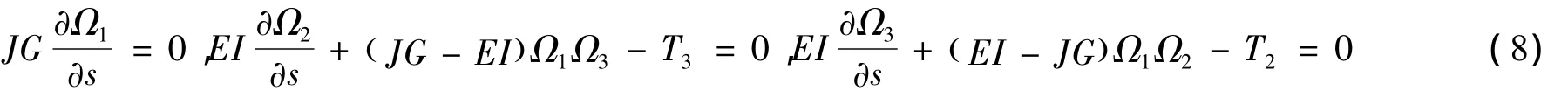
Hover［10］發現了四元數，用它來代替歐拉角，可以避免奇異性問題，下面是四元數和歐拉角之間的轉換關系。

四元數［8］:β0=cos(γ/2)，β1=lxsin(γ/2)，β2=lysin(γ/2)，β3=lzsin(γ/2);其中， lx，ly，l( )

z為瞬軸(在某瞬時，剛體上絕對速度為零的點與原點的連線稱為瞬軸)，γ為剛體繞瞬軸旋轉的角度。二者的轉化可參考文獻［11］。

2 利用凝集質量法離散方程

對上述通用方程(1)，已有研究者利用有限差分法進行離散，文中用凝集質量法來離散，并考慮纜索的附加質量，基本思想參考文獻［12］，第k個節點的方程離散為

3 仿真算例

下面給出一個仿真算例來驗證此離散方法的有效性。拖曳系統如圖1所示，拖船以9.52 m/s速度直航1 s，然后進入半徑640 m的回轉運動440 s，最后，在完成375°的回轉后，沿圓周的切線直線運動300 s。所選用的纜索數據參數如表1來自文獻［3］。拖曳系統分為24個節點，拖纜系統由豎直靜止狀態以9.52 m/s速度直航足夠長的時間達到穩定狀態，以此穩態解作為回轉的初始姿態。圖2和圖3給出了計算結果和文獻結果的對比，由對比顯示兩者結果具有一致性，說明文中計算結果是可靠的，即凝集質量法是有效的。

圖1 拖曳系統Fig.1 Towed system

表1 纜索參數Tab.1 Physical properties of cable

圖2 回轉平面計算結果對比Fig.2 Plan view of circular manoeuvre

圖3 回轉側視計算結果對比Fig.3 Profile view of circular manoeuvre

從表2中看出，文中得出的初始深度、最低深度和最后深度均在有效范圍之內，并且最低深度與實驗值誤差最小，由此可見，凝集質量法計算纜索動態響應問題，也是很有效的，并且比有限差分法靈活簡便。所以在研究此類問題時，凝集質量法是一個不錯的選擇。

表2 文中數據和文獻［3］中數據比較Tab.2 Comparison of this paper’s and the literature［3］’s data

4 結語

1)本模型對回轉的模擬，最大下沉深度與實驗值誤差，是目前已經發表的幾種方法中最小的一個，因而對拖纜回轉時觸底問題具有重要參考價值;

2)研究表明除了低張力、小回轉半徑等曲率時間變化率大的運動之外，纜索彎曲剛度，對纜索曲率時間變化率小的運動，影響不明顯;

3)在坐標轉換中用四元數代替歐拉角，可以克服歐拉角轉換的奇異問題，剔除大量的運動不連續點，更光滑的預報纜索空間運動，應該在未來的纜索動態模擬中引起重視。

［1］ Sanders J V.A three-dimensional'dynamic analysis of a towed system［J］.Ocean Engng，1982，9(5):483-499.

［2］ Ablow C M，Schechter S.Numerical simulation of undersea cable dynamics［J］.Ocean Engng，10(6):443-457.

［3］ Milinazzo F，Wilkie M，Latchman S A.Anefficient algorithmfor siumlating the dynamicsof towedcable systems［J］.Ocean Engng，1987，14(6):513-526.

［4］ Howell C T.Investigation of the dynamics of low-tension cables［D］.Massachusetts Institute of Technology/Woods Hole Oceanographic Institution，1992.

［5］ Tjavaras A A，Triantafyllou M S.Non-linear response two disordered pendula［J］.Journal of Sound and Vibration，1996，190(1):65-67.

［6］ Gobat J I，Grosenbaugh M A.Time-domain numerical simulation of ocean cable structures［J］.Ocean Engineering，2006，33(10):1373-1400.

［7］ Grosenbaugh M A.Transient behavior of towed cable systems during ship turning maneuvers［J］.Ocean Engineering，2007，34(11-12):1532-1542.

［8］ John B Herbich.Developments in Offshore Engineering［M］.Gulf Publishing Company，1998.

［9］ Christopher Todd Howell.Investigation of the dynamics of low-tension cables［D］.Massachusetts Institute of Technology，1993.

［10］Franz S Hover.Simulation of stiff massless tethers［J］.Ocean Engineering，1997，8(24):765-783.

［11］陳志明，王惠南，劉海穎.全角度歐拉角與四元數轉換研究［ED/OL］.http://www.paper.edu.cn，2012-12-11.(CHEN Zhi-ming，WANG Hui-nan，LIU Hai-yin.Research on Large-scale Transformation Algorithm of Quaternion to Euler Angle［ED/OL］.http://www.paper.edu.cn，2012-12-11.(in Chinese))

［12］ ZHU Ke-qiang，CAI Ying，YU Chun-ling，et al.Nonlinear hydrodynamic response of marine cable-body system undergoing random dynamic excitation［J］.Journal of Hydrodynamics，2009，21(6):851-855.