基于自適應(yīng)模糊邏輯的活塞發(fā)動(dòng)機(jī)TCU故障檢測(cè)算法研究
熊云濤,唐榮澳,劉愛(ài)兵
(1.中航工業(yè)洪都,江西南昌330024;2.電子科技大學(xué)航空航天學(xué)院,四川成都611731)
0 引言
開(kāi)展活塞發(fā)動(dòng)機(jī)TCU地面試車及故障診斷研究,對(duì)于確保試飛安全具有重要意義。發(fā)動(dòng)機(jī)故障自動(dòng)檢測(cè)本質(zhì)上屬于模式識(shí)別問(wèn)題[1],即通過(guò)計(jì)算機(jī)自動(dòng)完成復(fù)雜的數(shù)據(jù)分析工作,實(shí)現(xiàn)發(fā)動(dòng)機(jī)狀態(tài)的分析與判斷。近年來(lái),現(xiàn)代故障檢測(cè)理論和算法不斷完善和拓展,建立了基于信號(hào)處理、統(tǒng)計(jì)、人工智能等的多種故障檢測(cè)新理論和新方法[2-3],包括:模糊邏輯法、頻譜分析法、狀態(tài)模型辨識(shí)法、隨機(jī)模型參數(shù)法、專家系統(tǒng)法等。[4-5]
為檢測(cè)發(fā)動(dòng)機(jī)運(yùn)行狀態(tài)及故障分析,本文通過(guò)分析模糊邏輯系統(tǒng)的數(shù)學(xué)原理及其自適應(yīng)學(xué)習(xí)算法,引入模糊邏輯算法,建立了基于模糊邏輯的故障診斷方法,并利用MATLAB軟件實(shí)現(xiàn)了該模塊功能,經(jīng)分析獲得了一些參考結(jié)果,為實(shí)現(xiàn)對(duì)發(fā)動(dòng)機(jī)TCU運(yùn)行狀態(tài)監(jiān)控與分析奠定了基礎(chǔ)。
1 自適應(yīng)模糊邏輯數(shù)學(xué)原理
設(shè)備故障檢測(cè)存在著不確定性,這種不確定主要表現(xiàn)在隨機(jī)性和模糊性兩個(gè)方面[7]。隨機(jī)性是由于事物的因果關(guān)系不確定造成的。模糊性是指事物在質(zhì)上沒(méi)有確切的含義,在量上沒(méi)有明確的界限,造成亦此亦彼的性態(tài)。為了解決在設(shè)備檢測(cè)中存在的邏輯和數(shù)值上的邏輯性現(xiàn)象,采用了模糊數(shù)學(xué)的描述方法。模糊數(shù)學(xué)在精確數(shù)學(xué)的基礎(chǔ)上進(jìn)行了延伸和推廣,能夠描述事物的不確定性現(xiàn)象。
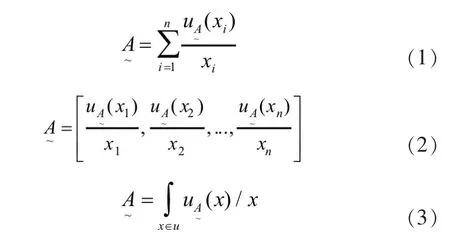
以上所述模糊集合是針對(duì)某單個(gè)論域而言的。……

