多變量耦合系統PID神經網絡控制方法研究
朱 林,吳冬雪,趙 倩
ZHU Lin1, WU Dong-xue1, ZHAO Qian2
(1. 內蒙古科技大學 信息工程學院,包頭 014010;2. 中海石油海南天然氣有限公司,海口 578001)
0 引言
以多變量、強耦合、非線性為特點的復雜工業過程控制,一直是控制理論與控制工程領域的研究熱點和前沿。復雜工業過程控制由于數學模型變量多、變量間耦合、非線性和高階,相應控制器設計困難。
在工業控制中,PID控制一直是通用、有效的控制方法[1]。但是,面對多變量、強耦合、非線性為特點的復雜工業過程,PID控制效果會變差甚至不可控。神經網絡具有很強的自學習、自適應和任意非線性表達能力,近年來逐漸應用于復雜系統的控制中。當系統存在不確定性因素時,更能體現神經網絡的優越性。文獻[2]以二變量耦合時變系統為對象,設計了一種PID神經網絡模型。該模型與用神經網絡對PID控制器參數進行輔助修改的方法有本質的區別[3,4]。應用PID神經網絡控制時,無需為對象的參數和系統結構進行辨識,可根據對象參數變化時對系統輸出的影響,“在線”地調整PID神經網絡的權值,較好地解決了多變量、耦合系統的控制難題。
但是,PID神經網絡中權值采用梯度學習算法,初始權值隨機給定,造成網絡權值修正較慢且容易陷入局部最優,為了達到滿意的訓練效果,需要多次的給定,而給定的方法并不能保證每次給定均能達到期望控制效果[5]。為改善上述不足,筆者分析研究了用遺傳算法、蟻群算法等方法優選PID神經網絡的初始權值的可行性,研究發現,遺傳算法對PID神經網絡初始權值優化效果較好。本文以三輸入、三輸出、非線性、耦合系統為控制對象,設計構建了優化初始權值的PID神經網絡。同時,為了提高PID神經網絡學習效率和預測精度,在網絡權值修正算法中加入了動量項。MATLAB仿真結果證明:該方法在提高控制精度,精確解耦方面效果好。
1 多變量非線性強耦合系統
設被控對象具有多變量、非線性、強耦合的性質,共有3個輸入,3個輸出,系統的傳遞函數如下:
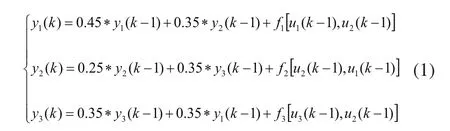
其中非線性函數為:
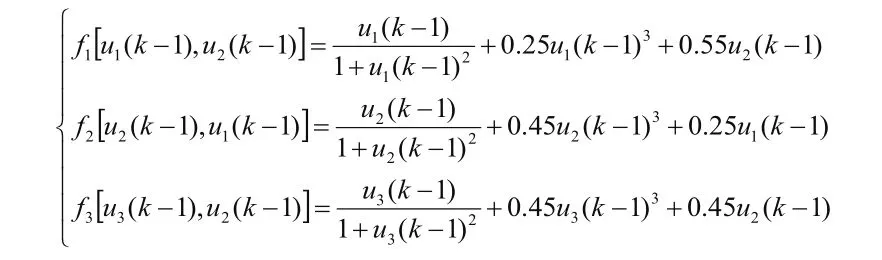
由于該系統的特點,采用傳統的PID控制器很難得到理想的控制效果。
2 遺傳算法優選初始權值的PID神經網絡解耦控制器
根據上述被控對象特點,PID神經網絡解耦控制器設計為6×9×3的三層前向網絡,即3個并列的子網絡。控制系統結構如圖1所示。各層的輸入、輸出函數見文獻[6],本文不再贅述。
圖1中,xs1、xs2、xs3為系統被控量的給定值;u1、u2、u3為被控對象的輸入;y1、y2、y3為被控量當前值;wsij為輸入層至隱含層的連接權值;w′sjh為隱含層至輸出層的連接權值;其中s為并列子網絡的序號,s=1,2,3;i為輸入層神經元序號,i=1,2;j為隱含層神經元序號,j=1,2,3;h為輸出層神經元序號,h=1。
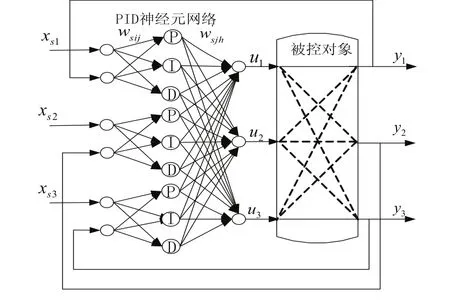
圖1 三變量PID神經網絡解耦控制系統
2.1 PID神經網絡初始權值優選方法
為改善上述提出的PID神經網絡不足,采用遺傳算法對PID神經網絡初始權值進行優選,方法如下:
1)將網絡的權值用一組十進制編碼的實數表達。任一組完整的權值相當于一條染色體(WR= (wsij,wsjh)=(w1ij,w2ij,w3ij,w1jh,w2jh,w3jh)),本系統中網絡的初始權值共有45個。這樣的染色體共有R個,即權值種群規模為R。
2)在遺傳算法中,適應度函數為進化目標,只能向適應度值增大的方向進化。在選擇運算中,適應度值較大的染色體有較大的存在機會。目標函數為在進化代中搜索網絡誤差最小的染色體。表達式如下:
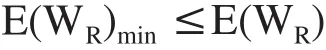
由于網絡誤差是非零正數,可將目標函數的倒數作為適應度函數。則其適應度函數為:
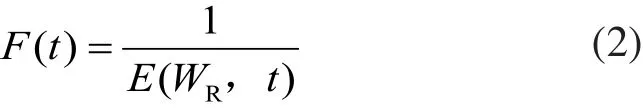
其中,E(WR,t)為第t個進化代染色體WR所具有的目標函數。
3)遺傳算法
選擇運算中,本研究采用基于適應度比例的選擇策略,每個染色體選擇概率PR為:
PR=FR/∑FR,其中FR為種群中第R個染色體的適應值。
交叉運算中,本研究采用實數交叉法,設2個染色體為Wkj,Wlj,即第k個染色體和第l個染色體在j位交叉運算后產生的新個體為[7]:
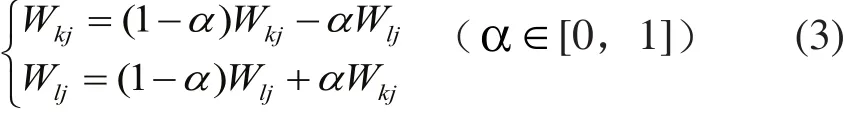
變異運算中,采用非均勻變異操作,選取Wij即第i個染色體的第j個基因進行變異[8],變異操作方法如下:
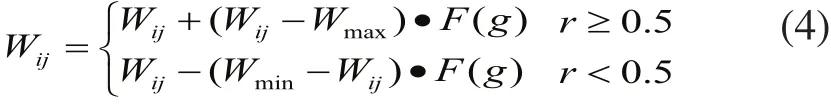
式中:Wmax、Wmin為染色體Wij的上下界;F(g)=r(1-g/Gmax),r為[0,1]間的隨機數;g為當前迭代次數;Gmax是最大進化次數。
為了保證算法的收斂性和收斂速度,同時防止出現早熟現象,對遺傳算法進行了改進。引入移民,在進化過程中利用種群的標準均方差來衡量群體的早熟程度,一旦發現種群早熟,就按一定的規則產生一定數量的高品質移民來替換種群中的劣質個體[9],早熟判斷規則如下:

式中:E(t)為第t代種群中的均方差;Wi為種群中第i個染色體;Fav為當前種群中的平均適應度。
通過遺傳算法選出最優的一組初始權值,賦值給網絡初始權值,然后PID神經網絡通過對權值的不斷修正,使系統的輸出跟隨給定值變化。
2.2 PID神經網絡權值的修正
在控制的過程中,PID神經網絡根據控制量誤差按照梯度修正法修正權值,使控制量不斷接近控制目標值,權值修正的過程如下。
目標函數:
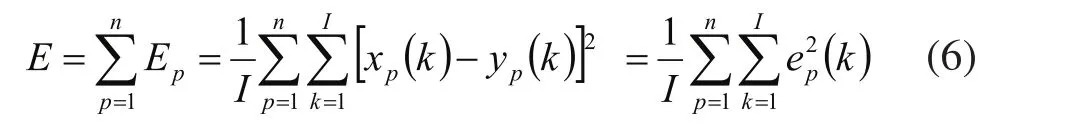
式中:I為每批采樣點數,I=100;n為被控變量個數,n=3;xp為期望輸出;yp為系統實際輸出。
按照梯度下降法調節PID神經網絡權值,經k步訓練和學習后的權值分別由以下各式確定[10]。
1)隱含層至輸出層的權值修正公式:
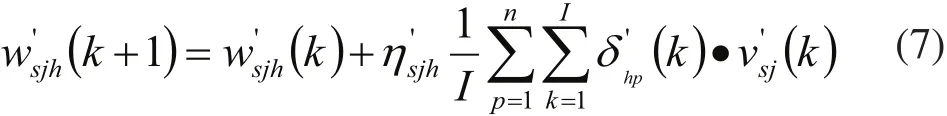
2)輸入層至隱含層的權值修正公式:
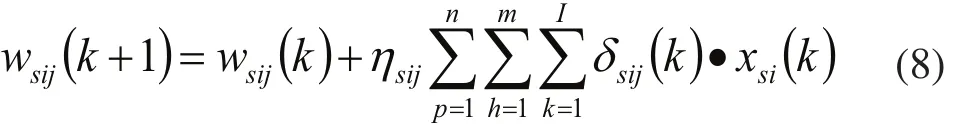
式中:xsi為輸入層神經元的輸入值; v’sj為隱含層神經元的輸出值;
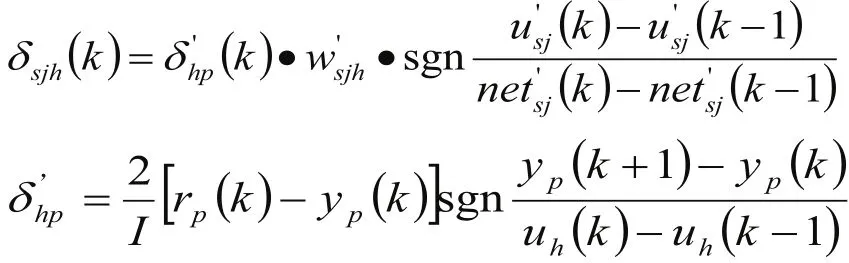
為提高網絡學習效率,在式(8)基礎上增加了動量項,增加動量項后,隱含層到輸出層權值算法和輸入層到隱含層權值算法如下:
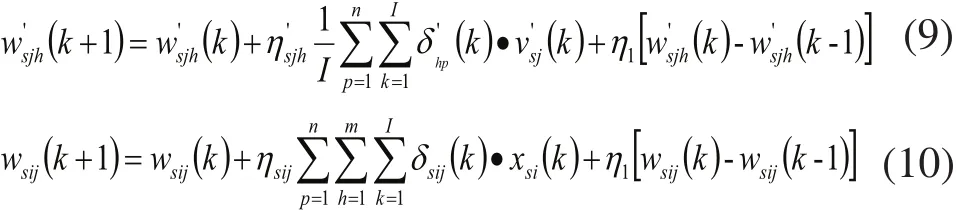
在PID神經網絡加入動量項后,可以有效的調節網絡的收斂速度,起到緩沖與平滑的作用。
3 仿真研究
為驗證上述遺傳算法優化后的PID神經網絡控制器對復雜耦合系統的解耦控制效果,本文使用Matlab軟件對式(1)所示的3輸入、3輸出多變量、非線性、強耦合系統進行仿真。
3.1 優化PID神經網絡初始權值
遺傳算法中迭代數最大為截止條件。通過上述優選方法的介紹,遺傳算法優化初始權值流程如圖2所示。
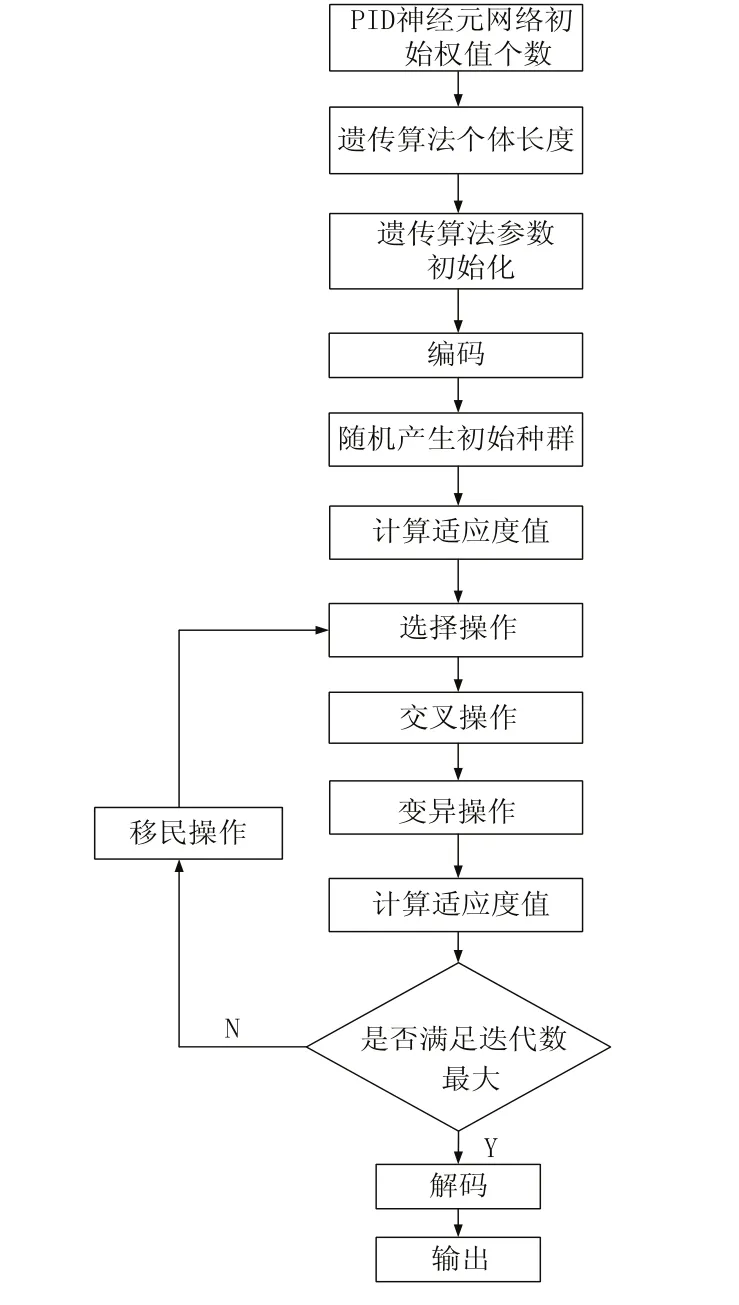
圖2 遺傳算法優化初始權值流程圖
按照流程圖編寫遺傳算法優化初始權值的Matlab程序,通過遺傳算法優化后的初始權值為W=[0.0122,-0.0685,1.0469,0.1986, 0.5529,0.1452,…,-2.0976,0.1492,0.2108],把遺傳算法優化得到的最優個體W賦值給PID神經元網絡初始權值。設置網絡權值學習速度為0.005,控制間隔時間為0.001秒,PID神經網絡的權值修正采用增加動量項的權值修正算法如式(9)、式(10)。
3.2 PID神經網絡控制系統響應效果
系統給定輸入X為階躍信號,即:
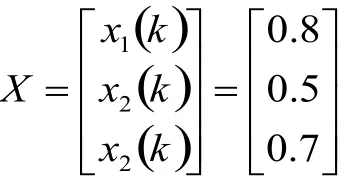
遺傳算法優化前后的PID神經網絡解耦控制系統對應輸出響應如圖3和圖4所示。
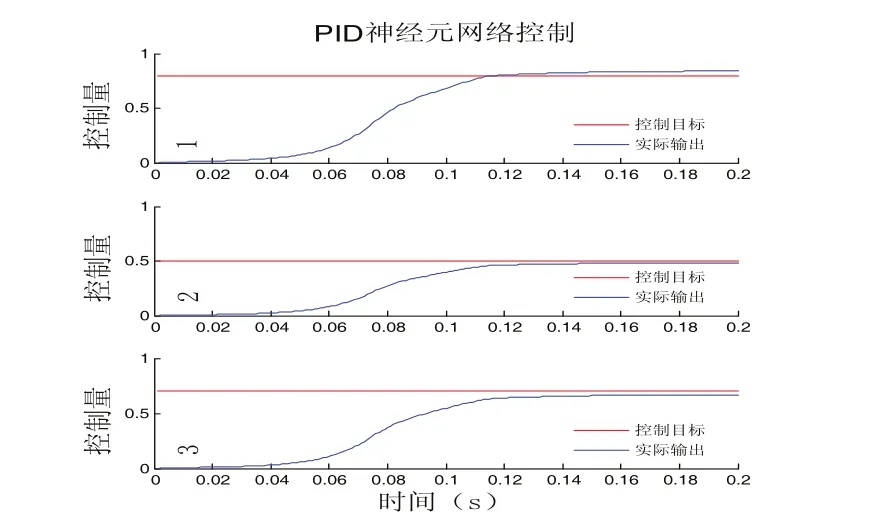
圖3 初始權值隨機選取的PID神經網絡控制器控制效果
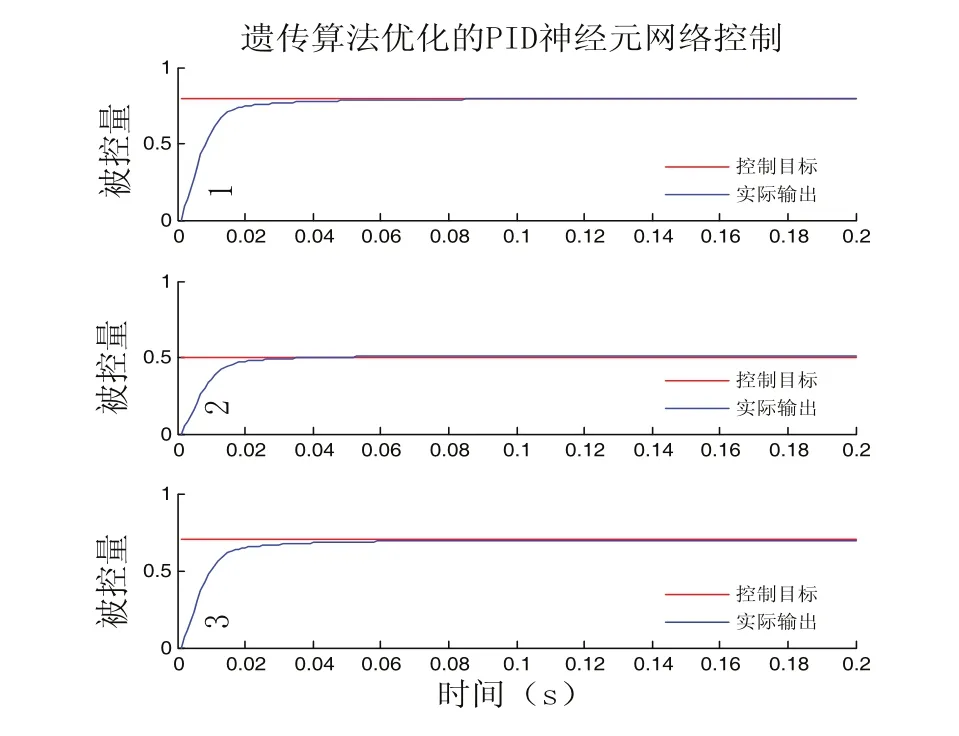
圖4 遺傳算法優化的PID神經網絡控制效果
網絡目標函數(系統誤差均方值)動態曲線如圖5和圖6所示。
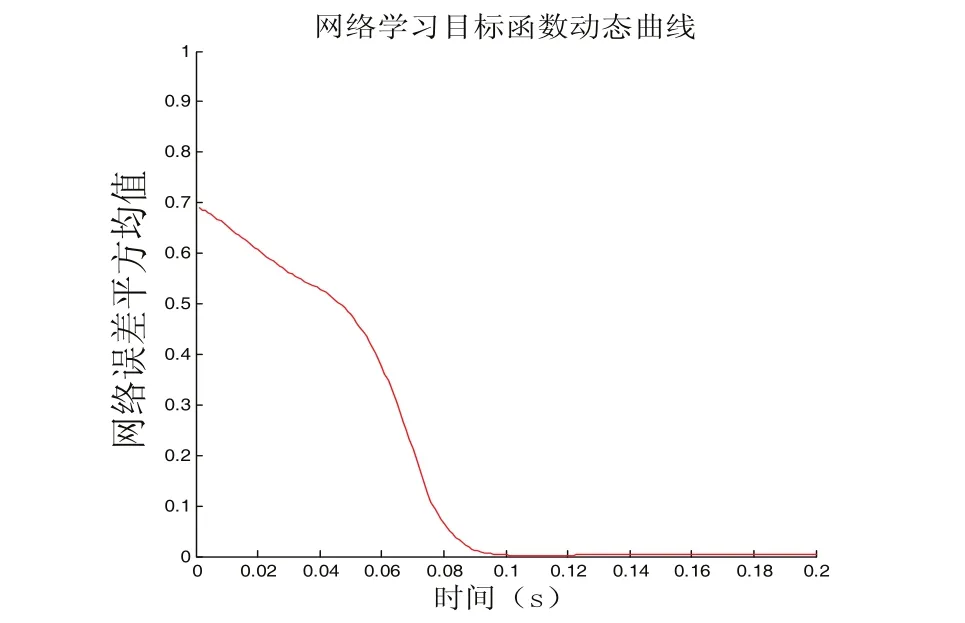
圖5 優化前網絡目標函數曲線

圖6 優化后網絡目標函數曲線
響應效果分析:
1)從圖3、4可知,優化前后,系統的超調量都非常小。
2)圖3中顯示,PID神經網絡控制器能夠控制多輸入、多輸出復雜耦合系統,系統的實際輸出跟隨控制目標變化,調節時間為0.12s。
3)圖4說明優化后的PID神經網絡能夠使系統保持較高的穩態精度和較快的響應速度,調節時間為0.02s。
4)分析圖5和圖6,優化前后網絡誤差平方均值分別在0.09s、0.025s的時候接近0,說明優化后的PID神經網絡系統控制效果更佳,調節時間更短,具有更好的自學習、自適應和解耦能力。
4 結論
1)在工業生產過程中,對復雜耦合系統的控制,傳統PID控制難以達到控制要求。文中構建的PID神經元網絡基本消除了對象之間的耦合作用。
2)遺傳算法優化后的PID神經網絡系統響應速度更快,控制精度更高。
3)基于遺傳算法的PID神經網絡解耦控制,完全可以不依賴于對象模型,通過網絡的訓練和學習實現多變量、非線性、強耦合系統的解耦。
[1]劉金琨.先進PID控制及其MATLAB仿真 [M].北京:電子工業出版社,2003:1-4.
[2]舒懷林.PID神經元網絡對強耦合帶時延多變量系統的解耦控制[J].控制理論與應用,1998,15(6):920-924.
[3]廖芳芳,肖建.基于BP神經網絡PID參數自整定的研究[J].系統仿真學報,2005,17(7):1711 -1713.
[4]黃劍平.基于BP神經網絡的PID控制研究[J].計算機仿真,2010,27(7):167-170.
[5]袁朝輝,張慧.多溫區電加熱爐的PID神經網絡控制[J].計算機仿真,2010,27(12):176-180.
[6]舒懷林,李柱.基于PID神經元多層網絡的多變量解耦控制系統[J].自動化儀表.1998,19(3):24-27.
[7]李敏強.遺傳算法的基本理論與應用[M].北京:科學出版社.2004.
[8]李敏遠,都延麗.基于遺傳算法學習的復合神經網絡自適應溫度控制系統[J].控制理論與應用,2004,21(2):242-246.
[9]歐陽森,王建華.一種新的改進遺傳算法及其應用[J].系統仿真學報.2003,15(8):1066-1068.
[10]舒懷林.PID神經元網絡及其控制系統[M].北京:國防工業出版社.2006.

