保序壓縮變換半群的理想的極大子半群

高榮海, 喻秉鈞

(1.貴州師范大學學報編輯部,貴州貴陽550001； 2.貴州師范大學數學與計算機科學學院,貴州貴陽550001；3.四川師范大學數學與軟件科學學院,四川成都610066； 4.四川師范大學文理學院,四川成都610101)

1 預備知識

1970年,B.M.Schein[1]提出了刻畫全變換半群的極大逆子半群的結構和分類的公開問題.40年來,國內外許多學者做了大量工作,不但解決了B.M.Schein提出的問題,而且創造性地提出了刻畫多種類型有限變換半群中各型極大子結構的許多方法[2-29],取得了豐碩的成果.

記Xn={1＜2＜…＜n}(n∈N+)為n元鏈.已知Xn到自身的所有變換在變換合成下成為一正則半群,記為Tn.稱α∈Tn為保序的,若?x,y∈Xn,x＜y?xα≤yα；稱α∈Tn為壓縮的,若?x,y∈Xn,|xα-yα|≤|x-y|.易知,Xn上所有保序變換之集On是Tn的一子半群；而Xn上所有退化保序壓縮變換之集Wn是On的子半群,且Wn有以下n-1個理想

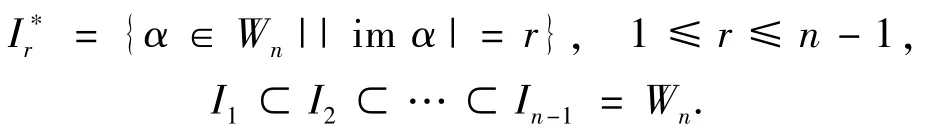
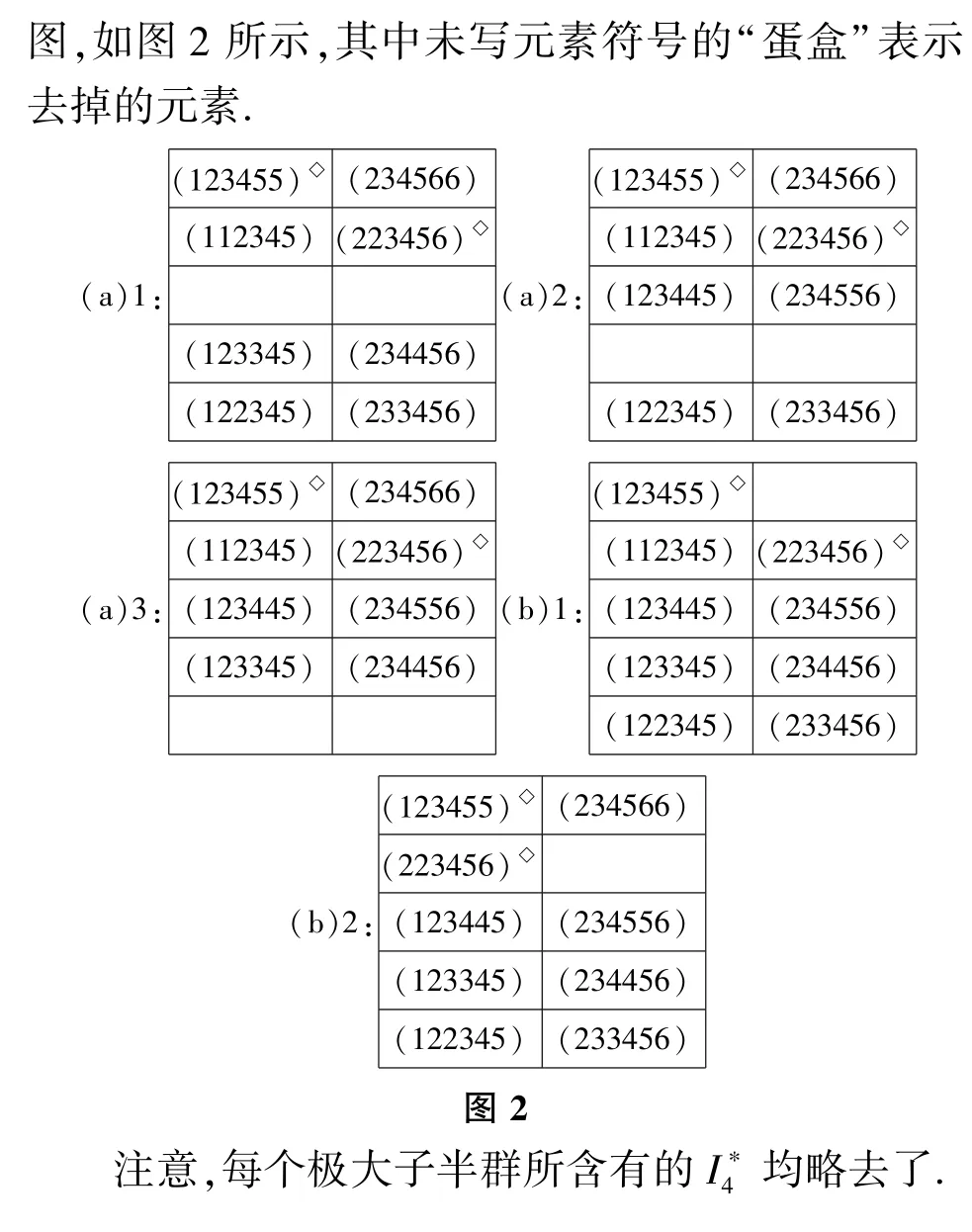
關于On和Wn的結構和性質[10-17]已有多人研究過.在本文中進一步研究Wn的理想(1≤r≤n-1)的極大子半群的結構、分類及個數.本文所用半群理論的概念和記號都是標準的,如正則元、冪等元、非正則元,Green-關系、Green*-關系等,可參看文獻[30-31],本文不再詳述.以下關于全變換半群Tn中元素的構成要素在本文中起著關鍵作用,需要特別提出.

2 主要結果及證明

[1]Schein B M.Research problems[J].Semigroup Forum,1970,1:91-92.

[2]Reilly N R.Maximal inverse semigroups ofTX[J].Semigroup Forum,1978,15:319-326.

[3]Yang X L.A classification of maximal inverse subsemigroups of finite symmetric inverse semigroups[J].Commun Algebra,1999,27(8):4089-4096.

[4]Yang X L,Lu C H.Maximal properties of some subsemigroups in finite order-preserving transformation semigroups[J].Commun Algebra,2000,28(6):3125-3135.

[5]You T J,Yang X L.A classification of the maximal idempotent-generated subsemigroups of finite singular semigroups[J].Semigroup Forum,2002,64:236-242.

[6]You T J.Maximal regular subsemigroups of certain semigroups of transformations[J].Semigroup Forum,2002,64:391-396.

[7]Xu B,Zhao P,Li J Y.Locally maximal idempotent-generated subsemigroups of singular order-preserving transformation semigroups[J].Semigroup Forum,2006,72:488-492.

[8]Zhao P,Xu B.Locally maximal idempotent-generated subsemigroups of singular orientation-preserving transformation semigroups[J].Semigroup Forum,2008,77(2):355-362.

[9]Zhao P.Maximal regular subsemiband of SOPn[J].Semigroup Forum,2010,80(2):284-291.

[10]徐波.關于有限保序部分:變換半群的極大逆子半群[J].貴州師范大學學報:自然科學版,2007,26(1):72-73.

[11]徐波,馮榮權.POn的局部極大冪等元生成子半群[J].數學的實踐與認識,2012,42(4):200-203.

[12]高榮海,徐波.OIn的理想K(n,r)的極大逆子半群[J].數學的實踐與認識,2008,38(11):154-157.

[13]徐波,趙平,李俊揚.有限部分保序變換半群POn的具有某種性質的極大子半群[J].數學雜志,2010,39(4):617-621.

[14]高榮海.具有穩定子集的有限奇異變換半群的冪等生成元[J].四川師范大學學報:自然科學版,2010,33(6):778-783.

[15]高榮海,游泰杰.半群POn的理想的極大正則子半群[J].西南大學學報:自然科學版,2011,36(5):8-11.

[16]徐波,馮榮權,高榮海.一類變換半群的秩[J].數學的實踐與認識,2010,40(8):222-224.

[17]高榮海,徐波.關于保序壓縮奇異變換半群的秩[J].山東大學學報:理學版,2011,46(6):4-7.

[18]楊浩波.全變換半群的極大逆子半群的兩個注記[J].數學雜志,2004,24(2):375-380.

[19]游泰杰.奇異變換半群的局部極大冪等元生成子半群的結構[J].貴州師范大學學報:自然科學版,2000,18(4):64-69.

[20]高榮海,游泰杰.半群PODn的理想的極大正則子半群[J].西南師范大學學報:自然科學版,2011,36(5):8-11.

[21]趙平,游泰杰,徐波.方向保序變換半群K(n,r)的極大正則子半群[J].吉林大學學報:理學版,2011,49(2):203-206.

[22]趙平,胡華碧,徐波.方向保序或反方向保序變換半群I(n,r)的極大正則子半群[J].山東大學學報:理學版,2011,46(12):60-65.

[23]Todorov K,Kracolova L.On the maximal subsemigroup of the ideals of finite symmetric semigroup[J].Simon Stevin,1985,59(2):129-140.

[24]Hotzel E.Maximal properties some semigroups of Bear Levi semigroups[J].Semigroup Froum,1995,51:153-193.

[25]Levi I,Wood G R.On maximal subsemigroups of Bear Levi semigroups[J].Semigroup Froum,1984:30:99-102.

[26]Yang X L.Maximal subsemigroups of the finite singular transformation semigroup[J].Commun Algebra,2001,39(2):1175-1182.

[27]Zhao P,Xu B,Mei Y.Locally maximal idempotent-generated subsemigroups of singular Orientation-preserving transformation semigroups[J].Semigroup Froum,2008,77(2):187-195.

[28]Zhao P.A classification of maximal idempotent-generated subsemigroups of singular Orientation-preserving transformation semigroups[J].Semigroup Froum,2008,79(2):377-384.

[29]Zhao P.Maximal regular subsemibands of SOPn[J].Semigroup Froum,2010,80(3):477-483.

[30]Howie J M.Fundamentals of Semigroup Theory[M].Oxford:Clarendon Press,1995.

[31]Fountain J B.Abundant semigroups[J].London Math Soc,1982,44(3):103-129.